基于宽频阻抗谱技术的XLPE电缆老化诊断方法研究

单秉亮，李舒宁，孙茂伦，杜承谦，王 伟，李成榕，孟晓凯

（1.新能源电力系统国家重点实验室（华北电力大学），北京 102206；2.国网山西省电力公司电力科学研究院，山西 太原 030001）

0 引言

交联聚乙烯（XLPE）电力电缆以其良好的绝缘性能和耐热性能，广泛应用于我国城市电网的建设与改造。作为城市电能传输和分配的主要设备，其运行状况及可靠性直接关系到整个电网系统的安全与稳定。截至目前，我国XLPE电缆大规模入地接近20年，已逐步进入“老龄化”阶段，部分在役电缆正接近或已超过其设计寿命，由此带来的电缆本体绝缘老化问题正日益威胁着电网的运行安全[1]。因此，及时、准确掌握电缆本体绝缘老化状态，并据此开展合理的状态检修显得愈发重要[2-3]。

目前研究相对成熟且可用于现场电缆老化诊断的技术相对较少，主要以取样分析技术和0.1 Hz超低频介损检测技术为代表[4]。前者可用于评估电缆发生的热老化、水树老化等，后者则更倾向于诊断电缆中的水树老化[5-7]。然而，取样分析技术在现场应用时具有破坏性，仅适用于取样成本相对较低、整体近似呈均匀老化配电电缆的老化诊断[5-6]；0.1 Hz超低频介损检测技术虽然已被列为电缆现场试验内容之一，但其能否与工频介损检测完全等效并反映工频下运行电缆的绝缘状态仍需进一步研究，且施加的高达1.5U0的0.1 Hz超低频电压也有可能激发电缆中潜在的绝缘缺陷并造成二次伤害[7]。在此情况下，探索新型电缆老化诊断方法，有利于加快解决我国存在的大规模电缆老化问题，相关研究工作刻不容缓。

近年来，以宽频阻抗谱（broadband impedance spectroscopy，BIS）[8-10]和反射系数谱（reflection coefficient spectroscopy，RCS）[11]为代表的频域反射（frequency domain reflectometry，FDR）技术被国内外学者用于研究电力电缆中的缺陷定位。相较传统时域反射（time domain reflectometry，TDR）技术而言，FDR技术的测量信号中含有更多的高频成分，对于电缆电气参数变化较小的本体老化缺陷也具有较高灵敏度[12]。然而，现有研究中该技术主要用于电缆中的缺陷定位，基于其诊断电缆本体绝缘老化的研究相对较少。

鉴于此，本文深入研究BIS技术，提出利用电缆输入阻抗谱计算电缆中波速并据此诊断XLPE电缆绝缘老化的方法，并通过仿真和试验研究论证该诊断方法的有效性。

1 电缆波速诊断绝缘老化的依据及其计算方法

1.1 诊断依据

以图1所示的单芯10 kV XLPE电缆为例，分析电缆老化对高频电磁波在电缆中传播速度的影响。

由图1可知，XLPE电缆绝缘结构主要由XLPE绝缘层和内、外半导电层共同构成，因此电缆绝缘结构等效电容Cequal可按式（1）计算。

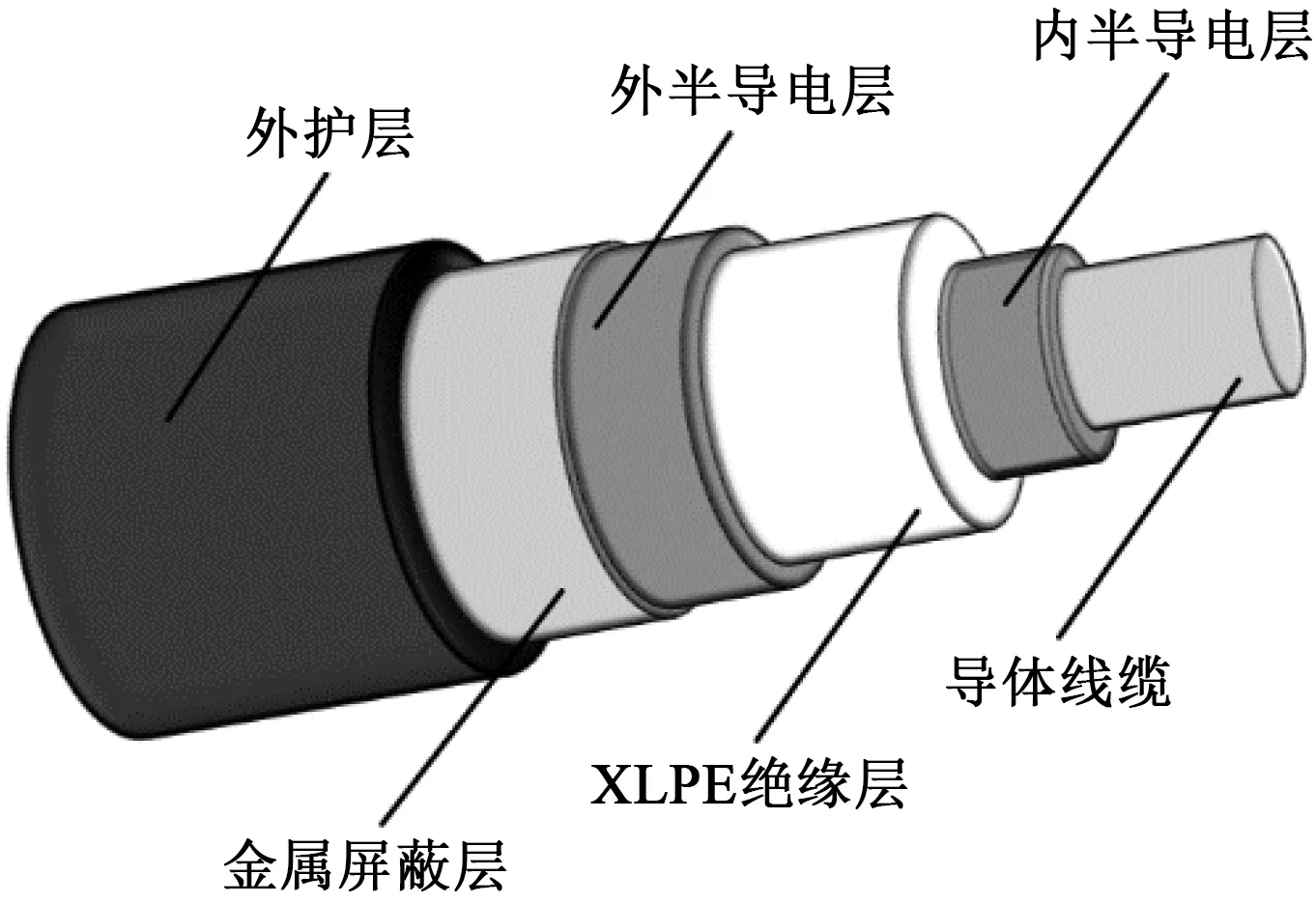
图1 XLPE电缆结构示意图Fig.1 Structure diagram of XLPE cables

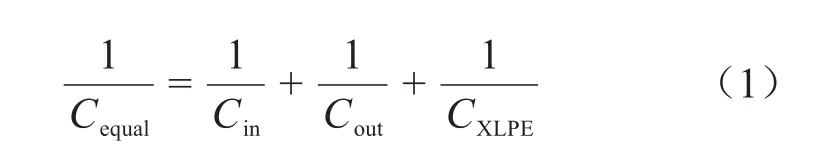
式（1）中：CXLPE表示电缆XLPE层的电容值；Cin、Cout分别表示电缆内、外半导电层的电容值。XLPE电缆在实际运行过程中，其绝缘层会在电、热、机械、环境等因素作用下发生老化，进而影响电缆绝缘结构的介电特性。

水树老化和热老化是运行电缆绝缘主要的老化形式，电缆发生水树老化时，其XLPE绝缘层中的内部极性基团及空间电荷数量会明显增多，相应的松弛极化过程也会显著增强；电缆发生热老化时，XLPE分子链会发生断裂继而形成低分子产物，这在一定程度上可以加剧界面极化，上述过程均会引起XLPE绝缘层相对介电常数的增大[13-14]。与此同时，由于材料电容值和其相对介电常数正相关，XLPE绝缘层电容值也会随之变大。假设电缆老化过程中其内外半导电层的相对介电常数（或电容）基本保持不变，则根据式（1）可知，老化电缆XLPE绝缘层电容值的提高会导致绝缘结构整体等效电容Cequal的增大，这在一定程度上意味着电缆绝缘结构整体等效相对介电常数也随之增大。而对于XLPE电缆而言，高频电磁波在其内部的传播速度v与频率基本无关，可表示为式（2）[15]。

式（2）中：c0为电磁波在真空中的波速；εr和μr分别表示介质的相对介电常数和相对磁导率。

鉴于前文已阐述电缆老化后其整体等效相对介电常数会有所提高，结合式（2）可以看出，等效相对介电常数的提高最终会导致波速v降低。因此，电缆老化会导致波速v发生改变，可据此开展电缆老化诊断工作。

1.2 基于输入阻抗谱的电缆波速计算方法

长度为l的电缆末端开路时的输入阻抗幅值频谱Z|in|可表示为式（3）[16]。

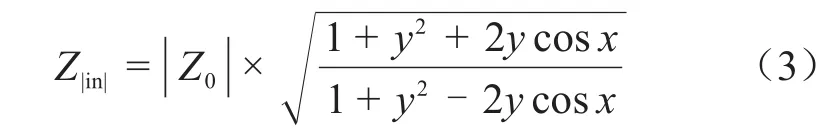
式（3）中：Z0为电缆的特征阻抗；x=-2βl，y=e-2αl，其中α和β分别为电缆的衰减系数和相位系数。鉴于高频下电缆Z0取值近似为常数[17]、y恒为正值，当且仅当cosx=1时，Z|in|会取极大值。此时，x=-2βl=2kπ，其中k为整数。

与此同时，β可表示为式（4）。

式（4）中：f为信号的频率；ν为电缆中波速。因此电缆输入阻抗幅值的极大值出现的频率为式（5）。

设fn+1和fn分别为电缆输入阻抗幅值第（n+1）和第n个极大值所对应的频率，n为非负整数。则电缆波速ν可表示为式（6）。

需说明的是，对于均匀老化电缆而言，式（6）求得的波速ν代表电缆中任意位置的波速；对于分段老化电缆而言，根据式（6）计算的波速实际上为电缆中的平均波速[18]。

2 仿真研究

2.1 仿真参数

文献[16,19]对10 kV XLPE电缆绝缘结构（包括XLPE绝缘层及内、外半导电层）在不同热老化情况下的频域介电响应特性进行了测量。鉴于在103～109Hz频率范围内XLPE的极化过程主要以偶极子的转向极化为主[20]，文献[16]基于Cole-Cole模型利用式（7）来拟合10 kHz～100 MHz内XLPE电缆绝缘结构的复介电常数变化过程。

式（7）中：ε′和ε″分别为介质介电常数的实部和虚部；C、D和P为拟合系数；ε0为真空的介电常数；ω为角频率。拟合后不同热老化程度下XLPE电缆绝缘复介电常数拟合参数值如表1[16]所示。本研究在仿真过程中，通过改变电缆不同位置绝缘复介电常数拟合参数值即可模拟不同老化程度及老化区域分布的电缆。此外，仿真过程中电缆金属导体半径为10 mm，电缆绝缘厚度为5.5 mm，金属屏蔽层厚度为0.2 mm。

表1 不同热老化电缆绝缘复介电常数拟合参数值Tab.1 Fitting parameters of complex dielectric constants of different thermal ageing cable insulations

2.2 电缆均匀老化诊断仿真研究

2.2.1 老化程度对波速的影响

以100 m长的单芯10 kV XLPE电缆为例，仿真电缆在整体未老化、均匀轻微老化和均匀严重老化3种情况下末端开路时的输入阻抗幅值频谱，结果如图2所示。从图2可以看出，不同老化程度电缆的输入阻抗幅值频谱存在明显差异，电缆老化越严重，其阻抗幅值频谱相邻极大值对应的频率间隔越小。

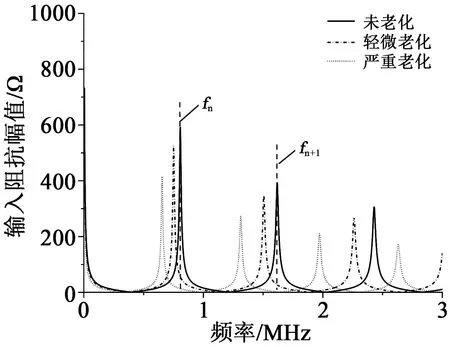
图2 不同程度均匀老化电缆的输入阻抗幅值频谱Fig.2 Input impedance amplitude spectra of uniform ageing cables with different ageing degrees

结合式（6）计算电缆各老化程度下的波速，结果对比如图3所示。从图3可以看出，整体未老化、均匀轻微老化和均匀严重老化3种情况下电缆中波速分别为162、151、132 m/μs，不同老化程度电缆的波速差异较大，电缆的老化程度与波速确实存在明显的对应关系。电缆老化越严重，对应的波速越小，例如当电缆发生严重老化时，其波速相较未老化时下降了18.5%，变化幅度较为明显。上述规律与1.1中的理论依据分析相一致，因此，电缆中波速具有诊断均匀老化电缆老化状况的潜力。

图3 均匀老化电缆波速和老化程度的关系Fig.3 Correlation between wave velocity and ageing degree of uniform ageing cables

2.2.2 电缆长度对波速的影响

实际运行电缆长度不一，为研究基于输入阻抗谱计算不同长度电缆中波速的稳定性，本研究进一步仿真了10 m、1 000 m两种长度电缆在整体发生均匀老化和未老化时的阻抗幅值频谱，分别计算电缆中波速并与图3中100 m电缆波速进行对比，结果如图4所示。由图4可以看出，当电缆老化状态相同时，不同长度电缆中波速的计算值差异较小。这在一定程度上证明了基于电缆输入阻抗谱计算电缆中波速的稳定性较好，基本不受长度的影响。

图4 不同长度电缆中波速计算值Fig.4 Calculated values of wave velocity in cables with different lengths

2.3 电缆分段老化诊断仿真研究

由于XLPE配电电缆空间跨度大、敷设环境复杂，运行电缆分段老化现象普遍存在，如图5所示，即电缆绝缘老化状态沿其线路并非呈均匀分布，亟需研究电缆波速对电缆分段老化诊断的有效性。

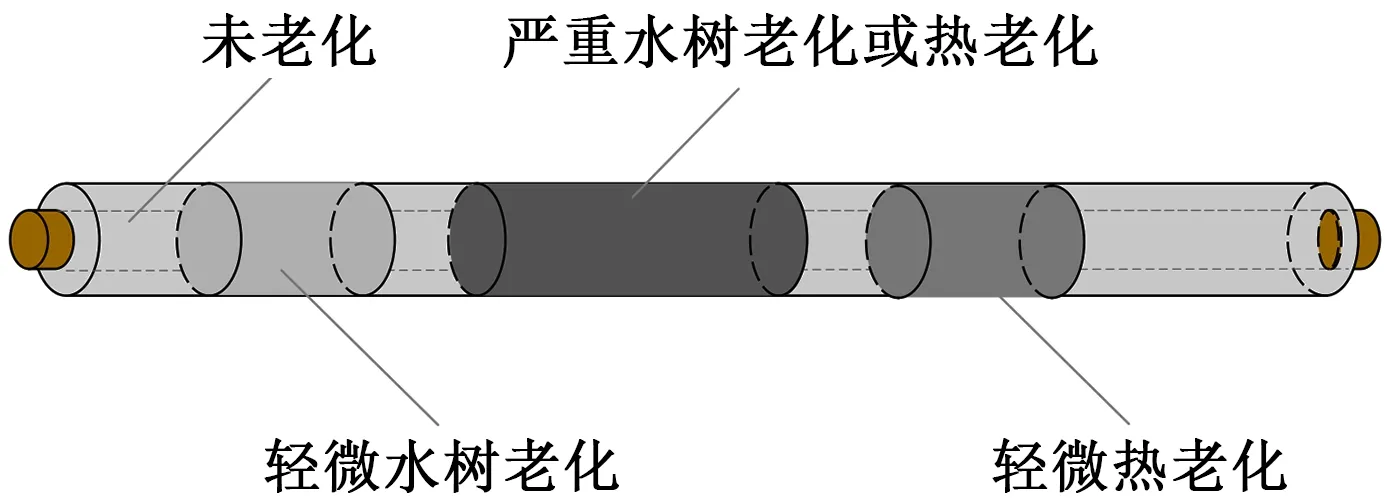
图5 分段老化电缆示意图Fig.5 Structure diagram of the segmented-ageing cable

2.3.1 电缆分段老化程度对平均波速的影响

首先以100 m长的单芯10 kV XLPE电缆为例，将距电缆首端20～60 m的区域设为分段老化发生位置，其他区域设为未老化区域。在电缆末端开路的条件下仿真了分段老化区域发生均匀轻微老化和均匀严重老化两种情况下的首端输入阻抗幅值频谱，并与100 m未老化电缆的仿真结果进行对比，结果如图6所示。从图6可以看出，电缆发生分段老化时，其输入阻抗幅值频谱同样与未老化电缆存在明显差异。结合式（6）计算各电缆的平均波速如图7所示。

图6 不同程度分段老化电缆的输入阻抗幅值频谱Fig.6 Input impedance amplitude spectra of segmentedageing cables with different ageing degrees

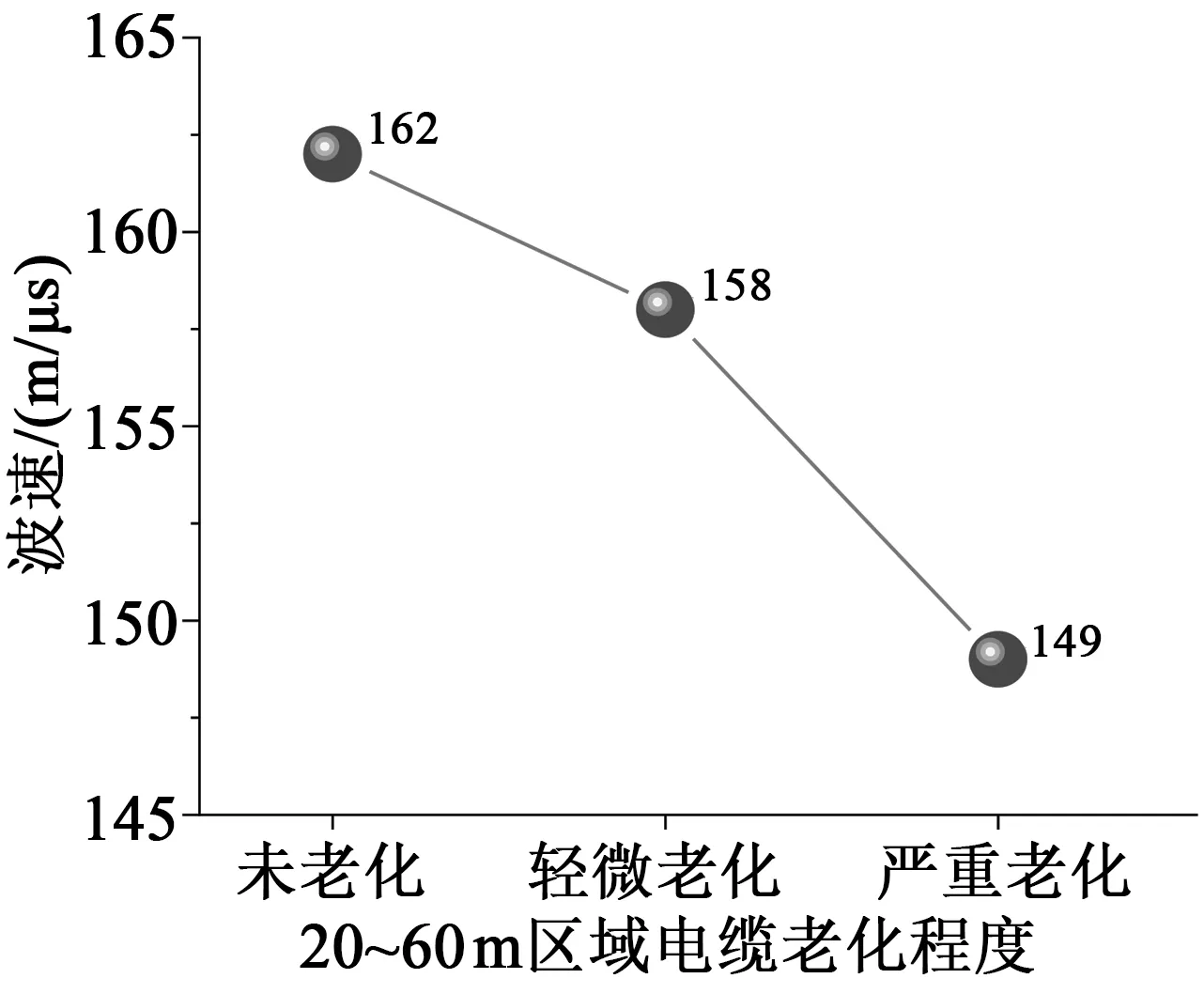
图7 分段老化电缆平均波速和老化程度的关系Fig.7 Correlation between average wave velocity and ageing degree of segmented-ageing cables

从图7可以看出，随着电缆分段老化严重程度的增加，电缆平均波速逐渐减小。由此可见，基于输入阻抗谱计算得到的平均波速可以有效地反映出电缆分段老化严重程度的变化。

2.3.2 电缆分段老化区域长度占比对平均波速的影响

在上述研究基础上，进一步仿真研究了电缆分段老化区域不同长度占比情况下的输入阻抗幅值频谱，结合式（6）计算了电缆平均波速与电缆分段老化区域长度占比的关联关系，结果如表2所示。其中，电缆分段老化发生位置区域（距电缆首端）分别为：20～21 m、20～25 m、20～30 m、20～40 m、20～60 m、20～80 m、20～100 m、0～100 m，即电缆分段老化区域占比分别为1%、5%、10%、20%、40%、60%、80%、100%。

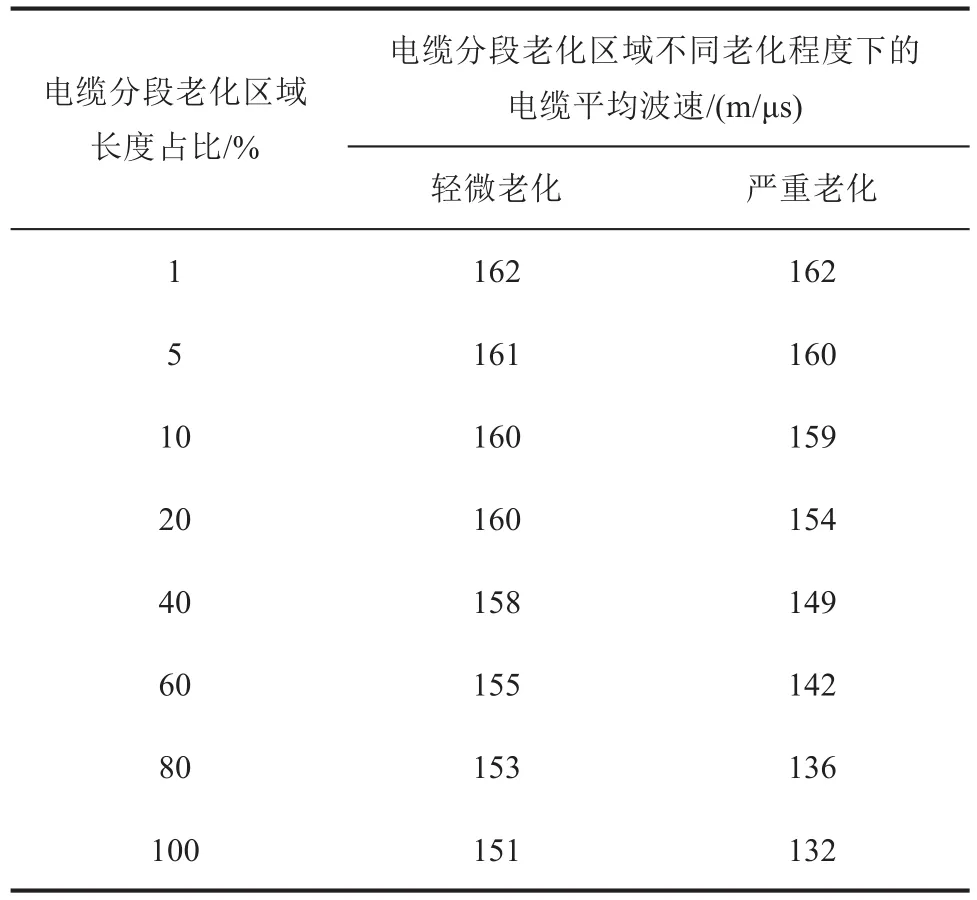
表2 分段老化电缆平均波速和老化区域长度占比的关系Tab.2 Correlation between average wave velocity and length percentage of ageing areas of segmented-ageing cables

从表2可以看出，当电缆分段老化区域老化程度相同时，分段区域长度占比越高，对应的电缆平均波速越小。当电缆分段老化区域长度占比相同时，分段老化区域老化越严重，电缆平均波速同样越小。因此，基于电缆平均波速可以有效地表征电缆分段老化区域长度占比的变化。此外，可以发现，当电缆分段老化区域长度占比为1%时，电缆平均波速相较未老化电缆波速基本一致；而当电缆分段老化区域长度占比大5%时，电缆平均波速发生改变，此时电缆老化可以被有效诊断。

2.3.3 电缆分段老化发生位置对平均波速的影响

由于电缆绝缘老化过程受敷设环境因素影响较大，电缆分段老化发生位置并非固定。但在评价电缆绝缘老化状态时所选取的表征量不应受电缆分段老化发生位置的影响。同样以100 m长的单芯10 kV XLPE电缆为例，仿真电缆分段老化总长度同为40 m，分段老化程度及发生位置不同时的电缆输入阻抗谱，并据此计算各老化情况下的电缆平均波速结果如图8所示。其中，电缆分段老化发生位置区域如下：①距电缆首端10～30 m和50～70 m；②距电缆首端20～60 m；③距电缆首端30～70 m；④距电缆首端40～80 m；⑤距电缆首端20～40 m和60～80 m。从图8可以看出，当电缆分段老化长度占比相同时，电缆平均波速只与电缆分段老化严重程度相关，基本不受电缆分段老化发生位置的影响。

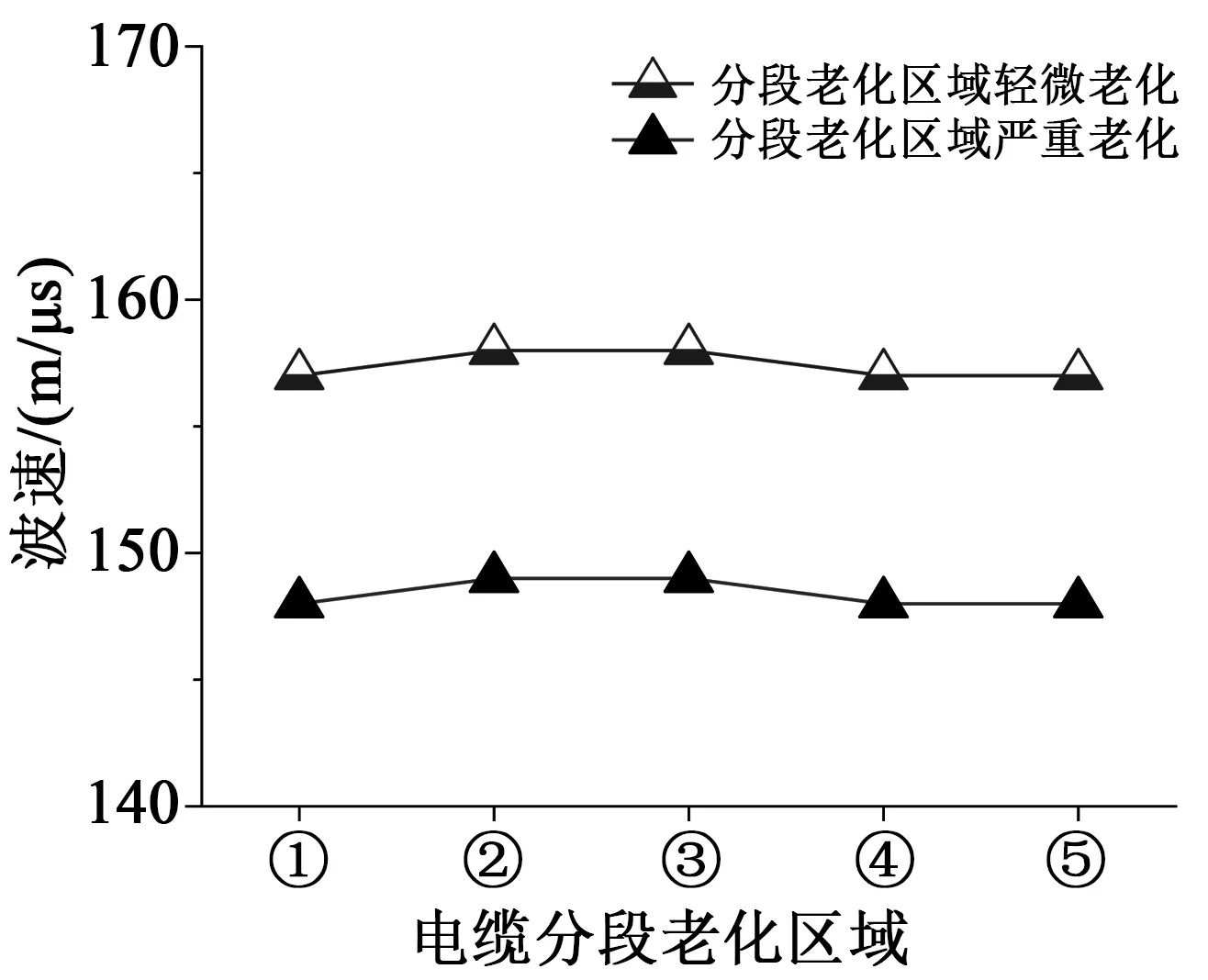
图8 分段老化电缆平均波速和老化区域位置分布的关系Fig.8 Correlation between average wave velocity and distribution of ageing areas of segmented-ageing cables

基于上述仿真研究可以看出，对于均匀老化电缆而言，电缆老化越严重，电缆波速越小，且电缆波速与电缆长度无关；对于分段老化电缆而言，电缆分段老化严重程度或分段老化区域长度占比的增加同样会导致电缆中平均波速的降低，且电缆平均波速与分段老化发生位置基本无关。因此，可以基于电缆中平均波速诊断电缆整体老化状态。

3 试验研究

为验证本研究所提的电力电缆本体整体绝缘老化状态诊断方法的有效性，在实验室搭建了如图9所示的测试平台。

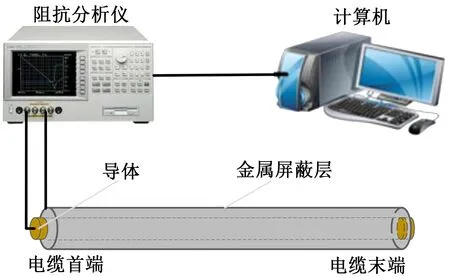
图9 电缆缺陷定位试验平台Fig.9 Test platform for defect location of the cable

首先利用Agilent 4294A型阻抗分析仪测量了长度为99 m的单芯10 kV XLPE电缆在末端开路状态下的阻抗幅值频谱，测试频谱范围为40 Hz～20 MHz，测量结果如图10所示。

图10 未老化电缆的首端输入阻抗幅值频谱Fig.10 Amplitude spectrum of input impedance at the head end of the unaged cable

随后，截取长度为3.18 m的电缆，用大电流发生器给电缆导体加热，模拟电缆实际过载运行导致的绝缘热老化，其中导体线芯温度控制在135℃，室温为25℃，老化时间为64天。老化完成后，利用阻抗分析仪测试了老化后电缆的阻抗幅值频谱。随后将此3.18 m老化电缆与同型号4.06 m未老化电缆串联构成分段老化电缆，同样对其输入阻抗幅值频谱进行测试。两次阻抗幅值频谱的测试频率范围均为40 Hz～30 MHz，测量结果如图11所示。

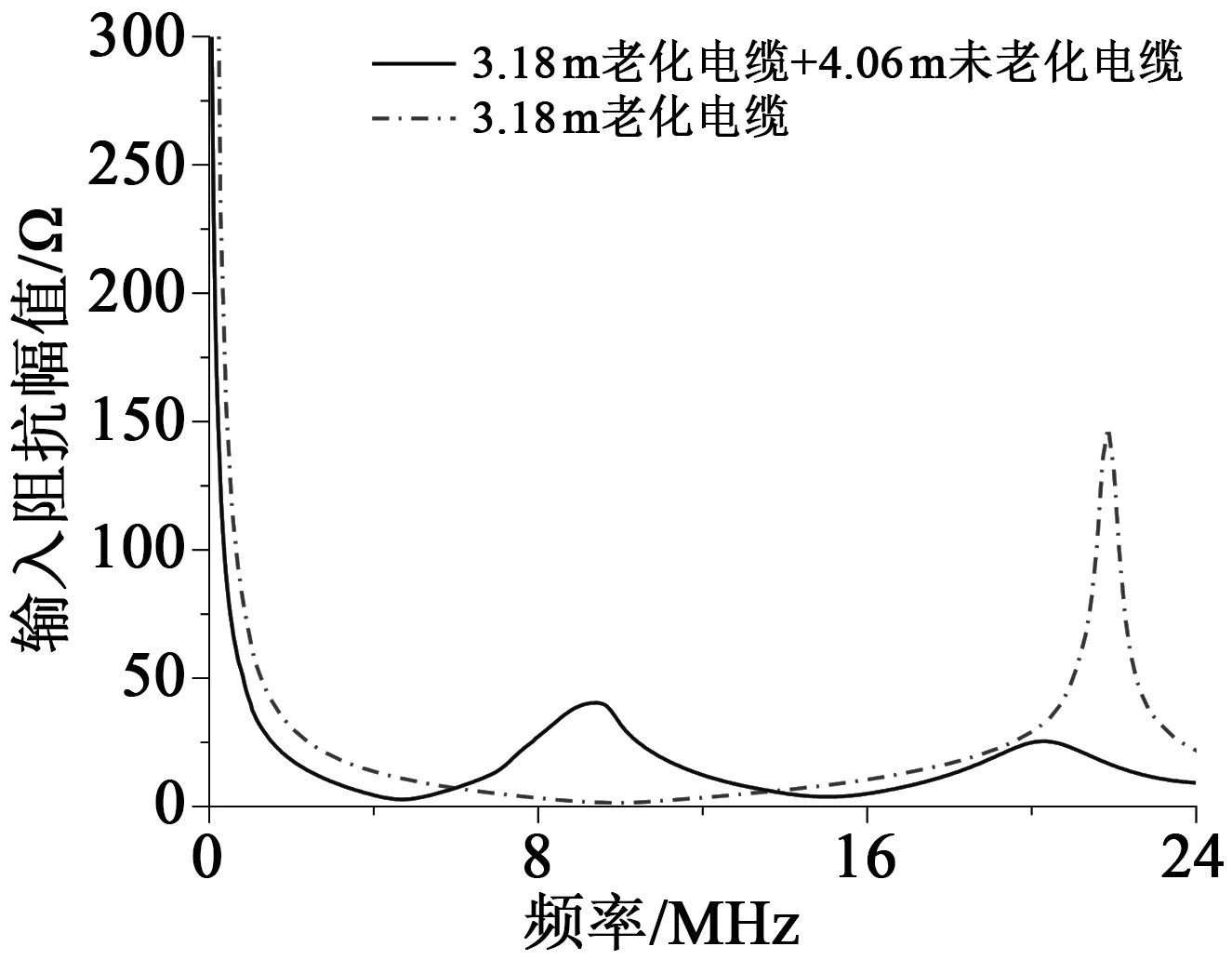
图11 热老化后电缆的输入阻抗幅值频谱Fig.11 Amplitude spectra of input impedance of the cable after thermal ageing

在此基础上，利用式（6）计算各电缆中的平均波速，得到未老化电缆、分段老化电缆以及老化电缆中平均波速值分别为166、152、139 m/μs。均匀热老化后电缆波速相较老化前降低了16.3%，降低幅度较为明显。与此同时，分段老化电缆中的平均波速高于均匀老化电缆中波速，低于未老化电缆中波速。上述试验结果表明，无论电缆发生均匀老化还是分段老化，电缆中的平均波速均会有所降低，基于电缆平均波速可有效表征均匀老化电缆和分段老化电缆的整体老化状态。

此外，王晓威[21]对上述老化前后电缆绝缘部分内、中、外3层绝缘材料的力学性能进行了测试，将本研究电缆中波速测量结果与其测试结果对比如表3所示。从表3可以看出，电缆老化后绝缘部分各层的断裂伸长率显著降低，波速在一定程度上可与断裂伸长率和波速的变化很好地对应。

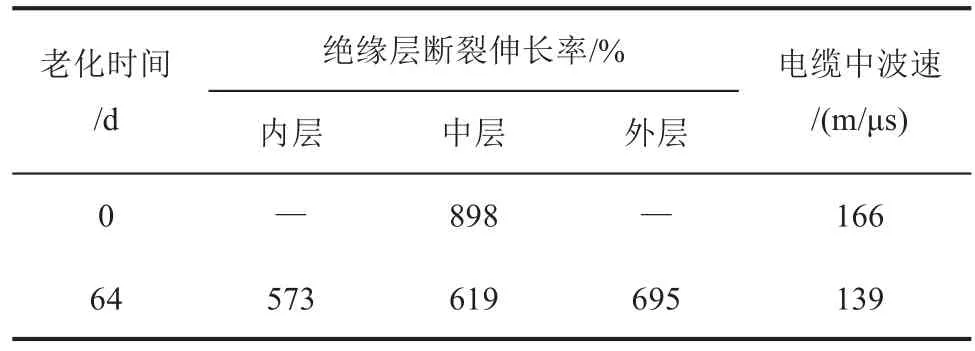
表3 电缆老化前后性能参数对比Tab.3 Comparison of performance parameters of the cable before and after ageing

4 分析与讨论

时域反射技术同样可以用于电缆中波速的测量，但测量过程中会由于时域脉冲传播过程中的波形畸变而影响波速计算结果的准确性；与此同时，当电缆长度较短时对于测试仪器性能要求较高。而本研究提出的基于输入阻抗谱的波速计算方法原理主要基于电缆线路阻抗频谱“谐振”效应，其“谐振频率”基本不受波形畸变影响，在一定程度上可以提高波速测量准确性[22]。此外，考虑仪器自身采样率对于输入阻抗幅值频谱波形完整性的影响，可利用多个谐振周期频率间隔值来计算电缆中的波速以降低误差。

5 结论

（1）电缆老化会引起绝缘结构相对介电常数的增大，导致电缆中高频电磁波传播速度的减小。本研究利用电缆输入阻抗幅值频谱计算电缆中平均波速，并据此提出基于电缆中平均波速诊断电缆整体绝缘老化状态的方法。

（2）对于均匀老化电缆而言，电缆老化越严重，电缆中波速越小，且波速与电缆长度无关；对于分段老化电缆而言，电缆分段老化严重程度或分段老化区域长度占比的增加均会导致电缆中平均波速的减小，且电缆平均波速与分段老化发生位置基本无关。

（3）基于试验研究发现电缆热老化后绝缘层的断裂伸长率和电缆中波速均有所降低，且这两种性能参数的变化趋势可以很好地对应，验证了基于波速诊断电缆绝缘老化状态的有效性。