太湖隧道明挖段恢复堤防变形特性分析
张孟颖, 吴东伟, 孙云儒, 朱家胜, 吴 健
(1.江苏省水利勘测设计研究院有限公司, 江苏 扬州 225127; 2.河海大学 水利水电学院, 江苏 南京 210098; 3.浦口区水务局, 江苏 南京 211899)
随着城镇化进程的发展及城市建设需求的加大,我国的地下交通发展迅速,产生了大量深基坑工程。深、大基础建造过程中,地基土工程行为已不再是单调加载过程,更多地包含了卸荷回弹及加载再压缩等力学过程,应力路径趋于复杂。近代土力学研究已表明,地基土的力学行为不仅取决于土体最初和最终的应力状态,而且与其应力历史和应力路径有关[1]。鉴此,本文基于工程开挖、回填工序,同时考虑基坑支护结构、隧道主体结构及初设地应力等因素,利用有限元计算软件,建立了有限元计算模型,分析了基坑开挖及堤防恢复的变形特性,以期为堤防沉降变形计算提供理论支撑。
1 工程概况
1.1 工程基本情况
太湖隧道为苏锡常南部高速公路穿越太湖梅梁湖的主要工程,同时也是江苏省“五纵九横五联”高速公路网中“横六”的重要组成。隧道与苏、锡、常3个市的高速公路环线直接沟通,实现3个市绕城高速间交通流的自由转换,隧道全长10.8 km,分别在太湖马山和南泉处穿越太湖大堤,堤防级别均为2级。太湖隧道进口马山段堤防顶高程为6.30 m(吴淞高程,下同),上设70 cm高防浪墙,堤顶为等级公路。出口南泉段堤防顶高程为7.00 m,顶宽5~6 m。隧道采用明挖破堤施工,隧道基坑采用钻孔灌注桩结合三道水平支撑体系的围护方案,三道水平支撑均采用钢管支撑[2]。
1.2 工程地质
根据工程地质勘测报告,自上而下可分为6个工程地质层。部分主要土层工程特性简介如下:
2-1(Q3)(粉质)黏土:灰黄色,可塑~硬塑状态,中偏低~低压缩性,夹铁锰结核,土质较好,全线连续稳定分布。
2-2(Q3)粉质黏土:灰黄色,灰色,软塑~可塑状态,中等压缩性,夹粉砂,断续分布。
2-3(Q3)粉土或粉砂:灰黄色,灰色,湿(饱和),稍密~中密状态,局部为粉质黏土夹粉砂,沿线局部分布。
2-4(Q3)粉质黏土:黄灰色,灰色,软塑状态,局部流塑状态,中等偏高压缩性,夹粉砂,断续分布。
3-1(Q3)(粉质)黏土:灰黄色,灰色,可塑~硬塑状态,中偏低~低压缩性,夹铁锰结核,土质良好,全线连续稳定分布。
3-2(Q3)粉质黏土:灰黄色,灰色,软塑~可塑状态,中等压缩性,夹粉砂,断续分布。
3-3(Q3)粉土,部分为粉砂:灰黄色,灰色,湿(饱和),中密~密实状态,局部分布。
4-1(Q3)(粉质)黏土:黄灰色,灰黄色,青灰色,可塑~硬塑状态,中等~低压缩性,夹铁锰结核,局部夹钙质,土质良好,全线断续分布。
2 有限元模型的建立
2.1 本构模型及土体参数的选取
有限元数值模拟计算成果能否反映工程实际,并运用到工程设计中指导工程实践,往往取决于是否采用了合理的本构模型及正确的材料参数。根据以往研究成果显示,弹性模型无法反映土体的塑性性质,而塑性模型中MC模型和DP模型由于采用单一刚度导致坑底回弹较大[3]。以上几种模型都不能很好地模拟基坑开挖、回填后变形,不适合用于本工程模拟计算。因此,本文采用可区分加卸载并能同时考虑软黏土应变硬化特征,且其刚度依赖于应力历史和应力路径的修正剑桥模型[4],该模型可给出较合理的“卸载—再压缩”土体变形情况。模型中土体及围护结构均采用四边形四节点平面应变单元CPE4,各层支撑模拟按线弹性材料考虑采用梁单元B21。各土层计算模型材料参数[5]详见表1。
2.2 计算模型及土性参数的选取
隧道基坑大体呈矩形,属于三维空间问题,尤其是角点附近的空间效应特别明显,但对标准段来讲,当工程的长宽比大于4时,在标准段中部剖面上二维和三维有限元分析的变形情况基本一致[6]。考虑到采用二维有限元计算模型单元与节点相对较少,且分析相对简单。为便于处理、节省计算时间,本文采用二维有限元分析。根据以往建模经验,本次模型深度取120m,上部取至堤顶面高程,下部取至3-1层土,计算深度超过基坑开挖深度的4倍;两边边界取至支护桩外80m,超过基坑开挖深度的3倍。在计算模型左右两侧边界施加水平方向位移约束,底面边界施加水平和竖直方向位移约束。为获得更好的计算精度,不同区域网格划分疏密有别,总体以靠近围护桩网格较密、远离围护桩方向网格逐渐稀疏为原则[4]。有限元模型及网格划分见图1。
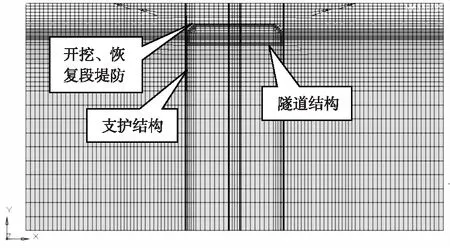
图1 有限元模型及网格划分
3 有限元分析过程
3.1 支护结构模型建立
隧道基坑支护采用排桩结构,排桩支护虽由单个桩体组成,但其受力形式类似于地下连续墙,因此在计算中将排桩墙通过等刚度转换,等价为一定厚度的连续式板桩墙进行分析计算。并可证明,按此等价的地下连续墙计算的结果合理、偏于安全[7]。则等刚度转换按式(1)计算,计算简图见图2。
(1)
式中:d为等价的地连墙厚度;R为桩的桩径;a为桩间净距,则单个桩应等价为长R+a的地连墙。
经计算,排桩可等刚度换算为厚0.90 m的连续式板桩墙,桩长按原排桩支护结构取用,即27.5 m,用于分析计算。
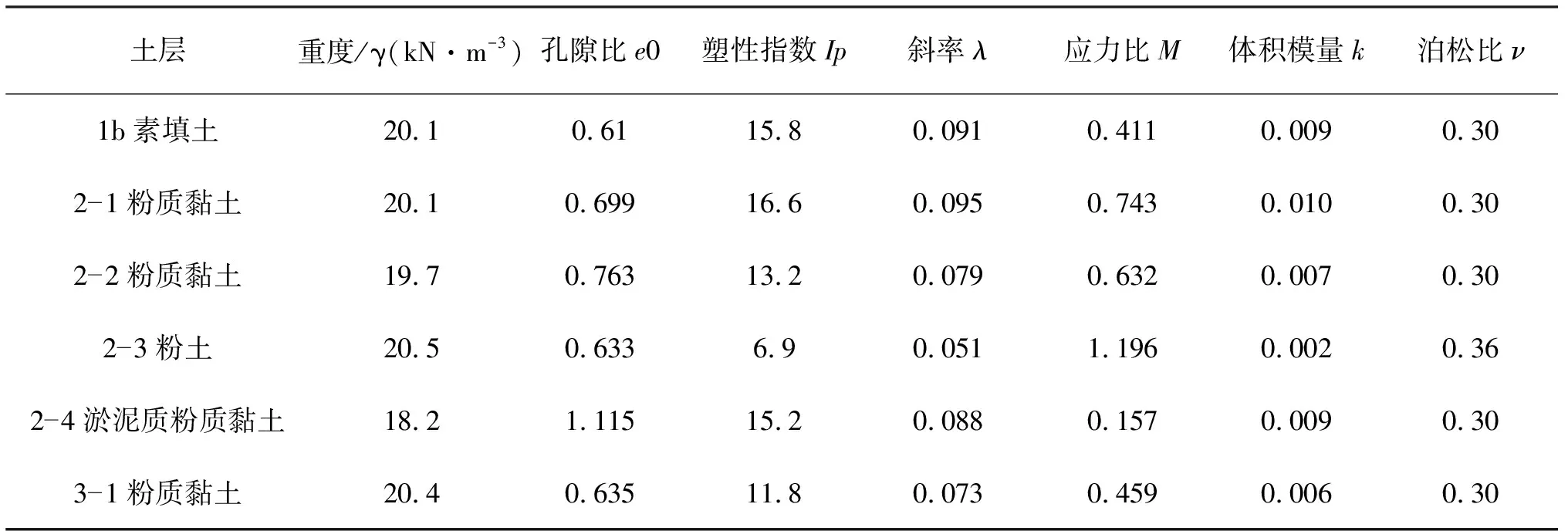
表1 各土层计算模型材料参数
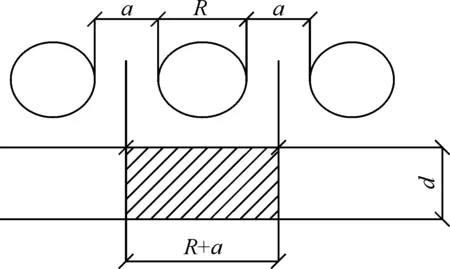
图2 排桩墙与连续板桩墙等刚度换算示意图
3.2 施工工序模拟
根据工程的实际施工工序,本次施工过程共分2层开挖、2层回填。通过单元的“生死功能”来实现土体的开挖、回填及支护结构和隧道结构的施加[8]。施工过程的具体分析步骤如下:
步骤1:初始地应力的平衡。建立整个场地土体支护结构(支护结构、撑梁)及隧道结构的有限元模型,“杀死”除原始土体之外的所有单元,并施加重力,以平衡土体的初始地应力场;
步骤2:“杀死”第一层土体,以模拟大堤土体开挖;
步骤3:挖除支护内土体,并“激活”撑梁和支护单元,以模拟支护施加;
步骤4:“激活”隧道结构单元,以模拟隧道结构施工;
步骤5:“激活”隧道上部土体单元,以模拟隧道上部土体回填。
4 基坑开挖及堤防恢复变形性状分析
4.1 开挖面土体隆起
图3~5分别为太湖大堤堤身开挖后竖向位移分布图、隧道基坑开挖支护后竖向位移分布图及隧道工程完工后竖向位移分布图。由图可知:(1)堤身开挖后基底最大隆起位于基坑中心位置,为9 cm。基底平均隆起高度为8.3 cm;(2)隧道基坑开挖支护后,基底最大隆起位于基坑中心位置,为18.6 cm。基底平均隆起高度为16.6 cm;(3)隧道工程完工后,基底最大隆起位于基坑中心位置,为2.8 cm。基底平均隆起高度为1.4 cm;(4)基坑开挖面隆起高度随着开挖深度的增加不断增大,最大回填达到18.6 cm。且在隧道完工后,由于受到荷载作用,基底隆起高度相应减小。

图3 堤防开挖竖向位移云图
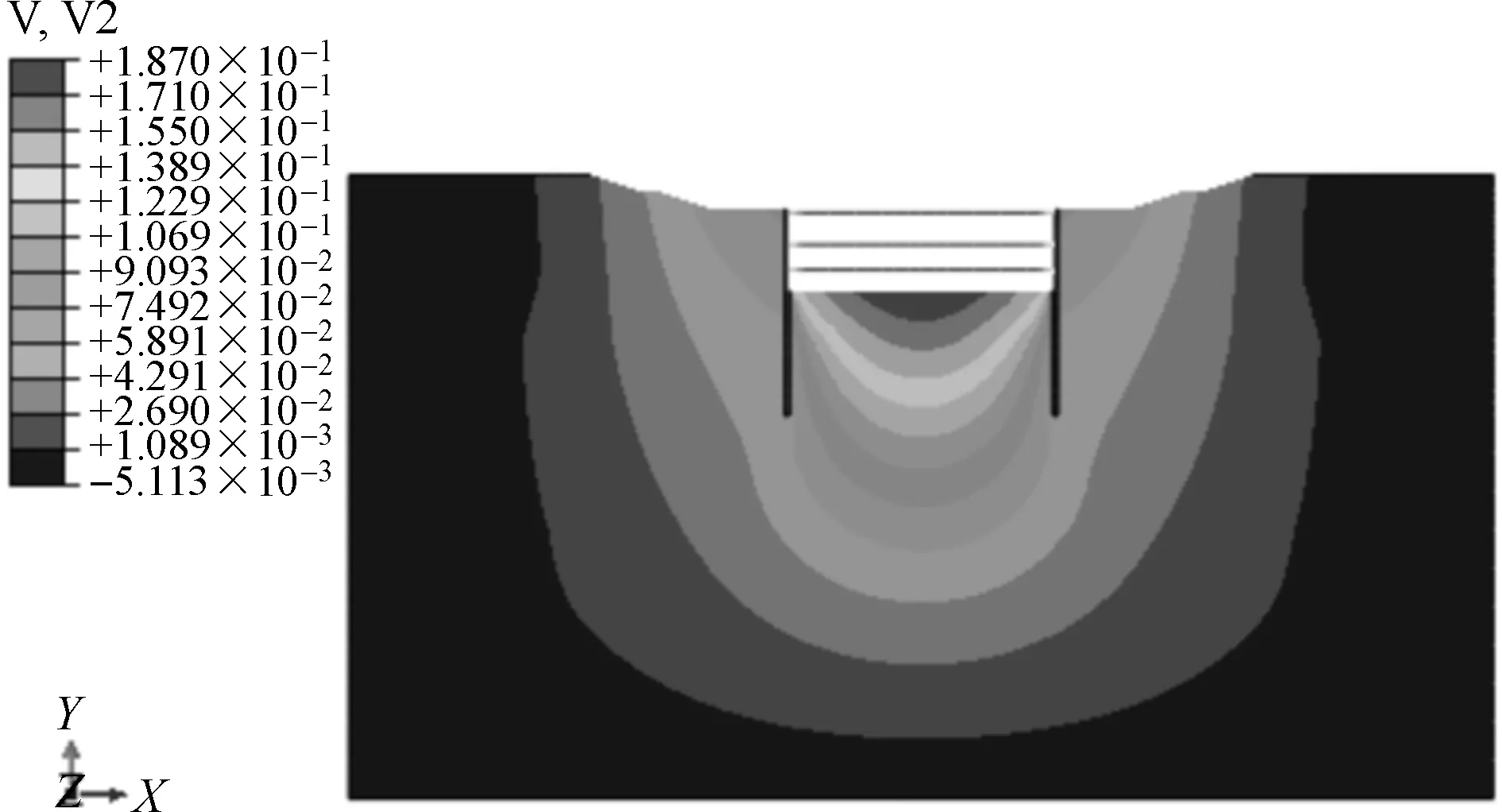
图4 基坑开挖竖向位移云图
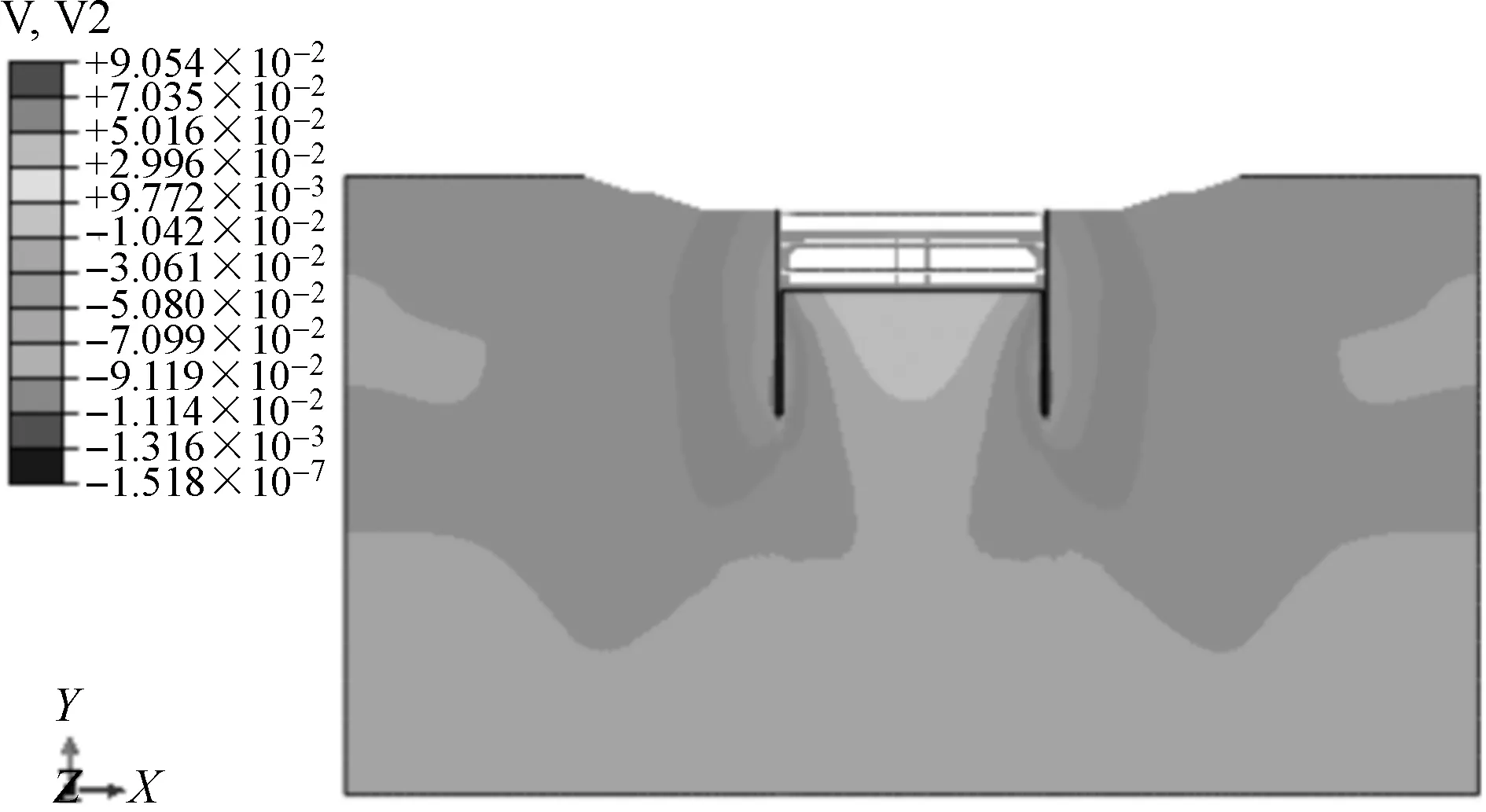
图5 隧道完工后竖向位移云图
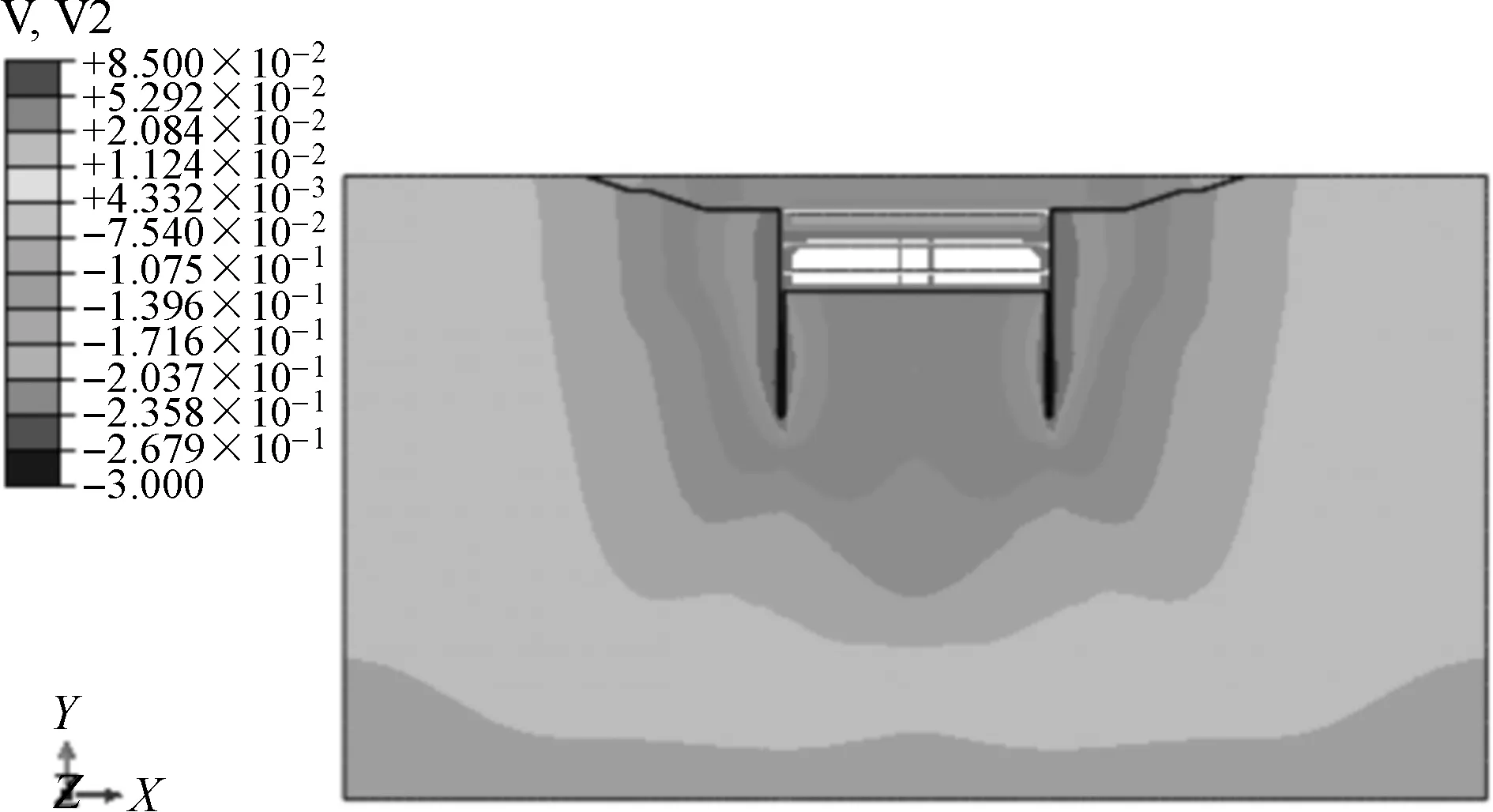
图6 堤防恢复竖向位移云图
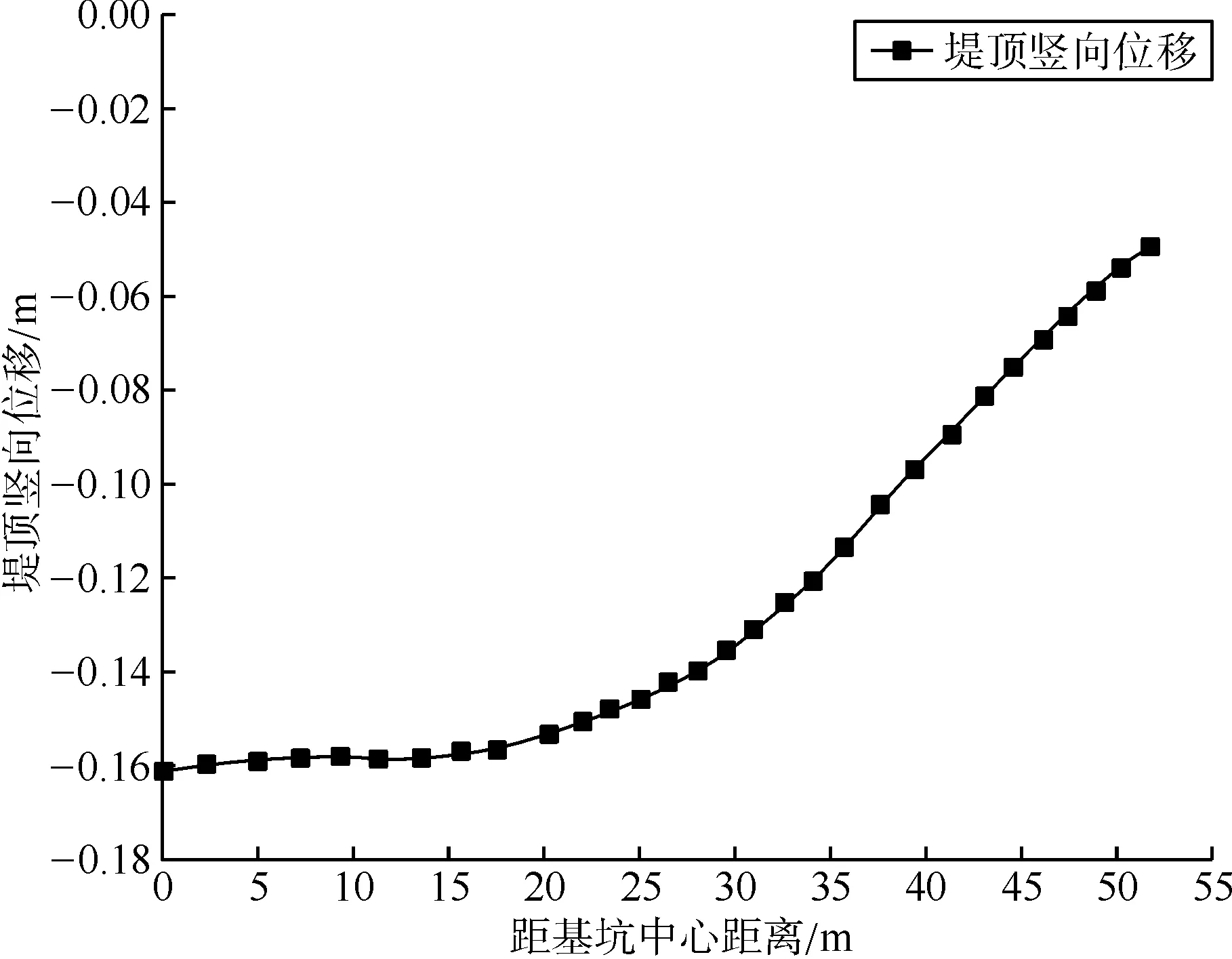
图7 恢复段堤顶竖向位移曲线
4.2 恢复段堤防沉降变形
图6为堤防恢复后竖向位移分布图,图7为恢复段堤顶竖向位移曲线图。由图7可以看到堤防恢复后,堤顶最大沉降位于恢复段堤防中心位置,为15.8 cm。恢复段堤顶平均沉降为12.1 cm,小于堤身高度的3%。
4.3 有限元分析与规范计算堤防变形对比
根据GB50286—2013,堤防沉降计算采用分层总合法[9],计算公式如下:
(2)
式中:S为最终沉降量;n为压缩层范围的土层数;e1i为第i土层在平均自重应力作用下的孔隙比;e2i为第i土层在平均自重应力和平均附加应力共同作用下的孔隙比作用下的孔隙比;hi为第i土层的厚度;m为修正系数,可取1.0,软土地基可采用1.3~1.6。
经计算,恢复段堤防沉降量为15.2 cm。本次堤防恢复后,恢复段堤顶共布置了4处沉降位移观测点,累计沉降量分别为7.9 cm、5.4 cm、8.2 cm及5.8 cm,恢复段堤防累计沉降平均值为6.83 cm。见表2。

表2 恢复段堤防沉降值对比
通过对比可以看出,考虑应力路径的有限元分析计算的沉降值较规范采用的分层总合法计算的沉降值,与实际沉降值更接近、更符合实际情况。
5 结 语
本文基于恢复段堤防施工工序,采用修正剑桥模型(MCC)对工程建立了有限元计算模型。通过模拟计算,得到基坑开挖面及恢复堤防土体变形形态,变形结果基本符合施工变形规律。重点对比了有限元法数值模拟与分层总合法计算成果,考虑施工过程的有限元法计算值与实测值较为接近。对于施工过程较为复杂的重要基坑,建议采用有限元数值模拟法计算更为准确。

