基于声固耦合理论对捕捞航行器的湿模态分析

刘义翔, 刘凌霄, 田 野, 关祥毅, 冯砚博

(1.哈尔滨商业大学 轻工学院 ，哈尔滨150028；2.中建三局集团有限公司，武汉430074)

目前对捕捞作业水下航行器的研究亟待深入，然而民用水下航行器发展受传统设计的制约.民用水下航行器的研制始于20世纪80年代初，其主要用于的海洋资源勘测、海上石油天然气的开发、海洋水产品养殖等.

近年来，水下航行器得到了迅速发展，在海洋养殖捕捞器、科研探测等领域应用较广泛，但由于其特殊的工况，不易于进行试验，因此利用ANSYS软件进行相关数据的分析很有必要[1-2].水下航行器在工作时，会受到周围水介质的作用，产生流固耦合效应[3].因此对其湿模态进行分析，取前十阶模态，分析水下环境对于航行器的振动特性的影响.

本文的水下航行器是一个典型框架型机器.机器本体结构由主体框架和内部控制设备组成，其外部框架作支撑整体机器的运行，如若碰到礁石或其他障碍物，未能及时躲避的话，它可保护机器的内部结构不被损坏.机器本体的前端装有图像采集装置，以保证机器能将航行时的水底工况与周围环境及时向控制器反馈.机器本体结构的两侧浮力装置能完成机器的下潜或者上浮[4]，中间段装有控制器，推进器结构安装在机器本体末端或中段，它是机器的动力来源[5].

作为典型的水下航行器设计分为框架型与流线型设计，综合考虑水下的实际工况，它们都具有其局限性.考虑到工作目标是进行拾取海底养殖的海产品收集，流线型航行器在自身负载方面优于框架型航行，故此决定采用流线型水下航行器进行总体设计，使其能够完成养殖海产品捕捞的工作要求，该航行器本体的结构如图1所示.也称水下航行器.

该捕捞作业水下航行器结构上背负两个收集舱，对称放置，保持其在水下浮力作用下的稳定性，同时左右还各有两个活动捕捞装置，其活动空间较大，可灵活地拾取采集目标养殖海产品.收集舱外形以原流线型水下航行器的弧度设计，为了降低水的阻力采取半圆弧式的结构.除此还在航行器底部配有两个防撞轮，以保证机器在遇到海底礁石等不利环境时不被损坏.

捕捞作业水下航行器的关键技术在于，如何应对水下的复杂工况中，将机械设计、智能图像识别控制系统以及算法等多种技术进行融合应用[6].

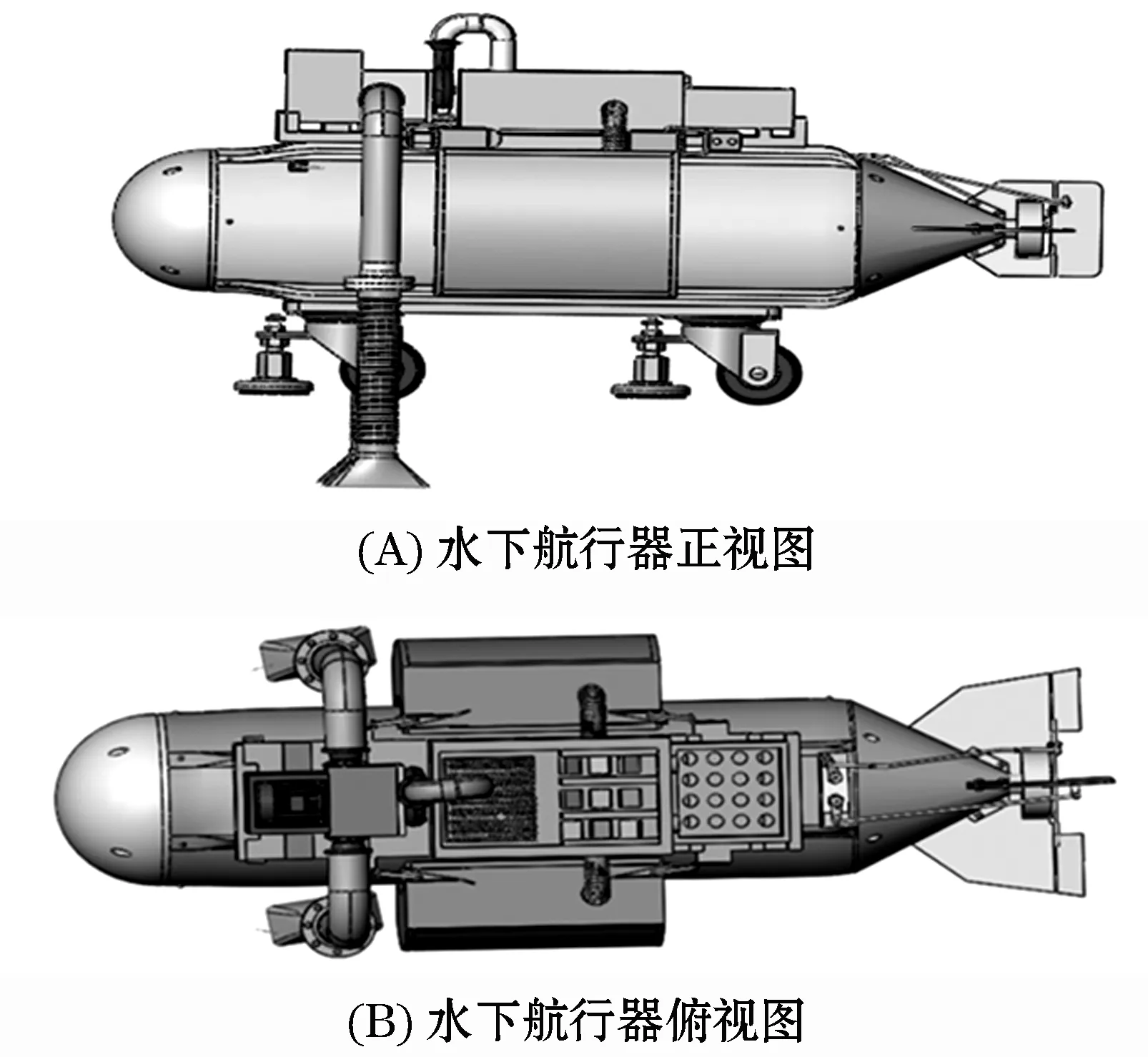
图1 水下航行器总体设计图Figure 1 Overall design drawing of underwater vehicle

机械系统设计的水下航行器是载体.机器本体外形主要是流线型框架式，其耐压壳体设计时，首先要满足深水载荷作用下的结构与强度要求；另外，必须采用密封结构以保护内部结构与电器元件，从而保证捕捞作业水下航行器的正常航行.该捕捞作业水下机器人的参数如表 1所示.

表1 捕捞作业水下航行器参数

用CFD仿真模拟捕捞作业水下航行器在流体中运动的情况，得到其在不同运动速度下的阻力系数和相应其他参数，以及各速度分布情况与压力云图等.因水下航行器在其最初设计时，可能达不到最优的性能，仿真可利于对优化设计进行指导作用.

1 理论基础

应用声固耦合基础对水下航行器的湿模态进行分析，将流体视为可压缩的声学介质[7-8]，流体对水下航行器的影响表现为作用在结构壁面的声压动载荷.

在进行耦合分析时，需要对流体及声固耦合水下航行器的模型做出如下基本假设：

1)流体是无黏和可压缩的；

2)声波振幅相对较窄，这样流体密度变化较小；

3)波传播与热力学过程是绝热的.

可压缩流体的Helhmoltz声学波动方程为[9]：

(1)

离散化后的流体波动方程用矩阵形式表示为[10]：

(2)

航行的水下航行器结构力学方程为[8]：

[KS]{U}-[R]{P}=[FS]

(3)

将方程(2)与(3)合并，得声固耦合方程：

(4)

其中：[Mfs]=ρ0[R]T,[Kfs]=-[R],[M]为质量矩阵，[C]为阻尼矩阵，[K]为刚度矩阵，{P}为流体声学载荷矩阵，[Mfs]为质量耦合矩阵，下标S为水下机器人结构，f为流体.

2 水下航行器模态分析

本文选取了典型的海洋捕捞水下航行器，并对其结构进行了简化以便于分析，在声固耦合方程的理论基础上，求得了航行器在水下悬浮状态的前10阶模态.

2.1 模态分析前处理

该水下航行器模型长1.065 m，半径0.075 m，壁厚0.1 m，采用合金钢材料，密度7 800 kg/m3,弹性模量2e+11Pa，泊松比0.3，材料为各向同性[11-12].

应用ANSYS Workbench软件，对该航行器设置流体包围域并划分网格，如图1所示，由于分析航行器在水下漂浮状态时的模态，所以不对其施加载荷及约束，基于公式( 4 )给出的声固耦合方程，求解出航行器在水下受流固耦合效应的前10阶模态.

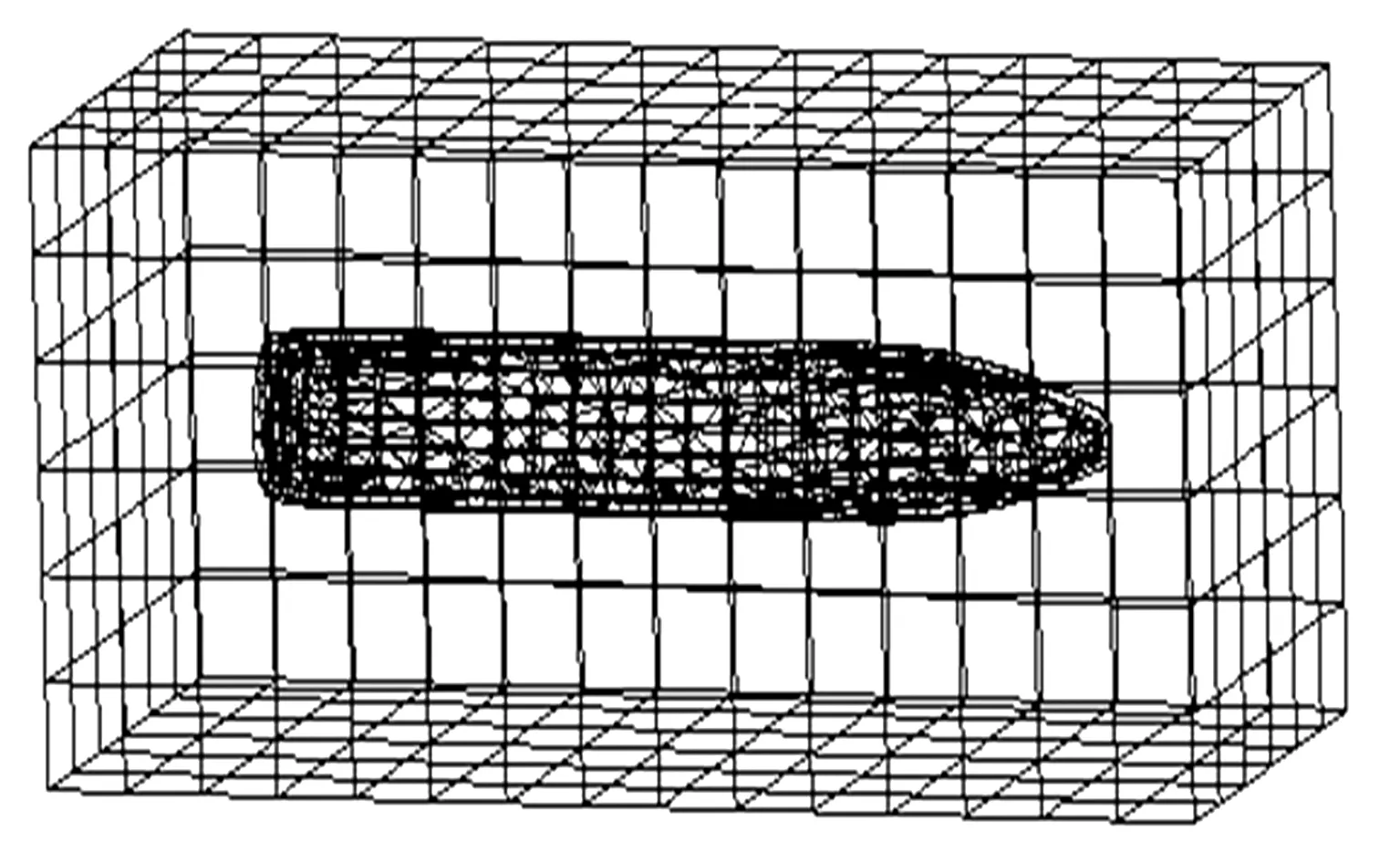
图2 水下航行器网格化分结果Figure 2 Meshing results of underwater vehicle

2.2 模态分析

由于未施加位移约束，故此计算的前6阶模态均为水下机器人的刚体模态，其值近似为0[13]，水下机器人第7阶至第10阶的频率如表2所示.第7阶至第10阶振型如图3～6所示.

表2 水下航行器第7～10阶频率

图3 第7阶振型Figure 3 7th Modal Shape Figure

图4 第8阶振型Figure 4 8th Modal Shape Figure

图5 第9阶振型Figure 5 9th Modal Shape Figure

图6 第10阶振型Figure 6 10th Modal Shape Figure

由表1可看出，该水下航行器在第9阶时频率发生变化较大，且频率较高，发生高频共振的可能性大[14]，结合各阶振型图可以看出，第7阶、第8阶的振型为弯曲振型，而第9阶、第10阶为扭转振型.同时水下航行器的位移在各阶模态下产生微小变动，对水下航行器工作状态影响有限，说明结构基本满足设计要求；但刚度不够，需要进一步优化.由于模型是对水下航行器进行了简化，只保留了壳体，因此在后续的设计中，需要对内部构件的设计进行合理安排，以尽量提高整体刚度，保持在水下工作时的稳定性[15].

3 结 语

基于声固耦合理论对捕捞作业水下航行器的湿模态分析，具有较大的实际工程意义，通过对其模态的分析，可检验结构能否满足要求，并进行优化设计.该捕捞作业水下航行器经过湿模态分析，根据其位移量大小与振型图，其外形结构基本满足设计及工作要求，但仍需要进一步优化，以更好地提高工作性能；同时根据提取的前10阶频率，还需要防范捕捞作业水下航行器发生高频共振现象.