基于Matlab的内孔定位机构的优化设计

晏祖根，宋晶宇，鲁 俊，陈 召，朱健瑜

(哈尔滨商业大学 轻工学院, 哈尔滨 150028)

对于产品运输，包装技术主要有传统的纸板箱式包装、缠绕膜包装、热收缩膜包装及冷拉伸套管包装.产品在运输过程中的完好性是降低企业成本的重要途经，通过采用先进的包装技术，保证产品质量，提高包装效率，给企业带来经济效益.拉伸膜有高透明度、低挤压力、高强度、较好的抗撕裂性能.冷拉伸套管膜包装具有工作效率高、保证货物安全可靠、视觉效果好等优势.此外，该套膜包装技术具有防水、防尘的包装效果，特别适用于电缆、塑料薄膜的包装，广泛应用于建筑、化工、食品等行业[1-7].

对于冷拉伸套膜包装的工艺，主要流程有托盘上料、放膜、拉膜、套膜、下料.在上料过程中，为保证包装膜的完整性及良好的物理保护性能，需要对托盘装载的货物准确定位.对于垂直放置的筒状物料，其外表面与拉伸膜直接接触，内表面用于定心.目前，中小尺寸筒状物料主要采用缠绕膜工艺，对垂直放置较大尺寸的筒状物料套膜以及垂直方向定心的研究还很少.

1 立桶冷拉伸套膜系统组成原理

1.1 铜导体立桶冷拉伸套膜需求分析

电线电缆产品因其自身的属性、销售需求和流通需求，需要满足较为严格的包装需求.电缆作为一种易氧化的金属制产品，同时也会受到光照及湿气的影响，导致材料变质或损伤，材料的包装与产品质量有直接联系.同时，当今消费市场处于饱和状态，消费者选用产品时也会考虑产品包装的美观、环保等，产品包装的好与坏直接影响产品的销售量.另外，产品从出厂到用户手中要经历多次的运输、搬运、仓储等环节，这要求包装方式应满足方便搬运、运输等.以上需求充分验证了包装的必要性[8-9].传统的电线电缆的产品包装以木材为主，因为木材加工方便，成本低廉.随着人类环保意识及新产品包装要求的提高，包装形式发生了变化.拉伸套膜作为一种新型包装材料，因其良好的保护性能、优越的成本和效率、优越的外观透明性以及在重量、环保的突出优势，在包装领域的份额不断增大.在电缆产业中，为保证产品在运输过程中的完整性，对桶状物料的包装提出了较高的要求.

如图1所示，铜导体立桶是由运输工艺横梁、托盘、铜导体、约束内圈和约束外圈组成.运输工艺横梁可供AGV叉车叉起或放下立桶，实现不同工位间的运输.托盘、约束外圈及约束内圈可限制铜导体径向及轴向窜动，同时也保护铜导体不会因外力而变形.考虑到铜导体产品的自身属性，销售及流通需求，现采用拉伸膜包装铜导体立桶，即拉伸膜包裹于约束外圈的外侧，完成包装.目前，该立桶套袋方式采用人工套袋，因铜导体立桶的径向尺寸为1 070 mm，轴向尺寸为1 980 mm，人工套袋的成本较高，包装质量差，不美观且套袋易脱落.现使用套膜机构对铜导体立桶进行套膜，可实现快速、高效、高质量的包装.

1.2 铜导体立桶冷拉伸套膜系统工作原理

铜导体立桶冷拉伸套膜系统是由多个机构组成.如图2所示，该系统由套膜机构、立桶定位机构、撑膜机构、导膜机构、薄膜封切机构等组成.成品膜卷由拉膜机构拉出薄膜，经导膜机构运行到系统上端，供膜机构停止工作，贴标机构将相关的产品信息打印并贴上绷直的薄膜表面.供膜系统继续工作，撑膜机构中的真空吸盘将薄膜吸附，机构杆组动作将薄膜由“一”字型转化为"口"字型，套膜机构中的平面机器人将已成型的“口”字型薄膜转化为“O”.供膜机构继续工作，当膜长度到达指定长度时，供膜机构停止工作，封切机构将薄膜通过加热将薄膜封口，并切断薄膜.套膜平台向下运动，将成型的膜向下包裹立桶，套膜机构脱离薄膜，薄膜在自身收缩作用下紧紧附在立桶外侧，完成套膜过程.

2 立桶定位部件总体设计

2.1 铜导体立桶定位要求分析

在立桶套袋过程中，受拉伸膜的开裂伸长率、伸长比及张力比等性能参数的约束，以及输送过程中的误差，为保证良好的包装效果，套袋工位立桶的许用位置误差仅为±10 mm，因此有必要对立桶进行轴向定位，以满足包装要求.如图3所示，铜导体立桶的外侧尺寸为1 070 mm，高度为1 980 mm，托盘内孔尺寸为450 mm，其托盘底部的方钢用来支撑立桶，同时提供AGV叉车工作的必要空间.立桶在满桶时的质量为2.0 t，定位过程中通过克服方钢与套袋工位的摩擦力来实现径向定位.

考虑到上料，托、放物料出现的误差及套袋工位对铜导体立桶定位的高要求，在套袋工位设置有定心机构.在套膜过程中，整个物料筒外侧需覆盖薄膜.若使用外圆定位，不利于套膜甚至可能会破坏薄膜.若采用内孔定位，不会干扰套膜过程，且内圆不易受到外界载荷而变形，定位精度较高.故采用内孔定位方式完成定心.

2.2 铜导体立桶定位机构方案

由于铜导体立桶底部设置有通过圆孔轴线的横梁，且立桶质量较大，采用三组杆件机构共同作用来实现定心动作时，对动力源及杆件的要求较高且定心精度低和稳定性较差，为提高定心过程中的稳定性及定位精度，采用四组杆件共同作用实现定心动作.

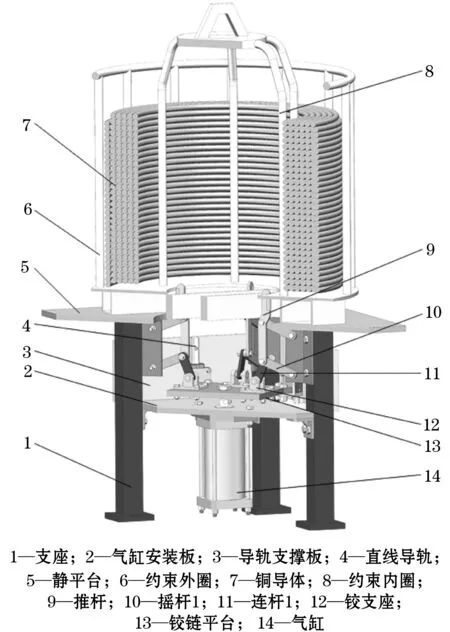
图4 内孔定心机构示意图Figure 4 Schematic diagram of inner hole centering mechanism

如图4所示，机构的内孔定心机构由气缸、静平台、铰链平台、铰支座及杆组等组成.气缸固定在气缸安装板上，活塞与铰链平台通过螺栓连接，提供给铰链平台升降运动.气缸安装板与支座通过螺栓连接固定在机架上.铰支座与杆组连接，通过铰链平台的升降驱使杆组中的推杆9“收缩”或“扩张”，其“扩张”过程即为定位铜导体立桶的过程.在初始状态，气缸活塞未伸出，推杆9为“收缩”状态，即4组杆组中推杆形成的圆直径最小，方便立桶进入该工位.当铜导体立桶进入该工位后，气缸驱动铰链平台向上运动，杆组在气缸的作用下运动.在该过程中，4组推杆所形成的圆的直径逐渐变大，推杆与内孔接触并施加载荷，立桶在外部载荷作用下稳定移动.当活塞达到最大行程时，4组推杆所形成的圆的直径为最大值，此时，4组杆组与内孔全部接触，即内孔与杆组中心同轴，完成定位.

3 立桶定位部件的机构分析

3.1 立桶定位机构总体模型

如图5所示，立桶定位机构由原动件、传动部分和执行部分组成.原动件为气缸，气缸固定在机架上，其活塞与铰链平台锁定连接，即气缸可直接控制铰链平台的升降.传动部分为4组均布杆组.其中，铰链平台上的铰支座与杆组连接，通过平台的升降运动驱动杆组运动.执行部分为平行四边形的连杆部分，通过连接固定铰链点杆件的摆动实现连杆的保持竖直的平动，从而完成定心过程.

图5 内孔定位机构结构简图Figure 5 Instruction diagram of inner hole centering mechanism

3.2 立桶定位机构的受力分析

如图6所示，铜导体立桶在定位过程中，四组均布的推杆在气缸的驱动下向外“扩张”，完成定心.由于AGV叉车上料位置及取料位置的差异，立桶会在一定范围内随机放置.对于不同的立桶位置，各推杆施加给立桶的力是不同的.

现按照极限位置及推杆最大受力计算，即立桶位于极限位置，且定心过程仅有一组推杆来完成.铜导体立桶的满桶质量为2.0 t，钢与钢间的摩擦系数取0.15，则定心过程中，立桶的摩擦力f为

f=μmg=3 000 N

即推杆输出力的最小值为3 000 N.

4 单支链定位机构建模

内孔定心机构的总体机构如图5所示，对于四组周向均布的杆组，其运动特性相同.现单独研究一组杆件运动，单独一组杆件的运动简图如7所示，该机构是由机架、原动件和基本杆组三部分组成.当给定原动件滑块特定的运动参数，基本杆组有确定的运动.

图7 单组杆件运动简图Figure 7 Instruction diagram of single group linkage

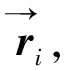
滑块-摇杆机构的运动简图如8所示，该机构是由滑块1、连杆2和摇杆3组成.滑块1为主动件，摇杆3为从动构件，滑块1的上下移动转化为摇杆3的往复摆动.由上一节可知滑块、杆件i的定义内容，现可建立机构的矢量方程.

图8 滑块-摇杆机构运动简图Figure 8 Instruction diagram of slider-rocker mechanism

根据8及封闭矢量多边形方程，机构的角位移矩阵分量形式为：

(1)

将式(1)对时间t求导，机构的角速度方程分量形式为：

(2)

将式(2)对时间t求导，机构的角加速度方程分量形式为：

(3)

根据图3的几何关系及余弦定理有：

(4)

(5)

根据实际空间布置，现初定杆件尺寸：l2=80 mm，l3=120 mm，e=145 mm.通过Matlab编程可求解出满足推理条件的原动件的驱动力Fq大小.此时θ2=-48.068 3°，θ3=40.285 0°,Fq=6 239.25 N.当气源压强P为0.6 MPa时，可求解出原动件气缸的缸径d，从而对原动件进行选型.

故气缸活塞实际直径D应满足D≥d，取直径为125 mm的气缸作为驱动气缸可满足条件.

5 单支链定位机构优化设计

为进一步研究机构运动性能与动力性能，须确定各构件的尺寸和位置参数，可采用Matlab优化工具箱函数处理该问题.在实际的优化设计过程中，主要有三个步骤：1)建立优化的数学模型，即确定设计变量、建立目标函数和确定约束条件；2)根据实际问题选择适当的优化函数；3)进行优化计算，确定出各构件的位置和尺寸参数[10].

5.1 确定设计变量

在设计过程中进行选择，且最终必须确定的相互独立的量称为设计变量.在该机构中，各杆件的长度l2,l3,l4,l5,l6及滑块的偏心距e为待定量.对于此机构，有l3=l5,l4=l6.因此，设计变量可表示为：

x=[x1x2x3x4x5]T=[l2l3eθ2θ3]T

该设计变量为5维设计变量，属于小型优化设计问题.

5.2 确定约束条件

在实际应用中，设计变量在取值时通常会受到多个条件的限制，满足所有约束条件的公共区域称为可行域，通过将可行域中的各个点的坐标代入目标函数，求解得到最符合目标函数的解，这就是设计变量的最优解.约束条件又可分为几何约束和性能约束.

在该机构中，滑块为主动件，摇杆为从动件.为避免机构出现“死点”，杆件OB不可做周转运动，即l3+e>l2.写成不等式约束条件为：

g1(x)=x1-x2-x3≤0

(6)

在连杆机构运动学的优化设计问题，为了获得最佳的传力性能，要求选择最佳的运动学参数，而优化设计往往根据机构运动学参数来建立目标函数.如图9所示，该机构由滑块-摇杆机构OAB与平面连杆机构OBCD串联而成.为使机构具有良好的运动特性，两个机构元素的传动角γ1,γ2大于等于许用传动角[γ].该机械结构传递的功率较大，故选择许用传动角[γ]为 40°[11-12].γ1,γ2越大，机构的传力性能越好，对传动越有利.传动角γ1,γ2可作为性能约束条件.

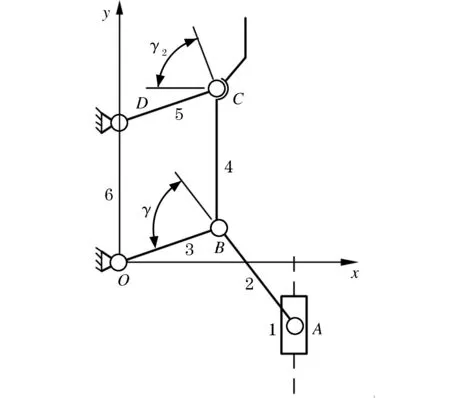
图9 机构的传动角Figure 9 Transmission angle of mechanism

其中：传动角γ1,γ2应满足γ1,γ2≥40°，经过整理，得到约束方程：

(7)

g3(x)=cos|x5|-cos40°≤0

(8)

在机构的实际工程应用中，各杆件的尺寸受到工作空间的限制.现对构件3的尺寸要求：10

经过整理，得到的约束方程为：

g4(x)=20-x2≤0

(9)

g5(x)=x2-250≤0

(10)

g6(x)=20-x3≤0

(11)

g7(x)=x3-150≤0

(12)

g8(x)=-90°-x4≤0

(13)

(14)

g10(x)=-x5≤0

(15)

g11(x)=x5-50°≤0

(16)

此外，在机构的整个运动过程中，不仅需要满足以上不等式条件约束，考虑到机构的杆长条件，整理得：

(17)

综上，式(6)～(17)构成杆件优化设计的约束函数，对设计变量的取值范围进行约束.

5.3 建立目标函数

在建立目标函数时，以原动件的最优选择为目标，即以最优的气缸缸体直径为目标.如图(9)所示，该机构是由滑块-摇杆机构OAB与平面连杆机构OBCD串联而成.选用原动件时，通过改变构件尺寸能使机构拥有良好的传力性能.考虑到机构的传动性能，在建立目标函数时，选择原动件驱动力的大小作为评判机构性能的重要指标.现采用fmincon函数对实际问题进行优化.

图10 机构力矢量图Figure 10 Mechanical force vector diagram

整个系统的力矢量图如图10所示，在计算滑块的驱动力FA时，通过各杆件的受力分析可知：

在使用优化函数时，目标函数需整理为最小值函数，代入设计变量得：

在机构传力过程中，摇杆滑块机构OAB的传动角γ也应尽可能大，可建立目标函数:

综上，目标函数方程为

5.4 Matlab优化工具箱优化求解

Matlab优化工具箱(Optimization Toolbox)包含一系列优化算法和模块，可以用于求解线性规划和二次规划、函数的最大和最小值、非线性规划、多目标优化、非线性最小二乘逼近和曲线拟合、非线性系统方程和复杂结构的大规模问题[13-15].根据上节描述，本例属于一般的约束非线性目标规划问题，其标准形式为：

其中：f(X)是目标函数.

调用Matlab优化工具箱中的非线性规划函数fmincon求解器进行求解.其使用形式为：

[x,fval, exitflag]=fmincon(@Objfun, x0,A,b,Aeq,Lb,Ub,@nonlcon)

其各个参数的含义如下：x为返回目标函数的最优解，fval为返回目标函数在最优解x点的函数值，exitflag为整数标识算法终止的原因，Objfun为调用多目标函数的函数文件名，x0为变量初始值，A、b为线性不等式约束条件的系数矩阵和常数向量，Aeq、beq为线性等式约束条件的系数矩阵和常数向量，Lb、Ub分别为设计变量x的下界向量和上界向量，nonlcon为定义非线性约束的函数名.

5.5 设计实例

对于该5维多目标优化问题，结合优化数学模型及优化函数，编制关于优化设计数学模型的目标函数文件、约束函数文件和主文件.

运行程序得：

x=[103.780 9;141.283 0;122.543 5;-1.0471;1.047 1]

fval=4 621.21;

经过迭代计算得到最优解：l2=103.780 9，l3=141.283 0，e=122.543 5，θ2=-1.047 1，θ3=1.047 1，再依据实际工况转化为凑整解.凑整解为：l2=105，l3=140，e=120，此时，θ2=-60.350 9°，θ3=60.913 6°,Fq=4 621.21 N.当气源压强P为0.6 MPa时，可求解出原动件气缸的缸径d：

标准气缸可选择缸径D为100 mm的气缸.凑整解可满足传动角要求，此时机构具有较好的传力特性，优化结果满足要求.

6 立桶定位机构建模

确定好各杆件尺寸后，根据凑整后的连杆尺寸建立三维模型，如图11所示.其中，l2=105，l3=140，e=120，气缸在0.6 MPa的气源供应下仅需要选用缸径为100 mm、行程为150 mm的气缸即可完成定心过程.定心机构所容许的误差为±50 mm，即铜导体立桶放置误差在目标位置轴心50 mm范围内可通过定心机构完成定心过程.为立桶套袋提供了条件.

图11 优化后的机构示意图Figure 11 Schematic diagram of optimized mechanism

7 结 语

本文研究了铜导体立桶的内孔定位机构，并结合实际问题对其杆件进行优化设计，对原动件的选型有指导作用.通过套膜系统机构分析、定位机构原理阐述、建立优化设计的数学模型、使用Matlab软件求解出机构的最优尺寸参数，选择出适当规格的气缸，且机构中杆件尺寸比值对实际工程实践有一定的指导意义，为串联杆件的优化设计及原动件选型提供了一种思路.