非马尔科夫环境中各向异性海森堡自旋链的几何量子失协
唐诗生, 李瑞鸣, 艾合买提·阿不力孜
(新疆师范大学 物理与电子工程学院物理系,乌鲁木齐 830054)
1 引 言
自然界中普遍存在着关联现象[1],量子关联中的量子纠缠是量子信息处理过程中的一种重要的资源[2],因此纠缠在量子计算和量子信息中起着至关重要的作用[3].在过去的几十年里研究者们对量子纠缠[4]的研究取得了很大的进展,并从实验和理论上发现量子关联不仅有量子纠缠还有量子失协、几何量子失协等.为了更清晰地描述量子关联,Ollivier和Zurek[5]引入了量子失协(QD).量子失协是一种非经典关联的信息论[6]度量方式.量子失协能够很好的度量两个子系统之间的关联.但它的评估过程非常困难,只有在某些特殊的情形下才能被评估,比如:贝尔对角态[7]、X型结构态[8].为了解决这一问题,Dakic等人[9]从测量距离也就是从几何角度引入希尔伯特-施密特(Hilbert-Schmidt)范数并提出了几何量子失协(GQD).几何量子失协是一种新的度量量子关联的方法并被广泛研究[10,11].
考虑到实际中的物理系统完全封闭是不可能存在的,系统不可避免地受到周围环境的影响从而导致量子态之间的关联特性被破坏.基于此原因,研究开放量子系统之间的GQD随时间的演化关系是很有意义的.按照外界环境对开放性量子系统的影响程度可划分为马尔科夫环境和非马尔科夫环境[12].其中马尔科夫环境没有环境记忆效应,即所研究的系统中的信息和能量只能从系统流到环境,而不能由环境反过来影响系统;非马尔科夫环境有环境记忆效应,也就是系统—环境之间有信息、能量[13]等的交换.在非马尔科夫环境下,系统现在的状态受系统历史状态影响.
1998年Diosi等人[14]系统的阐述了非马尔科夫量子态扩散方法(NMQSD),并采用真实的物理系统研究了量子关联在非马尔科夫环境下的演化性质;Laine等人[15]用纠缠的光子极化后产生的极化态实现了量子隐形传态;Jing等人[16]研究了在两种噪声情形下关于量子隐形传态的时间演化;Yu 等人研究了费米库,写出了系统在费米库中的NMQSD主方程[17,18];赵新宇等人[19,20]讨论了基于非马尔科夫费米库环境中双量子点模型的量子纠缠特性;Hu和Fan[21]研究了几何量子相关测度的演化方程;Hu等研究了多体的几何量子失协[22];Spehner定义了一种新的量子关联度量并测量了几何量子失协[23];Paula等通过考虑广义Schatten p范数重新讨论了几何量子失协[24];Lü等人研究了光子晶体腔阵列系统中的冻结高斯量子失协[25];Yang等人研究了光子晶体腔中分离的氮空位中心之间量子相关性的非马尔可夫动力学[26].但目前还没有研究在非马尔科夫环境中具有时变磁场和Dzyaloshinski—Moriya相互作用Dz下的两比特各向异性海森堡自旋链的几何量子失协.本文中,主要研究了非马尔可夫环境下海森堡XYZ模型中的几何量子失协并通过非马尔科夫量子态扩散方法进行了数值模拟.
2 几何量子失协的度量

(1)
其中xi=trρ(σi⊗I),yi=trρ(I⊗σi)为布洛赫矢量的分量,σi(i=1,2,3)是1925年泡利研究费米子时提出的泡利矩阵,Rij=Trρ(σi⊗σj)是关联张量的分量.对于二比特海森堡自旋链系统的量子态,量子零失协态的式子如下:
x=p1|ψ1〉〈ψ1|⊗ρ1+p2|ψ2〉〈ψ2|⊗ρ2
(2)
式中的{|ψ1〉,|ψ2〉}是正交规范基矢量.按照参考文献[28]能够知晓:在任意的二比特系统中几何量子失协的表达式能够重新表述为以下的等式:
(3)
式中列向量x=(x1,x2,x3)T,矩阵K=xxT+RRT的最大本征值定义为Kmax.实际上对于二比特系统的几何量子失协有一种简明扼要的计算方法可供选择,查阅参考文献[29]可得知,
(4)
其中λi是3×4阶矩阵R′=(x,R)的本征值.需要特别提醒的是:几何量子失协并不是归一化的,在二比特海森堡自旋链系统这种特殊的情形下,几何量子失协的最大值为0.5.
3 模型与方法
在实际中,由于固态量子系统具有优异的可操控和扩展的性能,因此通常首选固态量子系统作为量子信息的系统[30].其中Heisenberg自旋链模型是一个相对简单、有用的固态物理系统,因此在量子信息传输、量子计算方面得到了广泛的发展.本文选择了在非马尔科夫环境中具有时变磁场和Dzyaloshinski—Moriya相互作用中的自旋作用非常丰富的两比特海森堡XYZ模型作为研究的对象,此时系统的哈密顿量可以表述如下:
(5)
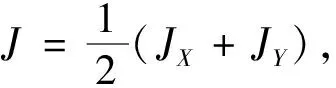
Htot=Hsys+Henv+Hint
(6)
其中,
(7),
(8),
(9).

(10).

在非马尔科夫环境下系统态演化的精确方程(方程(1))中可以明确地看见该方程内包含了一个时间非局域项,正是时间非局域部分的存在导致了方程的积分过程非常的困难甚至不可实现.因此在实际情形下就不得不运用一定的近似过程来处理方程(1).方程(1)中对时间有依赖的部分现在用操作符O(t,s,z*)来替代有下式,如下式所示:
(11)
通过一致性条件[35],
(12)
从一致性条件中就能够得到算子O(t,s,z*)的时间演化方程:
(13)
O(t,s,z*)=f1(t,s)O1+f2(t,s)O2+
f3(t,s)O3+f4(t,s)O4+f5(t,s)O5+
f6(t,s)O6+f7(t,s)O7+f8(t,s)O8
(14)
F1f1+F4f4-F1f3+F3f1+F3f4+F4f3-2iDzf3,
F2f4+F3f4+F4f3+F4f2+F2f2+F3f3+2iDzf4,
F2f1+F3f1+F4f2+F4f3+F2f3+F3f2+2iDzf1,
F1f4+F4f1-F1f2+F3f4+F3f1+F4f2-2iDzf2,
F4f8-F4f5+F5f1-F8f1+F1f7-
F2f5-F3f8-F4f7+F6f1-F7f1+2iDzf7,
F1f6+F2f8-F3f8-F4f7+F5f2-F8f2-F3f6-
F3f7+F6f2-F7f2-2iDzf8,
F1f7+F2f5-F3f5+F4f6-F5f3+F8f3-
F3f7+F3f6-F6f3+F7f3-2iDzf5
F4f5-F4f8-F5f4+F8f4+F1f6-F2f8-
F3f5-F4f6-F6f4+F7f4+2iDzf6
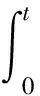
f1(t,t=s)=1,f5(t,t=s)=0,
f2(t,t=s)=1,f6(t,t=s)=0,
f3(t,t=s)=0,f7(t,t=s)=0,
f4(t,t=s)=0,f8(t,t=s)=0.
两比特海森堡XYZ系统中的量子态随时间演化的过程能够通过上述方程进行精确的数值模拟,量子态扩散方程能够简明紧凑地写为时间的局域方程,如下式所示:
(15)
4 数值模拟结果
利用量子态扩散方法得到了密度矩阵的时间演化过程,把随时间演化的密度矩阵代入系统的几何量子失协方程里,在非马尔科夫环境下通过数值模拟、计算、分析系统的几何量子失协随时间演化的过程.具体讨论了环境关联参数、海森堡自旋系统中两比特间的自旋耦合系数、时变磁场、Dzyaloshinski—Moriya相互作用Dz等参数在几何量子失协中的影响.下面分析各个参数对系统几何量子失协的影响.
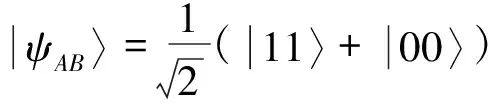





5 结 论
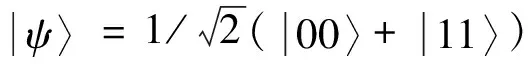
研究结果表明:在本系统中不同类型的参数对系统几何量子失协的影响不同.
(1)当环境关联系数取值越小也就是非马尔科夫性越强时,能够非常显著地提高系统的几何量子失协,因此非马尔科夫环境相比马尔可夫环境的优越性被体现.
(2)当自旋耦合系数J越大时能够非常显著地提高系统的几何量子失协.
(3)当时变磁场强度B越大时也能够非常显著地提高几何量子失协.此外,其它参数的选取在一定程度上对几何量子失协也有影响.
综上所述,在非马尔科夫条件下的两比特海森堡XYZ系统中,可以通过合理的组合各种参数实现较大的几何量子失协.

