基于主成分分析的供货商选择研究

摘 要：本文针对402家供应商进行量化分析排名。首先，整体分析A、B、C的需求量，整体的供货量，误差在某范围内的订单数。然后，个体分析每家供应商，确定评价指标，用主成分分析法各供应商按供应的原材料对应，将这个结果作为第一个指标。最后，利用SPSS求解，给出最终的供应商排名。

关键词：量化分析;主成分分析;SPSS

一、研究背景

某生产企业所用原材料总体可分为A、B、C三种类型。企业每年按 48 周安排生产，需要提前制定 24 周的原材料订购和转运计划，企业需要根据产能要求确定需要的供应商和订货量，确定转运商，并让转运商将供应商每周的供货量转运到企业仓库。该企业每周的产能为2.82万立方米，每立方米产品需消耗的各类材料用量以及各类原料的采购单价和储存费用。本文建立数学模型对402家供应商的供货特征进行量化分析，确定50家最重要的供应商。

二、基于主成分分析的模型

1.模型的建立

（1） 利用主成分分析算法对商家数量进行数学降维

问题一要求对 402 家原材料供应商进行量化分析，建立反映保障企业生产重要性的数学模型，并从中选出 50 家最重要的供应商。即从多个存在一定相关性的变量之间，当变量的个数较多且变量之间存在复杂的关系时，增加了问题分析的难度。可以采用主成分分析算法来解决这个问题，主成分分析是一种数学降维的方法，该方法主要将原来众多具有一定相关性的变量，重新组合成为一种新的相互无关的综合变量。

（2） 主成分分析算法相关介绍

基本概念：主成分分析，英文简写 PCA（Principal Component Analysis），提取数据集的主要特征成分，忽略次要特征成分，达到降维目的。

（3） 主成分分析算法特点

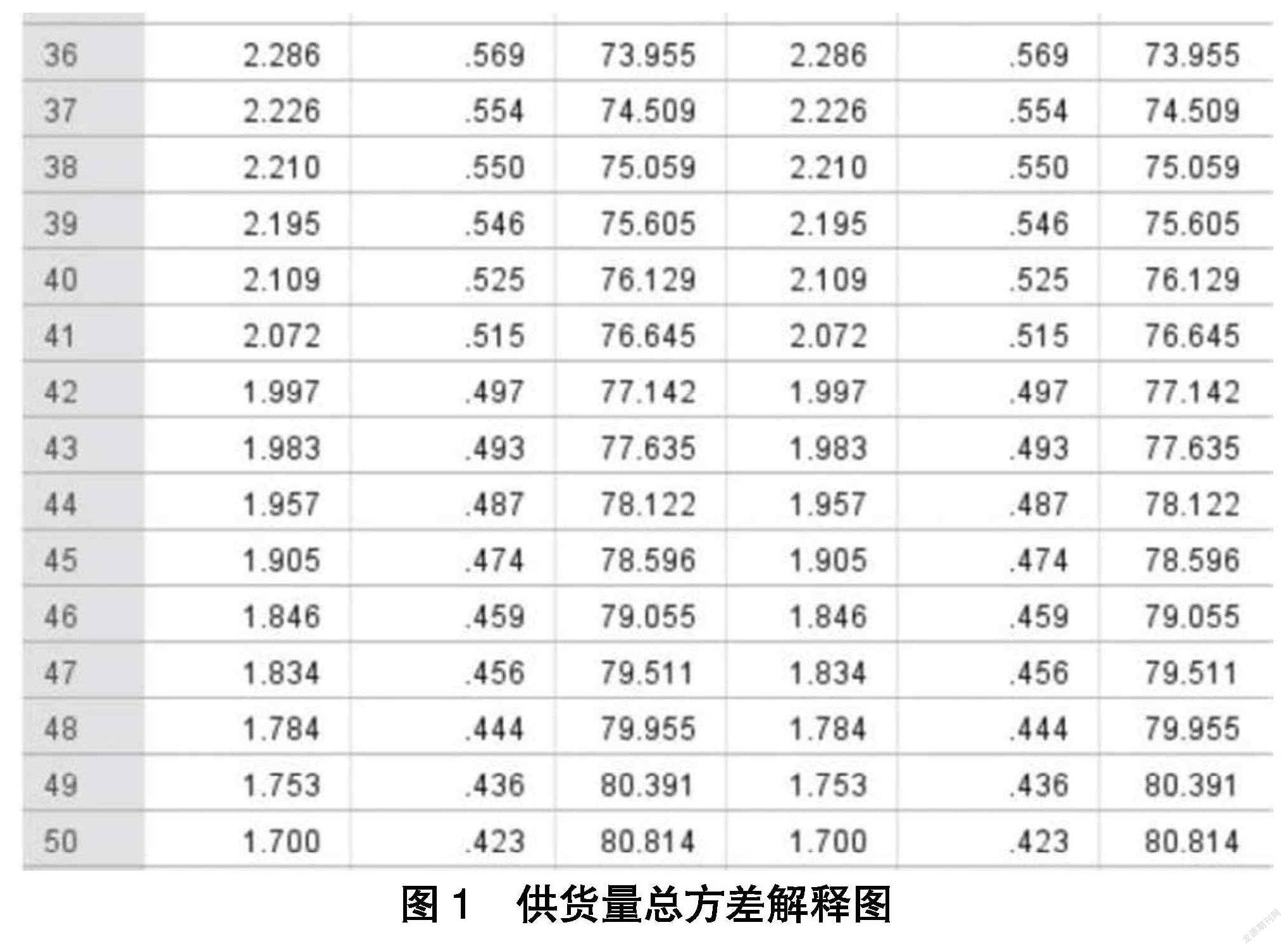
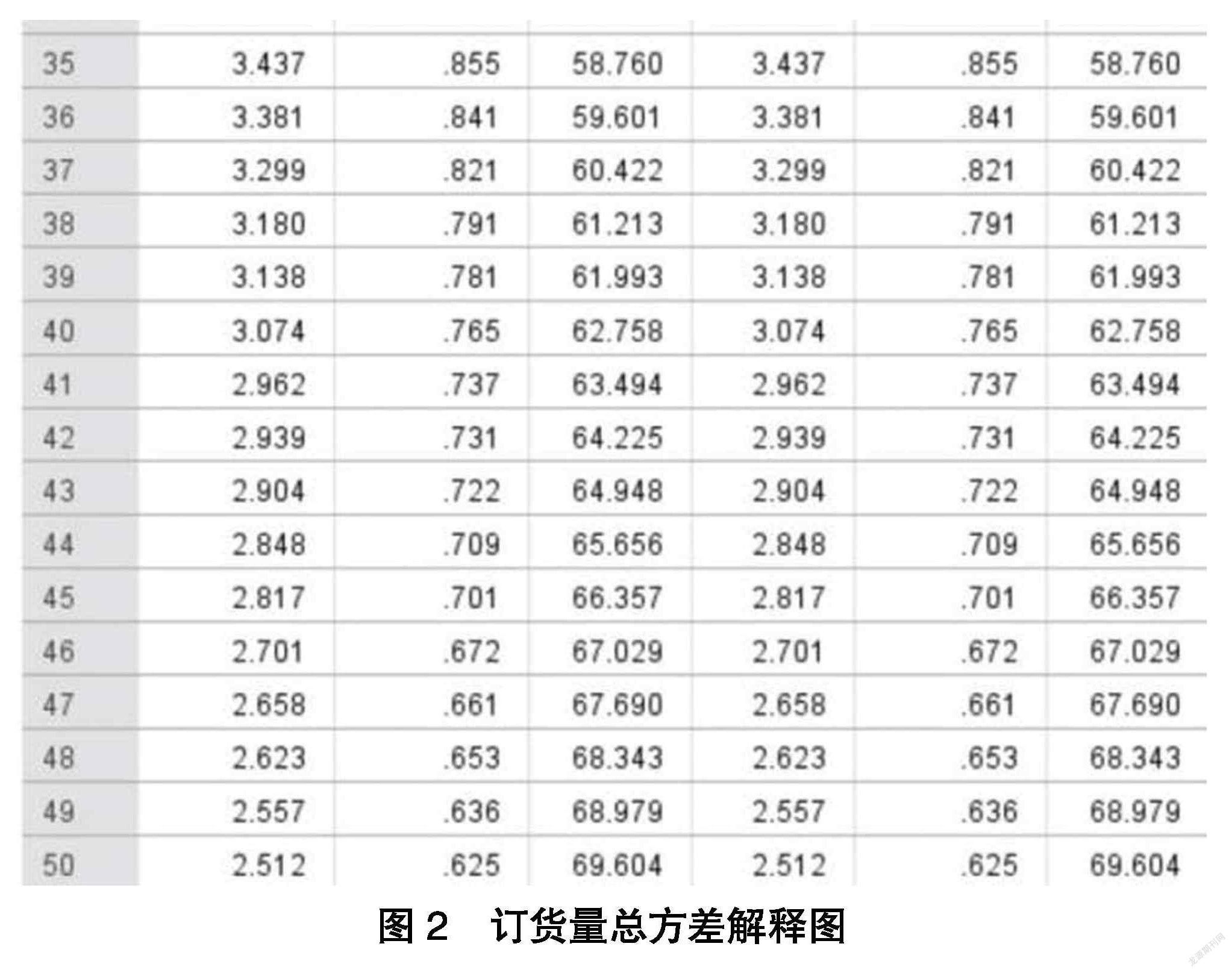
PCA 通过线性变换，将 N 维空间的原始数据变换到一个较低的 R 维空间（R

在降维过程中，不可避免地要造成信息损失。如原来在高维空间可分的点，在低维空间可能变成一个点，变得不可分。因此，要在降维过程中尽量减少这种损失。

特征之间的相关性越弱，则特征就越应该作为主要成分被保留。

反之，如果两个特征有较高的相关性，则只保留其中一个特征即可。为使样本投影到低维空间后尽可能分散，它们的方差要尽可能大。

（4） 主成分分析算法的基本思想

数据集 X 有 N 个特征，M 个样本。若将每个样本用列向量 xj（j=1，2，...，M）表示，则该数据集可以用下面的矩阵表示：

选择 N 个 R 维的正交基 pi（i=1，2，...，R）组成的矩阵：

所谓正交可以理解为两个向量 Pij（i≠j）相互垂直，即一个向量在另一个向量的投影为 0。

通过正交基将维数 N 降到 R 后，可能带来的一个问题是原本在 N 维空间可分的点，在 R 维空间变得不可分。

例如在三维空间上，位于垂直于某坐标平面的一条直线上的不同点，投影到该坐标平面上后成为一个点，从而使样本的可区分性丧失，造成信息丢失。

为了避免这类问题，降维的一个基本原则是，降维后的点（或投影后的值）在新的低维空间里尽可能的分散。

于是 PCA 问题就变成一个正交基的优化问题，即寻找一组最优正交基，使得将 N 维数据集的样本点投影到 R 维空间后，新的样本点在 R 维空间尽可能的分散。

方差是刻画样本分散程度的统计量。对特征xj（j=1，2，…，M），其方差为：

为了简化计算，将 xj 平移μ个单位，则样本均值变换为 0。

用 a 表示变换过的 x，上式变换为：

方差值越大，则特征 aj（j=1，2，...，M）的各个分量越分散。另外，对多维特征空间，如果两个特征是线性相关的，则这两个特征是冗余的，只保留一个即可。因此，降维后的特征间应尽可能不相关。刻画特征相关关系的统计量是协方差。协方差表示了两个随机变量 X，Y 同向（或反向）变化的程度。其绝对值越大，则同向（反向）变化的程度越明显，说明两者相关性越强。其值越接近 0，说明两者同向（反向）变化的程度越不明显，说明两者的相关性越弱。

对降维问题来说，希望保留下来的特征两两间是不相关的。因此要使其协方差的绝对值尽量小。由于各个特征经过平移，均值已为 0，因此有式：

特征均值为 0 的情况下，两个特征的协方差简洁地表示为其内积除以元素数 M。

当协方差为 0 时，表示两个特征完全独立。

为了让协方差为 0，选择基的方向一定是正交的。

则降维问题的优化目标为：将一组 N 维向量降为 R 维（R 大于 0，小于 N），其目标是选择 R 个单位（模为 1）正交基，使得原始数据变换到这组基上后，各特征两两间协方差为 0，而特征的方差则尽可能大。

即在正交约束下，取最大的 R 个方差。

多个特征两两间的协方差可以通过协方差矩陣来表示。

将数据集 X 的特征进行 0 均值以后记为 A，即式：

N 维特征向量的协方差矩阵：

PCA 的优化目标是在新的低维空间，特征间的协方差为 0，特征维数为 R.则应该寻找一个能使上式变换为形如下式的 R 阶对角方阵：

且对角线元素应是前式中对角线上前 R 个最大的元素，以满足特征方差越大数据越分散的要求。

令 P 为 R×N 单位对角矩阵：

至此，使用 P 将特征 0 均值化的 N 维数据集，降维至 R 维。

实际应用时，还需要保证留下来的 R 维空间中的特征内积（方差）之和最大，以使样本尽可能分散。

因此，要调整 P 的行向量与式（6-17）中对角线上最大的前R 个值相适应，以保证选择的 R 维向量方差之和最大。

对 M 条 N 维特征数据，PCA 算法步骤可以描述如下：

（1） 将原始数据按列组成 N 行 M 列矩阵 X;

（2） 将 X 的每一行（代表一个特征）进行零均值化，即减去这一行的均值;

（3） 求出协方差矩阵 C=;

（4） 求出协方差矩阵的特征值及对应的特征向量;

（5） 将特征向量按对应特征值大小从上到下按行排列成矩阵，取前 R 行组成矩阵 P;

（6） Y=PX 即为降维到 R 维后的数据。

本题主要采用主成分分析算法来求解问题。

2.模型的分析

（1） 利用 SPSS 进行主成分分析求解

使用 SPSS 软件对本模型进行主成分分析，根据近五年某 402 家企业订货量和供应商供货量中的数据，对表格中的数据分别进行量化处理，并将因子分析-选项-系数显示方式选择“按大小排序”，得到关于订货量和供货量的成分分析图。其中二者总方差累计的数据分别为 89.636%（供货量总方差解释图）和 89.727%（订货量总方差解释图），相差并不大。但是比较二者的前 50 项主成分总方差分析图发现，前 50 项二者的总方差累计的数据分别为 80.814%（供货量总方差解释图）和 69.604%（订货量总方差解释图），因此在从 402 家供应商中选择主要的 50 家供应商时，由供货量进行主成分分析的结果时更准确。

（2） 从成分矩阵中选择前 50 项得出最重要的 50 家供应商将因子分析-选项-系数显示方式选择“按大小排序”，得到关于供货量的成分矩阵图。从中选择前 50 项，即可确定最重要的 50 家供应商。

故对 402 家供应商的供货特征进行量化分析，建立反映保障企业生产重要性的主成分分析模型，确定 50 家最重要的供应商为 S259、S032、S401、S145、S389、S097、S164、S187、S399、S220、S278、S079、S018、S053、S061、S370、S106、S311、S316、S243、S302、S020、S029、S198、S043、S391、S107、S118、S230、S087、S354、S309、S274、S325、S171、S101、S052、S050、S006、S377、S021、S047、S249、S091、S398、S109、S048、S179、S205、S192。

3.模型評价

（1） 模型的优点

主成分分析法的优点：第一，可消除评价指标之间的相关影响。第二，可减少指标选择的工作量。第三，当评级指标较多时还可以在保留绝大部分信息的情况下用少数综合指标代替原指标进行分析，主成分分析中各主成分是按方差大小依次排列顺序的，在分析问题时，可以舍弃一部分主成分，只取前后方差较大的几个主成分来代表原变量，从而减少了计算工作量。

（2） 模型的缺点

主成分分析法的缺点：主成分的解释其含义一般多少带有点模糊性，不像原始变量的含义那么清楚、确切。

参考文献：

[1]杨玲玲，马良，张慧珍.多目标0-1规划的混沌优化算法[J].计算机应用研究，2012，29（12）：4486-4488.

[2]马龙，卢才武，顾清华，陈晓妮.多目标0-1规划问题的元胞狼群优化算法研究[J].运筹与管理，2018，27（3）：18.

[3]孙明涛，曹庆奎.基于遗传算法的供应链企业订购方案优化模型[J].2004，21（2）：87.

[4]苏学能，刘天琪，曹鸿谦，焦慧明，于亚光，何川，沈骥.基于Hadoop架构的多重分布式BP神经网络的短期负荷预测方法[J].中国电机工程学报，2017，37（17）：4967.

[5]杨海民，潘志松，白玮.时间序列预测方法综述[J].计算机科学，2019，46（1）：22.

[6]韩晓龙，李上，杨全业.基于遗传算法的战略供应链集成研究[J].计算机工程与应用，2018，54（2）.

作者简介：侯星竹（2001.12- ），女，汉族，辽宁省铁岭市人，渤海大学数学科学学院，本科在读