全要素生产率指数：演变、比较及展望

程开明，李泗娥

（浙江工商大学 统计与数学学院，浙江 杭州 310018）

一、引言

经济增长的可持续性及增长质量是各国或地区普遍关注的问题，而衡量经济增长质量的一个重要标准是效率的不断提升。全要素生产率（Total Factor Productivity，简称TFP）是指在考虑全部投入要素（包括劳动、资本、能源、土地等）的条件下，全面反映经济发展过程中总投入转化为产出的效率，是一个国家（区域）经济发展质量、管理能力和效率的综合体现。全要素生产率增长是剔除资本、劳动等投入要素作用外其他所有因素所带来的产出增长率，其通常归因于科技进步和技术效率改进，是判断经济增长质量和增长潜力的主要指标，众多学者、机构都对其进行过测算与分析。

综观TFP 的研究文献，测算方法大致可以分为两类，即生产函数法和指数法。由于生产函数法会受到生产函数形式设定和模型参数估计局限性的影响，指数法得到更为普遍的应用，即通过计算TFP指数反映TFP 增长，进而利用指数分解探究TFP 变动的构成要素。在全要素生产率增长的各种测算中，针对同一对象的测算结果存在较大差异，测度方法也容易被误用、滥用。因此，我们有必要探究各类全要素生产率指数方法的来龙去脉，以便采用恰当的方法测算全要素生产率增长。

测度TFP 增长的指数方法多种多样，既有比率方法，又有差异方法；既有基于数据包络分析（Data Envelopment Analysis，简称DEA）的方法，也有基于随机前沿分析（Stochastic Frontier Analysis，简称SFA）的方法；既有只考虑期望产出的方法，也有将非期望产出纳入测算框架的方法；既有当期DEA 指数方法，也有序列DEA、窗口DEA、全局DEA、共同前沿DEA、两期DEA 指数等方法。在TFP 指数分解方面，自Nishimizu 和Page（1982）[1]提出动态分解方法以来，学者们相继给出TFP 指数的各种乘法、加法分解形式以及不同分解子项。正是因为TFP 指数测算方法众多，方法选择存在较大空间，一些研究者没能充分考虑方法的适用条件以及方法之间的逻辑关系，导致研究结论出现明显偏差。

鉴于此，为了准确测算全要素生产率增长，探究TFP 变动的动力来源，本文对TFP 指数的测算及分解方法进行了系统解析与比较。首先，本文基于数据包络分析（DEA）和随机前沿分析（SFA）的视角，全面梳理TFP 指数方法的原理、优缺点、适用性及分解方式。其次，本文对各种方法进行归类比较，以理清各类TFP 指数之间的逻辑联系和演进脉络。再次，本文对未来的重点研究方向进行展望，以期提高全要素生产率增长测算的前沿性、准确性。

本文的创新之处在于：（1）从基于DEA 的指数方法和基于SFA 的指数方法两个角度，全面、系统地总结了测度全要素生产率增长的指数方法；（2）从投入产出要素、生产前沿面构建、效率测度方法、指数（指标）方法及其分解角度五个方面，梳理了各类基于DEA 的TFP 指数的演进脉络及内在联系；（3）从同一生产前沿面和不同生产前沿面的角度，详细进行了各类全要素生产率指数性质及特点的比较分析。

二、基于DEA 的全要素生产率指数

数据包络分析（DEA）是在运筹学家Charnes 等（1978）[2]评价决策单元相对效率的基础上发展起来的系统分析方法，即通过保持决策单元的投入或产出不变，利用线性规划和对偶原理确定生产前沿面，比较决策单元偏离生产前沿面的程度，以确定其相对有效性。DEA 的基本模型是CCR 模型（Charnes et al.，1978）[2]，因其是基于规模报酬不变的假设，故又被称为规模报酬不变（CRS）模型。将CCR 模型放松规模报酬不变的假设，即是BCC 模型（Banker et al.，1984）[3]，也称为规模报酬可变（VRS）模型。传统的DEA 模型只能对截面数据进行效率分析，而生产率指数（如Malmquist 指数）则可以对面板数据进行生产率分析。因此，DEA 模型若与生产率指数有效结合，即可测度全要素生产率的变动，并分解变动的来源构成。本文将基于DEA 模型框架，按照全要素生产率指数的演进脉络进行分析。

（一）基于当期DEA 的全要素生产率指数

1.Malmquist 生产率指数。Malmquist 指数最初是由瑞典经济学家和统计学家Sten Malmquist 于1953年提出的，即利用缩放因子之比构造消费数量指数（Malmquist，1953）[4]。受Malmquist 消费指数的启发，Caves 等（1982）[5]利用距离函数构造出Malmquist 指数，并用于生产率增长分析。1994 年，Färe、Grosskopf、Norris 和Zhang（以下简称FGNZ）把DEA 与非参数线性规划法结合起来度量距离函数，将Malmquist 生产率指数（以下简称M 指数） 定义为相邻两期Malmquist 指数的几何平均数（FGNZ，1994）[6]。其后，该指数在全要素生产率增长测算中得到了广泛应用（杨世迪等，2021）[7]。

基于当期DEA 模型测算M 指数，需要先计算投入或产出的距离函数，而距离函数是建立在生产可能性集之上的。经验研究往往是根据观察到的决策单元（DMU）生成生产可能性集，即先构造t 期规模报酬不变（CRS）的生产可能性集，加上约束条件后得到t 期规模报酬可变（VRS）的生产可能性集。①根据基于产出的线性规划计算距离函数，将距离函数值代入M 指数表达式，研究者就可测算当期DEA的M 指数。

M 指数的测算是基础，而要探寻全要素生产率变动的潜在来源，还需要对M 指数进行适当分解。Nishimizu 和Page（1982）[1]最先进行了全要素生产率的动态分解，包括测度相邻两期技术前沿移动的技术变化（TC）和代表相邻时期决策单元至有效生产前沿面追赶程度的技术效率变化（TEC），即利用“创新”和“追赶”分析全要素生产率增长的来源。在此基础上，FGNZ（1994）[6]进一步使用非参数线性规划技术估计距离函数，用距离函数表示技术变化（TC）和技术效率变化（TEC）。Färe 等（1994）[8]指出，技术效率变化在规模报酬不变的情况下，可进一步分解为纯技术效率变化（PTEC）和规模效率变化（SEC）。由此，FGNZ 将生产率增长分解为技术变化（TC）、纯技术效率变化（PEC）和规模效率变化（SEC）。此后，Ray和Desli（以下简称RD）在CRS 下将M 指数分解为VRS 下的M 指数和规模变化，即技术变化（TCV）、纯技术效率变化（PTEC）和规模变化（SC）（Ray and Desli，1997）[9]。Simar 等（1998）[10]、Zofio 等（1998）[11]将RD 中的规模变化又分解为规模效率变化（SEC）和规模技术变化（STC），即将M 指数进一步分解为技术变化、纯技术效率变化、规模效率变化和规模技术变化。②

尽管各种分解方式存在一定的差异，但其皆具有合理性，实际应用中的选择取决于待解决问题的要求以及所能收集到的数据等现实条件。当期DEA模型与M 指数相结合可应用于TFP 增长测算，其既能避开设定生产函数具体形式和选择随机变量分布假设等问题，也不存在价格体系的影响，TFP 指数可以分解为技术效率变化和技术进步等因素，从而提供更全面的TFP 增长信息，且其适用于面板数据分析，由此成为测算TFP 增长的常用方法。

用M 指数测算全要素生产率增长虽然有着很多优点，但其也隐含一些缺陷。首先，使用一般技术进行参数估计时构成M 指数的一些距离函数可能是不确定的，Briec 和Kerstens（2009）[12]证明了基于当期DEA 计算M 指数可能会出现无可行解的问题。其次，技术的规模报酬性质对M 指数的测算与分解是非常重要的，规模报酬可变（VRS）情况下的Malmquist 指数并不能准确衡量生产率变化，同时，规模效率变化的分解也存在不一致性（Ray and Desli，1997）[9]。只有在技术呈规模报酬不变（CRS）时，M 指数的测算与分解才是恰当的，此时TFP 变化仅包含技术变化和技术效率变化两个来源。再次，Bjurek（1996）[13]认为，M 指数的角度选择较为随意，分解过程忽略了规模混合效率，因而分解是不完整的。O'Donnell（2012）[14]认为，投入和产出导向的M指数不具有乘法完备性，通常不能准确测度全要素生产率的变化。Coelli 等（2005）[15]指出，M 指数不满足跨期比较时尤为重要的传递性，无法进行多期或多边比较。③

2.Malmquist-Luenberger 生产率指数。M 指数是基于Shepard 距离函数计算的，其存在一个明显缺陷，即在度量全要素生产率增长的过程中仅关注期望产出而忽视了非期望产出的影响。为了弥补这一缺陷，基于方向性距离函数（Directional Distance Function，简称DDF）的Malmquist-Luenberger 生产率指数应运而生。

Pittman（1983）[16]首次尝试在生产率测算中引入非期望产出，但将环境因素纳入生产率分析框架通常会面临以下问题：（1）如何针对期望产出和非期望产出的联合生产问题进行建模，即受技术因素的制约，扩大期望产出的同时非期望产出也会增加；（2）如何将非期望产出的减少作为一种效率提升纳入整体分析框架，这其中还存在技术障碍（张少华和蒋伟杰，2014）[17]。为了解决以上问题，Chung 等（1997）[18]将一种方向性距离函数引入生产率测算框架，并以此为基础构建了Malmquist-Luenberger 生产率指数（以下简称ML 指数）。

ML 指数与M 指数的主要区别在于前者引入方向向量且考虑非期望产出，因两者的分解思路大致相同，此处不再详述。

3.Luenberger 生产率指标。无论是M 指数还是ML 指数，其均是基于比率的测算方法，适合于考察全要素生产率的变化情况，而对变量的“差值”难以反映（董敏杰等，2012）[19]，而且当一个或多个变量等于或接近零时，基于比率的生产率指数难以确定（Boussemart et al.，2003）[20]。因此，有学者提出应该考虑基于差异的生产率指标。④

M 指数和ML 指数测算均是基于径向距离函数，要求投入产出同比例扩张或缩减，而在存在非零松弛时，这种径向方法往往会使生产率测算结果出现偏误。因此，有学者提出可以采用一种非径向（Non-radial）、非角度（Non-oriented）的非参数DEA方法——SBM（Slack-based Measure）方向性距离函数以及相应的Luenberger 生产率指标（以下简称L指标），这既可以解决因未考虑松弛变量而高估评价对象效率的问题，也可以避免出现因不能同时考虑投入和产出而导致生产率失真的情况，以及因生产函数形式误设造成的生产率测算偏差。然而，Zhou等（2012）[21]认为，上述SBM 方法虽然可用于计算基于方向松弛的无效率度量，但其并没有正式定义函数本身，故采用与DDF 所遵循的效率度量公理化方法更为一致且具有理想数学性质的非径向距离函数（Non-Radial Directional Distance Function，简 称NDDF）代替SBM 方法，可以避免径向距离函数存在的问题。随后，Fujii 等（2014）[22]引入了基于NDDF 构建的L 指标。

L 指标和M 指数一样可以基于技术角度进行分解，其区别在于形式上是加法而不是乘法。刘瑞翔和安同良（2012）[23]针对SBM 方向性距离函数和L 指标的特点提出一种基于要素角度的分解方法，即在计算全要素生产率的同时考虑单个投入要素生产率的变化情况，以确定某一种投入（如资本、劳动等）的减少或产出的增加对全要素生产率提升的贡献度。可见，L 指标既可以基于技术角度进行分解，又可以基于要素角度进行分解。

由于ML 指数与L 指标均是基于当期DEA 进行测算的，两者不仅拥有M 指数所具有的理想性质，还能将非期望产出纳入测算框架，但其与M 指数一样仍存在当期DEA 固有的缺点，故全要素生产率指数仍有待进一步的改进。

（二）全要素生产率指数的拓展

DEA 是一种确定性生产前沿方法，即根据决策单元的投入和产出数据构建生产前沿面，除了当期DEA 外，其还包括序列DEA 等形式。基于当期DEA的全要素生产率指数虽然相对于传统的Fisher 指数、Törnqvist 指数具有不需设定生产函数形式、不需提供价格信息等优点，但其也隐含一些不足之处，如不具备传递性、不能对不同技术下的多群体进行生产率测算等。因此，利用序列DEA、窗口DEA、全局DEA、两期DEA、共同前沿DEA 构建生产前沿面，可以实现对M 指数、ML 指数及L 指标的拓展。

1.基于序列DEA 的全要素生产率指数。

（1）Sequential -Malmquist 生 产 率 指 数。Shestalova（2003）[24]提出基于序列DEA 计算的Sequential-Malmquist 生产率指数（以下简称SM 指数），即以DMU 当期及前期观测值确定的生产技术集构造最佳生产技术前沿面。SM 指数的分解与M指数分解的思路类似，其区别仅在于生产前沿面不同。基于序列DEA 计算SM 指数时，距离函数可以通过求解DMU 序列DEA 问题得到。

（2）Sequential-Malmquist-Luenberger 生产率指数。为了避免以当期DEA 测算的ML 指数在动态分析中出现技术退步的情形，Oh 和Heshmati（2010）[25]结合序列生产可能集和方向距离函数处理环境污染变量的方法，提出Sequential-Malmquist-luenberger指数方法（以下简称SML 指数）。应当看到，如果非期望产出不包含在SML 指数中，SML 指数就相当于SM 指数。因此，SML 指数的分解框架与线性规划结合了ML 指数和SM 指数的特点，既考虑了当期及前期的观测值，又兼顾了非期望产出。

（3）Sequential-Luenberger 生产率指标。基于序列SBM 方向性距离函数的生产边界涵盖了过去时期的样本信息，能够避免全要素生产率增长测算中出现的虚假技术退步，由此构建的Sequential-Luenberger 生产率指标（以下简称SL 指标）表达式、计算距离函数的线性规划及分解框架均与L 指数类似（李兰冰和刘秉镰，2015）[26]。其区别在于，前者是基于序列生产前沿，后者是基于当期生产前沿。

综上，基于序列DEA 计算全要素生产率指数能够满足“过去掌握的技术不会遗忘”的假定，避免出现虚假的技术退步以及由此引致的技术效率“被动”提高等不合理现象，同时有利于减少混合期线性规划无可行解的情形，但其并不能彻底解决无可行解问题。此外，序列DEA 方法可以产生一个更稳定的边界，其对样本中特定的观察值存在与否不太敏感，这就使测算结果更为可信。然而，基于序列DEA 不同时期的生产前沿面构建方法往往不能保持一致，第一期生产前沿面的构建方法等同于当期DEA 方法，最后一期生产前沿面的构建方法等同于全局DEA 方法，这使得生产前沿面的构建标准前后不完全统一。

2.基于全局DEA 的全要素生产率指数。

（1）Global-Malmquist 生产率指数。鉴于序列DEA 假定不存在某一观测期的效率优于其他时期，一些研究者将求解混合时期距离函数出现无可行解的情况视为技术有效，但这种处理并不完全合理。针对这一问题，Pastor 和Lovell（2005）[27]提出通过构建由所有DMU 的所有时期数据形成的生产技术集作为共同生产前沿面，进而计算Global-Malmquist 生产率指数（以下简称GM 指数）。基于全局DEA 计算GM 指数时，距离函数可以通过求解全局DEA 模型得到。Pastor 和Lovell（2005）[27]给出了全局基准技术下的GM 指数分解方法，即将GM 指数分解为全局技术变化（BPC）和技术效率变化（TEC）。

综上，采用FGNZ（1994）分解方法可以将GM 指数分解为全局技术变化（BPC）、纯技术效率变化（PTEC）和规模效率变化（SEC），采用RD（1997）分解方法可以将GM 指数分解为全局技术变化（BPCV）、全局纯效率变化（PTEC）和全局规模变化（SC），采用SW（1998）和ZL（1999）的分解方法可以将GM 指数分解为全局技术变化（BPC）、纯技术效率变化（PTEC）、规模效率变化（SEC）和规模技术变化（STC）。因此，对比GM 指数和M 指数的分解框架可知，它们虽然存在一个共同的效率变化部分，但技术变化和规模变化部分有所不同，全局技术变化反映了当期生产可能性集与全局生产可能性集的最佳技术前沿差距的变化，而基于当期前沿的技术变化反映的是相邻两期技术前沿的变化。

（2）Global-Malmquist-Luenberger 生产率指数。与M 指数类似，ML 生产率指数通常也是采用两个当期ML 指数几何平均的形式。鉴于其无法循环累乘，不具有传递性，只能比较临近时间段短期变动的生产效率值，无法呈现生产率的长期增长趋势，而且混合方向性距离函数容易导致线性规划无可行解，Oh（2010）[28]将Global-Malmquist 生产率概念与方向性距离函数相结合，构建了Global-Malmquist-Luenberger 生产率指数（以下简称GML 指数）。GML指数在绿色全要素生产率增长测度层面具有较大优势，实践应用也较为广泛（余奕杉和卫平，2021；郭海红和刘新民，2021；汪克亮等，2021；李静和沈伟，2012）[29-32]。基于全局DEA 计算的GML 指数与基于当期DEA 计算的ML 指数的区别在于，前者构建生产前沿面时包含了所有时期的观测值，而基于全局DEA 计算的GML 指数与基于全局DEA 计算的GM指数的区别在于，前者考虑了非期望产出。

（3）Global-Luenberger 生产率指标。利用当期DEA 计算L 指标时，由于样本点并不参与技术边界的构建，无可行解的情况是经常存在的，这有可能导致生产率增长测算出现偏差。刘瑞翔和安同良（2012）[23]提出了Global-Luenberger 生产率指标（以下简称GL 指标），其计算表达式及相应的线性规划是GML 指数与L 指标的结合，与GML 指数的区别在于形式上是差异指标，与L 指标的区别在于其考虑了所有时期的观测值。GL 指标同样可以基于技术和要素的角度进行分解，基于技术角度的分解框架类似于GM 指数，区别在于其表现为加法形式，而基于要素角度的分解框架类似于L 指标，区别在于生产前沿不同。

综上，全局DEA 是以所有时期的投入产出数据构造不同时期的共同参照技术集，将所有观测值在统一边界下进行效率评价，根据相邻时期观测值技术效率的差异就可得到全局全要素生产率指数。这种生产率评价方法的优点在于，待评估的样本点必然包含在技术边界之内，从而有效避免了无可行解的问题。同时，全局全要素生产率指数是一种单一度量，不需要采用相邻时期的几何平均值，既能满足可传递性和循环性的要求，又和序列全要素生产率指数一样排除了技术倒退的情况，且适用于不平衡面板数据分析（Asmild，2007）[33]。全局全要素生产率指数的缺点在于，根据样本的所有观测值确定生产前沿面对向数据集中添加额外数据（决策单元或时间段）比较敏感，一旦加入新数据就需要重新计算，其结果可能会发生较大变化，故全局全要素生产率指数会受到研究期限的限制，测算结果也缺乏稳健性。

3.基于窗口DEA 的全要素生产率指数。传统的DEA 多用于同一时期多个DMU 的效率评价，针对其忽略时间因素的缺陷，Charnes 和Cooper（1984）[34]采用类似平滑系数的方法进行改进，提出窗口DEA（Window-DEA）方法。窗口DEA 的基本思想是，按照一定宽度将研究期限划分为多个窗口，各窗口下同一DMU 被视为多个不同的DMU，这样就可以有效扩充DMU 数量，改进DMU 数量较少或指标数量较多的情况下出现多个DMU 效率为1 以及相对效率辨识度不高等弊端（吴浩然等，2017）[35]。窗口DEA 采用窗口期内的数据构建生产前沿面，随着老数据从窗口中退出，新数据不断进入窗口，避免了当期DEA 可能出现的技术退步问题，有利于构建光滑的生产前沿面，从而减少非可行解的情形（周五七，2015）[36]。窗口DEA 的主要缺点是，窗口宽度的设定没有统一标准，一般是根据研究对象和研究期限来设置。Färe 等（2007）[37]提出，基于产出距离函数可以构造Windows-Malmquist 生产率指数（以下简称WM 指数），其可分解为技术变化和技术效率变化。

由于窗口DEA 的窗宽选择存在模糊性，其应用受到了一定的限制。部分学者在WM 指数的基础上提出固定WM 指数，但其也存在一定的缺陷，目前还没有基于窗口DEA 对ML 指数和L 指标进行的拓展。

4.基于两期DEA 的全要素生产率指数。

（1）Biennial-Malmquist 生产率指数。针对当期DEA-M 指数可能出现无可行解的问题，Shestalova（2003）[24]、Pastor 等（2005）[27]、Färe 等（2007）[37]分别提出SM 指数、GM 指数、WM 指数。这些指数虽然在处理无可行解问题的同时可以排除技术退步的识别，但容易导致计算结果不稳定。因此，Pastor 等（2011）[38]基于两期生产可能性集，提出一个新的指数，即Biennial-Malmquist 生产率指数（以下简称BM 指数）。BM 指数不仅可以避免无可行解的问题，而且可以衡量技术变动，在数据集增加新的时间段时保持先前计算的生产率变化，但其缺点是不满足循环性和传递性要求。BM 指数的分解框架与GM 指数类似，区别仅在于生产前沿面不同。

（2）Biennial-Malmquist-Luenberger 生 产 率 指数。ML 指数和M 指数一样不能避免线性规划无可行解的问题，为了弥补SML 指数和GML 指数的不足，王兵等（2013）[39]借鉴BM 指数的原理，结合非期望产出，在加入方向性距离函数的基础上构造了Biennial-Malmquist-Luenberger 生产率指数（以下简称BML 指数），并测算了2003—2010 年考虑非期望产出的中国工业行业的能源效率。BML 指数的表达式、分解框架、线性规划均与BM 指数类似。

（3）Biennial-Luenberger 生产率指标。为了弥补BL 指标和GL 指标的不足，Liu 等（2020）[40]引入基于两期DEA 计算的Biennial-Luenberger 生产率指标（以下简称BL 指标）。BL 指标的表达式与BM 指数的区别在于形式为减法而不是除法，分解框架与BM 指数的区别在于其是加法形式而不是乘法形式，其线性规划则需结合BM 指数与L 指标的线性规划形式加以计算。

综上，基于两期DEA 的全要素生产率指数虽然可以弥补序列、窗口和全局全要素生产率指数在处理无可行解问题和排除技术退步情形方面的缺陷，衡量距离函数或方向性距离函数计算过程中存在的技术退步，但其不具备全局全要素生产率指数的传递性和循环性等优点，亦不能和窗口全要素生产率指数一样解决小样本问题。

5.基于共同前沿DEA 的全要素生产率指数。

（1）Metafrontier-Malmquist 生产率指数。生产率测算往往假设所有评价对象具有相同的技术水平即处于共同生产前沿下，而现实中存在的内部特性或外部环境差异使得评价对象具有异质性。为了解决评价多群体效率和生产率问题，Hayami（1969）[41]提出共同前沿模型，共同前沿被认为是所有可能来自异质单元前沿的包络（Wang et al.，2017）[42]。在既有研究的基础上，Battese 等（2004）[43]提出采用技术落差比例（TGR）衡量不同技术条件下单一群组在整个产业潜在效率中的地位。至此，共同前沿模型基本形成。⑤Rambaldi 等（2007）[44]用距离函数表示共同前沿生产函数，采用DEA 方法在共同生产可能性集下构建共同前沿的Malmquist 生产率指数。其后，Oh 和Lee（2009）[45]在衡量1970—2000 年58 个国家的生产率变化时构建了全局Metafrontier-Malmquist 生产率指数（以下简称MM 指数）。因此，比较不同技术条件下群体的生产率变化时可计算MM 指数，而不是传统的M 指数。此外，与GM 指数类似，MM 指数同样具有传递性、循环性等优点。共同前沿方法的核心思想是将各决策单元按生产技术条件划分为不同群组，针对全体和各群组分别构建生产前沿面，以考虑不同技术条件下群组之间的技术差异性对群组生产率的影响。为了定义和分解这种影响，当期参考技术、跨期参考技术和共同参考技术需要区分出来。

MM 指数的分解与SM 指数、GM 指数存在一定的差异，即其可以分解为群组技术效率变化（GTEC）、群组技术变化（GBPC）和技术落差比例变化（TGC）。其中，群组技术效率变化（GTEC）反映了统一生产技术下相邻两时期至当期生产前沿的追赶程度，群组技术变化（GBPC）测度了统一生产技术下当期生产可能性集合与跨期生产可能性集合的最佳技术前沿差距的变化，而技术落差比例变化（TGC）反映了相邻两时期跨期参考技术边界与共同参考技术边界的最优技术落差比例的变化，其可进一步分解为纯技术追赶（PTCU）和潜在技术相对变动（PTRC）。

（2）Metafrontier-Malmquist-Luenberger 生产率指数。ML 指数在评价生产率变化时是无法区分决策单元所采用的各种技术的，所以技术存在异质性时需要引入共同前沿方法。在MM 指数的基础上，Oh（2010）[46]提出了Metafrontier-Malmquist-Luenberger生产率指数（以下简称MML 指数）。基于共同前沿DEA 计算MML 指数，既考虑了非期望产出，又包含了所有群组、所有时期的观测值。

（3）Metafrontier-Luenberger 生产率指标。为了同时处理不良产出、非零松弛变量和跨群体异质性等问题，Yu 等（2014）[47]提出了Metafrontier-Luenberger生产率指标（以下简称MFL 指标）及具体的分解方式，并运用其考察了鄱阳湖生态经济区建立对区域环境全要素生产率增长的影响效应。MFL 指标是基于共同前沿进行测算，计算表达式、线性规划及分解框架均是MML 指数与L 指标的结合，其与MML 指数的区别在于形式上为加法形式，与L 指标的区别在于考虑了所有群体、所有时期的观测值。

综上，共同前沿DEA 是基于所有群体、所有时期的观测值构建生产前沿面，涉及群组的当期、跨期和全局参考技术。因此，基于共同前沿DEA 的全要素生产率指数不仅具有全局指数的所有优点，还有效解决了不同技术条件下的多群体效率、生产率评价问题。

（三）全要素生产率指数的新发展

基于当期DEA 的传统全要素生产率指数主要包括M 指数、ML 指数和L 指标，序列DEA、窗口DEA、全局DEA、两期DEA、共同前沿DEA 等则是对生产前沿面构建方法进行的拓展，可以解决传统全要素生产率不具有循环性、可能面临虚假技术回归和线性规划无可行解、未将群体异质性纳入模型等问题。然而，传统全要素生产率指数仍存在一些悬而未决的问题，如角度选择较为随意、分解中遗漏分解项导致分解不完整、仅考虑决策单元个体层面的生产绩效而忽略群组总体层面的生产率等。为了解决这些问题，学者们又提出一些新的指数。

1.Malmquist 指数的改进——HMB 指数。M 指数的构造是从投入或产出角度来定义，但基于两个角度计算得到的结果有所不同，这就导致M 指数存在投入和产出角度选择的随意性以及计算结果不可比的弊端。为了克服上述缺陷，Bjurek（1996）[13]在Hicks（1961）[48]和Moorsteen（1961）[49]研究的基础上，采用产出角度与投入角度M 指数的比率作为一个可行的解决办法，从而得到Hicks-Moorsteen-Bjurek 生产率指数（以下简称HMB 指数）。

O′Donnell（2008）[50]将HMB 指数分解为技术进步和TFP 效率变化（TFPEC）。TFPE 又有三种分解方式，第一种方式是将TFPEC 分解为技术变化、技术效率变化、规模效率变化、残余混合效率变化，第二种方式是将TFPEC 分解为技术变化、技术效率变化、混合效率变化、残余规模效率变化，第三种方式是将TFPEC 分解为技术变化、技术效率变化、规模混合效率变化。其中，投入导向和产出导向分解出的残余混合效率变化（RMEC）是投入和产出配置同时发生变化时得到的分解变量，可以不作投入和产出导向的区分，其余分解项则均有投入导向和产出导向两种方式，即TFPE 在投入导向和产出导向上分别有三种不同的分解方式。

HMB 指数相较于M 指数具有一些明显的优势：HMB 指数同时考虑了投入和产出方向，不需要在投入与产出方向之间进行选择；在CRS 和VRS技术条件下，HMB 指数保有全要素生产率的特性，投入和产出的强可处置性使其满足决定性公理，避免了无可行解的问题（Briec and Kerstens，2011）[51]；HMB 指数具有乘法完备性，可以进行完全分解（Laurenceson and O'Donnell，2014）[52]。此外，HMB 指数不需要对生产技术性质、市场结构、规模收益和价格信息等方面进行限制性假设。因此，利用HMB 指数进行的全要素生产率增长测度相较于M 指数的测算结果更为可靠。

2.Färe-Primont 生产率指数。Färe-Primont 生产率指数（以下简称FP 指数）是由O′Donnell（2014）[53]提出的，即先基于线性规划计算距离函数，再利用距离函数计算FP 指数。由于FP 指数可以表示为Färe 和Primont（1995）[54]所定义的产出指数与投入指数的比值，不需要对角度进行选择，满足包括传递性检验在内的一系列指数公理，具有乘法完备性，能够完全分解且不需要对技术、企业行为及市场结构进行任何假设，在测算全要素生产率增长及其构成要素时，FP 指数相较于M 指数和HMB 指数更为可靠。此外，FP 指数与HMB 指数具有相同的分解框架。

3.Luenberger 生产率指标的改进——LHM 生产率指标。相对于M 指数而言，L 指标既同时考虑了期望产出和非期望产出，也能够从技术和要素两个角度进行分解，但L 指标和M 指数一样具有不满足乘法完备性等特性。因此，Briec 和Kerstens（2004）[55]在HMB 指数的基础上引入基于差异变化的Luenberger-Hicks-Moorsteen 生产率指标（以下简称LHM 指标），即L 产出指标与L 投入指标的差值。Barros 等（2010）[56]将LHM 指标分解为技术变化和技术效率变化，Ang 和Kerstens（2017）[57]则将其分解为技术变化、纯技术效率变化和规模效率变化。虽然LHM 指标和HMB 指标一样具有一些良好的特质，但相关的实证分析文献较少，其分解也有待进一步的完善。

4.聚合Luenberger 生产率指标。多数全要素生产率指数都注重决策单元个体层面的生产率测算及分解，而忽略了群组内所有个体在聚合层面的全要素生产率增长测算与分解。聚合概念源于德布鲁对资源利用系数的分析（Debreu，1951）[58]，用以衡量一个经济体的整体效率。Farrell（1957）[59]提出一种利用“一个行业内企业（个体层面）的绩效”衡量“一个行业（群组层面）的生产效率”的方法，以这种方式衡量的“一个行业（群组层面）的技术效率”被称为结构效率，可用基于给定价格向量的方向性距离函数表示。Zelenyuk（2006）[60]将这种结构效率的理念及测算方法与M 指数相结合构建了聚合M 指数，Färe 等（2003）[61]、Mussard 等（2006）[62]也由此构建了聚合L指标。为了发挥HMB 指数的优势，Mayer 和Zelenyuk（2014）[63]依据同样的理念构建了聚合HMB生产率指数，并进行了初步分解。然而，在实际应用中，要素的价格信息尤其是非期望产出的价格信息很难获取，故Ferrier 等（2010）[64]基于给定向量的方向距离函数进行了效率测算，并将效率进一步分解为技术效率和结构效率。Boussemart 等（2015）[65]、Shen 等（2018）[66]、Boussemart 等（2020）[67]同样是基于给定向量的方向距离函数构建了聚合Luenberger 生产率指标（以下简称聚合L 指标），并分别对中国经济区域、中国农业部门及医疗保健领域的生产率演变进行了测算，分解出结构效率变化部分。其中，Shen 等（2018）[66]、Boussemart 等（2020）[67]将结构效率变化进一步分解为衡量与最优投入或产出组合差距的混合效率变化（MIXEC）以及向最佳规模移动所实现的生产率增益的规模效率变化（SCALEEC）。

以上四个指数的计算均是基于当期DEA 计算距离函数或方向性距离函数，当然也可以基于序列DEA、窗口DEA、全局DEA、共同前沿DEA 和两期DEA 进行扩展，具体方法与SM 指数、WM 指数、GM指数、MM 指数和BM 指数类似，这里不再一一列出。

通过上述DEA 指数方法的梳理可以发现，构建测度TFP 增长的DEA 指数模型需要考虑五个方面，即投入产出要素、效率测度方法、生产前沿构建、指数（指标）形式以及指数（指标）分解方法。部分学者在开展DEA 指数的应用研究时，因理解不透彻而产生误用和滥用现象。（1）在投入产出要素方面，资源要素和非期望产出未被纳入测算框架。在实际的生产过程中，投入要素不仅包括资本和劳动投入，还应包括资源因素，且非期望产出也会伴随期望产出一同生产出来，利用M 指数度量TFP 增长时如果忽视资源因素和非期望产出的影响，就会在一定程度上造成对TFP 增长的不科学评价。（2）在生产前沿构建方面，基于当期生产前沿计算混合方向性距离函数存在潜在的线性规划无可行解问题（Briec and Kerstens，2009）[68]。针对这一问题，国内外学者选择通过改变生产前沿面的方法加以解决，拓展出序列DEA 模型、全局DEA 模型、共同前沿DEA 模型等。（3）在效率测度方法方面，距离函数和方向性距离函数存在径向或角度选择不明确的问题。径向要求投入或产出同比例增长，角度则需要满足产出不变或投入不变的假设，当存在投入过度或产出不足的情形时，径向距离函数方法就会高估决策单元的效率，而角度距离函数方法因忽视投入或产出的某一个方面使得测算结果不准确。因此，测度TFP 的DEA 指数构建需要从径向和角度的距离函数方法转向非径向和非角度的方法（如SBM 方法或非径向方向性距离函数）。（4）在指数（指标）方法选择方面，M 指数、ML 指数、L 指标未同时考虑投入与产出的变化，偏离了全要素生产率的本质内涵，因而不能准确、完整地测度全要素生产率的变化。譬如，对比EGLHM 指标和L 指标的测算结果可知，EGLHM 指标的测算结果明显大于L 指标（Kerstens et al.，2018）[69]。（5）在指数（指标）分解角度方面，采用距离函数构建的M 指数（或ML 指数）不具有可加性，其仅能基于技术角度对TFP 指数进行分解，不能反映各投入产出因素对TFP 增长的影响。因此，采用具有可加性结构的SBM-DDF 或NDDF 构建可加性TFP 指标如L 指标和EGLHM 指标测度TFP 增长是非常必要的，这样可以从技术和要素两个角度对TFP 指数进行双重分解，从而全面探究TFP 增长的潜在影响因素。

三、基于SFA 的全要素生产率指数

基于DEA 的全要素生产率增长测算与分解，均是采用线性规划的非参数方法构造生产前沿面。与之相对应，实际研究中使用随机前沿分析（SFA）构造生产前沿面也是可行的，该方法本质上是一种极大似然估计的参数方法（张少华和蒋伟杰，2016）[70]。

随机前沿分析（SFA） 是由美国的Aigner 等（1977）[71]、比利时的Meeusen 等（1977）[72]、澳大利亚的Battese 等（1977）[73]分别提出的，早期的模型只针对横截面数据进行分析，且不能处理多投入、多产出问题。Battese 和Coelli（1992）[74]将其拓展为适用于面板数据且能对前沿函数和技术无效率函数的参数进行估计的随机前沿生产函数模型。Zhou 等（2012）[21]将Shepard 距离函数与随机前沿生产函数相结合，使得SFA 模型能够同时处理多投入、多产出问题。SFA 模型的一般形式为：

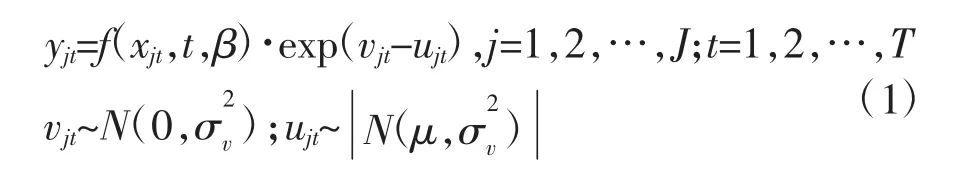
其中：yjt为第j 个决策单元（DMU）t 时期的产出，xjt为第j 个决策单元（DMU）t 时期的投入向量；t表示时间，反映技术变化；f（xjt，t，β）为特定函数形式（包括柯布道格拉斯生产函数和超越对数生产函数等）；β 表示待估计的投入向量参数；vjt表示随机统计误差，假定服从正态分布；ujt表示技术非效率所引致的误差，假定服从截断正态分布；vjt与ujt相互独立。对数形式为：

利用极大似然估计方法可以确定函数中的参数，得到每个DMU 各时期的距离函数（技术效率值）。技术效率（TE）用实际期望产出与生产前沿面产出期望的比值表示，则第j 个DMU 在t 时期的技术效率可以定义为：

若uit=0，则，该个体恰好在生产前沿面上，即处于技术有效状态；若uit＞0，则∈（0，1），该个体位于生产前沿面之下，即处于非技术效率状态。从时期t 到时期t+1，第j 个DMU 技术效率的变化按以下公式计算：

第j 个DMU 从时期t 到时期t+1 的技术变化，可以通过对随机前沿函数的参数直接求时期t 的偏导数计算得出。当技术变化非中性时，技术变化值随着投入向量的不同而有所差异，因此，相邻时期t 和时期t+1 的技术变化值应采用几何平均值，即有：

基于SFA 计算的M 指数可以表示为技术效率变化与技术变化的乘积。与DEA 相比，SFA 利用随机前沿模型将随机因素的影响分离出来，避免结果受到测量误差或其他随机性误差的冲击，能够较好地消除确定性模型产生的随机偏误所带来的影响，使结论更接近于事实。当然，SFA 也存在生产函数设定具有主观性、需要假定统计误差和技术无效率误差的分布形式等不足。既有文献主要是基于SFA计算Malmquist 指数的，而基于SFA 的ML 指数、L指标等应该成为未来全要素生产率指数的重要拓展方向。

四、全要素生产率指数的比较分析

全要素生产率指数既包括基于当期DEA 测算的M 指数、ML 指数和L 指标，以及基于序列DEA、窗口DEA、全局DEA、两期DEA 和共同前沿DEA测算的拓展指数，还包括四个改进和新发展的指数，即HMB 指数、FP 指数、LHM 指标和聚合L 指标。在对各种指数的测度与分解、优缺点进行阐述之后，本文将根据全要素生产率指数的表现形式、距离函数及生产前沿面构建方法的不同，进行指数的比较分析。

依据表1 的分类，本文从纵向（同一生产前沿面）和横向（不同生产前沿面）两个角度，对各种全要素生产率指数测算和分解中所体现出的性质及特征进行比较与解析。

表1 全要素生产率指数的分类框架

（一）同一生产前沿面的全要素生产率指数比较

全要素生产率增长测度包括基于比率的指数和基于差异的指标两种形式。在基于比率的指数中，M指数及其拓展指数（SM、WM、GM、MM、BM 指数，下同）均是基于Shepard 距离函数构建的指数，ML 指数及其拓展指数则是基于方向性距离函数构建的指数。方向性距离函数相较于Shepard 距离函数多出一个方向向量，可以同时考察投入减少和产出增加，也能兼顾期望产出和非期望产出。Shepard 距离函数和方向性距离函数均属于径向距离函数，要求投入产出同比例扩张或缩减，而基于差异的L 指标及其改进指标则是基于一种非径向、非角度的SBM 方向性距离函数构建的，它既同时考虑了期望产出的增加和非期望产出的减少，也解决了因未考虑松弛变量而高估评价对象效率的问题。

同一生产前沿面的全要素生产率指数在很多性质上（如函数形式、传递性、循环性等）呈现出一定的联系及差异。本文以基于当期DEA 构建生产前沿面的方法为例，进行了代表性指数M 指数、HMB 指数、FP 指数、ML 指数、L 指标和LHM 指标性质的对比分析，结果如表2 所示。⑥基于序列DEA、窗口DEA、全局DEA 等其他生产前沿面构建的指数具有相似的差异特征，比较分析方法也类似。

表2 同一生产前沿面的全要素生产率指数性质对比

（续表2）

表2 中的全要素生产率指数相较于Fisher 指数、Törnqvist 指数等传统生产率指数而言，其均不要求设定具体函数形式和获取要素价格信息，且适用于面板数据分析，能够用于有价值的动态趋势判断。

在仅考虑期望产出的情况下，全要素生产率增长测度可以采用M 指数、HMB 指数和FP 指数。相较于M 指数，HMB 指数和FP 指数具有以下优势：指数形式为产出量指数与投入量指数的比值，不存在角度选择问题；全要素生产率增长测算过程不受规模报酬性质的影响，具有循环性，且能够避免线性无可行解问题；HMB 指数分解不需要对技术、企业行为及市场结构等进行假定，其分解体现出乘法完备性，能够完全分解为几项因素的乘积；FP 指数可以满足开展多边比较的传递性要求。当然，在指数分解方面，M 指数与HMB 指数、FP 指数也存在一定的差异。由于技术的规模报酬性质会对M 指数产生影响，M 指数的分解还存在一定的争议，且M 指数的分解往往会忽略规模混合效率，这使得分解并不完整，而HMB 指数和FP 指数均满足乘法完备性，分解子项除了包含技术变化、技术效率变化和规模效率变化外，还考虑了残余混合效率变化、混合效率变化、残余规模效率变化和规模混合效率变化等，分解是较为完全的。

Peyrache（2014）[75]提出了反映生产率变化的原始指数——径向生产率指数（RPI），⑦其可精确分解为三个部分：技术变化（TC）、技术效率变化（TEC）和平均规模经济（径向规模变化，简称RSC），即RPI=TEC·TC·RSC。RPI 指数在一定程度上反映了M 指数与HMB 指数之间的联系，可以表示为：HMB=TEC·TC·RSC=RPI·Hom。其中，Hom 表示偏离同质性假设。事实已证明：（1）在满足CRS（技术非逆同质性）时，RPI 指数等同于M 生产率指数；（2）在技术逆同质性（VRS）条件下，RPI 指数等同于HMB 生产率指数；（3）在CRS 和技术逆同质性条件下，M 指数等同于HMB 指数。

若将非期望产出纳入全要素生产率增长测算框架，ML 指标、L 指标和LHM 指标均可同时考虑期望产出的扩张和非期望产出的缩减。相较于ML指数，L 指标和LHM 指标通常是基于SBM 方向性距离函数进行测算，考虑了松弛变量以避免高估评价对象效率的问题，而且其既可以从技术角度进行分解，也可以从要素角度进行分解，能够反映完整的全要素生产率变化情况，且能计算单个投入要素生产率的变动情况。另外，LHM 指标与L 指标的比较类似于HMB 指数与M 指数的关系，LHM 指标是在HMB 指数的基础上提出且是基于差异的指标，具有HMB 指数的所有良好特性，且满足乘法完备性，能够完全分解。

（二）不同生产前沿面的全要素生产率指数比较

全要素生产率指数的生产前沿面主要包括当期DEA、序列DEA、窗口DEA、全局DEA、两期DEA 和共同前沿DEA 等。当期DEA 是基于当期观测值构建生产前沿面，容易受到经济波动等外生性因素的影响，动态分析中可能出现虚假的技术退步。序列DEA 是基于当期及以前所有时期的观测值构建生产前沿面，能够避免技术退步和线性规划无可行解的情形，但不能彻底解决无可行解的问题。窗口DEA 是利用当期及前两期（视为一个窗口期）的观测值构建生产前沿面，是介于当期DEA 与序列DEA 之间的一种折中方法，其初衷是解决利用小样本数据构建生产前沿面时存在的DMU 数量不足问题，而随着窗口中新老数据的替换，其也能避免技术退步和无可行解的问题。全局DEA 是基于所有时期观测值构建生产前沿面，其假设前提是参考技术固定不变，故基于全局DEA 的生产率指数或指标是单一指数或指标，无需采取相邻两期指数的几何平均形式或相邻两期指标的简单平均形式，既可满足可传递性、可循环性要求，又能避免线性规划无可行解的情形，还排除了技术倒退的情况（周五七，2015）[36]。两期DEA 是基于相邻两期观测值构造生产前沿面，其可解决线性无可行解问题，能够衡量技术退步，且加入新时期的数据也不需要重新计算，与全局DEA 相比更具有稳定性，但其无法解决循环性和传递性问题。共同前沿DEA 是基于所有群体、所有时期的观测值构建生产前沿面，涉及群体的当期、跨期和全局参考技术，故基于共同前沿DEA 构建的全要素生产率指数除具备全局DEA 的所有优点外，还能比较不同技术下群体生产率的变动特征。

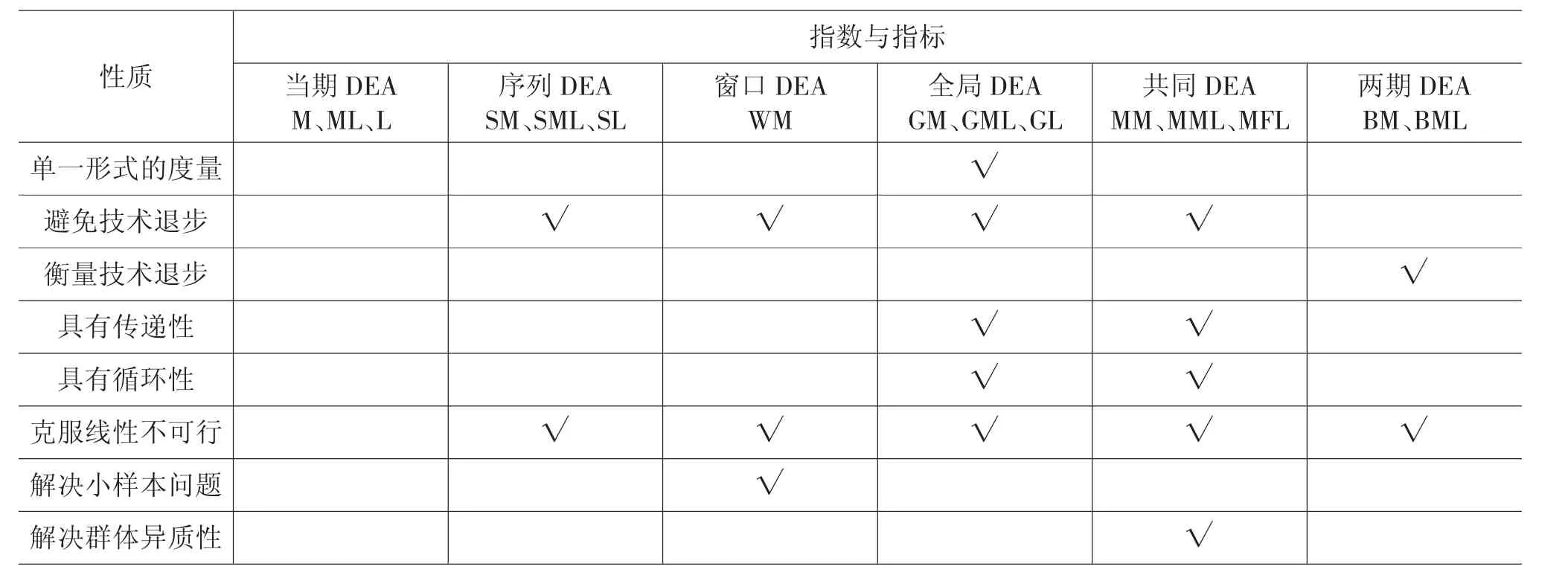
表3 不同生产前沿面的全要素生产率指数性质对比

基于不同生产前沿面的全要素生产率指数分解框架存在一定的差异：（1）当期DEA 指数和序列DEA 指数的分解框架基本相同；（2）现有文献多是将窗口DEA 指数分解为技术变化（TC）和技术效率变化（TEC）两部分；（3）全局（两期）DEA 指数的分解思路与当期DEA 指数的分解思路类似，其中，全局效率变化和全局规模变化与当期DEA 的效率变化和规模变化相同，不同的是全局（或两期）技术变化代表当期生产可能性集合与全局（两期）生产可能性集合的最佳技术前沿差距的变化，而当期DEA 的技术变化代表相邻两期技术前沿的变化；（4）基于共同前沿DEA 的指数考虑了群组的当期、跨期和全局前沿，分解项中包括反映相邻两时期至当期生产前沿追赶程度的技术效率变化（TEC）、当期生产可能性集合与跨期生产可能性集合的最佳技术前沿差距的技术变化（BPC）、相邻两时期跨期参考技术边界与共同参考技术边界的最优技术落差比例的变化（TGC），而TGC 又可进一步分解为纯技术追赶（PTCU）和潜在技术相对变动（PTRC）两项。

（三）基于DEA 与基于SFA 的全要素生产率指数比较

基于DEA 和基于SFA 的全要素生产率指数测算及分解各有其特点。一般而言，当样本数据测量误差较大或者测算结果易受随机扰动因素影响时，参数化前沿分析方法（SFA）往往优于非参数前沿分析方法（DEA），而当样本数据缺乏价格信息或者测算结果受随机扰动因素的影响较小时，采用非参数前沿分析法（DEA）则是比较恰当的。基于DEA 的全要素生产率指数结合线性规划方法计算每个决策单元（DMU）的生产率变化时，不需要设定具体的函数形式。然而，DEA 是确定性模型，无法排除随机因素的干扰，也不能进行统计检验。基于SFA 的全要素生产率指数需要为生产前沿设定具体的函数形式，对误差项的分布特征也有强假定，同时对样本容量的要求较高。但SFA 方法具有能够对模型参数及模型本身进行检验、可以分解出随机误差等优点。可见，利用基于DEA 的非参数法和基于SFA 的参数法进行全要素生产率增长的测算与分解各有优势和不足。总体来看，在现有全要素生产率指数的研究文献中，采用非参数DEA 模型进行分析的居多。对于考虑了污染排放等非期望产出约束的多投入、多产出系统，DEA 模型更能反映可持续发展的需要，其在绿色经济转型绩效评价研究中的应用也更为广泛。基于SFA 模型的全要素生产率指数分析目前主要是使用SFA-Malmquist 指数，其他类型的指数还有待进一步的拓展与改进。

五、结语及展望

全要素生产率增长测算能够在一定程度上反映经济增长的质量，解释经济增长中技术进步的贡献。因此，准确测度全要素生产率变动及其来源构成，是一个国家或地区制定经济规划、实施宏观调控、出台产业政策的重要依据。全要素生产率增长测度从最初的索洛余值法到目前普遍应用的指数法，方法变得更为精细，既能反映全要素生产率增长，又可利用指数分解反映全要素生产率变动的因素构成。

全要素生产率指数涵盖基于DEA 的非参数方法和基于SFA 的参数方法，包含仅考虑期望产出的方法和综合考虑期望产出与非期望产出的方法，从基于当期DEA 构建生产前沿面的方法到基于序列DEA、全局DEA、两期DEA 和共同前沿DEA 等构建前沿面的方法，每一种全要素生产率指数都具有自身独特的适用条件、理论基础、优缺点及分解方式，研究者在实际应用时需要结合具体的研究场景、对象特点，选择及综合使用一种或多种方法有效开展全要素生产率增长的测度及分解。

通过对全要素生产率增长测算及分解方法进行逻辑梳理和比较分析，本文发现，全要素生产率指数测算方法仍存在一定的拓展空间，有待于未来进行深入的研究。

其一，完善LHM 指标的分解方法及子项构成。既有文献使用M 指数、ML 指数和FP 指数测算全要素生产率增长的较多，指数分解也较为细致，而对于HMB 指数、L 指标和LHM 指标，理论探讨与应用分析相对较少，指数分解也不够完善，特别是LHM 指标的分解仅限于技术效率变化、技术变化和规模变化。实际上，LHM 指标是一个具有乘法完备性的差异指标，其既能像HMB 指数一样从技术角度进行完全分解，也可仿照L 指标从要素角度进行完全分解，具体的分解方法有待于进一步的完善。

其二，开展HMB 指数和LHM 指标生产前沿面构建方法的拓展研究。在既有文献中，M 指数的改进（HMB 指数）和L 指标的改进（LHM 指标）均是基于当期生产前沿进行全要素生产率指数的测算与分解。其实，类似于M 指数和L 指标，HMB 指数和LHM 指标也可拓展为基于序列DEA、窗口DEA、全局DEA、两期DEA 和共同前沿DEA 构造生产前沿面，从而显示出其可避免虚假技术退步、克服线性规划无可行解的缺陷、解决群体异质性问题等方面的良好性质。

其三，加强基于SFA 的全要素生产率指数方法的创新研究。目前基于DEA 非参数方法进行的全要素生产率指数测算及分解研究较为丰富，而基于SFA 的参数方法仅限于Malmquist 指数的测算与分解。Zhou 等（2012）[21]将Shepard 距离函数与SFA 结合起来，使得SFA 模型能够同时处理多投入、多产出问题。未来的研究可以进一步尝试基于SFA 方法对ML 指数、L 指标及拓展指数进行测算和分解，并与DEA 方法的测算及分解结果进行比较分析，以得到更为全面、客观的研究结论。

其四，强化基于窗口DEA 构建生产前沿面的研究。Färe 等（2007）[37]提出了WM 指数并进行了分解，但因存在窗口选择等问题，WM 指数的使用受到限制。李谷成等（2013）[76]借鉴固定基期Malmquist 指数的思路，构建了基于固定窗口（Fixed-Window）的Malmquist 指数（简称FWM 指数），以解决技术退步和无可行解问题，有效避免了窗口选择标准模糊不清的问题。但FWM 指数只是回避了生产率指数测算时的窗口选择难题，指数分解还是需要选择合适的窗口。因此，未来应以此为基础对窗口DEA 全要素生产率指数方法进行更深入的研究，彻底解决全要素生产率指数测算与分解的窗口选择问题。

其五，加强最新DEA 模型与已有生产率指数的结合研究。目前的全要素生产率指数研究多是将DF-DEA 模型与M 指数系列及FP 指数相结合，将DDF-DEA 模型与ML 指数系列相结合，将SBMDEA 模型与L 指标系列相结合。其实，DDF-DEA 模型和SBM- DEA 模型也可以与M 指数系列及FP 指数相结合，以测算考虑非期望产出的全要素生产率增长。此外，后续的研究应将兼具径向和非径向特征的EBM-DEA、超效率DEA、环境RAM-DEA（Sueyoshi and Goto，2011）[77]、Bootstrap-DEA、网络DEA、SBM 网络DEA（Tone and Tsutsui，2009）[78]等模型与已有的各类生产率指数相结合，开展全要素生产率增长测度与分解方法的创新性研究，其中一个值得重点关注的领域是将非期望产出纳入全要素生产率增长测算框架的绿色全要素生产率指数的测算与分解。

注释：

①假设存在J 个决策单元（DMU），每个决策单元在T 期使用N 种投入，得到M 种产出，则第j 个DMU 在t 时期的投入产出向量为：。其中，为t 时期研究的第j 个DMU 的第n 种投入为t 时期研究的第j 个DMU 的第m 种产出。后文所有的决策单元假设均相同，不再进行说明。

②规模技术变化（STC）表示CRS 下技术变化和VRS 下技术变化的比率。

③传递性意味着对两个对象/时期生产率的直接比较将产生与通过第三个对象/时期间接比较相同的生产率变化估计，同一性公理意味着两个对象使用相同的投入得到相同的产出，指数值为1。

④Diewert（2005）[79]从检验和经济角度对指数理论的比率和差异方法进行了比较，并称基于比率的生产率度量为“指数”，称基于差异的生产率度量为“指标”。

⑤共同边界方法首先是构建群组边界（Group Frontier），对群组内部的对象进行效率评价，然后在群组边界的基础上构建共同边界，评价对象在群组边界下的技术效率与共同边界下的技术效率的比值被定义为TGR。

⑥本文将HMB 指数、FP 指数和LHM 指标看作是基于当期DEA 计算得到。

⑦该生产率指数由于是利用沿着预先指定的投入产出射线的距离函数变化来定义，其通常被认为是径向生产率指数（RPI）。