基于智能手机的均质圆弧微振动研究

杨祎图，邓招华，杨 琴，冯 洁，刘应开*

(1.云南师范大学 物理与电子信息学院，云南 昆明 650500；2.龙陵县河头初级中学，云南 保山 678300)

微振动与一般振动相比振动幅值较小，但是对精度较高的仪器和设备的影响却不可忽略。微振动的研究是振动工程领域内较为重要的一个方面，其研究的主要目的是要进行振动控制，以满足机械生产工作时的性能指标要求[1]。微振动是一个相对的概念，不能一概而论，以工程学中的微振动问题为例，一般较大振幅的振动，如地震引起的房屋振动、较大风荷载引起的结构振动等，这些振动有可能引发结构构件的变形甚至造成破坏，而微振动一般振动水平较低，引起的结构响应处于线性弹性阶段，但会影响一些精密设备和仪器的正常工作，如地铁运行经过周边低矮建筑时，很容易引发振动，这类振动一般不足以造成破坏。从已有的文献及相关报告来看，对微振动的研究大多采用高精度光学仪器测量微振动振幅或者利用高精度传感器测量微振动振幅。工程学中微振动的研究采用激光干涉测量微振动振幅。多数研究是对微振动的振幅进行测量。然而在物理教学或习题中，对微振动研究主要体现在微振动的周期，如秋千的研究[2]，且主要集中在垂直于圆弧方向的摆动，对于沿圆弧方向的摆动则研究的不多。本文主要研究均质圆弧沿圆弧方向的一维微振动问题。考虑这一问题时，空气阻力和转轴处的摩擦对周期的影响较大。但是在摆角很小的情况下，空气阻力和转轴处的摩擦力对周期的影响极小，可以把均质圆弧的微振动看作一维的无阻尼振动。理论研究表明了：微振动周期与物体的质量、转动惯量和物体质心到转轴的距离以及当地重力加速度有关，因为微振动振幅较小，不易观察，所以用智能手机的可视化来研究这一微振动的周期，从而对这一问题进行深入的研究和讨论。

1 理论原理

将一段半径为R的均质圆弧两端用细线连接，在其圆心位置O点处固定一铁钉，使圆弧绕过O点并与弧面垂直的轴摆动，研究其微振动周期。

设l为均质圆弧质心到转轴处的距离，I为均质圆弧的转动惯量，M为转动力矩，ω为角频率。由力矩公式得

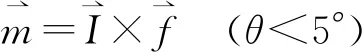
(1)

M=-mglsinθ

(2)

由转动惯量与力矩的关系得

(3)

由于均质圆弧微振，摆角很小，sinθ≈θ

(4)

(5)

(6)

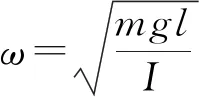
(7)

(8)

2 设计实验

2.1 实验仪器

实验仪器由均质圆弧(实验用的均质圆弧是圆的1/3)、磁性小球、铁钉、细线、智能手机组成(图1)。均质圆弧两端用细线连接，两段细线长度与圆弧半径相等，圆弧悬挂在固定好的铁钉上，用石蜡打磨细线和细线悬挂的铁钉部分，圆弧中心放置磁性小球并固定。选用316不锈钢制作均质圆弧，由于均质圆弧质量要比磁性小球质量大得多，其运动状态才符合复摆的运动，而其他材料，如塑料、铝合金，存在质量不能远大于磁性小球质量或者成本过高的问题，因而不宜采纳。

图1 实验仪器

2.2 实验方案

将智能手机安装好phyphox软件，将其放置在准备好的均质圆弧的正下方。然后让均质圆弧摆动，摆角在6°～10°。开始时圆弧的运动并非一维振动，存在着垂直圆弧方向的前后振动。经过30～40 min后，摆角小于等于5°时，圆弧的运动近似为一维振动。此时，打开手机中的phyphox软件，用内置的磁力计功能测量磁性小球的磁感应强度周期，取25个周期为一组，利用origin软件绘制周期图像，计算出均质圆弧微振动的周期数值，作误差分析。根据系统误差对理论值进行修正，最后将均质圆弧微振动周期的测量值与理论值比较，计算出相对误差，得出最后的结论。

3 实验步骤

3.1 测量均质圆弧和磁性小球的半径

3.2 测量均质圆弧和磁性小球质量

用电子秤测得均质圆弧质量为M=273.31 g，磁性小球质量为m=3.86 g。

3.3 测量当地重力加速度g

用智能手机phyphox软件界面上的“含(g)的加速度”可以直接显示出当地重力加速度g的数值。其原理是：重力传感器不会扣除手机自身的重力，所以手机静止放置时，也能测量出当地重力加速度的值[3]。取3个重力加速度数值，如图2。计算平均值，获得当地重力加速度。

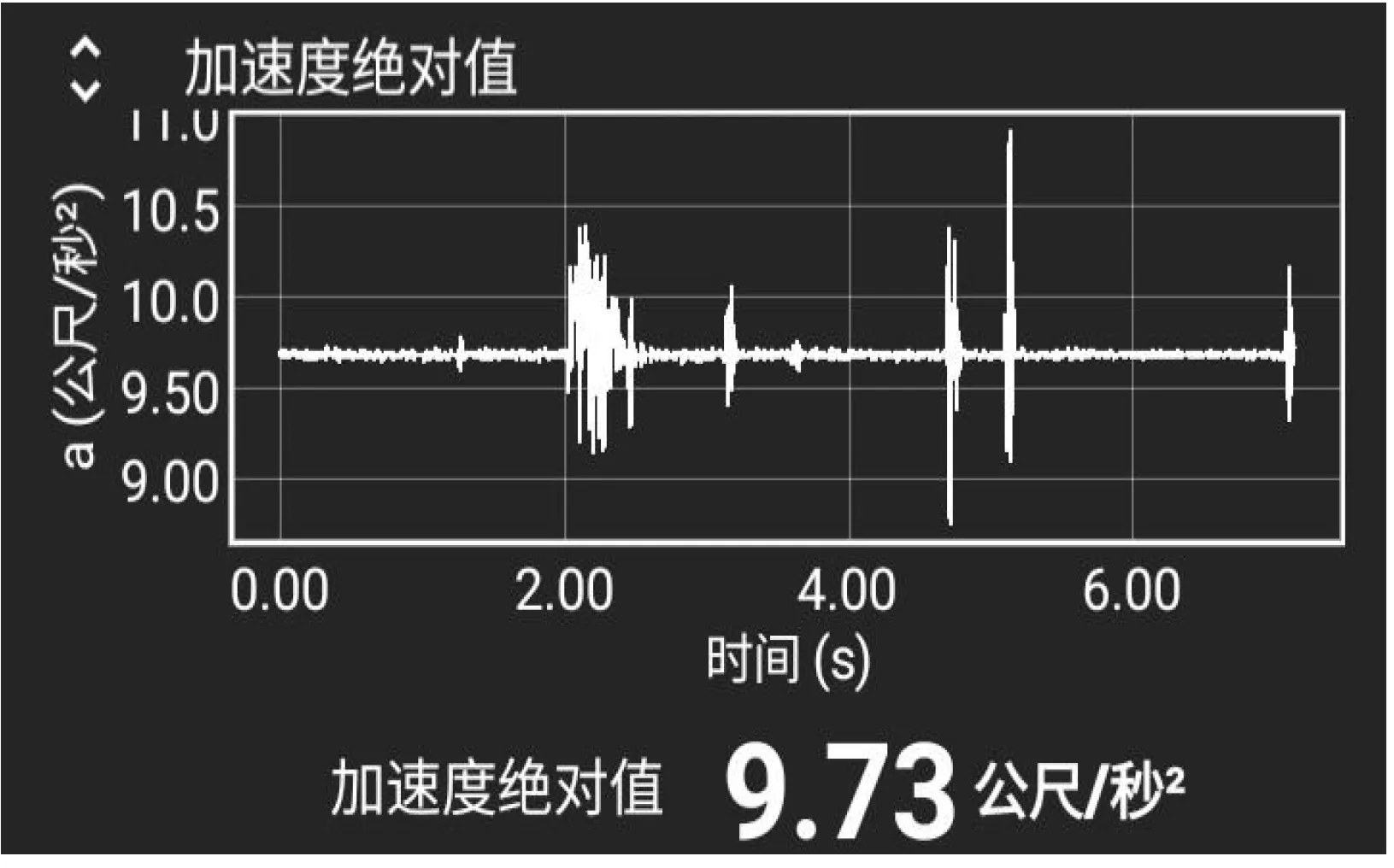
(a)

经查阅，实验室通过精确实验测量得的本地重力加速度为9.728 m/s2，与之对比，手机软件测得的本地重力加速度数值可取。

3.4 推导均质圆弧微振动周期理论式

3.4.1 均质圆弧对圆心轴的转动惯量

积分求解：

(9)

(10)

(11)

代入M得

(12)

置于均质圆弧上的磁性小球不可忽略，磁性小球对圆心轴的转动惯量为

i2=m(R1-r)2

(13)

均质圆弧和磁性小球对应同一转轴，据平行轴定理，均质圆弧和磁性小球整体的转动惯量为

(14)

3.4.2 均质圆弧质心到转轴的距离

质心定义法得

(15)

代入数据,均质圆弧质心到转轴处的距离rc1=0.299 6 m

磁性小球质心到转轴处的距离，由均匀的规则物体的质心即为几何中心直接得到rc2=R1-r

均质圆弧和磁性小球整体的质心到转轴的距离

(16)

代入数据rC=0.2992 m

将(14)式和rC代入(8)式中，得到均质圆弧微振动周期理论式

(17)

3.5 用磁力计测量磁性小球磁感应强度周期

用智能手机软件phyphox内的磁力计功能进行测量。将手机如图1水平放置，磁力计中的X轴、Y轴、Z轴分别对应手机的窄边方向、长边方向和垂直于手机平面的方向。其中Z轴的磁感应强度与时间的图像只与磁性小球竖直方向的位移有关，与运动路径无关。由于磁力计本身存在于手机自身的磁场中，对测量外部磁场均有影响，使用前需要先校准磁力计。操作步骤为：打开磁力计，点击右上方的3个小点，再点击“使用已校准的磁力计”，再开始测量[5]。测量磁场时注意将手机远离容易产生磁场的仪器和设备，如通电线圈等，以避免产生较大的测量误差。从均质圆弧摆角小于等于5°，做一维振动时打开磁力计开始记录，取Z轴图像导入数据，得到磁感应强度周期。

4 结 果

4.1 用磁性小球磁感应强度周期计算均质圆弧微振动周期

从均质圆弧摆角小于等于5°时开始计时，将智能手机phyphox软件中磁力计的测量数据导出，取25个周期为一组实验数据，使用origin软件绘制磁性小球磁感应强度周期图像，如图3，图4，图5。

时间/s

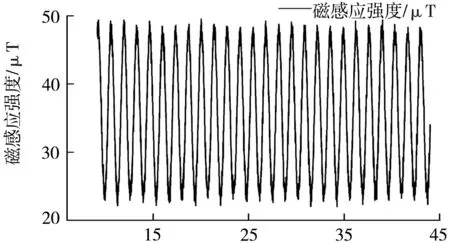
时间/s

时间/s

由于磁性小球的磁感应强度周期反映的是均质圆弧的微振动周期，计算各组实验的平均值，即磁感应强度周期图中相邻两个峰值的时间差值，就是均质圆弧微振动的周期。取多个周期为一组数据，再计算周期，可以减小取峰值时出现的随机误差，实验数据列入如表1。

表1 均质圆弧微振动周期

4.2 误差分析

4.2.1 均质圆弧微振动理论周期数值

根据公式(17)，可得均质圆弧理论值为T0=1.335 5 s

4.2.1 对均质圆弧微振动周期理论值进行修正

本实验研究产生误差主要有系统误差和随机误差，根据本实验测量均质圆弧微振动周期的理论公式和实验条件以及测量方法。重点分析均质圆弧的摆角、空气阻力和转轴处的摩擦(复合阻力)对实验结果的影响[6]。

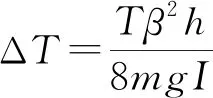
再利用origin软件拟合数据，从25个周期中取几个周期的峰值来绘拟合直线，如图6所示。

时间/s

从图6可看出，在25个周期时间范围内，磁感应强度没有发生明显的衰减，而磁感应强度周期反映了均质圆弧微振动周期，故可视为均质圆弧微振动在所取周期时间范围内的振幅没有明显的衰减，因此忽略空气阻尼和转轴处摩擦，在25个周期时间范围内，均质圆弧做无阻尼微振动。

影响均质圆弧微振动周期的因素中，摆角对周期的影响通过理论计算，在时间的测量精度10-4s就能明显得到体现。通过以上实际测量和理论计算，以及拟合图像分析，实验中影响均质圆弧微振动周期的因素是摆角大小，空气阻力和转轴处摩擦力可不予考虑。

考虑摆角的均质圆弧微振动周期修正[9]。

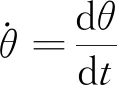
(18)

(19)

将(19)式代入(3)式得

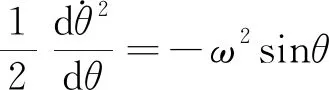
(20)

(20)式两边积分得

(21)

(22)

(23)

(24)

(25)

(26)

除去后面的高次项,得到修正后的均质圆弧微振动周期为

(27)

代入数据，计算得到均质圆弧微振动周期理论数值T=1.336 1 s。

计算相对误差

=0.11%

可见，实验中测量值接近于理论值，表明本实验的实验设计与理论推导及测量方法是可行的，是对微振动可视化的有效手段。

5 结 语

本文推导了均质圆弧和磁性小球组合系统的微振动周期公式，并设计基于智能手机的磁感应强度变化测量方法，对该系统的微振动周期进行测量。得出结果表明：均质圆弧和磁性小球组成的系统的微振动周期为1.334 6 s，修正后的理论值为T=1.336 1 s，相对误差为0.11%，二者非常接近。这一研究结果表明利用智能手机安装适当的软件，结合其内置的高精度传感器研究力学、电磁学、光学等物理问题是可行的，而且测量精度远高于实验室传统的测量方法，这对有效开展物理研究是非常有益的。