基于多层感知器神经网络的锅炉再热蒸汽温度预测

陈刚，蒲靖凡，梅海龙，虞兵，张林，石川，谭鹏

(1.国电汉川发电有限公司，湖北 孝感431616；2.华中科技大学能源与动力工程学院煤燃烧国家重点实验室，湖北 武汉430074)

0 引言

在“碳达峰，碳中和”的目标下，能源结构的转型使得我国可再生能源装机容量不断提高。然而，新能源电厂存在许多不足之处，特别是负荷难以人为控制，风力、水力、光照等受天气和季节影响较大，因此还需要与火电厂相互配合[1－2]。在这种趋势下，要解决新能源出力波动大问题，需要提高燃煤电厂的调峰调频能力，这给燃煤电厂安全运行带来挑战[3]。

再热蒸汽温度是锅炉重要运行参数之一。由于再热蒸汽压力较低，在相同的烟气传热量扰动下，再热蒸汽温度的变化幅度会比主蒸汽温度大；负荷变化会带来汽轮机高压缸排汽(也即再热器入口)温度及压力的改变，增加了再热蒸汽温度控制的难度。因此，在锅炉宽负荷灵活运行时极易导致再热蒸汽温度大幅波动。蒸汽温度过高会导致受热面超温爆管[4]，而温度过低则会影响机组经济性。当前燃煤锅炉再热蒸汽温度调节主要通过调节尾部烟道烟气挡板改变再热器侧或过热器侧烟气分配比例实现，喷水减温由于对机组发电效率有较大影响而仅作为紧急调温手段。采用烟气挡板调节再热蒸汽温度时具有时滞大、非线性强的特点，在面对快速、大范围变负荷运行时，采用传统控制方法很难及时、精准地控制烟气挡板开度。提前预估再热蒸汽温度变化趋势大大降低了再热蒸汽温度控制的难度，提升了再热蒸汽温度控制的准确性。

在大数据算法、人工智能的推动下，数据挖掘、数据预测已经运用于燃煤电厂主要运行参数的建模、预测以及控制，为再热蒸汽温度预测建模提供了手段。李胜男和金志远等利用长短时记忆神经网络(LSTM)，建立了燃煤锅炉机组的主蒸汽温度、再热汽温、炉膛出口NOx浓度、炉膛出口CO浓度的多参数协同预测模型以及再热汽温的多步预测模型[5－6]。赵佳鹏和Liu等构建了基于LS－SVM的再热蒸汽温度模型，并发现在计算时间和精度上优于BP神经网络、RBF神经网络和常规SVM算法，同时在控制优化中取得不错的效果[7－8]。华菁云提出了一种时延计算算法对时延进行评估，并基于深度神经网络和LightGBM的融合模型对再热蒸汽温度进行建模[9]。Ning等基于深度神经网络(DNN)和遗传算法(GA)，建立了再热蒸汽温度最优多步时间特征选择模型，DNN用于预测未来时间步长的再热蒸汽温度，GA用于寻找最优延迟阶数，实验表明，该方法计算的最优延迟阶数具有较高的计算精度和较低的计算开销[10]。

本文以某1 000 MW超超临界燃煤锅炉为研究对象，利用历史运行数据，建立基于多层感知器神经网络(MLP)的再热蒸汽温度预测模型，并与长短时记忆神经网络(LSTM)以及支持向量机(SVM)进行了对比。

1 研究对象与方法

1.1 研究对象

本文的研究对象为某1 000 MW超超临界燃煤锅炉。该锅炉采用单炉膛Λ型布置方式、尾部双烟道，炉膛采用内螺纹管螺旋管圈＋混合集箱＋垂直管水冷壁，中速磨正压直吹式制粉系统，配6台磨煤机(5台运行1台备用)，装设48只旋流式低NOx燃烧器，前后墙布置，对冲燃烧。过热器为辐射对流式，再热器纯对流布置。过热器采用水煤比＋两级喷水调温，再热器采用尾部烟气调节挡板＋事故喷水调温。再热器出口蒸汽温度额定值为605℃，在50%～100%B－MCR负荷范围再热器出口蒸汽温度偏差不超过±5℃。

锅炉再热蒸汽温度受很多因素影响，主要因素有高压缸排气温度、锅炉负荷、再热器侧烟气挡板开度、再热器减温水开度、锅炉送风量、受热面清洁程度、火焰中心位置等。综合考虑以上因素以及数据采集难度再热蒸汽温度预测模型的输入为:当前及过去时刻的负荷、给水流量、总燃料量、低温再热器入口烟气温度、低温过热器入口烟气温度、再热器减温水开度、再热器侧烟气挡板开度、再热器入口蒸汽压力、高温再热器入口蒸汽温度、高温再热器出口蒸汽温度。模型输出为:下一时刻的高温再热器出口蒸汽温度(即再热蒸汽温度)。共采集两个月的运行数据，数据采样周期为1 min，数据集总长度为95 041。数据集按时间步长划分后进行随机打乱，取前80%为训练集，后20%为测试集。各参数变化范围见表1。

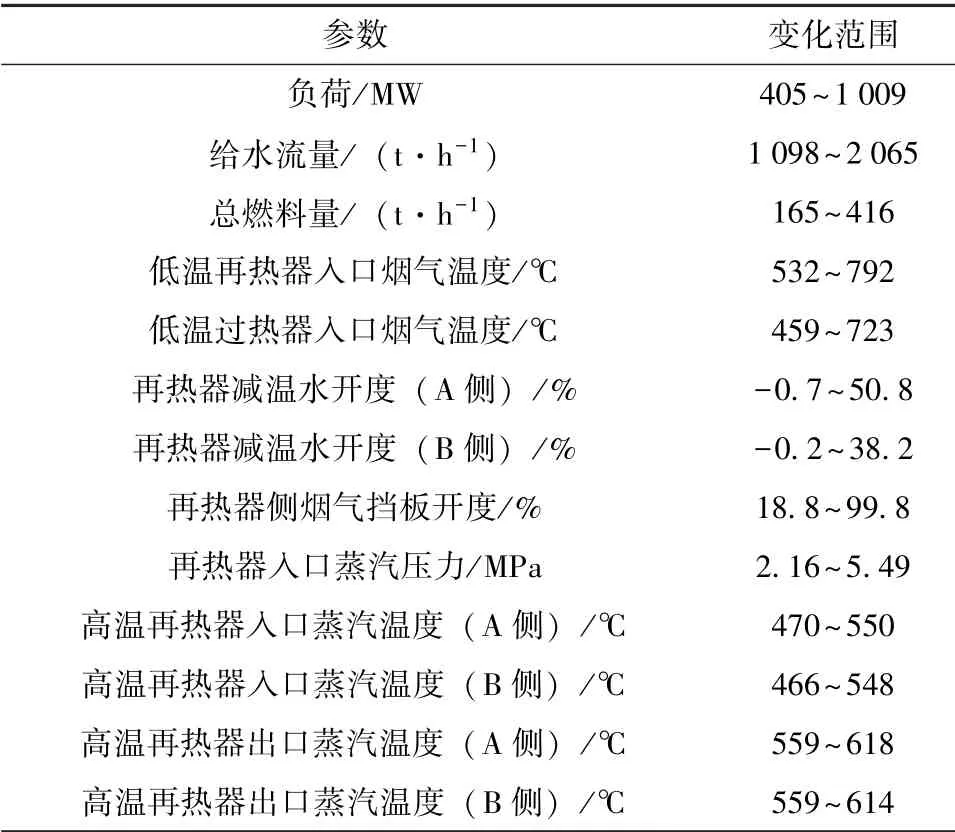
表1 各参数单位及变化范围

1.2 多层感知器神经网络

多层感知器神经网络(MLP)的概念最先由Rosenblatt于1952提出[11]。多层感知器神经网络是人工神经网络的一种，一般由一个输入层、几个隐藏层和一个输出层组成。人工神经网络由一组输出连接构成[12]，每个连接都有对应的权重，所有输入经过加权之后与偏置相加，通过激活函数来转化输出，使得其幅度范围缩小到有限值[13]。其数学表达式为:

MLP神经网络的不同层之间是全连接的，如图1所示。在输入层有M个神经元，则第1个隐藏层的输出表达式为:

图1 多层感知器神经网络结构

这个输出又可以作为下一个隐藏层的输入，隐藏层中任何神经元的输出表达式为:

式中，Wm，k1表示输入层和隐藏层神经元之间的权重，M和Kh分别表示输入层和第h个隐藏层神经元的数量，N则表示隐藏层的个数。

输出层神经元是通过对最后一个隐藏层加权求和得到的，其表达式为:

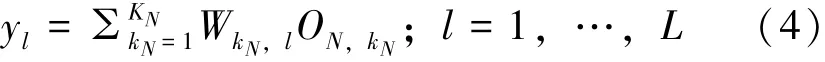
1.3 基于多层感知机的再热蒸汽温度预测建模

为了避免各输入参数由于数量级和变化范围不同所导致的建模效果不佳，对输入参数进行归一化处理。引入EarlyStopping[14]方法避免过拟合，该方法可根据指定的评价标准及时停止模型的训练。当连续n代训练模型的评价低于之前训练的最好结果时，立即停止模型的训练，这样就可以避免继续训练导致误差继续增大。激活函数选用线性整流函数(relu)。采用Adam优化器对MLP神经网络模型进行训练。Adam是一种基于低阶矩自适应估计的一阶梯度随机目标函数优化算法，该方法易于实现，计算效率高，内存需求少，非常适合于数据或参数较大的问题，同时也适用于非平稳目标和非常嘈杂或稀疏梯度的问题。超参数有直观的解释，通常需要很少的调整。文献[15]将Adam的各参数设置为:学习率0.001；1阶矩估计的指数衰减率0.9；2阶矩估计的指数衰减率0.999；模糊因子10－8。

使用三个评价标准对模型进行评价，分别为均方误差(MSE)、平均相对误差(MRE)及相关系数(r)，其公式分别为:

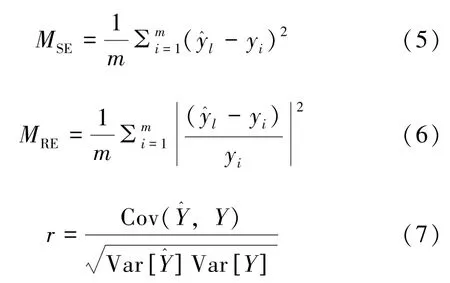
式中，y＾l、Y＾表示预测值，yi、Y表示实际值。

2 结果与分析

2.1 计算结果

采用基于多层感知机对再热蒸汽温度预测建模需对时间步长、网络层数、隐藏层节点数及训练批次数据量大小进行优化。时间步长优化如图2所示，计算时采用双层感知器，隐藏层节点数为32，将每次训练抓取的数据量(batch＿size)设置为256。由图可以看出，时间步长设置太小或太大都会导致MSE较大，当时间步长为2或3时，训练集和测试集的MSE较小。在保证模型精度的情况下，考虑计算所需时间和资源，最终选择时间步长为2，即取当前时刻及上一时刻数据作为模型输入。

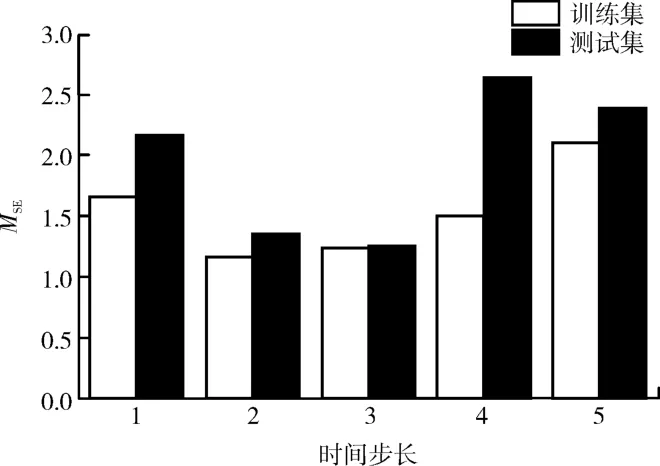
图2 时间步长调参结果

多层感知器的隐藏层调参结果如图3所示，其中时间步长为2，隐藏层节点数为32，将每次训练抓取的数据量(batch＿size)设置为256。由图可以看出，单层感知器即可满足精度要求，随着层数的增加，MSE逐渐增大，过拟合现象越来越严重。综合考虑，最终选用单层感知器。

图3 多层感知机层数调参结果

多层感知器的隐藏层节点数调参结果如图4所示，其中时间步长为2，隐藏层数为1，将每次训练抓取的数据量(batch＿size)设置为256。由图可以看出，隐藏层节点数较小时精度较高，随着节点数的增加，MSE逐渐增大，过拟合现象也是越来越严重。综合考虑，最终选用隐藏层节点数为32。

图4 隐藏层节点数调参结果

多层感知器的每次训练抓取的数据量(batch＿size)调参结果如图5所示，其中时间步长为2，隐藏层数为1，隐藏层节点数为32。由图可以看出，抓取的数据量大于32时训练集和测试集的MSE都相差不大。随着抓取的数据量的增多，每一代的训练时间越少，而代与代之间的收敛越慢。综合考虑，最终选用抓取的数据量为64。

图5 抓取的数据量调参结果

经过对模型参数的调整，最终选用单层感知器，时间步长为2，隐藏层数为1，隐藏层节点数为32，激活函数选用线性整流函数(relu)，每次训练抓取的数据量(batch＿size)为64。其训练过程如图6所示，可以看出，在第30—35代的评价指标已不下降，并在35代时停止了训练，用时约35s，因此MLP的训练过程收敛很快。

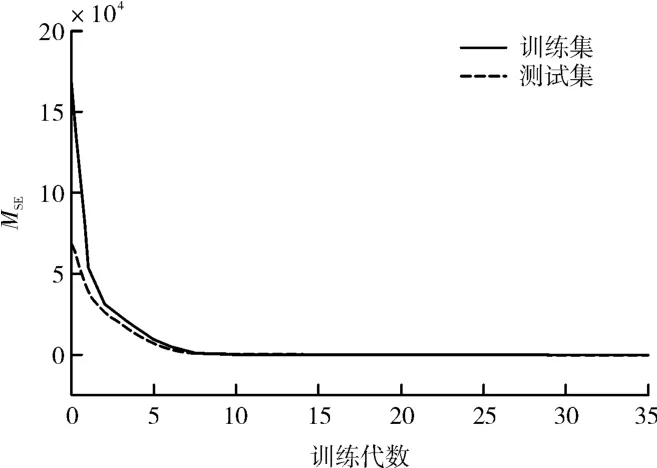
图6 MLP训练过程

由于数据量过大，无法完全显示于图上，故随机选取了部分训练集和测试集的预测值与实际值，以差值作为误差，如图7所示。可以看出，总体上预测值与实际值基本重合，在再热蒸汽温度较低时也能很好地进行预测，绝对误差在0附近波动，波动范围不大，说明MLP所训练出来的模型有很好的预测能力。

图7 再热蒸汽温度预测效果

图8 为训练集和测试集的预测值与实际值之间误差的频率分布图，可以很明显地看出不论是训练集还是测试集的误差都基本呈期望为0的正态分布。约有93.0%训练集和93.3%测试集样本的误差绝对值位于－1.5～1.5℃之间，其中有49.1%训练集和49.2%测试集样本的误差绝对值位于－0.5～0.5℃。

图8 MLP模型训练误差与分布比例

2.2 再热蒸汽温度预测建模效果对比

除MLP外，还采用LSTM和SVM对再热蒸汽温度进行了建模。表2显示了不同建模方法的预测效果，MLP训练模型的训练集和测试集的MSE、MRE及r的效果都较好，且训练集和测试集的预测效果相差不大，训练用时也较短；LSTM训练模型的MSE都小于0.8℃，MRE都为0.001%，r大于0.989，但综合训练效果均差于MLP，用时也较MLP长；SVM训练模型的训练集预测效果较好，其MSE低至0.309℃，但其测试集的MSE高至1.728℃，普适性很差，训练用时大于25 min，总体而言预测效果不佳。综上，MLP的预测效果要好于LSTM及SVM。

表2 不同建模方法的预测效果对比

3 结语

本文以某1 000 MW超超临界燃煤锅炉为研究对象，建立基于多层感知器神经网络的再热蒸汽温度预测模型。结果表明，MLP训练模型的均方误差小于0.71℃，平均相对误差小于0.001%，相关系数大于0.991，相较于LSTM和SVM模型，具有更好的预测精度，泛化效果且训练用时很短，能够很好地对再热蒸汽温度进行预测，将该模型预测结果引入控制器有助于提高再热蒸汽温度控制品质。