一类H-Toeplitz算子的复对称性
陈 泳,赖丽玲,梁金金
(1.浙江师范大学 数学与计算机科学学院,浙江 金华 321004;2.杭州师范大学 数学学院,杭州 311121)
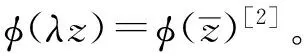
1 预备知识
1.1 研究背景



(1)

Tφ=PMφ,Hφ=PMφJ,
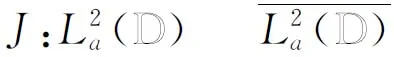


Bφ=PMφK。
由定义可以看出,H-Toeplitz算子与Toeplitz算子和Hankel算子紧密联系。事实上,对于每个非负整数n,有
Bφ(e2n)=PMφK(e2n)=PMφ(en)=Tφ(en);
(2)
Bφ(e2n+1)=PMφK(e2n+1)=PMφJ(en)=Hφ(en)。
(3)


2)C2=I,即C是对合。

令α=(α0,α1,α2…),其中每个|αn|=1,n=0,1,2…。定义复共轭Cα为
Cαen=αnen,n=0,1,2…。



(4)
其中每个φk为径向函数,
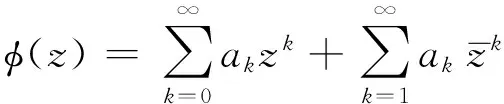
1.2 引 理
引理1对于非负整数s和t,有以下公式成立:
对于调和符号的H-Toeplitz算子,有以下结论。

和
证明:首先有
由引理1,当m≥n时有
而当m 对于Hankel算子,类似有 由此及前面的证明,结合式(2)~(3)即知引理2的结论成立。 为了证明定理2,需要下面关于拟齐次符号H-Toeplitz算子的结论。 引理3令p为整数,n为非负整数,φ为有界径向函数,则以下结论成立: 当n+p<0时,由上述计算过程可知Beip θφ(z2n)=0。同理,当n+1≤p时, 当n+1>p时,由上述计算过程可知Beip θφ(z2n+1)=0。综上即知结论成立。 本研究首先考虑调和函数符号的H-Toeplitz算子关于复共轭Cα的复对称性。 (5) 当2m+1 (6) 令k=2m+1-n≥0,则2m=k+n-1代入式(5)可得: (7) 令j=n-2m-1≥1,则n=j+2m+1代入式(6)可得: (8) 注意到 因此在式(7)和式(8)中分别令n→∞,m→∞,可得: ak=0,k≥0;bj=0,j≥1。 对于符号为式(4)所示的H-Toeplitz算子,尚不清楚上述结果是否成立,但在某些限制条件下,上述结论仍然成立。 则当2m+1≤n+N时,有 同理由引理3可知,当n≥max{N,0}时,有 因此当2m+1≤n+N且n≥max{N,0}时,有 令k=2m+1-n,则对于每个k≤N,由上述计算得到: 本研究探讨了Bergman空间上一类H-Toeplitz算子关于给定复共轭Cα的复对称性。从特殊符号入手,通过考察调和函数符号或非调和函数符号的H-Toeplitz算子,来研究该算子关于Cα的复对称性。结果表明,当符号为调和函数符号或由拟齐次函数的和组成的非调和函数符号时,对应的H-Toeplitz算子关于给定的复共轭为复对称当且仅当该符号为零。

2 主要结果

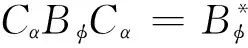


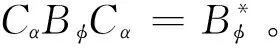

3 结 语

