基于3D heatmap 的人体三维姿态估计方法

严 曲， 李 由*， 甘叔玮

(1.中国航天员科研训练中心人因工程重点实验室， 北京 100094； 2.中山大学航空航天学院， 广州 510275)

1 引言

航天员在轨长期驻留期间，除了开展航天器的日常管理外，还要完成在轨组装、维修以及各类复杂的科学实验。 因此，监测并分析其工作负荷，合理安排在轨任务，对于保障航天员身心健康以及任务成功实施具有重要意义。

对航天员执行任务期间的姿态进行测量可以获取其长期在轨的运动特性，分析其任务期间的操作特点、工作负荷，从而为合理进行任务规划提供依据。 人体运动捕捉可分为接触式和非接触式2 类方法。 接触式方法通过在人体关键部位(肢体、躯干)安装惯性传感器，实时采集佩戴部位的加速度、角速度等信息，实现姿态还原。 非接触式方法主要采用光学传感器，如红外相机、彩色相机、深度相机等，一般采用多目配置，从各个角度获取人体运动图像并从中解算人体关节的位置和角度。 这种基于光学的方法又可分为2 类:①有标记光学运动捕捉，如Vicon、OptiTrack、Qualisys 等系统，通过对人体表面放置的光学标记球进行高精度定位，实现人体运动捕捉；②无标记光学运动捕捉，主要基于计算机视觉人体姿态估计算法，精度稍低，但是系统布设简单。 随着计算机视觉的不断发展，无标记光学运动捕捉精度不断得到提高，便捷性的优势逐渐凸显。 受在轨航天器空间狭小、上行资源受限、便捷性要求高等条件制约，无标记光学人体运动捕捉系统是实现航天员运动数据捕获的最佳途径。

为了应对复杂场景下肢体的遮挡和自遮挡，可以通过增加不同视角的视图来弥补单视图信息的缺失。 近年来从多视图序列图像估计精确的三维人体姿态取得了重大突破。

多视图的三维人体姿态估计分为2 种。 第一种是判别类方法，基本思想是将复杂人体简化为模型(例如棍棒模型、圆柱体模型、SMPL 模型等)，然后通过迭代优化模型参数，使得模型特征在各个视图中投影与从图像中提取出的特征逐步匹配优化，其本质为参数估计的最大似然概率问题。 Gall 等针对模型参数的优化问题提出了一个多层次框架，融合随机优化、滤波算法以及局部优化，提高了参数估计精度；Liu 等提出了一种结合图像分割和目标跟踪的算法，采用人体形貌模型与图像中的对应人体像素进行匹配优化，实现了多人交互下的人体运动跟踪；赵勇等提出了一种条件先验人体模型，根据图像内容自适应调节关节间在二维图像上的先验分布，对关节定位进行约束。 第二类是生成类方法，该方法不依赖人体模型，直接从二维图像中获得人体关节点的图像坐标，并通过多视图几何重建得到三维人体姿态。 近年来，卷积神经网络的发展使得从图像上提取二维人体关键点的精度愈来愈高，例如OpenPose，AlphaPose，HR-Net等。 生成类方法通过多视图的优势，融合各个视图得到的人体关键点位置信息，是近年来三维人体姿态估计的研究热点。 其中，多视图融合主要有2 个热点问题:①多人姿态估计时，需要建立跨视图匹配关系。 Dong 等利用形貌相似性和几何约束建立多视图匹配矩阵，并采用凸优化的方法对跨视图的匹配矩阵进行优化，获得准确的多人在跨视图间的关系。 ②在存在遮挡情况下，当个别视图存在错误二维关键点检测时，如何优化得到高精度三维人体姿态问题。 Qiu 等通过构建交叉视图融合的卷积神经网络，将其他视图的信息融合到当前视图，从而提高了遮挡情况下二维关键点检测的精度；Zhang 等提出了AdaFuse 方法，训练端到端的卷积神经网络，通过自适应多视图融合权重，对存在遮挡的视图中的二维关键点检测结果的贡献进行抑制。

本文针对遮挡情况下的多视图三维人体姿态估计问题，利用当前二维关键点检测精度高的优势，通过融合多视图的关键点检测结果得到三维空间的关键点概率分布图(3D heatmap)，并结合人体模型的先验信息，采用期望最大化(Expectation Maximization，EM)算法得到准确的三维人体姿态估计结果，通过公开数据集Human3.6M测试本文算法的关节点估计精度，对比不同相机数量下的算法鲁棒性。

2 基于3D heatmap 的三维人体姿态估计

本文算法框架如图1 所示。 首先从多视图数据提取进行关键点检测，得到图像中的关键点位置分布(2D heatmap)，进而通过相机标定结果构建关键点在三维空间中的位置分布概率(3D heatmap)，最后结合人体先验模型，通过EM 算法迭代获得人体三维姿态数据。

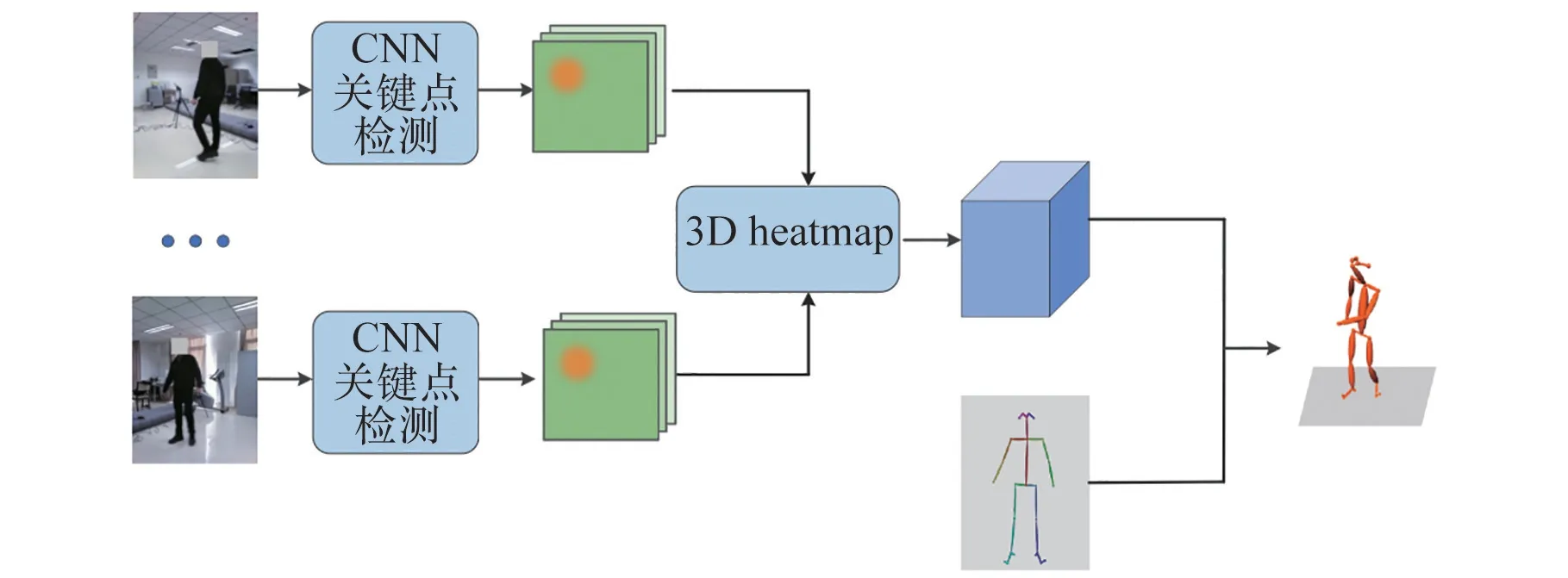
图1 算法框架示意图Fig.1 Schematic diagram of the algorithm

2.1 3D heatmap

2.1.1 2D heatmap 的获取

随着深度学习的发展，基于卷积神经网络(Convolutional Neural Networks，CNN)的人体二维关键点算法精度逐渐提升。 OpenPose 是当前使用最广泛的开源人体姿态估计框架，支持包括人体、面部、手势在内的二维关键点检测，可以准确描述复杂人体的运动。

OpenPose 采用自底向上的人体关键点检测策略，通过对图像中所有人的部位进行检测，获得2D heatmap 以及描述人体关节连接关系的部位亲和场(Part Affinity Field，PAF)，通过后处理将同一人的不同部位关联起来，实现多人的二维人体姿态估计。 相较于自顶向下的二维人体姿态估计，自底向上的OpenPose 不需要先检测人体框，对于图像中存在多人的情况，运算效率更高，可实时进行多人姿态估计。

2.1.2 体素构建及3D heatmap 的构建

2D heatmap 描述了关键点在二维图像上的分布概率，通过提取其最大值可获得关键点图像坐标，在已知各相机参数的情况下，通过空间点交会即可获得三维人体姿态。 然而，由于2D heatmap只是关键点位置的概率性描述，所获得的关键点坐标存在误差，导致后续的空间点交会得到的三维人体姿态往往存在较大偏差。

因此，如何在三维空间中保留二维关键点检测的概率分布信息是获得高精度三维人体姿态的关键。 本文采用体素的方式构建3D heatmap，体素是对三维空间的离散化，通过××大小的体素{V} 描述人体所在的空间，其中，，为体素坐标系下的点。 体素中心位于人体盆骨所在位置，该位置由多视图下的二维盆骨关节点坐标交会得到。 体素方法的精度与分辨率存在精度与运算量的矛盾关系，本文体素坐标建立在人体盆骨附近2 m×2 m×2 m 的空间范围，分辨率采用128×128×128，每个体素的实际物理空间大小约为1.56 cm×1.56 cm×1.56 cm，运算量适中且精度满足需求。 体素中的元素描述了三维的人体关节点概率分布，记体素坐标系下的点(，，)与世界坐标系之间的转换关系如式(1)所示:

如图2 所示，对于每一个体素{V} ，将其转换至世界坐标系后，根据相机的外参数，投影至像面，并提取对应位置的2D heatmap 值(，)，＝1，2，…，，对各视图得到的2D heatmap进行融合，得到该体素的3D heatmap，如式(2)所示:

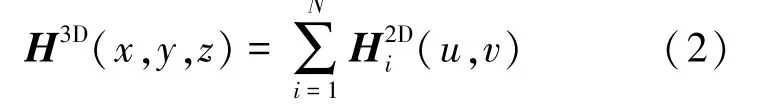
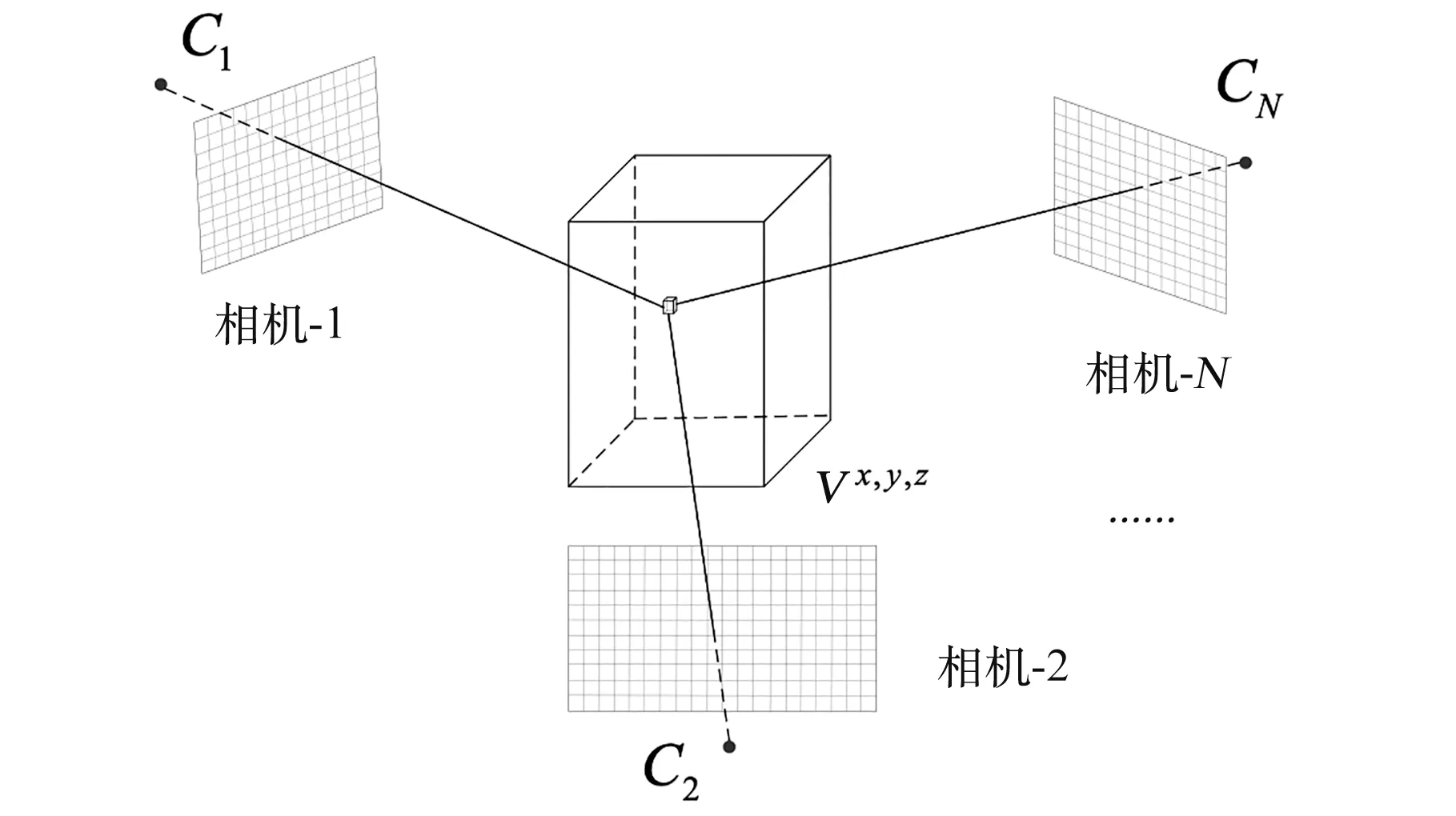
图2 构建3D heatmap 示意图Fig.2 Construction of 3D heatmap

2.2 期望最大化算法优化三维人体姿态

理论上，可以直接从3D heatmap 获取人体姿态，但是结果容易受到错误二维关节点heatmap的影响，这是因为OpenPose 获取的2D heatmap存在误差。 另一方面，3D heatmap 的特性是在该视图光轴方向上梯度较小，也就是关节在该方向上变化对关节点在3D heatmap 上的取值变化不大。 为克服上述不利因素，本文施加人体模型先验约束，通过模型本质蕴含的骨骼长度信息，利用EM 算法对关节点三维坐标进行优化。

2.2.1 三维人体姿态估计的概率模型

给定人体模型的参数，人体的三维姿态(关节点位置)，可通过式(3)分布概率进行建模:

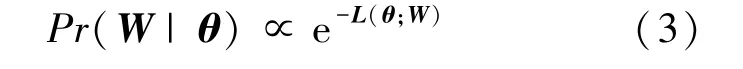
式中，＝{，，} 为人体参数作用下的人体姿态变形以及人体整体的旋转矩阵、平移向量的集合，损失函数(；) 定义如式(4)所示:

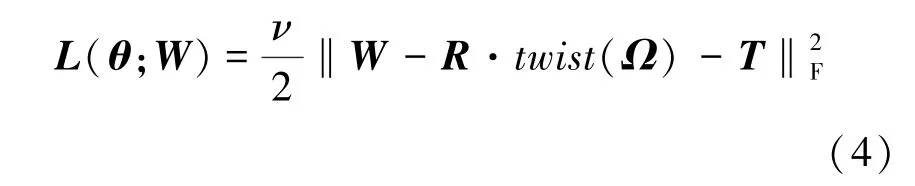
‖·‖为Frobenius 范数，(·) 为由人体姿态参数生成关节点坐标的映射函数，描述了由人体模型参数生成的三维人体姿态与实际的人体姿态之间的误差满足均值为的高斯分布。

在给定人体姿态的情况下，假设人体模型参数与该姿态下获得的3D heatmap 满足条件独立分布。 因此，的似然函数如式(5)所示:

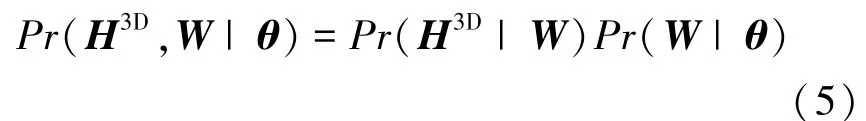
式中，似然函数() 描述了给定三维人体姿态后的3D heatmap 概率分布，本文通过式(2)构建的3D heatmap 获得该概率分布，如式(6)所示:

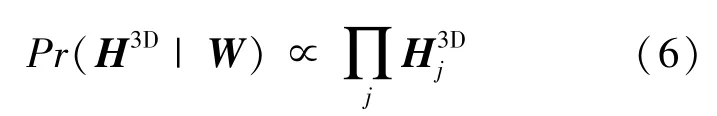
式中， 为关节的3D heatmap。

2.2.2 期望最大化算法

理论上，通过求解( ｜θ) 的最大似然估计问题，即可获得当前3D heatmap 下最符合的人体姿态。 然而，由于参数维度较高，无法直接求解，因此，本文采用期望最大化算法EM 求解该最大似然估计问题。 EM 算法分别对概率分布(｜′) 和模型参数进行最大化。 EM 算法是一种迭代算法，迭代分为两部分，其中E 步通过固定前一次迭代的′求解，得到当前状态下三维人体姿态的期望[｜，′] ；M 步通过最大化E 步获得的求解得到。 EM 算法在初始化模型参数后开始迭代，迭代中E 步和M 步交替进行。

E 步通过计算对数似然函数的期望来更新给定数据(3D heatmap)和前一步迭代的三维人体模型参数′的情况下三维人体姿态的条件分布概率，如式(7)所示:

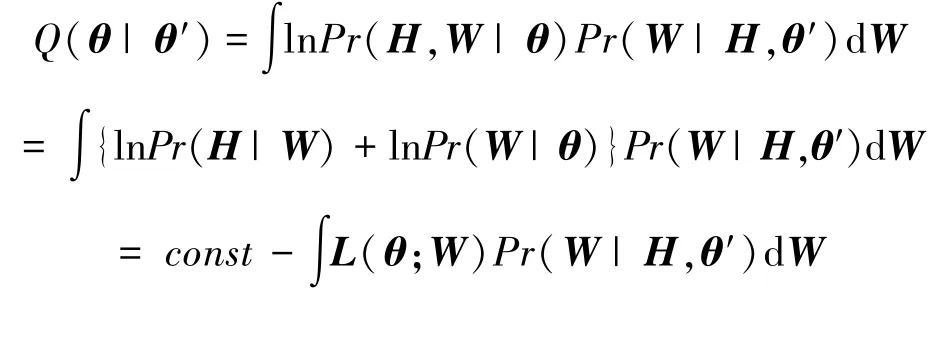
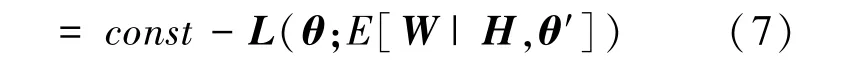
式中，为常数项，[｜，′] 为给定3D heatmap 和前一步迭代估计的人体模型参数′的情况下三维人体姿态的期望，其表达式如式(8)所示:

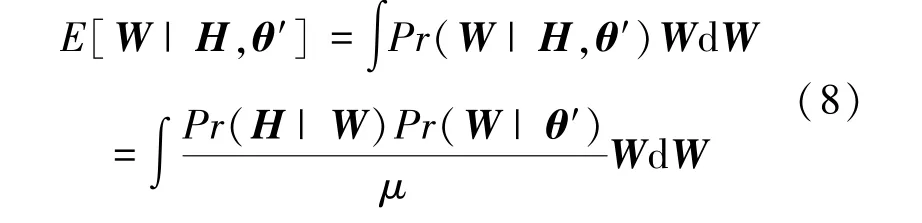
式中，为概率归一化系数。 M 步通过E 步获得的三维人体姿态的条件分布概率来最大化似然概率，得到当前最优的人体模型参数，如式(9)所示:

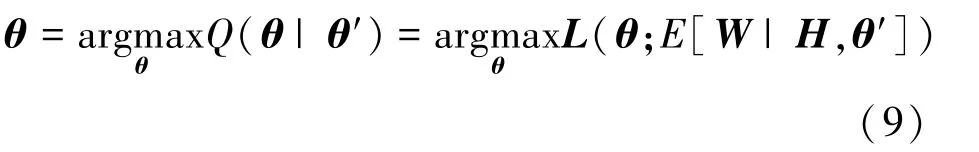
2.2.3 人体模型参数的优化

人体姿态变形通过关节转动角度与人体初始模型(T-Pose)进行表征，通过3D 扫描，可获得包含其骨架长度信息的T-Pose 人体模型。 因此，通过各个关节的角度即可描述人体的运动过程，且在运动过程中，人体的各个关节点之间始终满足人体模型的骨架长度约束。

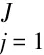
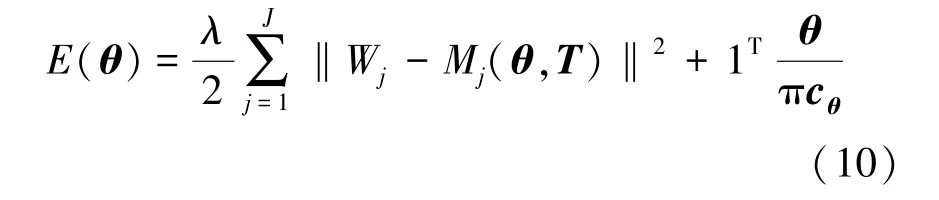
式中，为权重系数，M(，)为第个关节的人体关节位置， c为与同样长度的固定向量，描述了各关节的运动约束限制。 本文采用Levenberg-Mardqurdt 算法对该非线性优化问题进行求解，得到与当前关节点位置最匹配的模型参数。

3 实验分析

为了验证算法的有效性，在Human3.6M 数据集上进行算法验证。 Human3.6M 由360 万张人体活动数据图像组成，共有11 名实验者，17 个动作场景，采集数据由4 台分辨率为1002×1000的相机捕获。 图3 为4 个视图下的同一时刻的原始图像数据。

图3 Human3.6M 数据集4 个视图下原始图像Fig.3 Images of 4 camera views from Human3.6M dataset

通过OpenPose 检测获得2D heatmap，图4 为4 个视图下检测的2D heatmap 与原始图像叠加后的效果图。 本文采用OpenPose 的Body25 关键点检测配置，其关键点定义如图5 所示，共包含人体25 个关节点。 通过最大化期望算法迭代5 次后，得到的三维人体姿态如图6 所示。

图4 Human3.6M 数据集4 个视图下的人体2D Heatmap 估计结果Fig.4 Examples of 2D Heatmap estimated from Human3.6M dataset

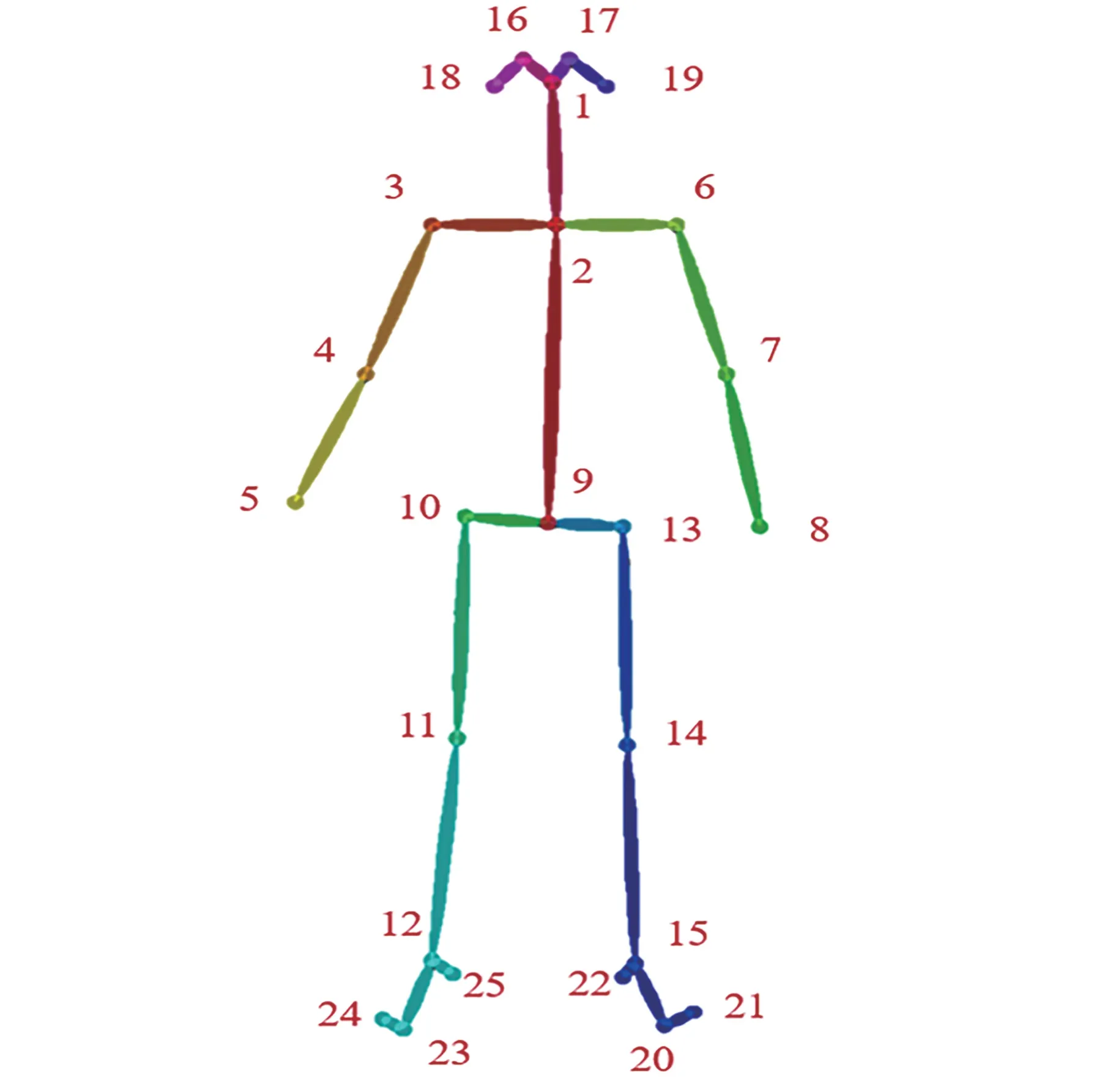
图5 OpenPose Body25 模型关键点定义Fig.5 Definition of OpenPose Body25 keypoints

图6 人体姿态估计结果Fig.6 Results of human pose estimation

为验证算法的有效性， 本文与基于RANSAC的多视图人体姿态估计以及代数三角化算法进行了对比。 算法精度评价标准采用平均关节点位置误差(Mean Per Joint Position Error，MPJPE)，即预测关键点和真值之间的平均欧式距离。 选择Human3.6M 数据集中的5 个动作集Dir.，Disc.，Eat，Sit 和Walk，对3 种算法进行了测试，算法精度对比结果见表1。 由表1 可知，在处理由于遮挡造成的关节点位置信息缺失时，本算法具有更好的稳定性。 尤其是由于Sit 数据集中存在大量的人体部位间遮挡和物体遮挡，二维关键点检测出现较多偏差，对后续的三维重建带来影响。 本文所采用的算法由于采用了人体模型作为约束，数据缺失带来的影响被降低，误差更小。

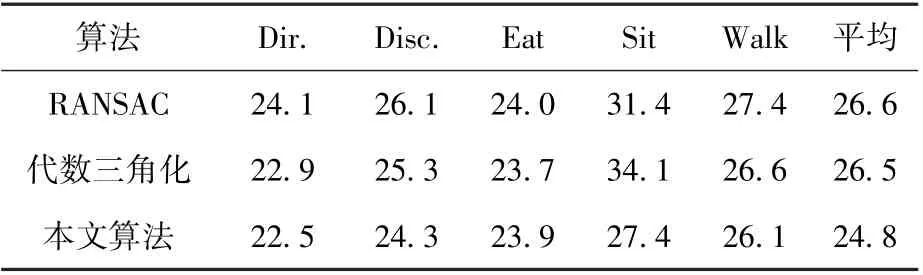
表1 Human3.6M 数据集算法精度对比结果Table 1 Comparison of algorithm precision for Human3.6M dataset mm

为验证不同相机个数对实验结果的影响，本文对相机个数从2 ～4 变化时的人体姿态估计精度进行了分析，处理结果见表2，可以看出，本文算法精度相较于RANSAC 方法和代数三角化方法更高，且受相机个数影响更小。

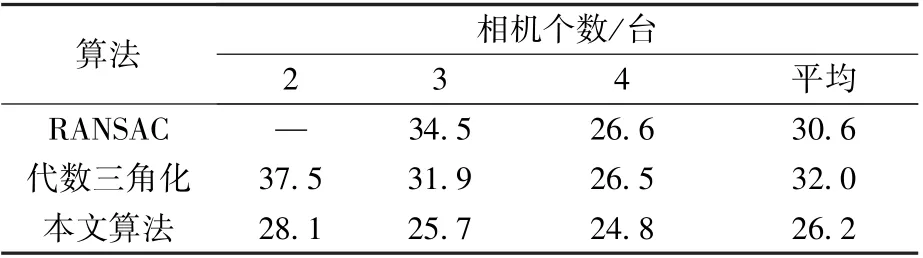
表2 相机数量分析Table 2 Analysis of camera numbers mm

4 结论

1)为了有效利用二维关键点检测结果的信息，本文采用反投影的方式在空间构建3D heatmap，可以有效保留图像中关键点提取的位置信息、概率分布信息。

2)提出了一种结合人体先验模型的三维人体姿态估计算法，可以有效提高部分视图存在遮挡情况下的人体关节点估计精度，具有良好的鲁棒性和精确性。

3)通过公开数据集Human3.6M 验证了算法的有效性，并对不同相机数量进行测试，测试结果表明，本方法不依赖于大量视图数据提供冗余信息，可以有效降低对相机配置的要求，适用于空间狭小、遮挡严重、相机数量有限的在轨航天员姿态估计应用场景。