SLIM 算法的9 轮不可能差分分析

郑会超 魏锦鹏

北京电子科技学院,北京市 100070

引言

分组密码是最成熟的密码分支之一,具有速度快、易于标准化和便于软硬件实现等特点,是一种非常重要的加密方案。 分组密码作为信息与网络安全中实现数据加密、消息鉴别及密钥管理的核心密码算法,在计算机通信和信息系统安全领域有着广泛的应用。 近年来,随着物联网的发展,无线传感器网络(WSN)和无线射频技术(RFID)的应用越来越广泛,它们具有硬件制造、维护成本低,网络健壮性、自组织性强,适用性广泛的特点,已成为物联网应用的关键组成部分。WSN 和RFID 基于无线网络传输信息,攻击者更加容易获得、干扰甚至破坏信息传输。 由于物联网上使用的微型计算设备计算能力有限,人们开始越来越关注轻量级分组密码算法的研究来保证信息的安全[1]。 轻量级分组密码算法作为一种特殊的分组密码算法,它们在硬件实现、加密速度、运行功耗等方面与AES 等传统分密码相比有明显的优势,更适合物联网微型计算设备使用。 在这种情况下,大量轻量级分组密码算法被研究出来,其中比较典型的有Lblock[2],LED[3],PRESENT[4], SIMON[5], Midori[6], SKINNY[7],HIGHT[8],SIMECK[9]等。

一个密码算法能够被广泛应用不仅应具有较高的实现效率,更重要的是保证算法的安全性。 然而,密码设计者在设计密码算法过程中,有时会追求高效性导致安全性降低,因此,采用多种密码分析方法去分析算法的安全性是很有必要的。 目前轻量级分组密码分析方法主要包括线性分析[10]、差分分析[11]、 截断差 分分析[12]、不可能差分分析[13]、积分分析[14]、相关密钥分析[15]、Biclique 分析[16]等。

2020 年,Aboushosha 等人提出了一个新的轻量级分组密码SLIM[17]。 Aboushosha 等人表明,SLIM 算法能有效抵抗差分分析和线性分析,并给出了7 轮差分路径和11 轮线性路径。 目前还没有文献对SLIM 算法进行不可能差分分析,本文试图对SLIM 算法进行不可能差分分析,以进一步评估其安全性。 本文充分利用了SLIM算法轮函数的具体细节,特别是挖掘非线性组件S 盒的差分性质,并结合P 置换设计,利用差分方程求解的方法构造出SLIM 算法的6 轮不可能差分区分器。 进一步,本文利用构造的区分器攻击了9 轮SLIM 算法,攻击的数据复杂度为229个选择明文,时间复杂度为255.83次9 轮加密。

1 SLIM 算法简介

1.1 SLIM 算法的整体框架

SLIM 算法整体采用Feistel 结构,轮函数采用类似于PRESENT 算法的SP 结构,其中S 盒为4 比特,P 置换采用16 比特的比特拉线设计。SLIM 算法的分组长度为32 比特,密钥长度为80比特,算法总轮数为32 轮。 该算法的整体加密流程如图1 所示。

图1 SLIM 算法的加密流程

在加密时,将32 比特的分组数据分为左右各16 比特,即左支Li和右支Ri均为16 比特。若一轮迭代的输入为(Li,Ri), 输出为(Li+1,Ri+1),则有:Li+1=Ri;Ri+1=Li⊕F(Ri,Ki),其中,Ki表示第i 轮的轮密钥,F 表示轮函数。

1.2 SLIM 算法的轮函数

SLIM 算法轮函数F 的加密流程由轮密钥加、S 层和P 置换3 部分组成,如图2 所示。

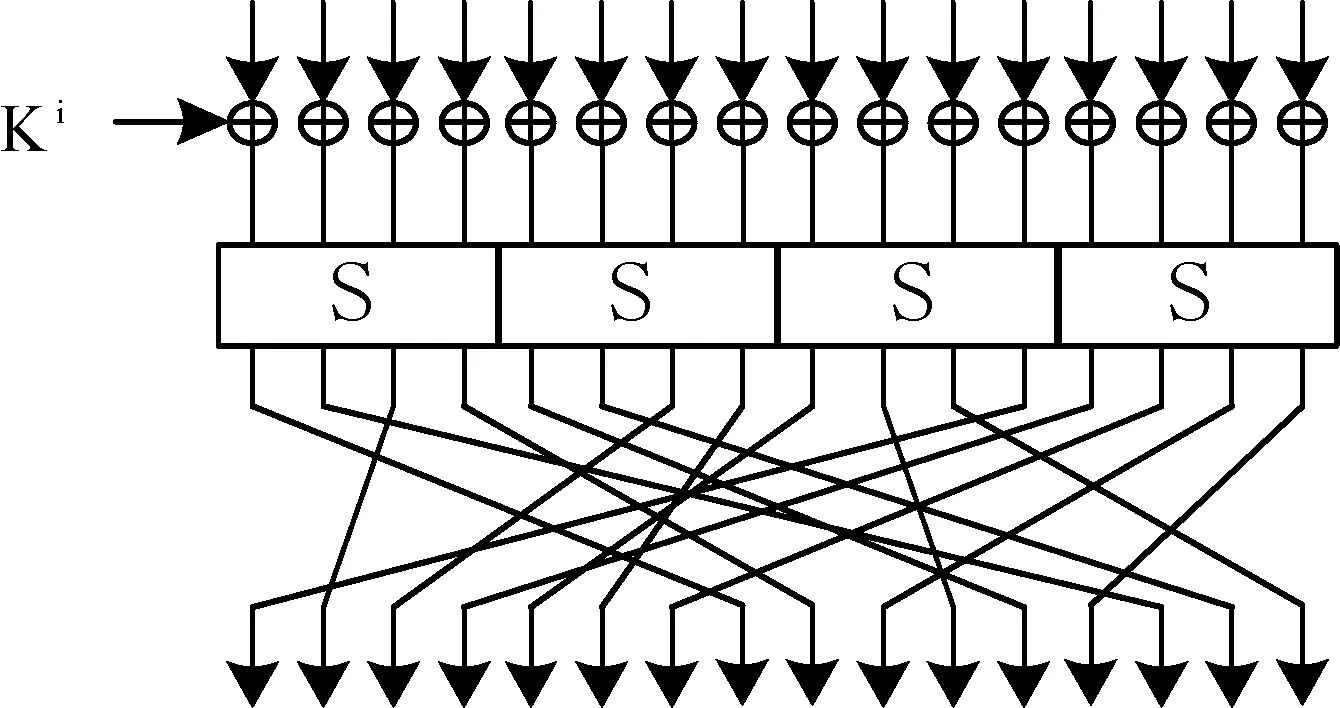
图2 SLIM 算法轮函数F 的加密流程

轮密钥加:分组加密数据的右支Ri与第i轮的轮密钥Ki进行逐比特异或。

S 层:由4 个相同的4 比特S 盒并行加密,SLIM 算法中的 4 比特 S 盒与国际标准PRESENT 算法的S 盒相同,如表1 所列。

表1 SLIM 算法的S 盒

P 置换:按照比特拉线设计,即16 比特数据按照表2 的规律进行比特置换。 在表2 中,输入的第i 比特经过P 置换后变为第P(i)比特。

表2 SLIM 算法的P 置换

在研究不可能差分区分器的构造时,由于轮密钥不影响差分的传播,因此本文不详细介绍SLIM 的密钥扩展算法,具体细节见文献[17]。

2 SLIM 算法的6 轮不可能差分区分器

构造尽可能长的不可能差分区分器是不可能差分分析的核心。 本节首先挖掘SLIM 算法S盒的具体细节,给出一个关于S 盒的差分性质;然后利用该性质,结合P 置换的加密流程,构造出SLIM 算法的一条6 轮不可能差分区分器。根据表1 给出的SLIM 算法的S 盒,利用python编程搜索S 盒的差分分布表,如表3 所示。

表3 SLIM 算法S 盒的差分分布表

在表3 中,第1 列为S 盒的输入差分,第1行为S 盒的输出差分,输入与输出差分均用16进制表示,中间的值为该输入输出差分方程对应的解的个数。 例如,当S 盒的输入差分为0x2时,输出差分为0x3 时,满足该差分方程的解的个数为2。 注意当解的个数为0 时,说明该输入差分和输出差分不匹配,即该输入差分经过S 盒后不能传播到该输出差分。

通过观察SLIM 算法S 盒的差分分布表,容易得到如下性质。

性质1 对于SLIM 算法的S 盒,当输入差分分别为0x1,0x8,0x9 时,经过S 盒后输出差分分别为***1,***1 和***0,以概率1 成立。其中*表示该比特差分可能为0 也可能为1。

证明 以0x8→***1 为例进行分析。 根据表3,当输入差分为0x8 时,输出差分可能为0x3,0x7,0x9,0xB,0xD,0xF,则输出差分前3 比特0 或1 均能够出现,但是最低比特差分一定为1,即输出差分的形式为***1。 因此,0x8→***1 以概率1 成立。 类似地,可以说明0x1→***1和0x9→***0 以概率1 成立。

下面利用性质1 并结合P 置换的特点,给出定理1。

定理1 在SLIM 算法中,当输入差分为(X,016),输出差分为(016,Y) 时, (X,016) →(016,Y) 是SLIM 算法的一条6 轮不可能差分区分器,如图3 所示。 其中X 满足(*12| 1000),Y 满足(012| 1000),*i表示连续i 个*,0i表示连续i 个0。 “｜”表示比特串之间的连接。

证明 首先从正向加密开始计算,正向输入差分为(X,016), 经过1 轮加密后输出差分为(016,X), 经过2 轮加密后输出差分为(X,F(X)),经过3 轮加密后输出差分的左分支为F(X),计算结果如表4 所示。

表4 输入差分X 的加密

然后从逆向进行运算,逆向的输出差分为(016,Y),由于SLIM 算法结构为Feistel 型,加解密运算是相同的,所以逆向解密运算的轮函数与正向加密的轮函数相同。 输出差分经过1 轮解密后,输出差分仍为(016,Y),经过2 轮解密后输出差分为(Y,F(Y)),经过3 轮解密后输出差分右分支为F2(Y) ⊕Y。 计算结果如表5 所示。

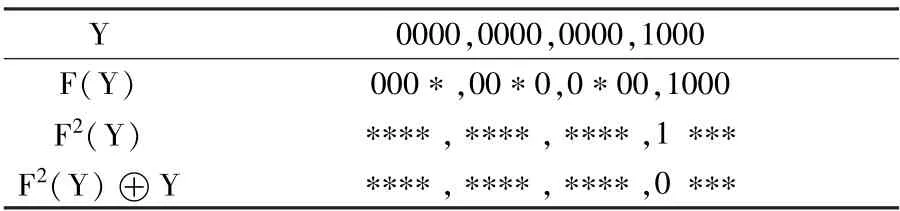
表5 输出差分Y 的解密

由图3 可知,需要对比正向加密3 轮的输出差分左分支与逆向解密3 轮的输出差分的右分支,即需要对比F(X) 与F2(Y) ⊕Y 的值,由表4 和表5 容易看出二者之间存在矛盾,故(X,016) →(016,Y) 是SLIM 算法的一条6 轮不可能差分区分器,定理1 成立。

图3 SLIM 算法6 轮不可能差分区分器

3 SLIM 算法的9 轮密钥恢复攻击

本节在上节构造的6 轮不可能差分区分器的基础上,添加1 轮前置路径和2 轮后置路径,对SLIM 算法进行9 轮不可能差分攻击。 图4 为攻击9 轮SLIM 算法的示意图。

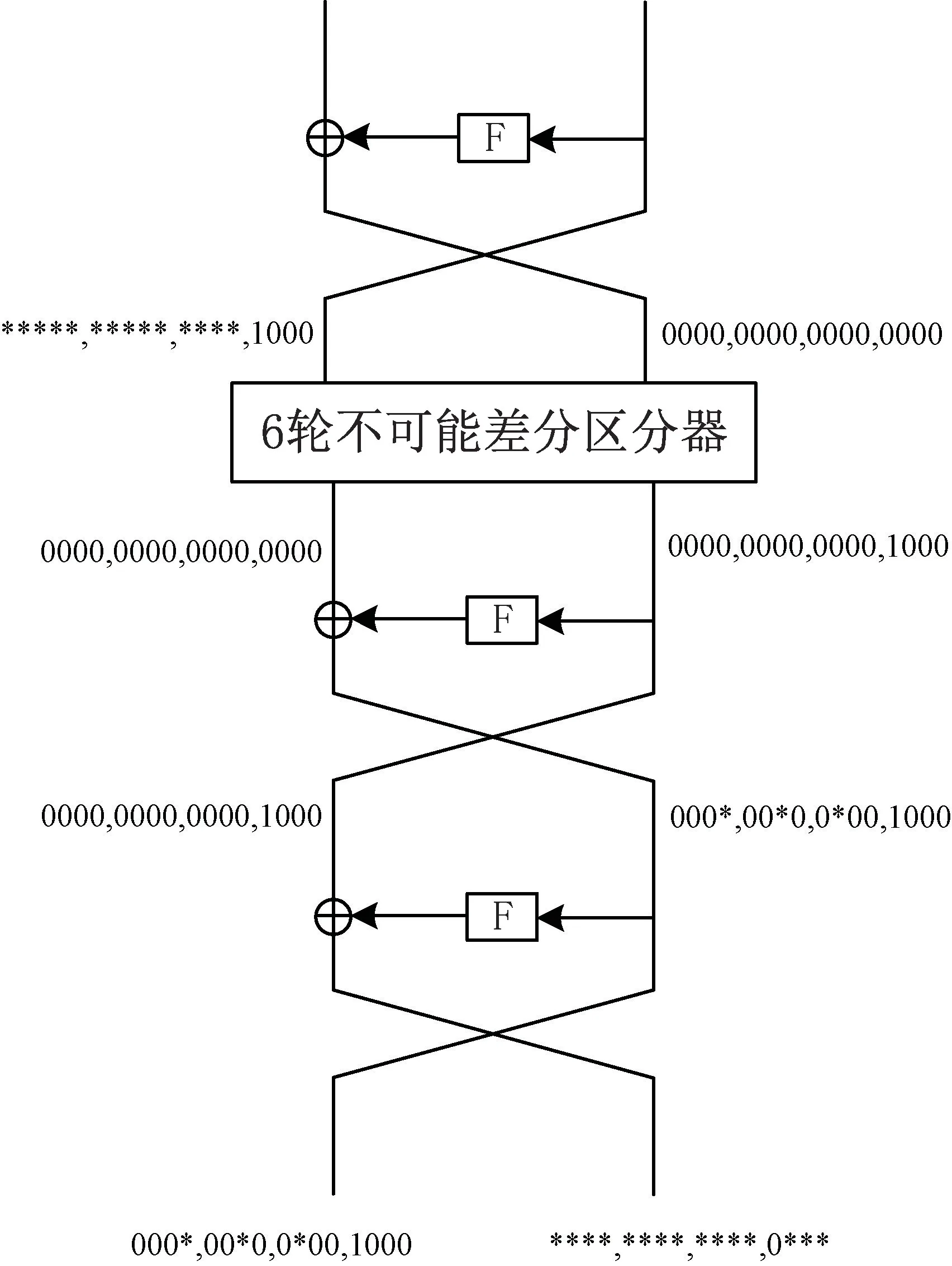
图4 SLIM 算法9 轮不可能差分攻击

步骤1 选取一个结构,在该结构内任意选择两个明文进行异或,它们的差分需要满足如下形 式: (****, ****, ****, 1***, ****,****,****,1000)。 该结构能够提供227个明文和253组明文对。

步骤2 选择2n个上述结构,则这些结构总共能提供2n+27个明文和2n+53组明文对。 选择密文差分满足以下形式的密文对留下:(000*,00*0,0*00,1000,****,****,****,0***),保留下来的明密文对数目约为2n+53× 2-14=2n+39。

步骤3 对于保留下来的明密文对,猜测最后一轮的轮密钥K9的全部16 比特密钥,即～,使得关于4 个S 盒的差分方程都成立。在平均意义下,每4 个比特通过S 盒使差分方程成立的概率约为2-4,则4 个差分方程同时成立的概率为2-4×4。 因此,经过步骤3 后剩余明密文对的数目约为2n+39× 2-16= 2n+23。

步骤4 对于剩余的明密文对,猜测第8 轮的轮密钥K8的低4 比特密钥,即～,使得关于最右边S 盒的差分方程成立,差分方程成立的概率约为2-4。 因此,经过步骤4 后剩余明密文对的数目约为2n+23× 2-4= 2n+19。

步骤5 对于经过上述步骤处理的剩余明密文对,猜测第1 轮的轮密钥K1的全部16 比特密钥,即～,若关于4 个S 盒的差分方程都成立,则筛除步骤3 到步骤5 中猜测的36 比特密钥。

当猜测的36 比特候选密钥满足不可能差分的输入输出时,猜测的密钥一定是错误的,密钥是错误的概率是2-16。 经过2n+19组明密文对的筛选,最终剩余错误密钥的个数N=(236- 1)×(1- 2-16)2n+19。 为使N≪1,本文取n=2,此时错误密钥都被淘汰,剩下的即为正确密钥。

复杂度分析:在上述攻击中,当n=2 时,数据复杂度为229个选择明文。 时间复杂度主要由步骤3 到步骤5 提供。 在步骤3 中,解密过程涉及4 个S 盒,而1 轮解密共涉及4 个S 盒,因此步骤3 的时间复杂度为2× 241× 216× 4/4=258次1 轮解密;在步骤4 中,解密过程只涉及1 个S 盒,因此步骤4 的时间复杂度为2× 225× 216×24× 1/4= 244次1 轮解密;在步骤5 中,加密过程涉及4 个S 盒,而1 轮加密共涉及4 个S 盒,因此步骤5 的时间复杂度为2× 221× 216× 24×216× 4/4= 258次1 轮加密。 故总的时间复杂度为258+ 244+ 258≈259次1 轮加密,即259÷ 9 ≈255.83次9 轮SLIM 算法加密。

4 结束语

本文主要研究了SLIM 算法在抵抗不可能差分攻击时的安全性问题。 通过仔细研究轮函数的结构,本文构造了SLIM 算法6 轮不可能差分区分器,并利用该区分器攻击了9 轮SLIM 算法。 通过上述攻击可以恢复K1的16 比特密钥,K8的4 比特密钥和K9的16 比特密钥,共计36比特密钥信息,该攻击的数据复杂度为229个选择明文,时间复杂度为255.83次9 轮加密。 本文研究表明SLIM 算法在抵抗不可能差分攻击时有足够的安全冗余。 SLIM 算法是否存在更长的不可能差分区分器是我们下一步的研究工作。