基于粗糙集的电池储能电站海量数据处理方法

陈娟，惠东，范茂松，胡娟，褚永金

(中国电力科学研究院有限公司, 北京 100085)

0 引言

储能技术具有很高的战略地位，世界各国一直都在不断支持储能技术的研究和应用[1-2]。2018年全球储能电站部署容量约为150 GW·h，预计2030年储能容量将增至380 GW·h[3]。同时，由于磷酸铁锂电池成本的下降，中国新建储能电站通常采用磷酸铁锂电池的方案。照此趋势发展，储能电站在线检测技术的应用市场需求会随着新储能电站的建设和旧储能电站的维护而逐年增大。

储能电站从运营的初始阶段至全寿命周期结束会产生海量的数据信息。电站的结构和特点决定了其数据量比光伏电站更加庞大，一个50 MW/100 MW·h的磷酸铁锂储能电站由十几万节电池单体组成，仅电池管理系统（battery management system, BMS）[4]一个月的数据量即可达 25 GB，一年的数据量可达300 GB，全生命周期的数据量可以达到3 TB。这样庞大的数据不仅会占用大量的磁盘和数据存储空间，对于在线数据处理和电站的机器自动评估更提出了巨大挑战。电站的在线评估数据挖掘工作需要有重点有层次地进行。对于储能电站的海量数据，在挖掘之前需要将数据分类成频繁精细处理的数据及对象和普通手段处理的数据及对象。处理挖掘的过程根据分类的结果有繁有简，这样在线处理算法和数据处理方法将被主要应用于选定的特定数据集，从而忽略另一些数据或者将其他数据只做基本逻辑和阈值的判断。

针对上述问题，本文提出利用粗糙集方法对数据属性进行约简，将单体电池划分为频繁检测对象和普通检测对象，从而压缩在线处理的数据量。在此基础上，选取某储能电站特定工况下一个电池簇的实测数据进行验证，证明方法的有效性。

1 储能电站数据特点分析

储能电站采集的数据中主要包括BMS数据、储能变流器（power conversion system, PCS）数据和调度策略等数据，其中占比最大的是BMS数据。以一个储能电池簇[5]的BMS数据为例，包括占据绝大多数的单体电压、温度信息，以及上百单体数据组成的簇电压、电流、温度、荷电状态（state of charge, SOC）SOC等信息。电池单体为储能电站在线评测的最小单元。单体电池的开路电压（open circuit voltage, OCV）VOC与电池的SOC具有一一对应关系。SOC是直接反应单体电池可用容量的物理量，但是在磷酸铁锂电池的主要充放电工作区间，SOC取值为10%～98%，VOC的变化只有160 mV，并且在线情况下难以准确获取，如图1SOC-VOC曲线所示。由于传感器和电路采集精度的问题，目前市面上主流的电压采集方案的精度为±2 mV[6]，这种精度难以满足磷酸铁锂电池在平坦区和识别区的荷电状态的分析[7]。差分电压分析[8-9]( differential voltage analysis，DVA)是一种广泛使用的用来提取电池特征的方法，即利用dV值可以反映电池电压相对电池容量的变化率[10-11]。dV值是反映电池状态的灵敏且实时性高的参数，DVA可以规避电池电压在线测量不准确的问题。单体温度值T是直接反应电池安全的参数，温度值包含电池充放电自身发热的信息，也包含结构散热设计和电池空间位置的信息。以上数据在线测量精度不够，另外，一簇电池的样本量高达几百个，它们在同一采集时刻所展现的同类数据是不一致的。

图1 磷酸铁锂电池SOC-VOC曲线Fig. 1 SOC-VOC curve of lithium-iron phosphate battery

针对储能电站数据量大，数据本身不精确、不一致的特点，在不增加硬件成本的前提下，为了实现在线评估的实时性和准确性，需要结合数据挖掘的数学方法对有效参数进行识别，对数据本身进行简化，对研究对象进行分类，这是在线评估技术研究的重点。粗糙集理论作为一种适用于不精确(imprecise)、不一致(inconsistent)、不完整(incomplete)等各种不完备信息的有效工具，其优点一方面是其数学基础成熟，不需要先验知识；另一方面是简单易用。由于粗糙集理论创建的目的和研究的出发点就是直接对数据进行分析和推理，从中发现隐含的知识，揭示潜在的规律，因此是一种天然的数据挖掘或者知识发现方法。它与基于概率论的数据挖掘方法、基于模糊理论的数据挖掘方法和基于证据理论的数据挖掘方法等处理不确定性问题理论的方法相比较，最显著的区别是它不需要提供问题所需处理的数据集合之外的任何先验知识，而且与处理其他不确定性问题的理论有很强的互补性。

2 粗糙集理论以及应用

粗糙集理论由波兰数学家Z.Pawlak 于1982年提出，通过结合逻辑学和哲学中对不精确、模糊的定义，针对知识和知识系统提出了知识约简、知识依赖、知识表达系统等概念，并在此基础上形成了较完整的理论体系—粗糙集理论。粗糙集理论[12]把知识看作关于论域的划分，是研究数据集合分类的理论。

2.1 知识系统定义

2.2 粗糙集定义

2.3 可约简关系

可约简关系是在保持知识系统分类能力不变的条件下，可删除的不相关或不重要的关系。R为等价关系集合，等价关系r∈R，若ind(R)=ind(R－r)，则称r为R中的不必要等价关系，即可约简关系。R中所有必要关系组成的集合称为核，记为core (R)[12]。关系属性约简的过程就是求知识系统核属性的过程。

利用粗糙集理论对数据进行分类，考虑对在线数据分类的重复稳定性做出定义，引入时域因素，集合样本X={x1,x2,··· ,xn}对于时刻t1的分类与时刻t2的分类计为

不同时刻的分类重复率记为η，则

2.4 知识表达系统

在粗糙集理论中，一个知识表达系统可表示为S=(U, R, V, f)，其中U为论域，R为属性集合，V为属性值集合，f为一个信息函数，其对象的每个属性赋予一个信息值。决策表是一类特殊而重要的知识表达系统。设S=(U, R, V, f)为一个知识表达系统，R=C∪D，C∩D= ∅，称C为条件属性集，D为决策属性集。具有条件属性集和决策属性集的知识系统称为决策表。

2.5 粗糙集应用

目前，粗糙集已经在信息领域、人工智能、管理科学、医学、化学、材料学和地理学等方面得到成功应用。储能电站的海量数据受到采样精度的影响，在工作状态下不同电池的测量值会有离散度。簇内几百节电池的样本量又可以利用统计学分布揭示电池数据规律，因此将粗糙集理论与统计分布学理论[13-14]相结合来分析电站的海量数据是非常适合的。

3 利用粗糙集理论进行数据处理

粗糙集的思想是在保持论域分类不变的前提下尽可能地减少属性[15]。与决策无关的属性在很大程度上会增加计算复杂度[16]。属性约简的方法主要有2种：（1）采用学习算法来评估所选择的属性子集[17]；（2）根据属性重要度或者信息增益等选择属性[18-20]。利用粗糙集理论对储能电站的海量数据做预处理，参见图2的流程，处理数据时按照属性的重要度已经对属性进行了约简。

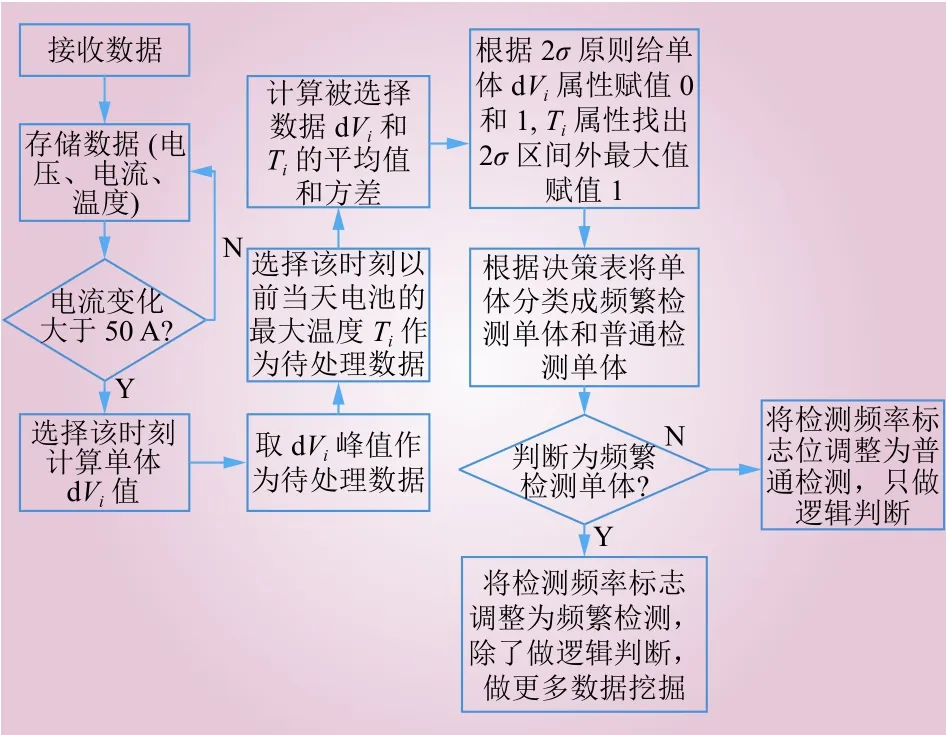
图2 数据处理流程Fig. 2 Flow chart of data processing

3.1 选择待处理的数据

本文选择受观察储能电站的一个箱体中任一电池簇2019年5月12日的工况下的BMS数据作为待处理数据，数据的更新频率为每分钟一次，电流值大于0为放电，小于0为充电，如图3所示。图3中红色标出的时刻电流变化率大于50 A/min，选择该时刻dV值作为待处理数据，电池静置1小时以后的单体数据作为VOC的取值。

图3 电池簇电流工况Fig. 3 Current working conditions of a battery cluster

3.2 确定研究对象和属性集合

一个电池簇中能够独立的最小单元就是电池单体，电池单体也是作为整个系统安全的最小单元，该电池簇由224节磷酸铁锂单体电池组成，所以论域U={x1, x2,··,x224}。

dV值在电池簇充放电过程中变化灵敏，将dV作为研究对象的属性之一；温度值在充放电过程中变化较慢，但是温度本身反映信息较多，包括空间位置信息、环境信息、电流积分信息等，因此将温度T也作为对象的研究属性之一。VOC是直接反映电池状态的参数。储能电站数据中停止充放电一段时间之后，才能获取VOC值，并且在线测量通常获取的只是VOC的一个点值，并非整条充放电曲线值。本文选择放电结束一段时间单体电压稳定的VOC值作为对象的研究属性。单体状态属性集合为C={dV，T，VOC}，设置属性C1=dV，C2=T，C3=VOC。

3.3 确定研究属性值

针对这224节磷酸铁锂单体样本，进行统计学分析，按照统计学2σ原则对数据进行二元逻辑划分，确定研究对象的属性值。首先分别绘制单体电压1分钟变化值dV、温度值T和OCV单体电压值VOC的分布直方图，分别如图4～6所示，其中dV、T和VOC均符合正态分布[21]，记作

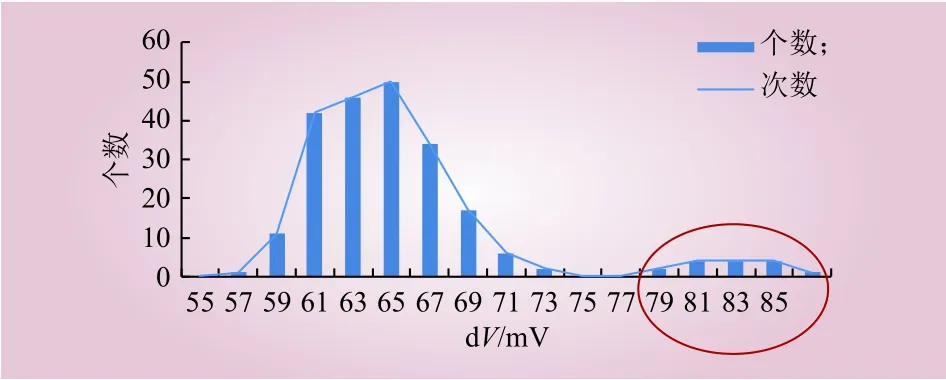
图4 dV分布Fig. 4 Statistical distribution of dV

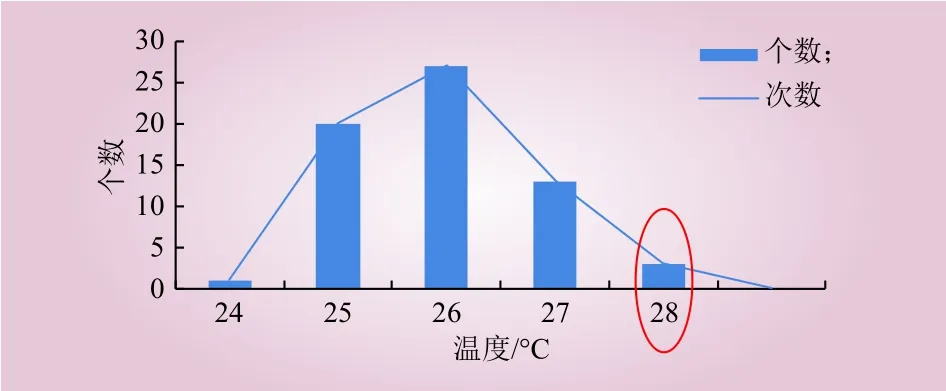
图5 温度分布Fig. 5 Statistical distribution of temperature

图6 VOC分布Fig. 6 Statistical distribution of VOC

3.3.1 单体电压变化值 dV

选取放电电流变化较大时刻传送的数据（图1中红色圈出时刻中的dV值）计算单体电压的dV的均值和方差为

在本文储能电池簇案例中根据式（8）（9）计算得到μdV=6 5 m V，σdV=5.5 m V， 视dV＞（μdV+2σdV）与 dV＜(μdV–2σdV)范围为小概率事件。统计分布直方图如图4所示，在本案例中，dV=79、81、83、85、87 mV 这些离散度较大的数据都属于重点观察单体数据，涉及单体15个，在分类过程中，将数据计为1（图4中被红色圈出的dV值）；在置信区间（54,76）以内的数据都记作0。

3.3.2 温度值

选择该电池簇64个温度采集点中温度最高的温度点对应的电池单体作为重点检测对象，分布直方图如图5所示。最高温度28℃对应3个温度传感器，每个温度传感器对应4节电池单体，共计12节单体电池，在逻辑分类中计作1（图5中被红色圈出的温度值），其余电池温度状态记为0。

3.3.3 电压值VOC

计算VOC的均值和方差为

根据式（10）（11）计算得到该时刻的电压均值为 µVOC=3.223V，σVOC=3 m V，视Voc＞ µVOC+2σVOC与V＜µVOC−2σVOC范围为小概率事件，统计分布直方图见图6。其中VOC=3.215、3.216、3.231 V的单体在OCV逻辑状态中被记作1（图中被红色圈出的电压值），其余2σVOC置信区间以内的OCV电压单体被记作0。

3.4 生成决策表

知识表达系统S=(U, R, V, f)，U为论域，R为属性集合，V为属性值的集合，f为等价关系。在储能电池簇的数据处理中，论域U为224节单体的 合U={x1,x2,···,x224}， 条件属性C={dV, T,VOC}包含3个属性，并且条件属性值都是二元逻辑值，所以由条件属性决定的状态集合最多有8种，论域U又可以划分为单体状态的集合U={X1, X2, X3, X4, X5, X6, X7, X8}；D为决策属性集合，D={是否作为系统频繁检测项}，决策集合D中0代表不作为系统频繁检测项，1代表作为系统频繁检测项；R为属性集合，R=C∪D；属性值V按照以上二元逻辑划分方法赋值。

结合200天的电站在线充放电数据，分别用dV、T和VOC值给电池单体人工分类，得到如表1的分类统计，表中的百分数是224个样本量的200天“最差”分类结果。由表1可以看出，dV和T的数据特点是绝大多数为“0”，少数为“1”，确定不了的可忽略不计；而VOC的数据特点是“0”和“1”的数据占比相差不多，而绝大多数属于确定不了的数据，也就是VOC判定为“0”时，决策属性的状态可以为“0”也可以为“1”，VOC判定为“1”时，决策属性的状态可以为“0”也可以为“1”，这使得VOC属性在影响决策属性的权重变得很小。

表1 200天数据分类Table 1 Data classification in 200 days

根据以上统计规律作属性值的二元逻辑划分，另外，根据5月份以前200天的电池簇的充放电数据人工分析的结果，生成决策表如表2所示。

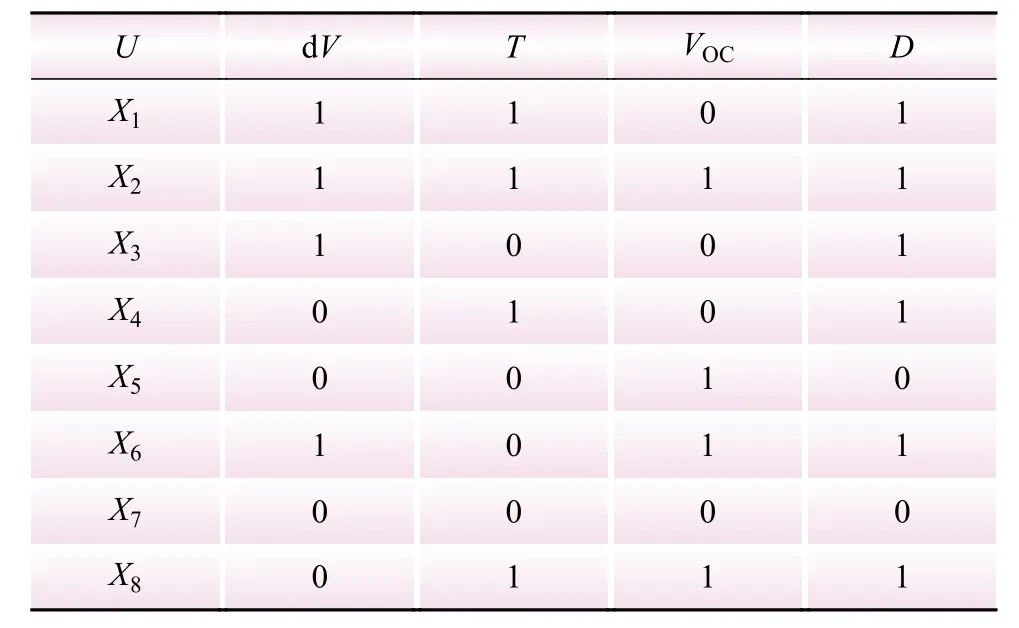
表2 生成决策Table 2 Decisions

通过粗糙集原理，对属性集进行约简，找到核属性，作为最终集合分类的属性，具体步骤如下。

（1）U按照dV属性分类得到，U/dV={{X1,X2,X3, X6},{X4,X5,X7,X8}}。

同时根据式(1)，POSdV(X)=U/dV，NEGdV(X)= ∅ 。

（2）U按照T属性分类得到，U/T= {{X1,X2,X4, X8},{X3, X5, X6, X7}}。

（3）U按照OCV属性分类得到，U/VOC={{X2,X5,X6,X8},{X1,X3, X4,X7}}。

（4）U按照dV和T属性分类得到，U/{dV,T}={{X1,X2},{X3,X6},{X4,X8},{X5,X7}}。

（5）U按照dV和VOC属性分类得到，U/{dV,VOC}={{X1,X3},{X2,X6},{X4,X7},{X5,X8}}。

（6）U按照T和VOC属性分类得到，U/{T,VOC}={{X1,X4},{X2,X8},{X3,X7},{X5,X6}}。

（7）U按照dV、T和VOC属性分类得到，U/C={{X1},{X2},{X3},{X4},{X5},{X6},{X7},{X8}}。

（8）U按照决策属性D分类得到，U/D={{X1,X2,X3,X4,X6,X8},{X5,X7}}。

（9）根据式(1)，按照dV、T和VOC属性和决策属性D分类得到，POSC(XD)={X1}∪{X2}∪{X3}∪{X4}∪{X5}∪{X6}∪{X7}∪{X8}。

（10）同理，按照T、VOC和决策属性D分类得到的正域，POS(C-dV)(XD) = {X1,X2,X4,X8} ≠POSCXD。

同理，按照dV、VOC和决策属性分类得到的正域，POS(C-T)(XD) = {X1,X2,X3,X6} ≠POSC(XD)。

同理，按照T、dV和决策属性D分类得到的正域， P OS(C−VOC)(XD)={X1,X2,X3,X4,X5,X6,X7,X8} =POSC(XD)。

综上所述，VOC是可约简属性，对决策来说是冗余项。因为在线检测的VOC数据由于传感器的精度限制，它的值在做统计分析过程中是不稳定的，这也是被约简的本质原因；而dV和T这两个属性只要符合电流变化较大的条件，程序设计中1min内的电流变化量在0.25C（0.25倍的电池容量）以上，就能够被在线系统检测出来，成为可以被识别的有用数据，并且展现出的规律是稳定的。在物理意义上验证了dV和T作为的核属性而VOC值作为非核属性的合理性。

不考虑dV和T属性作出的分类结果如下。

上述结果并不能等于由条件属性和决策属性综合分类的结果，所以，核属性为dV和T，核属性集合为core(dV+T)。

以表1为基准，约简后的决策表准确度为（1−不确定分类的单体百分比之和）×100%，即(1−1.3%−3.5%）×100%=95.2%。

3.5 数据应用和分析

应用核属性可以将224节电池单体中分离出需要频繁检测的电池编号为{cell8, cell 22, cell 36,cell57, cell58, cell59, cell60, cell64, cell78, cell85,cell86, cell87, cell88, cell89, cell90, cell91, cell92,cell106, cell120, cell134, cell148, cell162, cell176,cell190, cell 204, cell218}，见图7中5月12号分类图中所标示出的黄色色块，共计26个需要频繁检测的单体，占总样本量的11.6%。

图7 分类对比Fig. 7 Comparison of two detection classes

用同样的方法，处理2019年5月31日的数据，分离出的需要频繁检测的电池编号为{ cell8,cell22, cell36, cell57, cell58, cell59, cell60, cell64,cell78, cell85, cell86, cell87, cell88, cell89, cell90,cell91, cell92, cell106, cell120, cell134, cell148, cell162,cell176, cell190, cell 204, cell218}∪{cell50, cell53,cell54, cell55, cell56, cell105, cell107, cell108}， 见图7中5月31号分类图中所标示出的黄色色块，共计34个频繁检测单体，比5月12日的频繁检测项增加了8个cell，占总样本量的15.2%。

根据式（4），分类重复率为η=[(224−8)/224]×100%=96.4%。同样的方法处理2019年5月13—30日的数据，分类重复率都在90%以上。

4 结论

本文在对储能电站海量数据进行数据挖掘之前，利用粗糙集理论和统计学理论对数据进行预处理。研究表明，这一处理方法可以大大减少在线处理的数据总量，并且预处理后的数据具有很高的保真性。综合来看，本研究所给出的处理方法具有以下优点。

（1）属性约简后，待处理的数据保持与原数据基本相同的分类属性，使数据关系变得简洁，逻辑处理变得容易。

（2）将属性值利用统计学原理进行二元逻辑划分后，设备内存里的浮点属性值可以转化成逻辑值进行在线处理，大大减少了在线计算量。

（3）不同时刻的分类结果重复率高，结果稳定。对于分类集合中的频繁检测单体和普通检测单体，后续给它们赋予不同的数据处理周期，将进一步减小在线处理数据的压力。

综上，基于粗糙集的储能电站海量数据处理方法具有较好的适用性及应用价值，值得进一步开展深入研究。但是，由于在线采集数据的局限性，本文在数据分析过程中暂时没有引入更多的电池属性分析。因此，以粗糙集合理论为基本方法引入更多的属性进行数据挖掘工作将是下一步的重点研究方向。