适用于无直流侧电压传感器单相级联H桥型光伏逆变器的直接功率模型预测控制方法

张茜，毛义鹏，余乐,，杨皓

(1. 西南交通大学 电气工程学院，四川 成都 610031；2. 国网四川省电力公司，四川 成都 610000；3. 国家电网有限公司西南分部，四川 成都 610000)

0 引言

作为电能转换的枢纽，逆变器性能的好坏直接影响整个光伏系统的并网效率[1-3]。在众多逆变器拓扑中，级联 H 桥 (cascaded H-bridge ,CHB)型拓扑结构以其模块化程度高、输出波形频率特性好及布局简单等优点得到广泛采用[4-6]。

参考电机控制中直接转矩控制(direct torque control, DTC)方法，直接功率控制 (direct power control, DPC)方法分别针对瞬时有功功率及无功功率实现了有效控制[7-8]。文献[9]提出了一种新型DPC方法，该方法固定了系统开关频率。但是，该算法内环共有4个PI控制器，增加了系统的复杂度和PI参数整定难度。在此背景下，模型预测控制 (model predictive control, MPC)方法因其较高的控制精度，快速的动态响应以及无PI参数整定问题等优点受到了广泛关注[10-11]。其中，有限控制集模型预测 (finite-control-set MPC, FCS-MPC)方法将约束条件嵌入评价函数，并通过对评价函数滚动寻优，从而获得作用于变流器下一控制周期的最优开关序列[12-14]。但是，该算法存在着开关频率不固定以及计算量大等缺点。为了固定系统开关频率，文献[15-16]提出了基于虚拟磁链(virtual flux, VF)的 MPC-DPC 控制算法。

针对CHB型多电平逆变器而言，H桥数量的增加使得直流侧电容电压的平衡控制逐渐成为设计CHB型逆变器控制系统的一大难点。文献[17]给出了基于硬件电路的直流侧电容电压平衡方法。但是额外均压电路的引入增加了硬件成本，同时会限制多电平逆变器系统的扩展。针对以上问题，文献[18-19]提出了基于比例积分（PI）控制器的直流侧电容电压平衡算法。但是，相比于基于冗余开关状态的电容电压平衡控制方法，PI控制器的存在降低了系统的动态响应。

本文介绍了一种适用于无直流侧电压传感器单相级联H桥型光伏逆变器的直接功率模型预测控制方法，利用逆变器输出电压对直流侧电容电压进行估计，减少了系统传感器数量，降低了系统复杂度。采用串行计算的方式，在实现电容电压平衡控制的同时，提高了控制系统的扩展性。

1 光伏电池等效电路模型

光伏电池作为光伏阵列中实现光电转换的最小工作单元，考虑光伏电池自身具有低压、额定容量小的特性，需要采用串并联的方式组成光伏阵列。光伏阵列与光伏电池的工作特性与光伏电池相似，因此光伏电池的等效电路模型同样适用于光伏阵列。根据电子学理论，图1给出了光伏电池的等效电路模型。

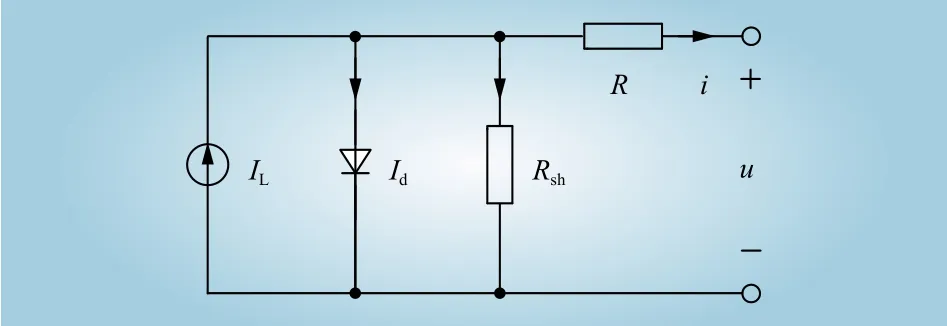
图1 光伏电池等效电路模型Fig. 1 Equivalent circuit model of photovoltaic battery

根据图1所示等效电路模型，给出光伏电池的i-u特性方程为

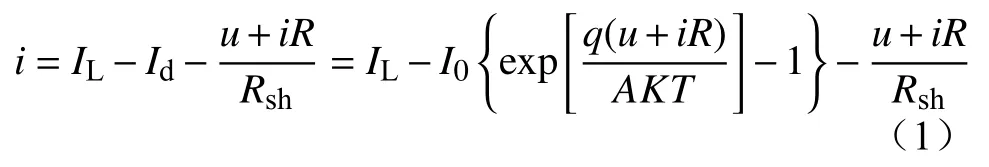
式中：IL为光电流；I0为反向饱和电流；q为电子电荷(1 .69×10−19C)；A为二极管因子；K为玻尔兹曼常数(1 .38×10−23J/K)；T为绝对温度；R为串联电阻；Rsh为并联电阻。

通常仅需要确定参数光电流IL、反向饱和电流I0、二极管因子A、串联电阻R以及并联电阻Rsh这五个参数，根据式（1）即可获得该光伏电池对应的i-u特性曲线。但是，由于上述参数受光伏电池温度T以及光照强度S的影响，并且参数确认过程复杂，因此该模型实际应用中使用较少。

为了简化光伏电池i-u特性曲线的获取过程，文献[20]根据光伏电池生产厂家提供产品在标准测试条件下测试获得的开路电压uoc、短路电流isc、最大功率点电压um以及最大功率点电流im等参数，推导了一种适用于工程应用背景的光伏电池数学模型，如图2所示。

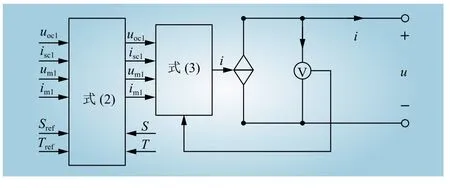
图2 适用于工程应用背景的光伏电池数学模型Fig. 2 Mathematical model of photovoltaic battery for industrial applications

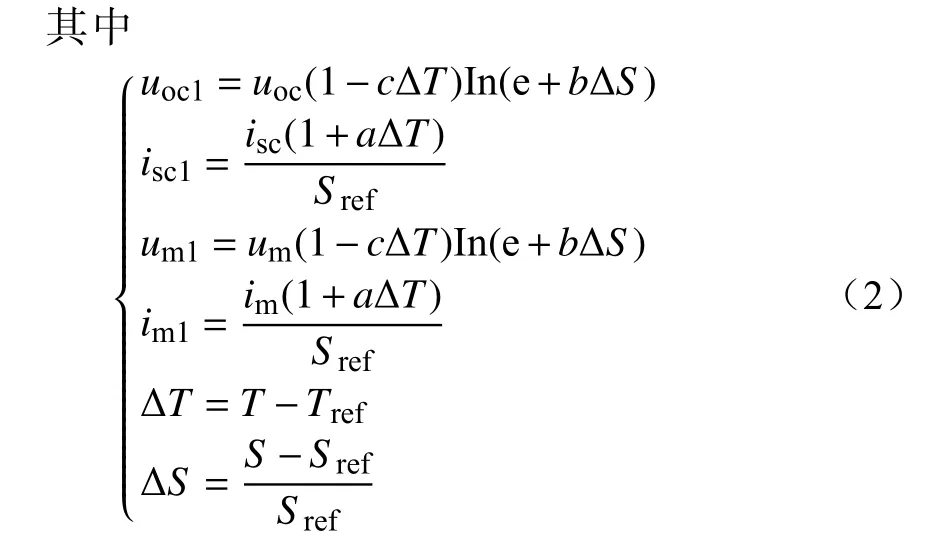
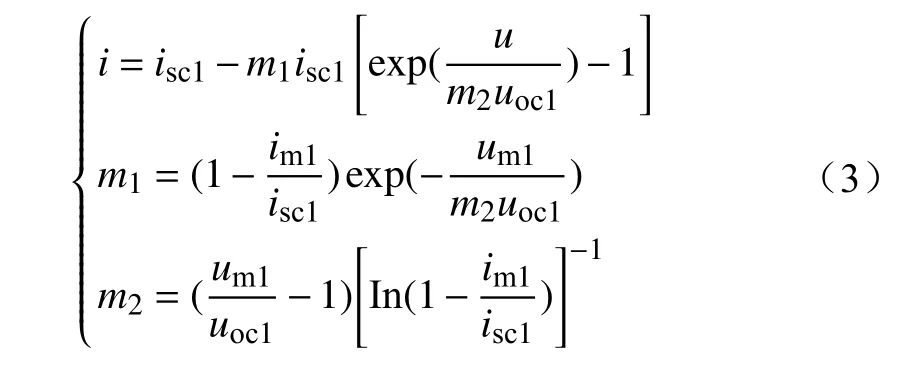
2 单相级联H桥型光伏逆变器的拓扑结构及工作原理

本文以单相级联H桥型逆变器作为研究对象，针对应用于大型光伏发电系统的单相级联H桥型光伏逆变器展开研究，图3给出了单相级联H桥型光伏逆变器的拓扑结构。us和is分别为网侧电压与逆变器输出电流。Ls和Rs是滤波器和线路等效电感与等效电阻。Ci和PVi是第i(i=1，2，···，n) 个H桥对应的支撑电容与光伏阵列。uCi和iPVi是第i个H桥对应的直流侧电容电压和光伏阵列PVi的输出电流。

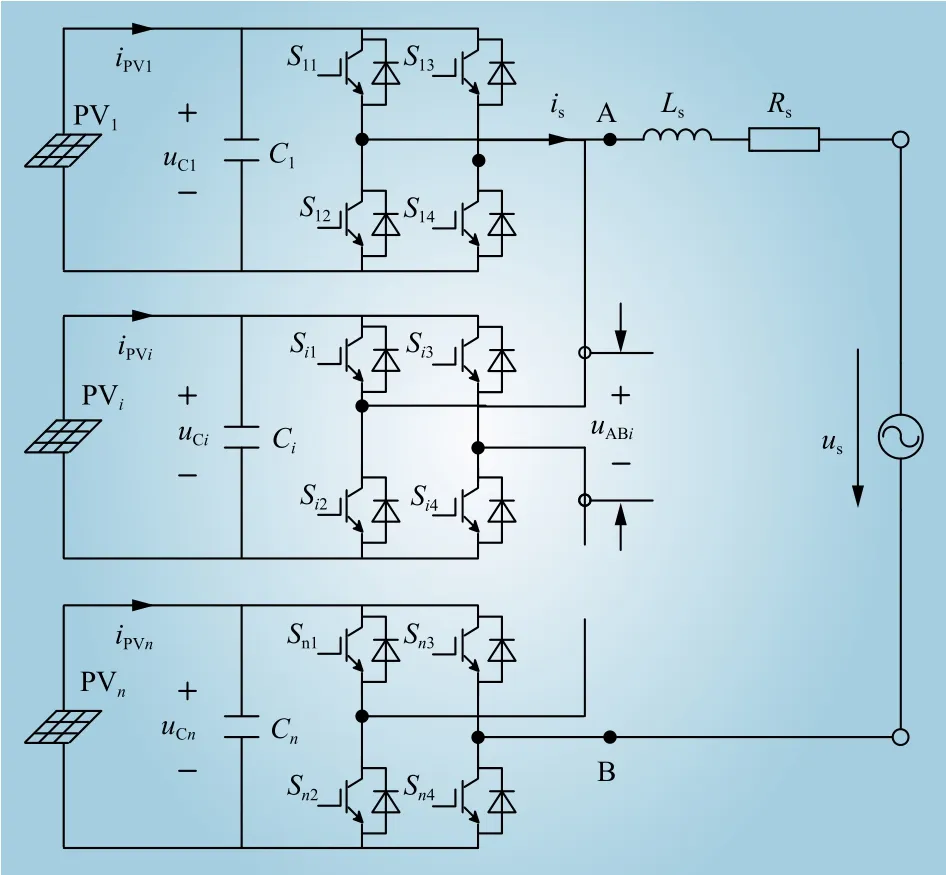
图3 单相级联H桥型光伏逆变器Fig. 3 Single-phase CHB photovoltaic inverter

根据H桥同一桥臂一个开关周期内不允许上、下开关管同时导通的原则，定义第i个H桥的开关函数为

针对单相级联H桥型光伏逆变器，为了对逆变器输出电流is和第i个H桥的直流侧电容电压uCi进行预测，根据基尔霍夫电压和电流定律，对电感Ls两端的电压和流过第i个H桥支撑电容Ci的电流建立微分方程。

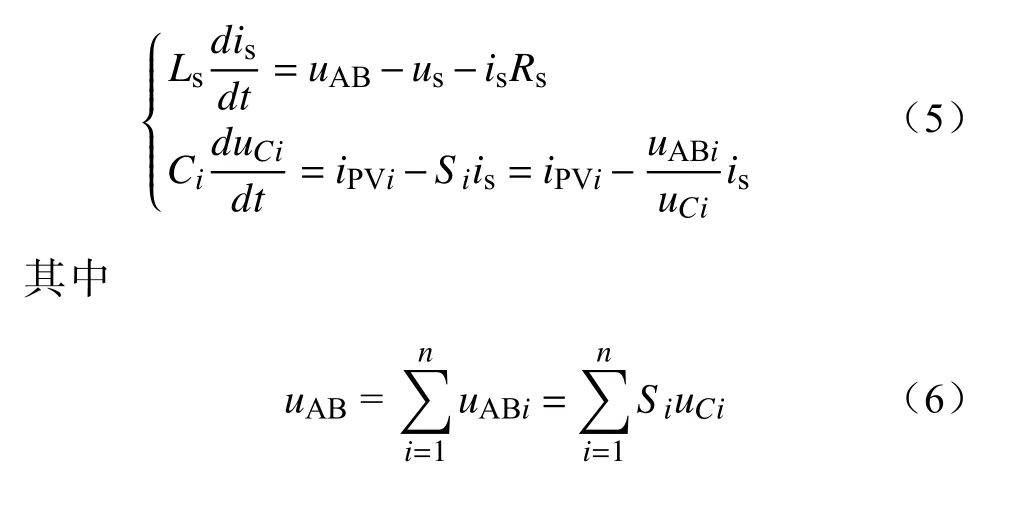
3 直接功率模型预测控制方法

3.1 直流侧电容电压重构原理

定义开关周期Tsw、刷新周期Ts与采样周期Tsc的关系为

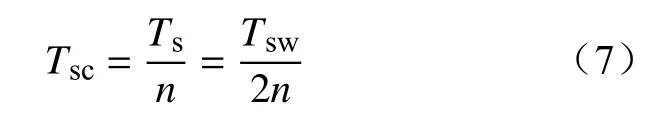
由于单相级联H桥型光伏逆变器控制系统仅对直流侧电容电压的直流分量进行控制，且H桥直流侧支撑电容对直流侧电容电压变化存在着抑制作用，故可将直流侧电容电压视作慢变化量。因此，定义第k个时刻刷新周期内第i个H桥直流侧电容电压重构值为

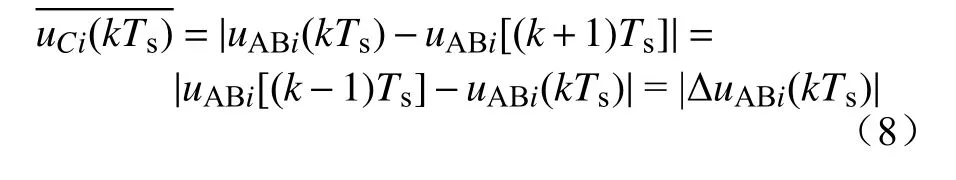
由于无法通过单个电压传感器直接获取单相级联H桥型光伏逆变器各H桥的输出电压uABi，故针对单H桥直流侧电容电压重构算法并不能直接应用于单相级联H桥型光伏逆变器。

为了将该方法进一步用于单相级联H桥型光伏逆变器的直流侧电容电压估计，通过对直流侧电容电压与逆变器输出电压的关系进行详细分析，基于本文给出的模型预测控制时序，可将电容电压重构值定义为单相级联H桥型光伏逆变器输出电压的变化量绝对值。表1给出了针对单相级联H桥型七电平逆变器的各H桥开关函数变化量∆Si与直流侧电容电压重构值uCi的关系。由表1可知，只有当两个相邻采样周期内开关函数Si发生变化时，对应的直流侧电容电压重构值才会发生变化，否则该H桥直流侧电容电压重构值保持不变，即不需要进行重构。

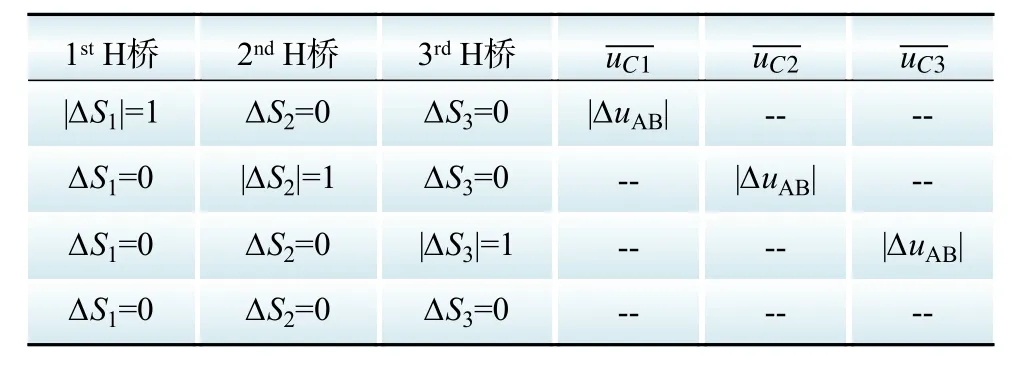
表1 第i个直流侧电容电压重构值与H桥开关函数变化量的关系Table 1 Relationship between estimated value of dc-side capacitor voltage and switching function of the ith H-bridge

根据表1所示的开关函数变化量与H桥直流侧电容电压重构值的关系，图4给出了适用于单相级联H桥型光伏逆变器直流侧电容电压重构算法的工作流程图。以采样周期Tsc为步长对单个H桥开关函数变化量∆Si进行搜索，并选出开关函数变化量∆Si不为零的H桥。针对开关函数变化量∆Si不为零的H桥，则通过计算并网逆变器输出电压变化量 ∆uAB对直流侧电容电压进行重构并按照刷新周期Ts对H桥直流侧电容电压重构值进行刷新，否则保持前一次重构得到的电压值。

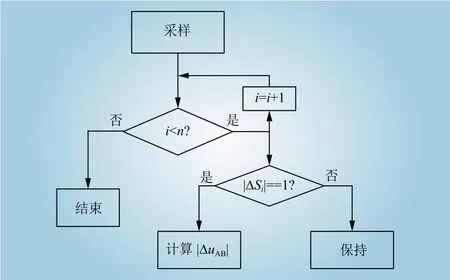
图4 直流侧电容电压重构工作流程Fig. 4 Flow chart for DC-side capacitor voltage reconstruction

3.2 直接功率模型预测控制算法原理

结合图4所示的直流侧电容电压重构算法的工作流程图，图5给出了适用于无直流侧电压传感器单相级联H桥型七电平光伏逆变器的模型预测控制算法的工作原理。基于串行计算模式，该算法的核心思想是将n模块单相级联H桥型逆变器视作n个独立的H桥逆变器，利用时间间隔Tsc，在电力电子开关器件的开关周期Tsw内按照从1到n的顺序串行完成各H桥对应的直流侧电容电压重构、最优调制函数的计算，并按照刷新周期Ts对各H桥的进行直流侧电容电压重构值更新以及最优调制函数计算。

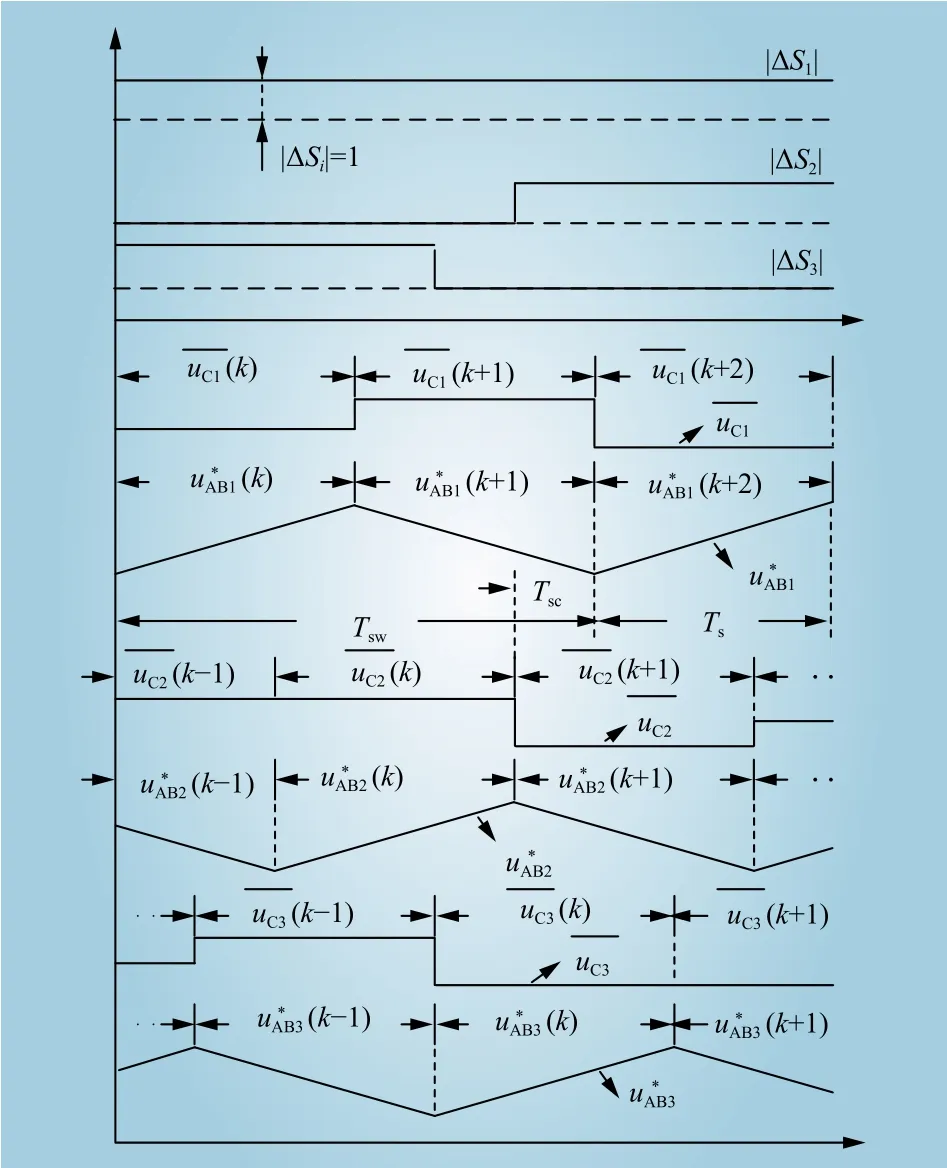
图5 本文所提模型预测控制算法原理Fig. 5 Basic principle of the proposed MPC algorithm

如图5所示，针对第1个H桥，在第k个刷新周期开始时更新最优调制函数。在长度为Tsc的时间间隔内，根据第2个H桥的开关函数变化量∆S2判断是否需要进行直流侧电容电压重构。若需要重构，则根据图4所示流程对其直流侧电容电压进行重构，否则保持重构值不变。然后，利用第2个H桥直流侧电容电压重构值完成第2个H桥对应最优调制函数的计算，并在第2个H桥对应的第k个刷新周期开始时刻输出最优调制函数。以此类推，直到针对第3个H桥完成直流侧电容电压的重构及最优调制函数的计算并输出最优调制函数，则完成了第k个刷新周期的控制过程，并再次从第1个H桥开始进行第(k+1)个刷新周期的控制过程。

基于以上分析，本文所给出的模型预测控制方法的核心思想在于根据图5所示控制时序，以Tsc为计算周期，逐个完成光伏逆变器各H桥对应的最优调制函数计算。同时，在针对单个H桥进行最优调制函数的计算时，结合图4所示流程，实现对各H桥直流侧电容电压的重构。

4 仿真分析

为了验证本文给出模型预测控制方法的正确性及其性能，基于Matlab/Simulink的仿真环境搭建了系统模型，对本文给出的模型预测控制方法与传统电流控制方法进行对比分析。

图6给出了稳态工况下各H桥的重构值与实际值波形。由图6可以看出，各H桥直流侧电容电压重构值与实际值uCi一致，证明文中给出的直流侧电容电压重构方法能够以较高的精度对各H桥直流侧电容电压进行重构。

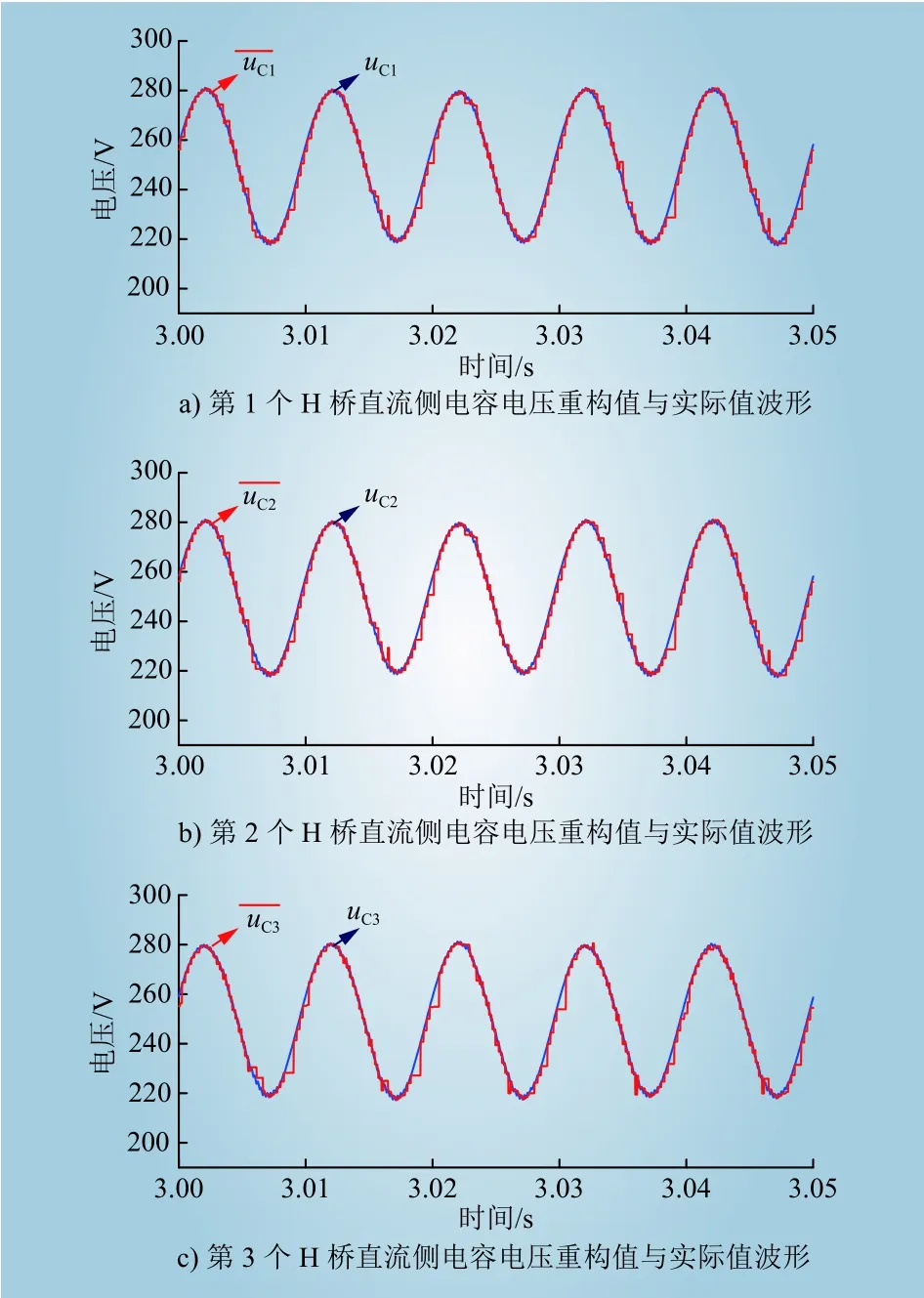
图6 各H桥直流侧电容电压重构值与实际值波形Fig. 6 Waveforms of reconstruction value and real value for DC-side capacitor voltage of each H-bridge

图7给出了基于PI控制器的传统功率控制方法以及本文介绍的直接功率模型预测控制方法在稳态情况下逆变器输出电流与网侧电压波形。根据仿真波形可以观察到，本文介绍的直接功率模型预测控制方法相比于基于PI控制器的传统功率控制方法，其对应的逆变器输出电流波形具有好的正弦性且与网侧电压之间的相位差基本为0。

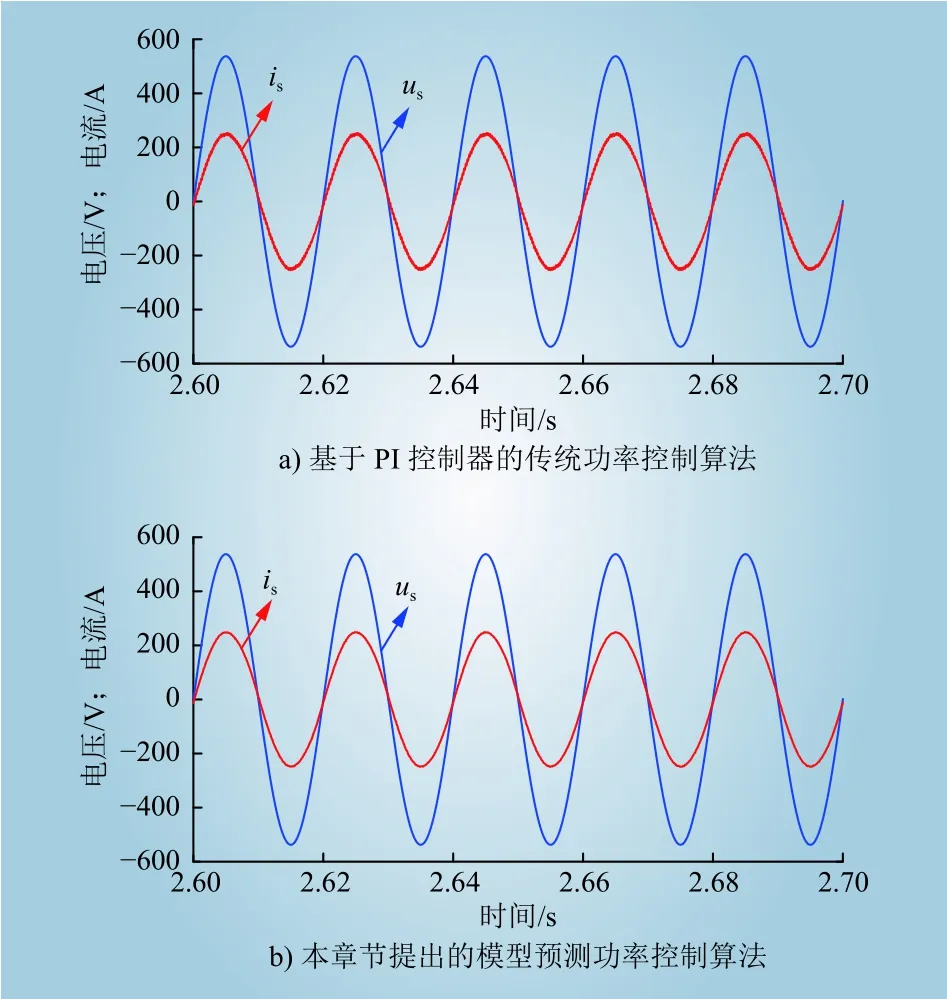
图7 网侧电压与逆变器输出电流波形Fig. 7 Waveforms of source voltage and output current

图8给出了文中介绍的直接功率模型预测控制方法在光照强度变化情况下各H桥（三单元）的直流侧电容电压波形。可以看出，在保证控制系统低复杂度以及低设计难度的前提下，本章节提出的模型预测控制方法能够实现良好的直流侧电容电压平衡效果。此外，在各H桥光照强度不同的情况下所表现的波形幅值不同是由于二次纹波幅值不同造成。

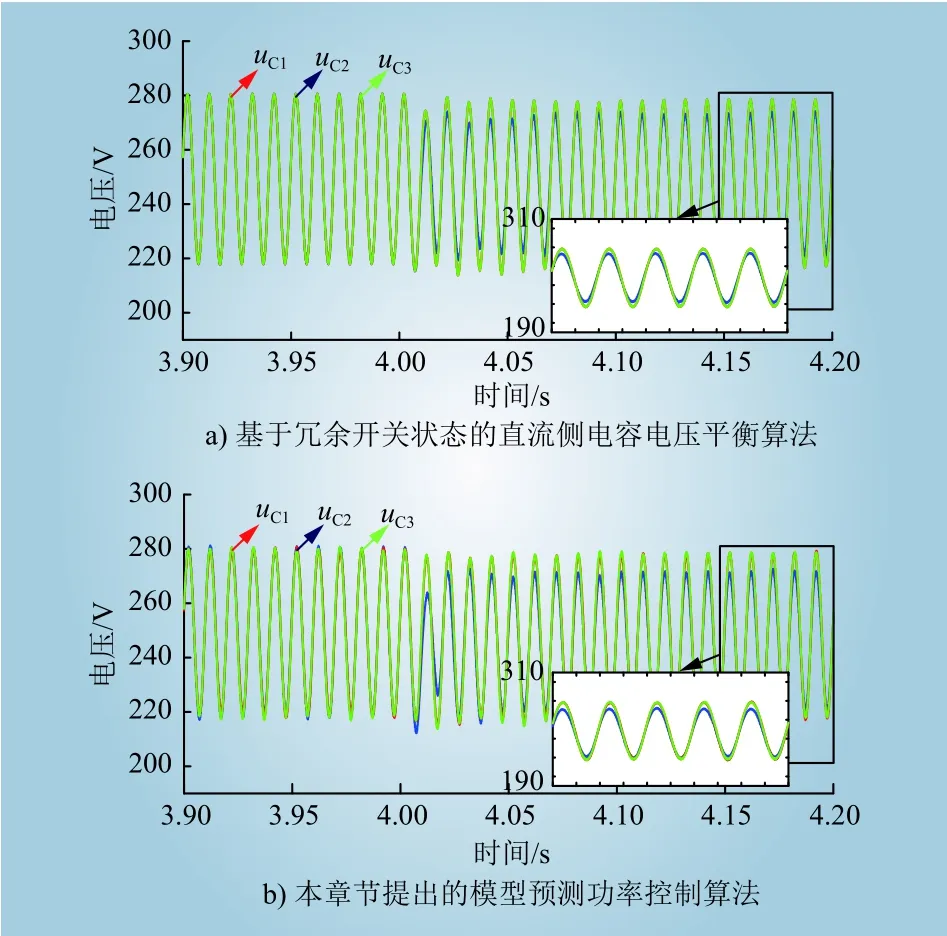
图8 直流侧电容电压波形Fig. 8 Waveforms of DC-side capacitor voltage

图9给出了文中介绍的直接功率模型预测控制方法及基于PI控制器的传统直接功率控制方法对应的逆变器输出电流FFT分析结果。由图9可以观察到，文中介绍的直接功率模型预测控制方法具有更好的谐波频谱，其中高次谐波主要分布在12 kHz频率点附近，更利于低通滤波器的设计。

图9 FFT分析结果Fig. 9 FFT analysis results

5 结语

本文给出了一种适用于无直流侧电压传感器光伏逆变器的直接功率模型预测控制方法。该方法采用串行计算的方式，按照顺序完成针对各H桥的直流侧电容电压重构及最优调制函数计算。同时，通过改变电容电压平衡权重系数的数值可以对电容电压的平衡能力进行调节。

实验结果表明该方法实现了准确的直流侧电容电压估计，取得了良好的稳态、动态性能，并实现了直流侧电容电压的平衡控制。