垂荡板对浮式风机水动—气动耦合性能影响研究

郑建才，赵伟文，万德成, 2

(1. 上海交通大学 船海计算水动力学研究中心(CMHL) 船舶海洋与建筑工程学院，上海 200240; 2. 浙江大学 海洋学院，浙江 舟山 316021)

海上风场相比陆上风场而言，具有平均风速高、湍流强度低等特点，这些丰富的风资源条件为浮式风场提供了良好的经济效益基础。此外，浮式风电产业还能与海上石油和天然气开发等部门形成配套设备，这使得漂浮式风力发电机具有十分广泛的应用前景[1]。然而，由于浮式风机所处海洋环境载荷十分复杂，同时平台受力产生大幅运动响应会增加结构系统的疲劳载荷[2]，且浮式风机作业时水动力和气动力之间耦合效应显著，因此如何抑制浮式风机水动力响应，提升风机风能利用率便成为了浮式风机领域的研究重点。垂荡板作为一种安装在浮式平台上的被动抑制装置，具有能增加浮式支撑平台附加质量，进而增大固有频率的优点，因此被广泛使用在单立柱式Spar平台[3]、张力腿平台[4]以及半潜式平台[5]。

垂荡板不仅能够减小浮式支撑平台的大幅运动，还能影响浮式风机水动—气动耦合后的气动性能，很多国内外的相关学者都对该问题进行了研究。Tao和Dray[6]对带垂荡板的单柱式支撑平台进行了水池试验，试验结果表明垂荡板能够减小原始平台的垂荡和纵摇运动响应幅值，这说明垂荡板能够有效抑制浮式平台的运动响应。而水池试验与数值模拟相比，代价昂贵且受限于试验设备，不能进行垂荡板结构参数研究，如垂荡板安装位置、形状、以及开孔大小等。黄志谦等[7]采用Fluent商业软件对不同垂荡板模型进行数值模拟，对比分析了不同分形阶数以及规则孔垂荡板的水动力特性，研究结果表明附加质量系数随分形阶数增加而减小，阻尼力系数值随分形阶数增加而先增大后减小，且当透空率相同时，分形孔阻尼力系数较规则孔有较大提升。Moreno等[8]采用CFD方法研究了垂荡板对浮式平台运动响应结果的影响，并将数值模拟结果与试验数据进行比较，研究结果表明数值模拟结果与试验结果拟合良好，但是该数值模拟并未考虑风机气动性能的影响。Ding等[9]采用等效力模型进行了垂荡板抑制作用的研究，研究结果表明在等效气动载荷的作用下，垂荡板仍能有效抑制平台的运动响应结果。但是等效气动载荷的方法是一种理想化模型，且未能考虑风轮旋转效应以及平台与风机之间耦合效应的影响，有必要进行浮式风机气动—水动耦合影响下垂荡板的作用分析。Tran等[10]基于叶素动量理论结合三维势流理论，使用FAST开源软件进行了带垂荡板浮式风机耦合性能的分析，研究发现垂荡板一方面能够减小平台的运动幅值，另一方面则增加了风机的输出功率，由于势流理论未考虑水的黏性效应，叶素动量方法也不能进行风机后方的尾流场计算，因此有必要进一步采用CFD方法进行带垂荡板浮式风机气动—水动—系泊耦合性能数值模拟。

目前已经有不少浮式风机采用垂荡板装置的实际案例[11-12]，这表明垂荡板对浮式风机系统具有实际的工程意义。基于开源工具箱OpenFOAM，将非稳态致动线模型嵌入两相流CFD求解器naoeFOAM-SJTU，形成浮式风机水动—气动耦合求解器FOWT-UALM-SJTU，并基于该求解器进行平台水动力、风机气动载荷和锚链系泊载荷三者的耦合计算，并在此基础上分析了垂荡板的形状对浮式风机耦合响应的影响。

1 数值方法

1.1 非稳态致动线模型

致动线模型(actuator line model, 简称ALM)[13]是使用具有等效体积力的线代替风机叶片的方法，在进行流场计算时，不需要求解叶片表面边界层，从而提升了计算效率。在致动线模型中假定风机叶片沿径向分割为若干叶素，并使用致动线上的点代替叶片在该位置处的叶素，若已知每个叶素的弦长c和宽度dr，则该致动点处的受力可以根据该处攻角α对应的升力系数Cl、阻力系数Cd和相对于叶片的流速Urel求解得出。

在初始致动线模型中，旋转叶片相对于叶片的流速Urel矢量关系如图1所示。其中在进行浮式风机水动力和气动力的耦合传递过程中，需要在此基础上附加由于平台运动引起的非稳态速度UM，形成非稳态致动线模型(unsteady actuator line model, 简称UALM)。

图1中，Ω是旋转角速度，UZ和Uθ分别是轴向和切向速度，UM,Z和UM,θ分别是平台诱导速度在轴向和切向的分量。则该叶素处的相对速度大小Urel为：

(1)

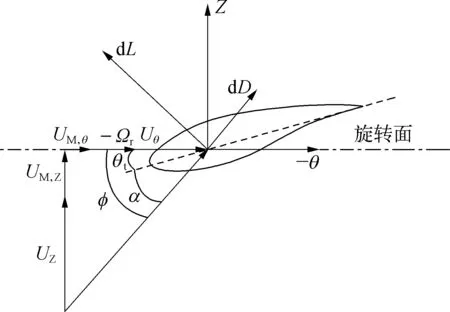
图1 叶片截面上速度矢量图Fig. 1 Velocity triangle on a local blade section

若已知致动点处的α，Cl，Cd，并基于上式求得该点的相对速度Urel，可得到每个致动点上产生的力f。但是每个致动点处产生的力f为一系列离散的点力，这些点力并不能直接作用于流场中进行计算，以避免数值发散，需采用高斯权函数将反作用于流场体积力进行光顺。

(2)

(3)

其中，(xi,yi,zi)是第i个致动点，di是点(x,y,z)与点(xi,yi,zi)之间的距离,ε称为高斯光顺参数。为了保证数值稳定性，文中取ε≈2Δx(Δx为叶片附近网格单元的长度)。Troldborg等[14]指出，2Δx是防止在应用空间中心差分格式时速度场出现数值振荡的最小值。

1.2 气动—水动耦合模型

将上述非稳态致动线模型嵌入气液两相流求解器naoeFOAM-SJTU，形成浮式风机气动—水动耦合求解器FOWT-UALM-SJTU，同时考虑到大涡模拟方法(large eddy simulation, 简称LES)在捕捉非平衡、非稳态结构时的大尺度效应的优越性，因此在该数值模拟中采用大涡模拟方法进行浮式风机气动—水动耦合计算，其控制方程：

(4)

式中：带“～”符号意为空间过滤，fσ为表面张力项，fs为消波区源项，fε为体积力项。其中Smagorinsky模型被用于求解亚格子应力τSGS：

(5)

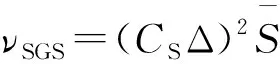
在该求解器中对于系泊力的求解使用的是准静态方法(piecewise extrapolating method, 简称PEM)，与悬链线方程相比考虑了系泊预张力和流体力的影响。对于锚泊作用下的浮式平台的六自由度运动响应通过naoeFOAM-SJTU求解得到，在水动力响应求解时分别采用随平台运动的随体坐标系以及大地坐标系，两者之间的关系如图2所示。通过时间步进行PISO[15]循环求解N-S方程，更新六自由度运动引起的致动点的速度分量UM，并将求解得到的速度分量传递给非稳态致动线模型。与此同时受平台运动影响后的风机气动载荷也反馈到系泊系统作用下的平台运动方程中，进而实现浮式风机气动—水动耦合求解。综上所述，使用FOWT-UALM-SJTU进行浮式风机气动—水动耦合求解流程如图3所示。

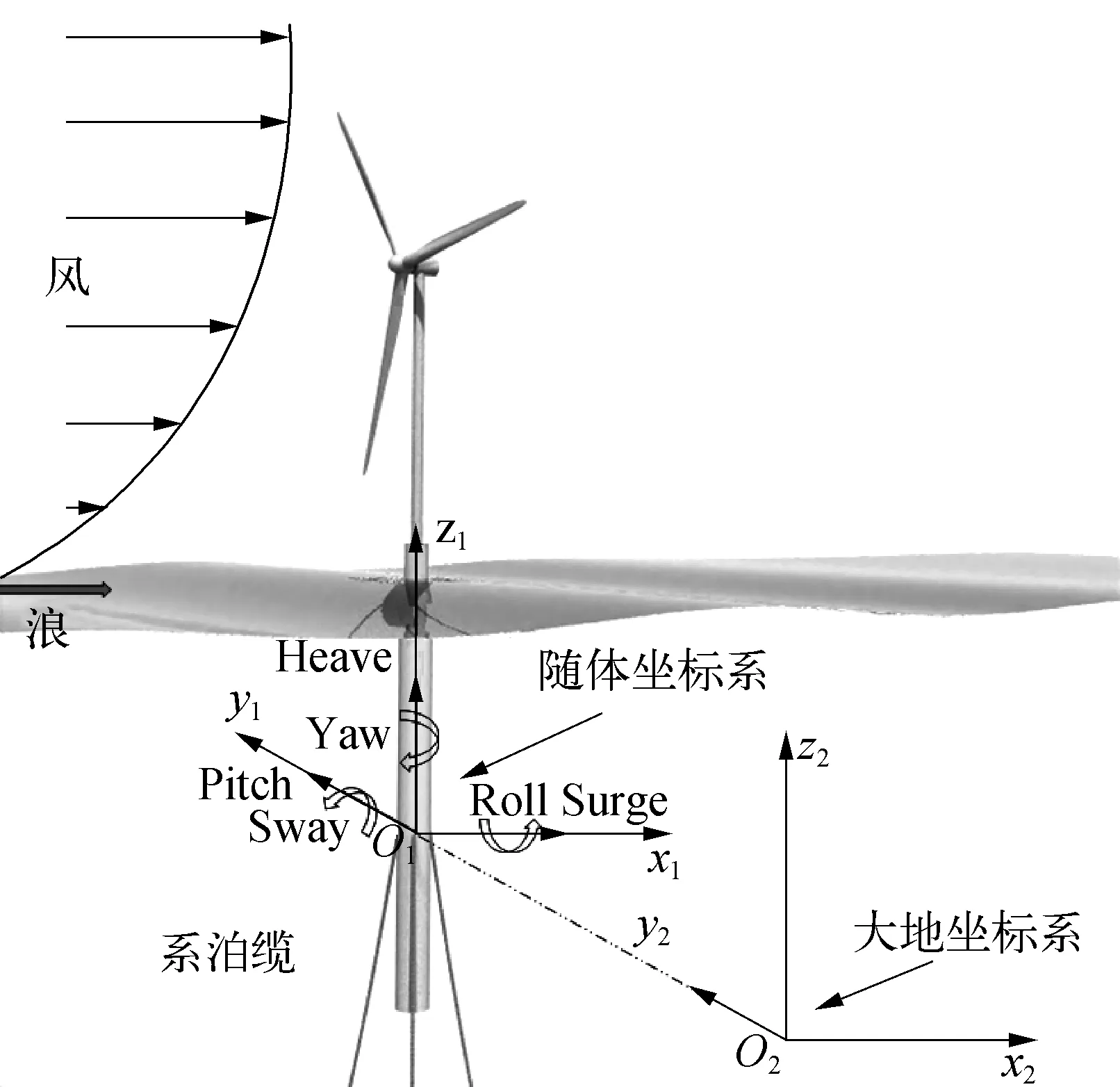
图2 六自由度运动响应坐标转换示意Fig. 2 Two coordinate systems in solving motions equation of floating platform

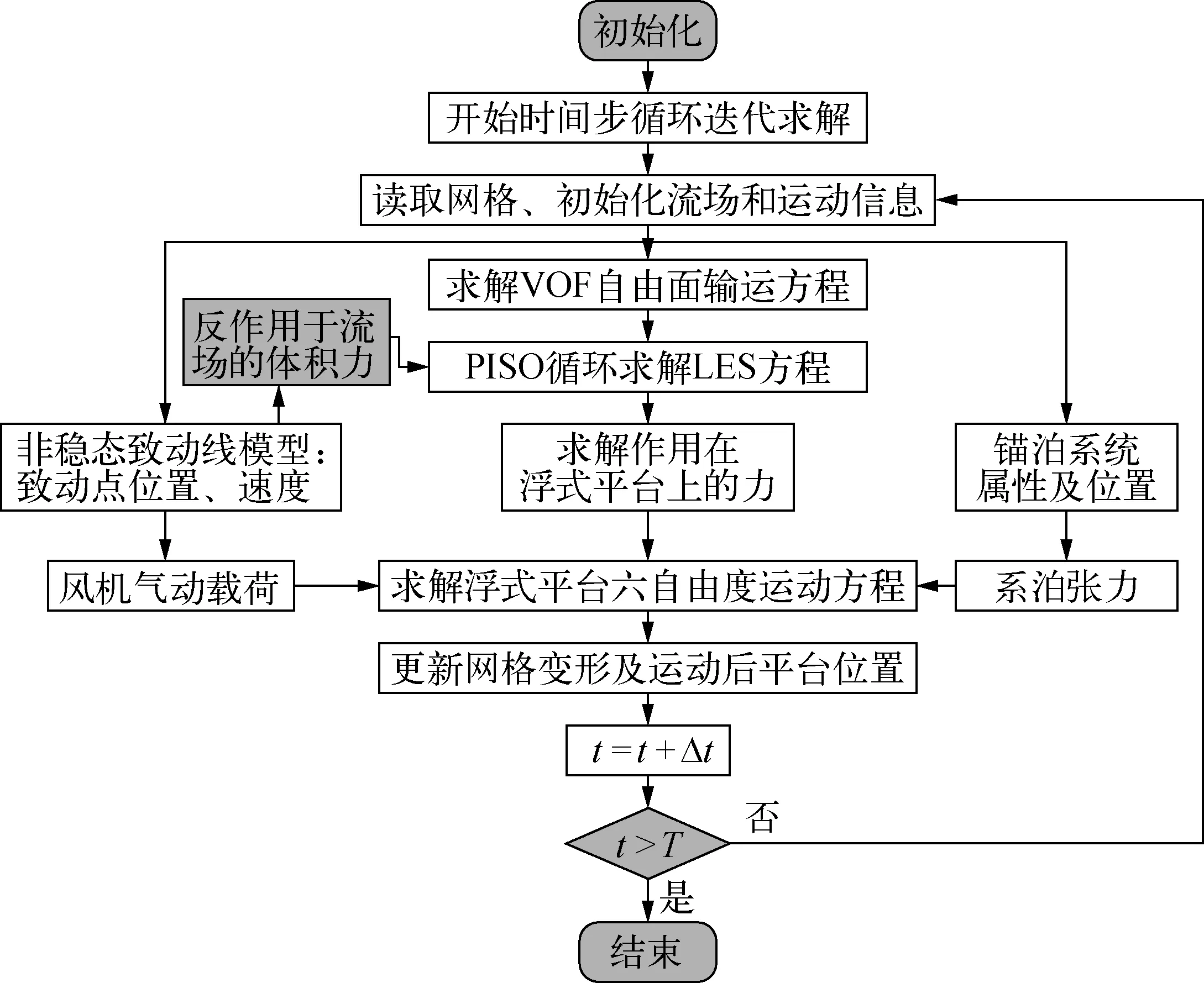
图3 浮式风机气动—水动耦合求解流程图Fig. 3 Flow chart of solving strategy of coupled aero-hydro simulation

2 计算设定

采用的浮式风机模型由美国国家能源实验室的NREL-5 MW[16]风力机和OC3-Hywind Spar浮式平台组成。为了研究垂荡板对浮式风机耦合性能的作用效果，需要确保相同的波浪载荷，同时还需要考虑风剪切效应对风机气动性能的影响。因此在进行数值模拟时，参考Jonkman等[17]的工作，设置规则波波高为6 m，波浪周期为10 s；轮毂高度H处风速为U0=11.4 m/s，且不同高度位置Z处风速UZ服从指数规律：

(6)

分别设置三个算例进行不同形状垂荡板对浮式风机气动—水动—系泊耦合性能的影响分析，其中带圆形和正方形垂荡板的浮式平台模型如图4(b)～(c)所示，三个算例采用的数值计算模型参数如表1所示，其中垂荡板的直径、厚度参考文献[18]，垂荡板的吃水位置在-130 m处。

图4 数值计算模型Fig. 4 The model of numerical simulation

表1 算例设置

设置以上算例的计算域如图5所示。其中风轮旋转平面的中心距离入口处1.25D，风机后方沿流向长度为3D，计算域的宽度为3D，轮毂高度以上为1.5D，为了避免水深对平台运动造成的干扰，沿水深方向设置为1.7d(如图5所示，D为叶片直径，d为平台吃水)。同时为了进行致动线附近网格的插值计算并较好地捕捉尾流中的涡结构，在风机后方区域使用两级网格加密，一级网格加密区域的宽为1D，高度从自由面处至轮毂高度上方1D；二级网格加密区域分别在宽度和高度方向上减小0.2D；考虑到风机后方的螺旋状尾涡在黏性作用下的延伸及膨胀现象，加密区域一直延伸至出口边界。在数值计算中，基于开源平台OpenFOAM，使用自定义求解器FOWT-UALM-SJTU进行浮式风机气动—水动全耦合数值模拟，设置入口为三维数值造波边界条件，物面为移动壁面边界条件，三个算例的网格总量分别为308万、368万和367万。

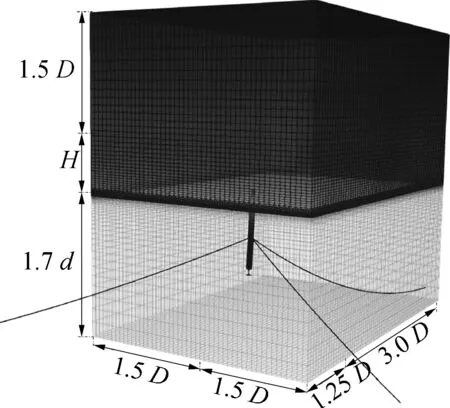
图5 计算域布置Fig. 5 Sketch of computational area

在求解器正确性验证方面，Li等[19]通过使用FOWT-UALM-SJTU求解器，在相同条件下对不同俯仰运动幅值下的瞬态气动功率和推力计算结果进行数值模拟，并与Tran等[10]采用star-CCM+商业软件中的非定常叶素动量理论进行的多自由度数值模拟结果进行对比，结果表明该求解器能够满足浮式风机气动—水动耦合问题的求解精度。

3 结果与分析

3.1 气动载荷

观察风力机的气动功率时历曲线(图6)可知，在耦合运动影响下，功率波动周期与平台发生的纵摇波频运动周期相同，但带垂荡板浮式风机系统气动功率达到稳定平衡的时间相对提前。这是由于垂荡板的阻尼作用，使得平台的纵摇运动响应稳定时间提前，而风力机的平台运动和气动载荷相互耦合后，风力机的输出功率主要受纵摇运动影响。

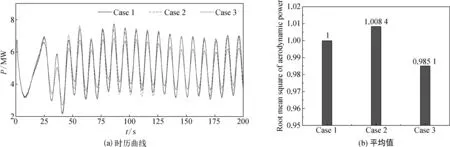
图6 气动功率性能Fig. 6 The performance of aerodynamic power

此外由于垂荡板的作用，气动功率在初始时刻和稳定时刻幅值相应增大。这是由于在初始时刻，带垂荡板的浮式支撑平台会提供一个较大的水动力阻尼力以抵消风机产生的气动推力，这提升了浮式风机系统在深远海抵抗湍流风的性能。而当功率趋于稳定时，此时纵荡和垂荡运动响应幅值降低，浮式风机处于更加稳定的动态平衡状态，因此气动功率会相应增加。将气动功率的结果进行时均化处理可知，带圆形垂荡板的浮式风机系统功率提升约0.844%，而带正方形垂荡板却使得平均功率减小1.492%。由此可见对气动功率的提升而言，圆形垂荡板的效果优于正方形。

为了进一步区分圆形垂荡板与正方形垂荡板作用效果的差异，将两者的功率结果进行快速傅里叶变换并取模，并将横坐标轴无量纲化为斯特劳哈尔数得到功率频谱如图7所示。从图7中可以看到，圆形垂荡板会增大气动功率在St=0.221(fr=0.02) 外的幅值，即气动功率波动幅度增大。

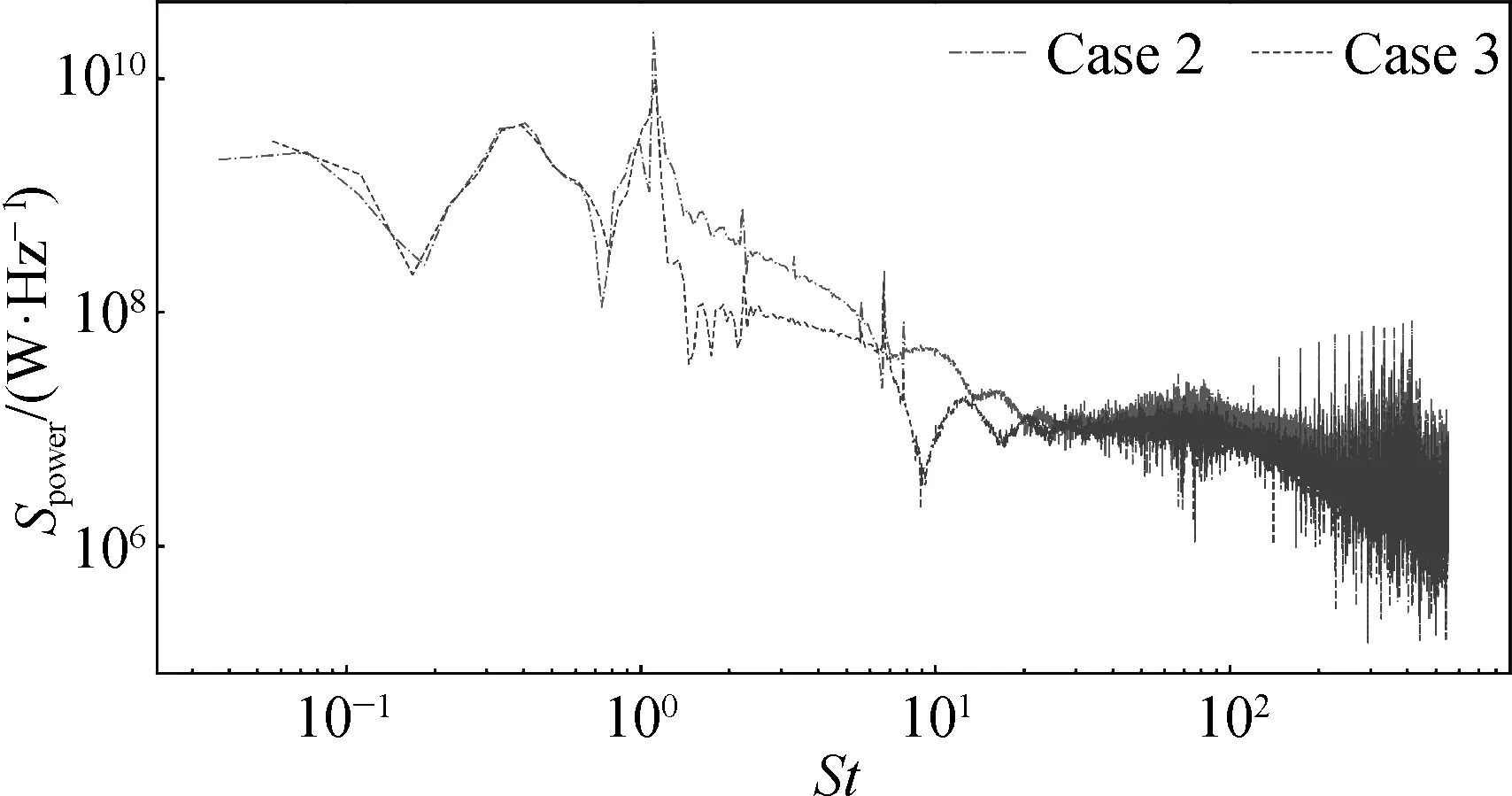
图7 浮式风机机械功率频谱Fig. 7 Spectrum of power output of FOWT

在非稳态致动线模型中，气动载荷是根据叶片攻角对致动点处的升阻力系数进行插值求解，从而得到反作用于流场的体积力。在垂荡板的作用下，浮式风机系统的波频运动随之改变，进而会影响风机叶片翼型攻角的变化。图8分别给出了采用不同计算模型时风机叶尖处翼型攻角的时空云图(考虑攻角周期性变化，图中给出40 s内攻角随时间和空间变化的云图)。由图8可知垂荡板能够明显地增大0.45r～0.95r之间的翼型攻角，这有利于风能的吸收，有助于提升风机气动功率。此外，四个波浪周期内带圆形垂荡板浮式风机叶尖处攻角的平均值比带正方形浮式风机大0.002°，即在相同直径时圆形垂荡板增加翼型攻角的作用优于正方形，但总体相差并不大。

图8 叶片攻角时空云图Fig. 8 Contour of attack angle of blades

此外在进行风机的气动载荷分析时，均方根值(root mean square，RMS)能够代表气动结果的有效性，表示载荷值的大小，而标准差(standard deviation，STD)能够指出气动结果随时间波动的剧烈程度，值越大表示疲劳载荷越大。

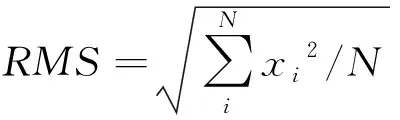
对风机的轴向弯矩和切向弯矩分别进行分析如图9所示。其中带圆形垂荡板浮式风机系统的轴向弯矩的均方根值相对增大0.404%，而切向弯矩的均方根值相对减小0.595%，两者的标准差减小都在4.5%以内。而带正方形垂荡板轴向弯矩和切向弯矩均方根值分别减小0.595%和3.075%，两者的标准差减小都大于30%。这说明附加圆形垂荡板的浮式风机能在保持疲劳受力的条件下，增大浮式风机捕获风能的效率。相对而言，虽然带正方形垂荡板的浮式风机系统气动载荷波动较小，但其气动载荷的值也降低较大，并不利于对气动功率的提升。

图9 风机旋转过程中受力及误差分析Fig. 9 Moment of turbine during rotation

3.2 水动力响应

在进行风浪联合作用下浮式风机耦合性能研究时，运动响应与平台固有周期、波浪频率以及风轮旋转周期等多种因素相关，这一方面会影响平台的水动力性能，另一方面还会影响水动—气动耦合后的气动力性能。图10给出了浮式风机耦合状态下平台运动响应随时间的变化曲线。对整个波浪周期内的运动响应结果统计可知，带圆形和正方形垂荡板平台的纵荡运动响应幅值分别相应减小23.339%和6.255%。这是由于垂荡板增大了平台的水动阻尼力，使得系泊系统作用下的纵荡运动幅值相应减小。带圆形垂荡板和正方形垂荡板平台的垂荡运动响应幅值分别减小25.637%和30.524%，这主要是垂荡板增大了浮式风机系统的质量力和阻尼力的影响，进而使得平台的垂荡板运动响应幅值减小。

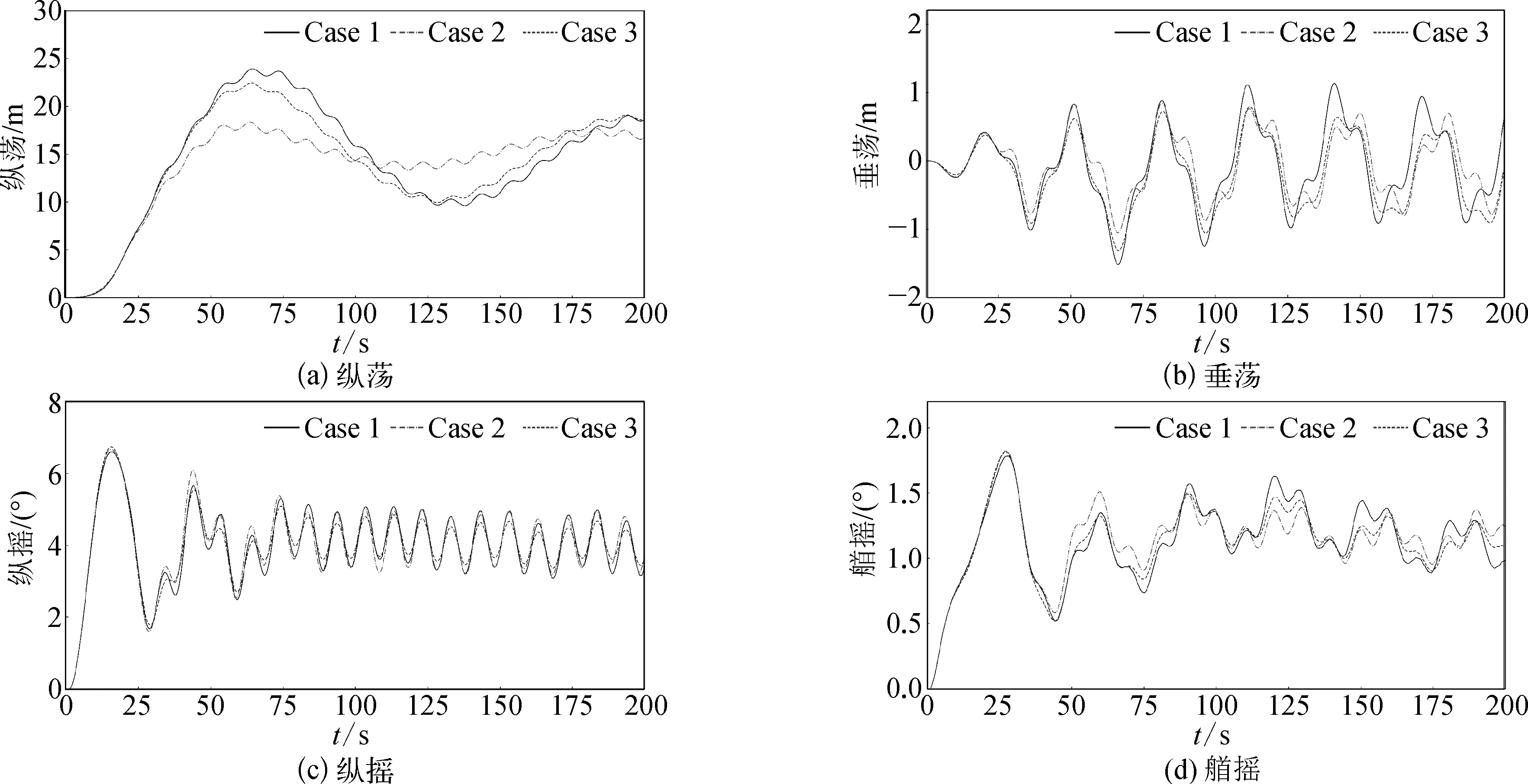
图10 平台运动响应Fig. 10 Motion responses of platform

为了分析两种形状的垂荡板对垂荡运动响应的影响，对其结果进行快速傅里叶变换如图11所示，由图可知圆形垂荡板能明显减小平台在垂荡固有频率处的运动响应幅值，但在波浪诱导频率f=0.1 Hz处的幅值却较正方形垂荡板增大。这是由于当考虑风机和平台的耦合作用时，风力机受到的气动载荷会传递到平台上，因此平台不仅会受到波浪载荷的作用，还需要承受到由风力机传递的气动载荷，这是两者产生耦合后共同作用的结果。此外由于风剪切效应和偏航力矩的存在，Spar平台存在较大的艏摇运动响应，由于垂荡板的存在，使得带圆形垂荡板和正方形垂荡板平台的艏摇运动响应平均值分别减小2.006%和1.955%。而垂荡板对纵摇运动响应结果并无明显作用，在系统处于稳定平衡状态时，带圆形垂荡板系统的纵摇运动响应平均值反而增大了0.439%，而带正方形垂荡板纵摇运动平均值减小0.072%。

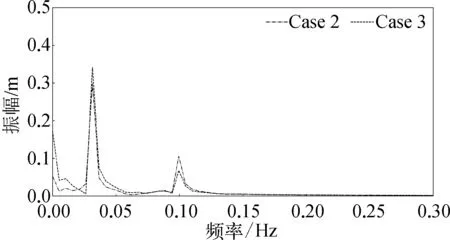
图11 垂荡运动响应傅里叶变换结果Fig. 11 Result of heave motion with FFT transform

在进行浮式风机气动—水动耦合计算时，浮式风机的动态平衡基于风机的气动载荷、平台的水动力载荷以及系泊系统的系泊载荷三者的共同作用。采用分段外推法进行系泊缆的受力分析，系泊缆张力随时间的变化规律如图12所示。由图12可知，系泊缆绳的总张力变化趋势和平台的纵荡运动趋势相似，这是由于张力变化主要取决于平台纵荡运动响应结果。同时，由于纵荡和纵摇运动响应之间的耦合效应，系泊张力呈现小幅度周期性波动。对比可知，初始时刻带垂荡板浮式风机受到的系泊张力与不带垂荡板浮式风机系泊张力相同，这是为了保证系泊缆在初始时刻具有相同的预张力，并在整个计算中尽量保证系泊系统的静回复力刚度一致。此后由于浮式风机受到风浪载荷的联合作用，开始偏离平衡位置，此时由于垂荡板增加了浮式平台的阻尼力，因此系泊缆产生一个较小的系泊张力即可维持系统的动态平衡位置。此外由于带垂荡板浮式风机系统系泊载荷波动周期随之减小，此时应注意系泊缆疲劳载荷，避免因系泊缆疲劳载荷引起的系统失效。

图12 系泊张力时历曲线Fig. 12 Time history curves of mooring tension

3.3 尾流场

沿流向中纵平面的尾流速度场和涡结构组合如图13所示。由图可知，风浪联合作用下入流风通过风轮后，尾流速度明显降低，且速度亏损主要集中在风轮后方叶片中间对应的位置。同时由于风剪切效应的存在，风轮后方的不对称性相应增加。此外随着流向距离增大，风机后方的尾流宽度逐渐增大。

图13 沿流向中纵平面的轴向尾流速度场与尾涡结构组合Fig. 13 Axial direction wind velocity combined with the wake vortex structure contours in the longitudinal section in center plane

在相同的风浪条件下，带垂荡板浮式风机的尾流速度场略微小于不带垂荡板的浮式风机，但三者之间的尾流速度场和涡结构总体差异不大。这说明在垂荡板的作用下，虽然支撑平台的水动力性能得到了改善，但风机系统的气动功率并不一定增加。

4 结 语

使用浮式风机气动—水动耦合求解器FOWT-UALM-SJTU，基于大涡模拟方法，针对带垂荡板的OC3-Hywind Spar平台与NREL 5 MW风机组成的浮式风机系统进行了耦合性能计算，并对其数值结果及垂荡板作用下气动—水动耦合性能变化的原因进行了分析。此外，对比分析了相等直径时，圆形和正方形垂荡板的作用效果。研究结果表明：相等直径和吃水位置时，圆形垂荡板能使该浮式风机的平均气动功率增大约0.844%，且圆形垂荡板对浮式风机系统的作用效果优于正方形；带圆形垂荡板的浮式风机系统轴向弯矩载荷增大0.404%，切向弯矩载荷减小0.595%，且两者的标准差增大都保持在4.5%内，这说明带圆形垂荡板浮式风机能在满足疲劳载荷增加不大的条件下，增大风轮的捕获效率；圆形垂荡板使得纵荡和垂荡运动响应幅值分别减小23.339%和25.637%，正方形垂荡板使得纵荡和垂荡运动响应幅值分别减小6.255%和30.524%；在稳定平衡阶段，带圆形垂荡板浮式风机纵摇平均值增大了0.439%，而带正方形垂荡板浮式风机纵摇运动响应平均值减小了0.036%。

从数值计算结果可知，基于CFD技术和非稳态致动线模型进行带垂荡板浮式风机气动—水动—系泊耦合性能的研究，能够给出精细的浮式风机气动载荷、水动力载荷和风机后方尾流场的数值模拟结果。这说明圆形垂荡板是一个增强浮式风机系统稳定性的可行方案，且为浮式风场的数值模拟及布置优化提供了支撑。