门式起重机主梁疲劳寿命预测研究
沈奕成
(上海航天电子技术研究所,上海 201108)
0 前言
随着工业化进程不断加速,起重机日益成为机械、造船、冶金等重大行业生产过程中必不可少的设备。主梁作为起重机的核心部件,在其工作过程中,受到随机的交变载荷作用。长期反复的载荷作用可能引起主梁结构损伤,甚至是疲劳失效,给工作人员带来巨大的安全隐患和直接的经济损失[1-2]。因此,对门式起重机主梁疲劳寿命预测具有较强的现实性和迫切性。
近年来,国内外一些学者在疲劳领域进行了深入的研究,并取得了显著的成果。Grondi[3]通过现场实测的方法,观察记录箱型梁的拐角裂纹,然后假设法兰裂纹的增长速率与腹板裂纹的增长速率一致,使用断裂力学理论进行疲劳寿命计算。李振华[4]用Miner公式和等效应力法分别计算了焊接箱形梁的寿命。Ozden Caglayan[5]等通过对起重机进行现场检测,然后根据实际采集的数据修正基于Ansys分析的有限元模型,最后利用修正后的模型对起重机寿命进行预测。龙靖宇等[6]运用多体动力学软件Adams建立起重机虚拟样机模型,并对起重机的运作过程进行了动态仿真,最后根据仿真结果进行疲劳寿命预测。
本文针对门式起重机的运行工况,采用有限元软件进行静力学分析,同时结合绘制的载荷谱,利用nCode Design-Life软件对其疲劳分析,预测起重机的使用寿命。
1 有限元静强度分析
1.1 有限元简化模型的建立
在有限元分析中,考虑硬件设备的配置,为了加快计算速度,获得较精确的计算结果,将复杂的几何模型转化成易于分析的简化模型。
(1)针对主梁作为研究对象,省略了螺纹、螺丝等细微部件。
(2)将主梁作为刚体进行模拟,降低运算的难度。
(3)简化了电机、吊钩、钢丝绳等结构。
起重机参数如表1所示,使用Solidworks对门式起重机建模,如图1所示。

表1 门式起重机各截面尺寸及主要技术参数表
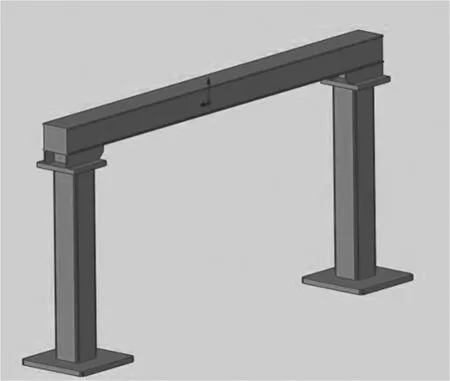
图1 门式起重机有限元简化模型
1.2 有限元静力学分析
根据门式起重机的工作过程,选取了2种典型位置加载荷进行静应力分析。主梁中间位置起吊3 000 N的重物和左侧支腿处起吊3 000 N的重物。
在Patran中分别对有限元模型添加相应位置的前处理操作,然后用Nastran进行求解,然后对求解结果进行后处理与结果显示。最终所得各位置的等效应力云图、位移云图如2~4所示。

图2 主梁中间位置等效应力云图

图3 主梁中间位置位移云图

图4 左侧支腿处等效应力云图
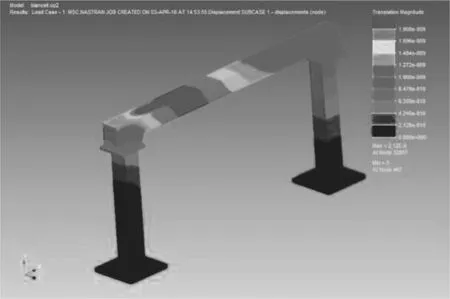
图5 左侧支腿处位移云图
从仿真分析的云图可以看到:主梁的中间位置是危险点,受到最大应力,为130 MPa。将梁中间位置的有限元静应力结果用于疲劳分析。
对于弹塑性材料许用应力为[σ]=σs/n,其中,σs为材料的屈服极限;n为安全系数。由Q235钢的屈服极限为235 MPa,根据起重机设计规范[7]取安全系数n=1.34,可得该起重机的许用应力为175 MPa,满足强度要求。最大变形仅为3.598×10-5mm,满足刚度要求。
2 起重机的疲劳寿命预测
2.1 疲劳分析五框图
疲劳类型分为高周疲劳(应力疲劳)和低周疲劳(应变疲劳)。出于安全考虑,起重机往往具有较大的安全裕度,这使得起重机经常工作在低应力场合,具有较长的寿命周期,因此门式起重机的疲劳属于高周疲劳。故本文采用S-N方法对其进行疲劳分析。
本文基于有限元静力学结果进行疲劳分析的思路,得出门式起重机疲劳分析流程图。如图6所示。

图6 疲劳分析五框图
2.2 载荷谱的获取
疲劳分析载荷谱的编制非常关键,对疲劳寿命的预测具有重要影响。通常载荷谱是靠实验测试获取的,由于实验条件限制,又为了能真实的分析门式起重机的疲劳失效,本文采用运动仿真软件Adams对起重机多个典型工况进行模拟,如表2所示,增加了疲劳寿命预测的可靠性。其中,使用Adams/cable模块对滑轮组与钢丝绳建模,如图7所示。

表2 典型工况表
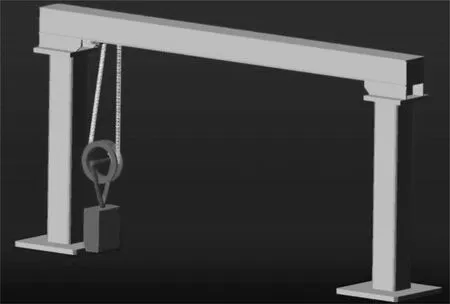
图7 运动仿真模型
根据运动仿真,获得相应工况下的载荷时间历程曲线,如图8~10所示。
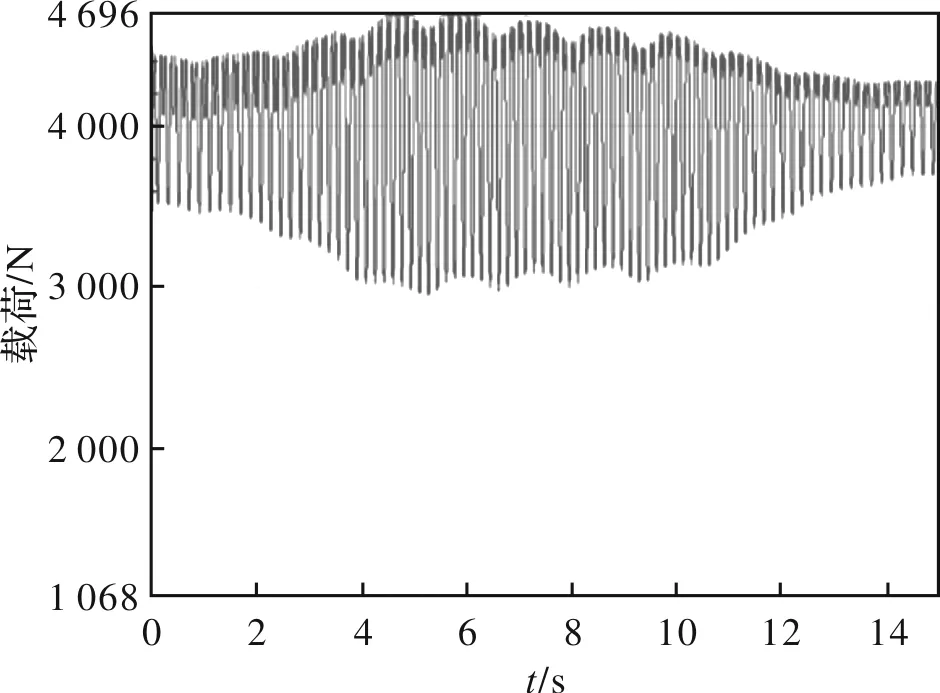
图8 工况1的载荷时间历程

图9 工况2的载荷时间历程

图10 工况3的载荷时间历程
2.3 材料属性设置
Design-Life具有强大的材料库,不仅提供丰富的材料,还支持用户自定义材料。本文中的门式起重机主梁、支腿均采用碳素结构钢Q235材料。其弹性模量2.1×105MPa,材料密度7.89 kg/m3,泊松比0.3。在材料库中定义该材料,并映射到疲劳分析处理模块中。根据定义好的材料属性可以得出材料的S-N曲线。如图11所示。
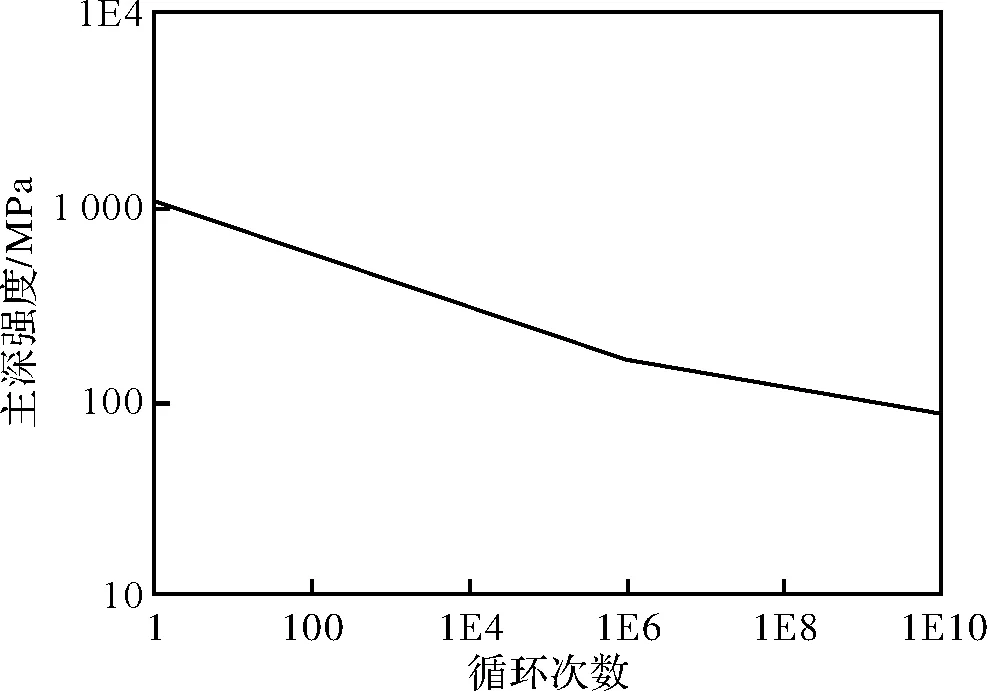
图11 门式起重机材料的S-N曲线
2.4 疲劳寿命分析
在静力学分析的基础上,结合载荷时间历程,导入到nCode Design-Life中进行疲劳分析,分析界面如图12所示。

图12 疲劳分析界面
待各参数设置完成后,开始进行求解,得到工况1下起重机主梁中间位置的疲劳损伤云图和寿命云图。如图13~14所示。

图13 工况1主梁中间位置疲劳损伤云图
从损伤云图和寿命云图可以看出,门式起重机最薄弱的位置是13 843节点处,最大损伤值为1.079×10-6mm,对应的其寿命最小为4.266×107次,即在15 s载荷谱作用下,门式起重机可以安全重复起吊4.266×107次,依据起重机每个月工作30天且每天工作10小时的原则,进行时间转换,可得该起重机寿命为49.375年。从整体寿命云图可以看出,其他绝大多数部位循环均大于9.268×108次,远大于工程中对门式起重机寿命的要求,可得,门式起重机得寿命能充分满足工程安全使用的要求。

图14 工况1主梁中间位置疲劳寿命云图
2.5 多工况下疲劳寿命结果的对比与分析
为了研究起重机在多种工况下的疲劳寿命,依次更换不同工况下的载荷谱进行疲劳寿命的分析,得到起重机主梁中间位置各工况下得疲劳寿命云图如图15~16所示。

图15 工况2疲劳寿命云图
从各工况寿命云图可以看出:
(1)各工况寿命依次递减。由于梁的中间位置所受应力最大,在该位置处频繁的起吊或者降落重物,会增加起重机主梁的损伤,缩短疲劳寿命,符合预期的结果。
(2)总体上讲,三种工况下疲劳寿命虽有所差异,但可允许的疲劳循环次数仍在107数量级内,充分满足工程安全使用的要求。

图16 工况3疲劳寿命云图
3 起重机的裂纹拓展寿命估计
本文研究中默认材料是无缺陷的。可是在实际生活中,构建或者材料中的缺陷是难以避免的。开始无缺陷但是在使用过程中发现了裂纹的构件是否可以继续使用,如何确定含缺陷构件的剩余使用寿命,是疲劳分析的重要问题。
断裂力学中的线弹性断裂力学为研究含缺陷结构的疲劳计算提供了理论基础。本文也是基于该理论求解门式起重机的裂纹拓展寿命,并验证有限元计算结果的可靠性。
3.1 线弹性断裂力学的基本参数
应力强度因子K为构件抵抗低应力脆断破坏能力强弱的指标。其临界值用断裂韧度Kc来表示。平面应变断裂韧度用KIc表示,指的是Ⅰ型裂纹在平面应变条件下的应力强度因子。本文所述应力强度因子K均是Ⅰ型裂纹的应力强度因子KI。构件材料的KIc越高,其裂纹失稳扩展的速率越小,呈现反比关系。临界值KIc与KI相比较,可以判定裂纹是否发生失稳拓展。
查阅资料可知,应力强度因子的计算公式为
(1)
式中,a表示裂纹长度的二分之一,mm;σ表示均匀拉伸应力,MPa,K是裂纹的应力强度因子。
但是,如果构件的尺寸和裂纹的尺寸不是很小的情况下,必须要考虑构件的自由边界对裂纹尖端应力强度因子的影响,需要对公式(1)修正,修正后的公式为
(2)
其中,f为形状修正因子,用a的函数或者一个常数来表示,由裂纹加载方式、裂纹位置以及裂纹的形态决定。
3.2 疲劳裂纹扩展速度的确定
疲劳裂纹扩展速率可由Paris公式计算,其公式为
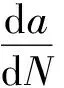
(3)
式中,da/dN表示疲劳裂纹的拓展速度,即构件在疲劳载荷的持续影响下,裂纹长度a随着循环次数N的变化率;ΔK为应力强度因子的幅度;C、m是材料参数,该参数是通过疲劳裂纹拓展速率实验,利用Pairs公式拟合实验数据而得到。
3.3 疲劳拓展寿命的预测
估算疲劳裂纹扩展寿命时,要先确定临界裂纹尺寸ac。
(4)
疲劳拓展寿命计算公式
(5)
其中,Nc为循环次数;Δσ为应力幅值;a0和ac分别为初始、临界裂纹长度。
根据本文有限元分析结果,取Δσ=30 MPa,Δσmax=130 MPa。
根据相关手册和工程经验取参数:f=1.12,kc=184.5 kJ/m2,a0=1 mm,c=3.25e-12,m=4。
代入式(4),得ac=0.51 mm
代入式(5),得Nc=24 436 997次
疲劳寿命分为裂纹初始寿命和裂纹扩展寿命两部分。两部分寿命在总寿命中所占有得比例,与构件的材料和结构特点紧密相关。通常来说,对于在产品加工的过程中不可避免将出现类裂纹缺陷或者裂纹,如铸件、焊等构件的裂纹扩展寿命就是其疲劳寿命。反之,对于那些一出现裂纹就有断裂危险、韧性较低的构件,其裂纹初始寿命就是其疲劳寿命。本文分析的门式起重机属于前者,因此该裂纹扩展寿命Nc=24 436 997次就是门式起重机的疲劳寿命。与有限元分析的最小寿命属于一个数量级,证实了采用有限元与断裂力学的方法计算门式起重机的疲劳寿命结果基本一致。
4 结论
(1)过有限元模型对两个典型位置进行静力学分析,得出起重机应力最大位置及变形最大位置位于主梁中间位置,验证门式起重机强度和刚度满足要求。
(2)建立疲劳分析框图,把有限元静应力分析结果导入nCode Design-Life软件,进行载荷映射和材料映射,获取门式起重机的安全使用寿命。
(3)多种工况的疲劳寿命分析结果对比,验证其疲劳寿命满足工程安全使用要求。
(4)基于断裂力学理论,计算起重机的裂纹拓展寿命,验证有限元分析结果的准确性。

