基于跟踪微分器的PMSM死区补偿策略
李有光,谭秀菲
(南京航空航天大学,南京 210016)
0 引 言
永磁同步电机(以下简称PMSM)具有结构简单、效率高、转矩电流比大、转矩脉动小等优点,在多个行业中得到了广泛应用[1-4]。在直流供电的PMSM驱动控制系统中,直接驱动PMSM的是三相逆变器,其同一桥臂上的开关管导通与截止均需要一定的时间。为防止上下管同时导通,进而出现电源短路的情况,上下管的导通信号之间必须存在一定的时间延迟,这段延迟时间即为死区时间。死区时间的存在,导致逆变器实际输出电压与目标电压并不相等,进而使得PMSM谐波含量增加、损耗加大,而且在低负载情况下会引起较大的脉动,甚至出现系统剧烈振荡,导致PMSM不能正常运行的情况发生[5]。
文献[6]中分析了矢量控制下PMSM在低速轻载时死区效应的影响,并利用d轴电流对表贴式PMSM不会产生磁阻转矩的特点,提出一种通过加大d轴电流来削弱零电流钳位效应进而对死区进行补偿的方法,但此方法只适用于表贴式PMSM。文献[7]利用电流的变化量建立与死区扰动电压之间的关系,以此来对死区进行补偿。该方法无需进行相电流极性判断,但更高的电流采样率增加了硬件成本及算力资源。文献[8]与文献[9]分别利用卡尔曼滤波器及拓展卡尔曼滤波器来实现死区补偿,此种方法计算量较大。文献[10]利用模糊控制器来动态调整死区补偿电压,进而实现死区补偿,但该方法的计算过程较为复杂。本文根据死区效应原理及特点结合上述方法的优缺点,提出了一种过程简单、计算量小、补偿效果优良的死区补偿策略。
首先,本文介绍三相逆变器的工作原理,并对死区效应进行详细分析。其次,采用低通滤波器对电流进行滤波,削弱零电流钳位现象的影响。然后,针对低通滤波器存在相位延迟问题,利用微分信号对其进行相位补偿。接着,将低通滤波器与微分器用跟踪微分器(以下简称TD)替代,简化过程。最后,根据仿真和实验来验证该方法的有效性。
1 三相逆变器的死区效应
本文采用下边沿三采样电阻电流检测的两电平三相逆变器结构,如图1所示。

图1 三采样电阻三相逆变器电路
以A相为例,定义电流流入电机为正,流出电机为负,开关管的状态及输出电压的变化如图2所示。

图2 A相开关状态及电压的变化
图2中,SAH_ideal、SAL_ideal分别为A相桥臂开关管S1、S2理想的导通与关闭过程,SAH_real、SAL_real分别为S1、S2实际的导通与关闭过程;UAN_ideal为A相理想电压输出,UAN_real为A相电流的实际电压输出(分ia>0与ia<0两种情况);Ton、Toff分别为开关管导通和关闭所需时间,Td为设定的死区延时时间;Vdc、Von、VRs、Vd分别为电源电压、开关管导通压降、采样电阻压降、续流二极管压降。其中,开关管导通压降Von、采样电阻压降VRs与电流幅值相关,可以将其等效为线性模型:
(1)
式中:Rson、RRs分别为开关管导通电阻、电流采样电阻。
当相电流ia>0时,上管导通,电流由电源正极经上管流入电机,由于上管存在导通压降,电机实际电压比正电压小Von。续流二极管工作时,电流由电源负极经采样电阻和二极管流入电机,电机实际电压比负电压小(VRs+Vd)。下管导通时,电流由电源负极经采样电阻和下管流入电机,电机实际电压比负电压小(VRs+Von)。
同理可得,当相电流ia<0时,电机实际电压比正电压大Von;续流二极管工作时,电机实际电压比正电压大Vd;下管导通时,电机实际电压比负电压大(VRs+Von)。
当ia>0时,A相平均电压的实际值与目标值的差值,即需要补偿的电压值,其数学表达式:

Toff(Vdc-Von)+
(Td+Ton-Toff)(VRs+Vd)+
[(1-D)Ts-Td-Ton](VRs+Von)+
Toff(Vdc+VRs+Von)+
(Td+Ton-Toff)(Vdc+Vd+VRs)]
(2)
式中:Ts为SVPWM载波周期;D为设定的占空比。
若令续流二极管工作时间:
τ=Td+Ton-Toff
(3)
式(2)可化简:
ΔUa=Von+(1-D)VRs+
(4)
同理可得,当ia<0时,A相平均电压的实际值与目标值的差值:
ΔUa=-Von-(1-D)VRs-
(5)
B、C相在一个SVPWM周期内的死区补偿电压计算方法与A相相同。
由于SVPWM载波频率远高于PMSM电磁时间常数,所以在一个控制周期内可以认为相电流绝对值、开关管导通内阻及采样电阻阻值为常数。在此条件下由式 (1)可知,该周期内Vdc、Von、VRs、Vd为常数。
由式(4)、 式(5)可知,在不采用电压补偿策略的情况下,可以利用多种方法来减小死区电压影响,如减小电源电压、增大SVPWM周期、采用更小导通内阻的开关管、采用更小阻值的采样电阻、采用更小导通压降的续流二极管。
虽然上述方法能够降低死区效应的影响,但同样会产生一定的不良影响。电源电压的减小会降低系统的调速范围,加大SVPWM周期会加剧PMSM抖振、降低系统稳定性,减小采样电阻会导致电流测量噪声加大,采用导通内阻更小的开关管和更小导通压降续流二极管会导致成本上升。与此相比,采用死区补偿的方法更加高效便捷,并且能在理论上消除死区效应影响。
2 死区补偿策略
2.1 静止坐标系下的死区电压
由于SVPWM调制需要将目标电压变换到两相静止坐标系下,因此将补偿电压转换到两相静止坐标系下:
式中,ΔUα、ΔUβ为两相静止坐标系下的补偿电压;iα、iβ为两相静止坐标系下的电流。设目标电压为Uα_aim、Uβ_aim,则经过补偿后的电压:
(7)
2.2 TD
由前文分析可知,补偿电压与相电流极性有关,但由于存在测量噪声、零电流钳位效应,相电流极性判断容易出错,故需要对相电流进行滤波处理,去除高频噪声的影响。常见低通滤波器虽然结构简单,计算量小,但其相位延迟随着系统频率升高而变大,在PMSM高速运行时影响较大。卡尔曼滤波器等高级滤波器虽然滤波效果较好,但该算法的过程较为复杂、运算量大,对控制器性能要求高。
本文采用包含相位补偿措施的低通滤波器进行滤波,该方法不仅具有较好的滤波效果,而且其运算量不大。相位补偿公式如下:
y=u+λhv
(8)
式中:y为补偿后的信号;u为滤波后的信号;v为信号的微分;h为采样步长;λ为补偿系数。由式 (8)可知,补偿过程需要信号的微分,传统获取信号微分的方式是通过经典微分器获得,其原理是用惯性环节跟踪原始信号信号,即:
(9)
式中:u(s)为输入信号;G(s)为微分器传递函数;v(s)为所得信号的微分;τ为时间常数。当τ足够小时,G(s)≈s,即等效为微分环节;当s→∞时,|G(s)|=1/τ,即其高频增益会随着τ减小而增大,从而使得高频噪声的影响被放大。韩京清[11]改用振荡环节取代原本的惯性环节,即:
(10)
由上式可知,G(s)是一个阻尼比为1的二阶滤波器,它的特征方程有两个负重根s1、2=-r。r的大小决定了其动态部分的衰减速度,被称为速度因子。当τ足够小时,G(s)≈s,等效为微分环节;当s较大时,G(s)≈r2/s,其高频增益随着s增大而减小,这就使其对高频噪声有着显著的抑制作用,能更好地跟踪微分信号。
上述微分器都是通过跟踪原始信号的微分而近似达到获得微分的效果,被称为TD。
针对离散系统,将G(s)离散化:
(11)
式中:x1为跟踪输入信号;x2为跟踪输入信号的微分。韩京清[11]用基于离散系统的非线性最速控制综合函数fhan(x1,x2,r,h)对上述微分器结构做了改进,使其能快速跟上微分信号且不存在由于离散化而产生的高频抖振[11-15]。改进后的跟踪微分器被称为最速离散跟踪微分器,其离散方程:
(12)
式中:u为输入信号;x1跟踪输入信号;x2跟踪输入信号的微分;r对应式(10)中的速度因子;h为采样步长。离散最速控制函数fhan(x1,x2,r,h)表达式如下:
(13)
式中:r为速度因子;h积分步长,与式 (12)相同。
由TD的相频特性可知,通过调节速度因子r可得到对应频率的低通滤波器[11],其截止频率:
(14)
2.3 基于TD的滤波器设计
由前面分析可知,整个滤波系统由一个低通滤波器和一个TD构成。由式(11)、式(12)可知,TD对原信号的跟踪与低通滤波器的作用相同,因此可以省略低通滤波器,只用TD配合适当的参数,即可达到相同的目的。基于TD的相位补偿如图3所示。
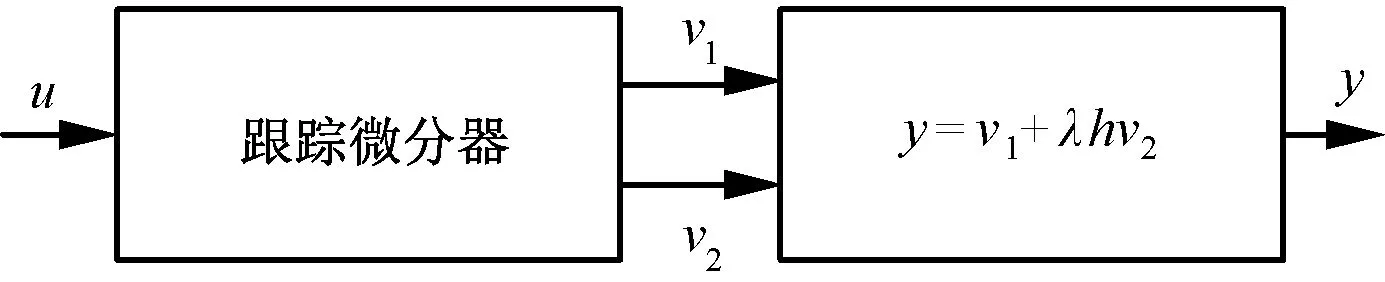
图3 基于TD的相位补偿示意图
图3中,u为输入信号,v1、v2为跟踪微分器对信号及信号微分的跟踪,λ为相位补偿的步数,y为最终信号。
在滤波器参数设置时,截止频率设置太高会使得低转速下滤波效果太差,设置太低会使得高转速下波形失真严重。而PMSM的电流信号频率与电角速度相关,而电角速度与转子转速相关,又因为转子转速可以通过编码器间接得到,因此可以设置截止频率:
(15)
式中:Kc为比例系数;ωr为转子角速度;ωmin为最小频率阈值。
在PMSM实际控制系统中,电流的采样始终落后于实际值一个周期。换而言之,在第k个时期计算第k+1时期的控制量时,所用的电流值是第k-1周期作用后的电流值,而不是理想中k周期作用后的。具体过程如图4所示。

图4 电流采样的延迟
综上,可得加入相位补偿后的滤波器参数:
(16)
由于PMSM的相电流是正弦信号,故相位延迟影响较为明显;而d,q轴电流在电机稳定运行时为定值,此时相位延迟的影响可以忽略。因此,可以应用滤波器对d,q轴电流进行滤波,再反变换到三相静止坐标系下,减小相位延迟的影响。由于在负载变化时d,q轴电流会跟随变化,此时相位延迟会影响判断结果,若波动持续时间较长则可能引起补偿失败,因此相位补偿不可省略。
3 仿真及实验验证
3.1 仿真验证
基于TD的死区补偿策略系统框图如图5所示。

图5 PMSM矢量控制系统框图
在Simulink仿真环境里按图5搭建仿真模型,PMSM电机参数如表1所示,逆变器参数如表2所示。

表1 PMSM参数

表2 逆变器参数
初始负载转矩0.05 N·m,转速500 r/min。稳定后引入0.1 N·m的负载波动,电流反馈加入高斯白噪声。滤波器速度因子Kc=1 000,h=0.000 05,相位补偿步数λ=2。仿真结果如图6~图9所示。
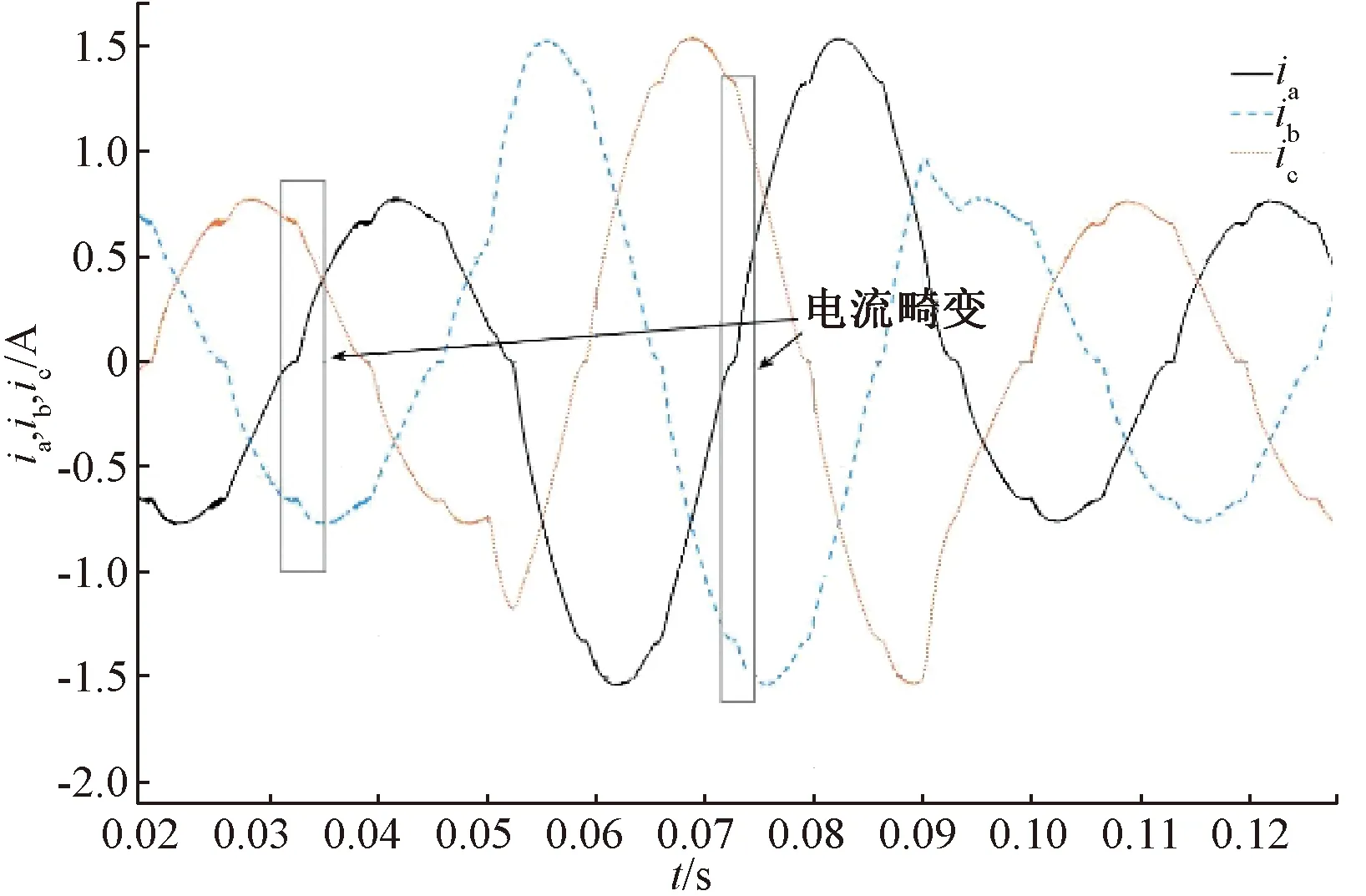
图6 PMSM的死区效应
由图6可以看出,加入死区后的PMSM电流有明显的零电流钳位现象出现,即某一相电流过零位时会出现一个“平台”,并且对其余两相也造成影响,进而导致相电流在一个周期内出现6个“平台畸变”。由图7可以看出,加入噪声后的电流在过零位时会出现反复跳动,同时电流的畸变效应不明显,因此不能直接应用此电流做死区补偿,必须进行滤波处理。由图8可以看出,在负载波动开始后的一个周期内仍存在电流畸变,而在负载稳定时电流无畸变。这就说明,若只对d,q轴电流进行滤波处理而不进行相位补偿,则会在负载波动(d,q轴电流跳变)时由于相位滞后而导致补偿失败。由图9可知,经过相位补偿后,即使在负载波动情况下基于TD的死区补偿策略也可以补偿成功。
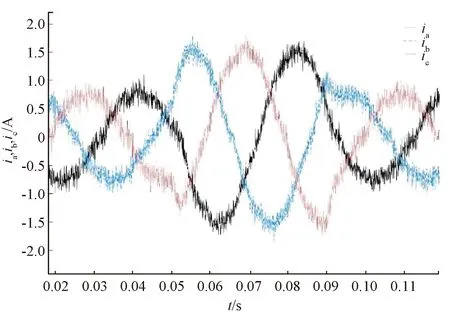
图7 加入噪声后的电流
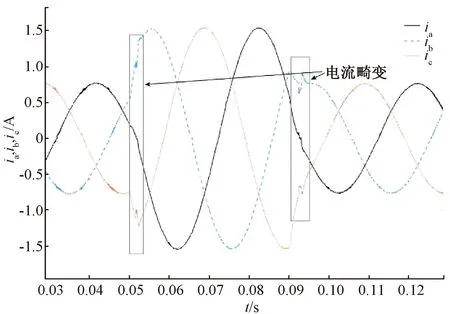
图8 未加相位补偿的死区补偿后电流

图9 带相位补偿的死区补偿后的电流
通过仿真结果对比可知,基于TD的死区补偿策略不仅对电流信号有着较好的滤波作用,还不会因为相位延迟而导致补偿失败,进而使得死区补偿后电流失真程度大幅减小,验证了基于TD的死区补偿策略的可行性。
3.2 实验结果
本文采用的实验平台如图10所示,实验装置主要有直流电源、永磁同步电机、控制器、上位机等。电机参数及逆变器参数与仿真环境设定的参数保持一致,位置传感器采用14位增量式编码器,控制器采用单片机STM32H750,利用单片机ADC模块对电流进行采样。为方便观察死区效应及死区补偿效果,实验电机在轻负载条件下运行,即电机只连接行星减速器,不另加负载。电机稳定运行后对其施加小负载波动,得到对应的电流响应。电流值、转速值等数据经单片机采集,然后发送至电脑由origin软件做可视化处理,以此查看电流波形变化。

图10 实验平台
电机在不进行死区补偿以及进行死区补偿后的相电流波形(滤除噪声后)如图11、图12所示。

图11 未进行死区补偿的相电流
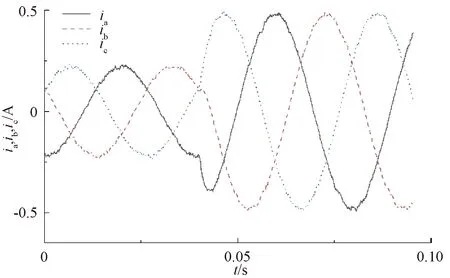
图12 加入死区补偿后的相电流
由图11、图12可知,未进行死区补偿时,电流波形出现明显的畸变,有零电流钳位现象和波峰畸变,补偿后电流波形基本消除了畸变,波形接近正弦波。
4 结 语
针对三相逆变器死区效应引起的PMSM电流畸变,本文采用基于TD的死区补偿策略进行补偿。该策略利用TD构建带有相位补偿功能的电流滤波器,在电流存在噪声的情况下仍能对死区进行有效补偿,提高了系统的稳定性。此外,该方法还具有运算过程简单、工程实用性强、占用控制器资源少等优点,仿真及实验结果验证了此方法的可行性与有效性。

