基于响应面法的圆筒型永磁直线电机推力特性优化
付 豪,吴尧辉
(河南理工大学 电气工程及其自动化学院,焦作 45400)
0 引 言
圆筒型永磁直线电机(以下简称TPMLM)具有推力密度大、动态响应快、运行可靠、无横向边端效应等优点[1-3],在油田抽油机[4]、精密机床等[5]高动态响应伺服场合以及直线驱动领域得到了广泛的应用。
然而,TPMLM定子铁心两端开断和定子开槽,其存在端部效应[6]和齿槽效应[7]。由齿槽效应引起的齿槽力和端部效应引起的端部力,导致TPMLM存在较大的推力波动,严重影响了电机运行性能,也限制了其应用范围。因此,减小电机的推力波动,提高平均推力,以获得良好的推力特性至关重要。
针对此问题,国内外学者在电机本体结构上做了大量的研究。文献[8]提出了一种初级斜端部结构,有限元仿真结果表明,其可以有效减小TPMLM的端部力,从而降低推力波动;文献[9]通过采用不等宽槽口,来减小TPMLM的齿槽力,样机实验证明该方法可以有效地降低推力波动;文献[10]通过在初级齿部加附加槽来减小TPMLM的推力波动,并对附加槽的形状和最佳尺寸进行了研究;文献[11]提出一种采用定子和动子不等极距的方法来减小TPMLM的齿槽力;文献[12]采用辅助槽来减小TPMLM的齿槽力,并研究了辅助槽尺寸对TPMLM齿槽力的影响;文献[13]提出优化电机的极弧系数来减小永磁直线电机的齿槽力;文献[14]提出一种磁极分组偏移的方法来减小电机齿槽力。永磁电机各参数之间的耦合性是极强的,虽然这些方法可以有效地降低推力波动,但也可能降低电机的推力,影响电机的推力特性。
本文基于有限元分析,以TPMLM的平均推力和推力波动为优化目标,优化电机结构参数设计。首先,采用田口法分析电机结构参数的敏感性,从8个结构参数中选出4个敏感参数;然后,构建基于Box-Behnken法的响应面模型,采用NSGA-II多目标遗传优化算法对该响应面模型进行求解;最后进行了有限元仿真验证。
1 电机结构及参数
本文以9槽10极TPMLM为研究对象,图1为圆柱坐标系下电机的模型,图2给出了TPMLM的8个结构参数,包括定子齿部高度h0和h1,定子齿部宽度w2,槽部高度h2,槽部宽度w3,气隙宽度w4,磁极宽度w1,磁极高度h3。TPMLM的结构参数如表1所示。

图1 TPMLM模型
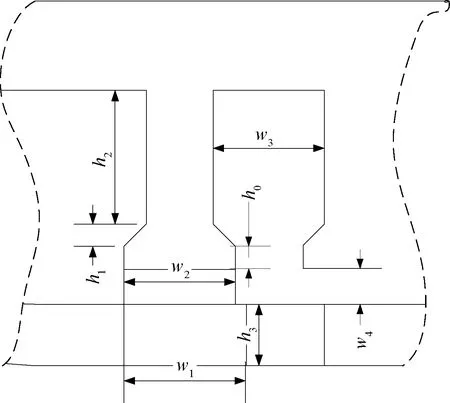
图2 TPMLM结构参数
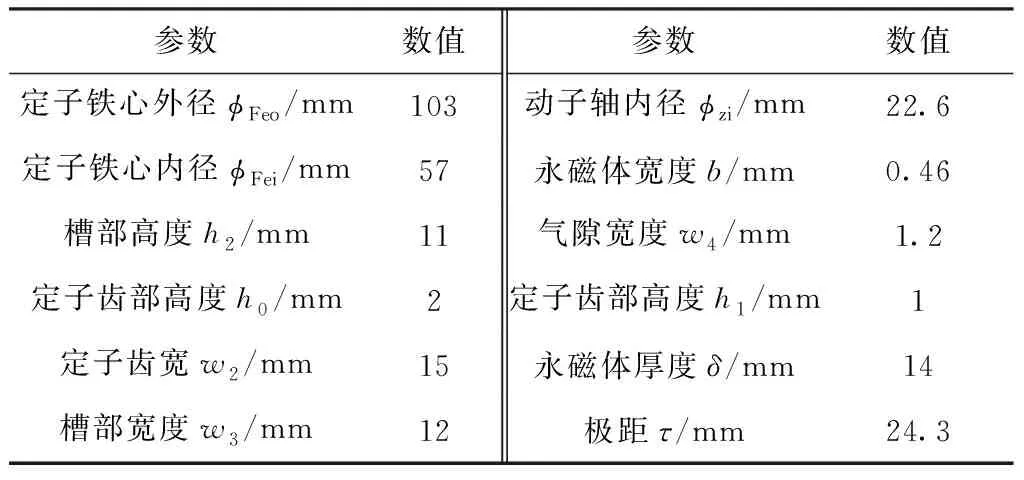
表1 TPMLM结构参数
2 参数敏感性分析
为了降低优化问题维度,提高优化效率,从这8个结构参数中选出对TPMLM推力和推力波动有显著影响的参数。首先,将8个结构参数分为两组:第一组是关于定子齿部的结构参数h0,h1,w2;第二组是其它的5个结构参数h2,h3,w1,w3,w4。然后,采用田口法,分别对这两组参数建立正交实验矩阵,通过方差分析和信噪比分析,选出对TPMLM推力和推力波动有显著影响的参数。
2.1 第一组结构参数敏感性分析
首先,对定子齿部的3个结构参数进行实验设计,如表2所示。接着,利用有限元软件Magnet计算出每次实验的目标值,填入表2中,对表2进行方差分析和信噪比分析。图3为推力波动的信噪比,图4为平均推力的信噪比,方差分析结果如表3所示。
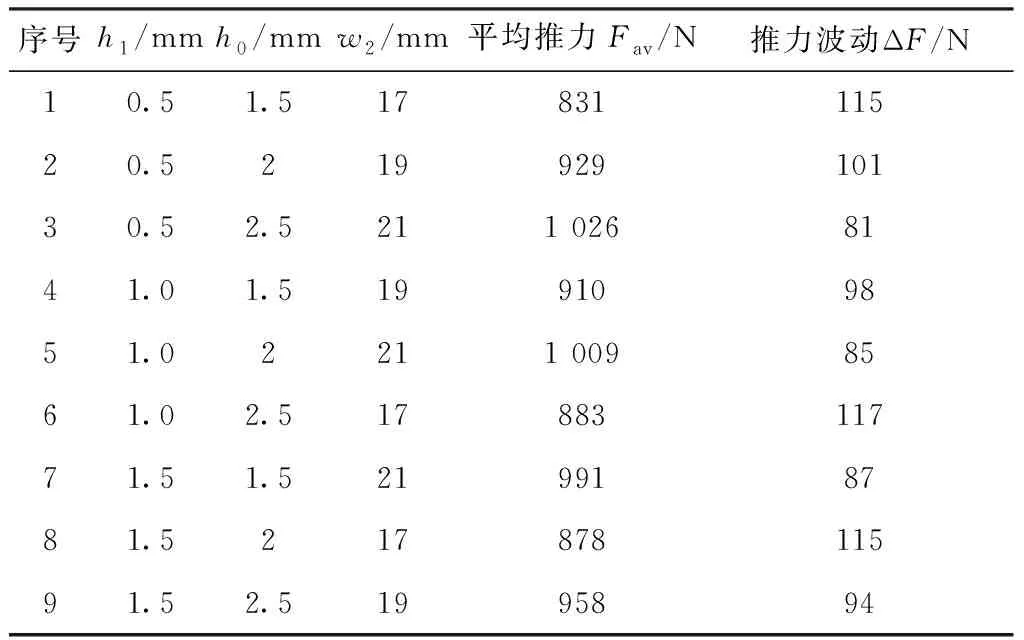
表2 第一组结构参数正交表及分析结果
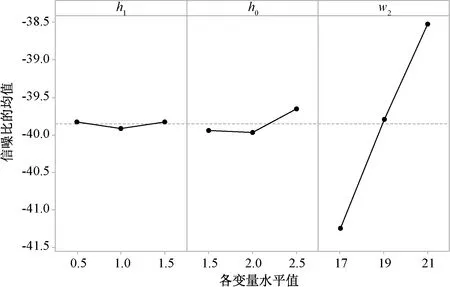
图3 第一组参数推力波动的信噪比
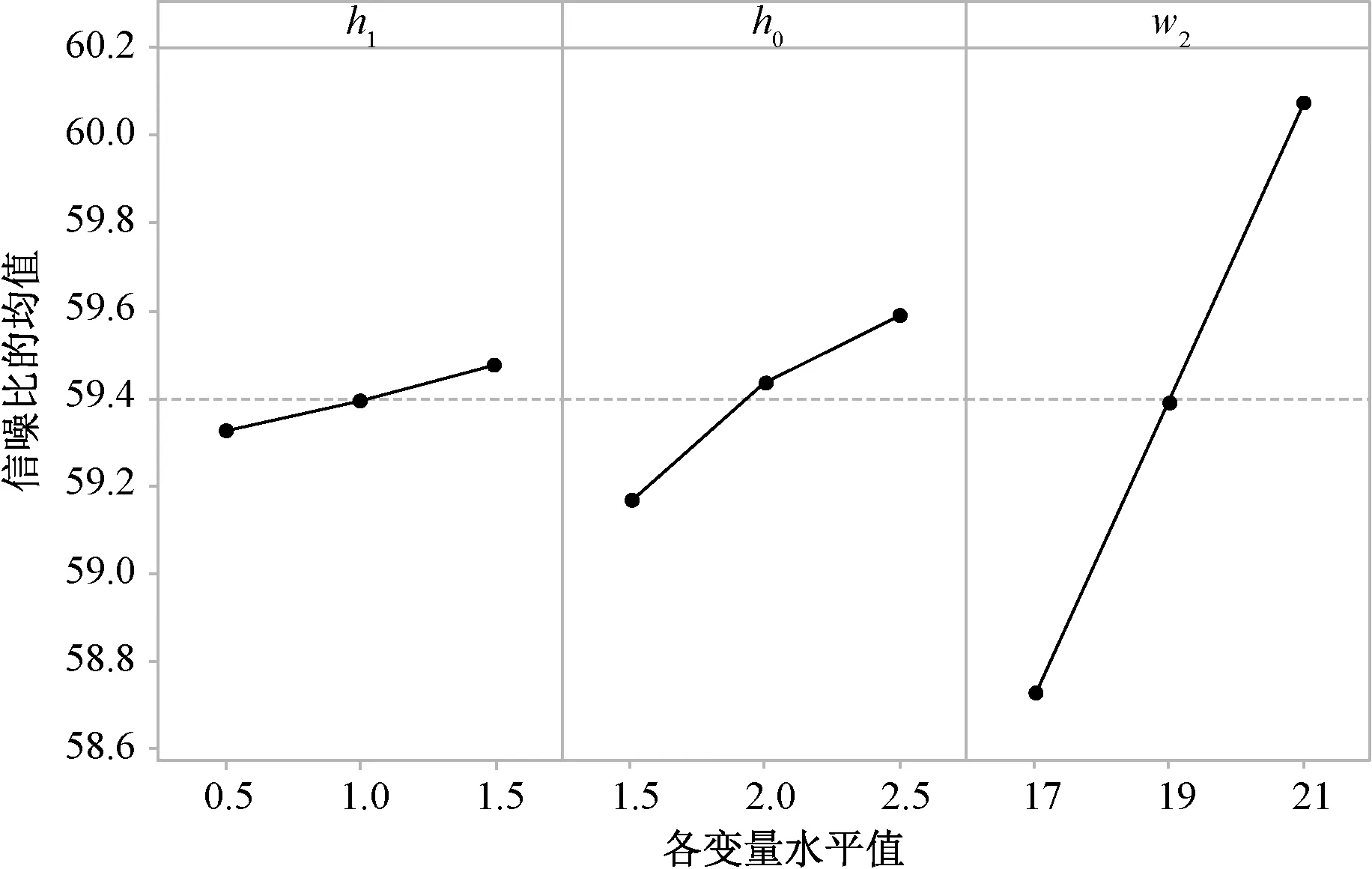
图4 第一组参数平均推力的信噪比

表3 第一组参数方差分析
由图3、图4和表3可看出,定子齿部结构参数w2对推力波动和平均推力都有显著影响,而h0和h1对推力波动和平均推力影响比重都小,因此将w2确定为优化变量。根据图3和图4的信噪比分析结果,取h0=2.5 mm,h1=1.5 mm。
2.2 第二组结构参数敏感性分析
同样,建立一张关于h2,h3,w1,w3,w45个结构参数的L1645正交表,表4为这5个参数的正交表和有限元分析结果,图5和图6分别为第二组参数推力波动和平均推力的信噪比分析结果,表5为方差分析结果。
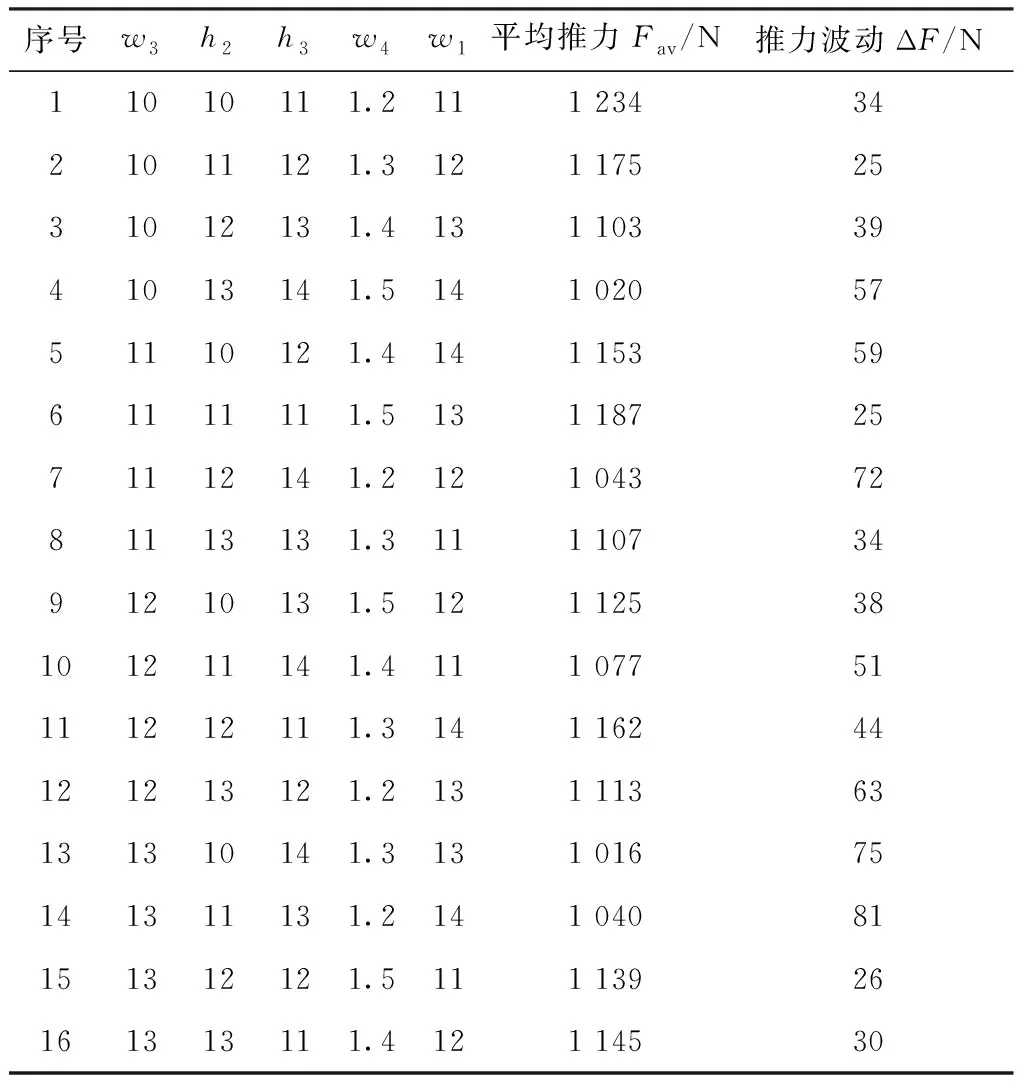
表4 第二组结构参数正交表及分析结果

图5 第二组参数推力波动信噪比
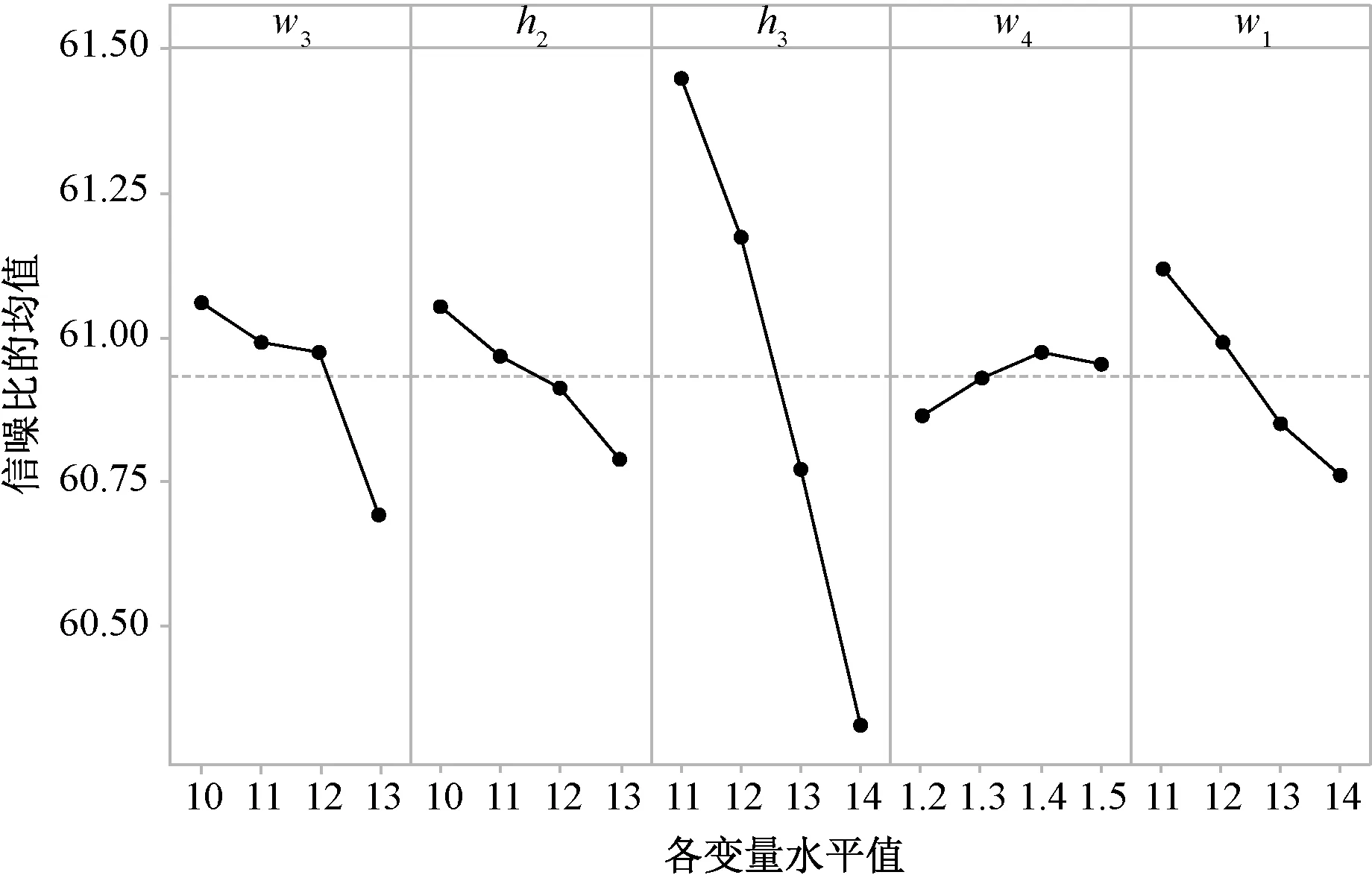
图6 第二组参数平均推力信噪比

表5 第二组参数方差分析
由图4、图5和表3可以看出,h3对平均推力有显著影响,而h3、w1和w4对推力波动有显著影响,因此将h3、w1和w4确定为优化变量。根据图4和图5的信噪比分析结果,取h2=11 mm,w3=10 mm。
综上,根据对两组参数的敏感性分析结果,确定h3、w1、w2、和w4共4个结构参数为优化变量。
3 构建响应面模型
响应面模型是一种数学建模优化和综合实验设计方法,可以有效减少实验次数,准确分析设计变量之间的相互作用。Box-Behnken法是响应曲面设计中常用的一种设计方法。采用Box-Behnken法进行实验设计时,每个因子取3个水平的值,分别为设计变量优化区间的中心值、上限和下限值。表6为各个优化变量的水平值。

表6 设计变量水平值
根据Box-Behnken法的实验设计原则,建立一个关于4个变量的正交实验矩阵,共需要进行27次实验。通过有限元分析,计算出每次实验的平均推力和推力波动。正交实验矩阵和优化目标的实验结果如表7所示。

表7 正交实验矩阵及实验结果
根据表7的正交实验矩阵和有限元分析得到的结果,对优化目标进行表面响应分析。通用的二阶响应面模型如下式[15]:
(1)
式中:G(t)为响应值;a0、ai、aj为回归系数;ti、tj为两个不同的优化变量;ε为拟合误差。
对表7中的数据进行多元二次回归拟合,即可得到响应面的数学模型。TPMLM平均推力的拟合回归方程:
f1=400+12.42w2+132.1h3-699w4+
41.9h3w4-6.56h3w1+76.9w4w1
(2)
TPMLM推力波动的拟合回归方程:
f2=-750+52.5w2+30.5h3+64w4+
3.37w2h3+16.2w2w4-3.25w2w1-
19.37h3w4+2.125h3w1-15w4w1
(3)
4 多目标算法寻优
TPMLM各个结构参数之间存在相互作用,会使得优化目标不能同时达到最优。采用多目标遗传优化算法,以最大的平均推力、最小推力波动为目标进行多目标优化求解,数学模型可以表示:
(4)
式中:f1(x)为电机的平均推力函数;f2(x)为电机的推力波动函数;f3(x)为一个磁极用磁量的函数;xil和xih分别为第i个变量的最小值和最大值;w1、w2、w4和h3参数的取值范围:
通过多目标遗传优化算法求解,获得Pareto前沿,如图7所示。
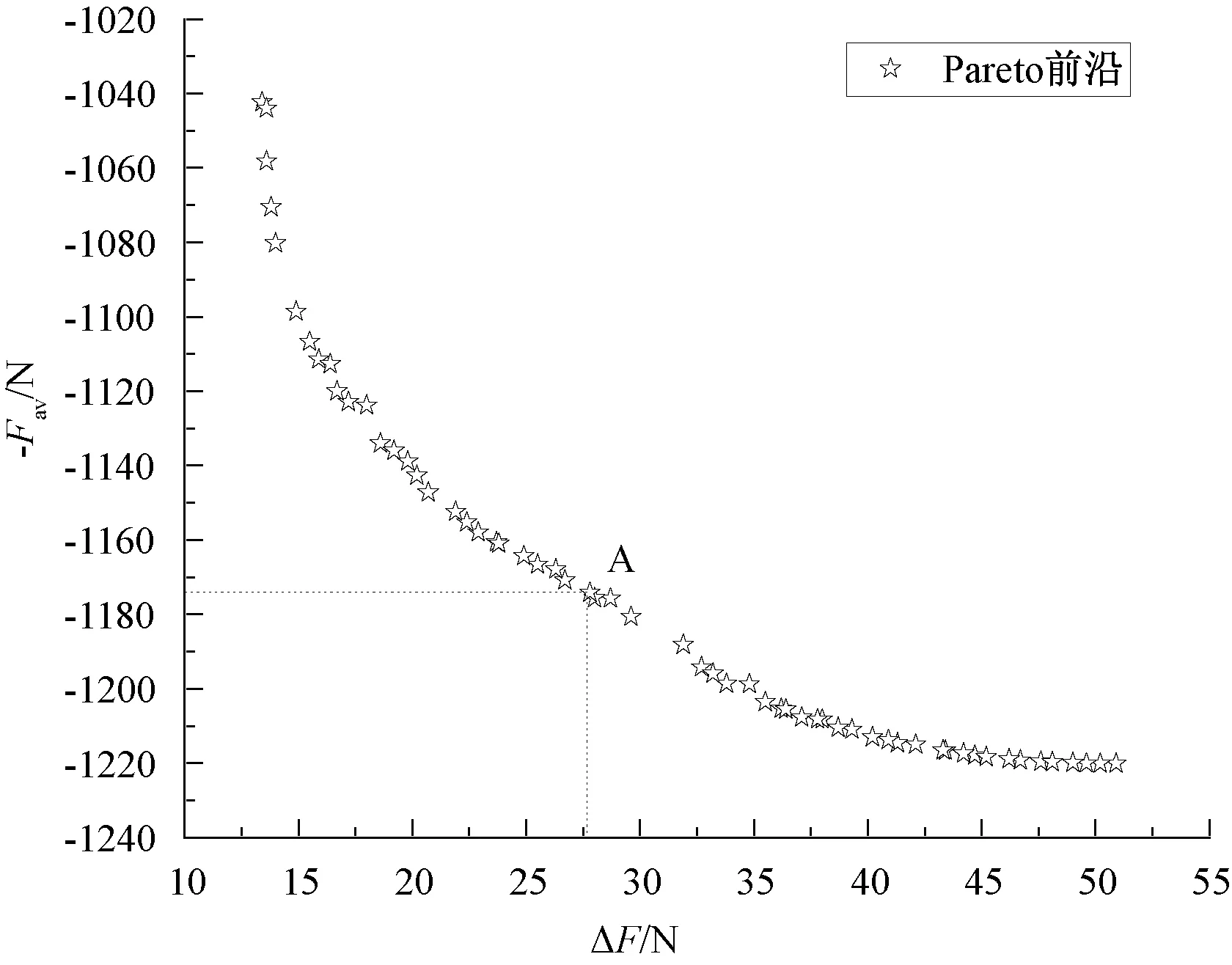
图7 Pareto前沿图
从Pareto解集中选择一组解A为TPMLM最优参数组合,如表8所示。

表8 最优参数组合
5 电机优化前后性能对比
利用有限元软件Magnet对表8参数组合的TPMLM电磁模型进行有限元分析。图8为优化前后TPMLM稳定运行后电机的推力波形,表9为TPMLM的优化结果。
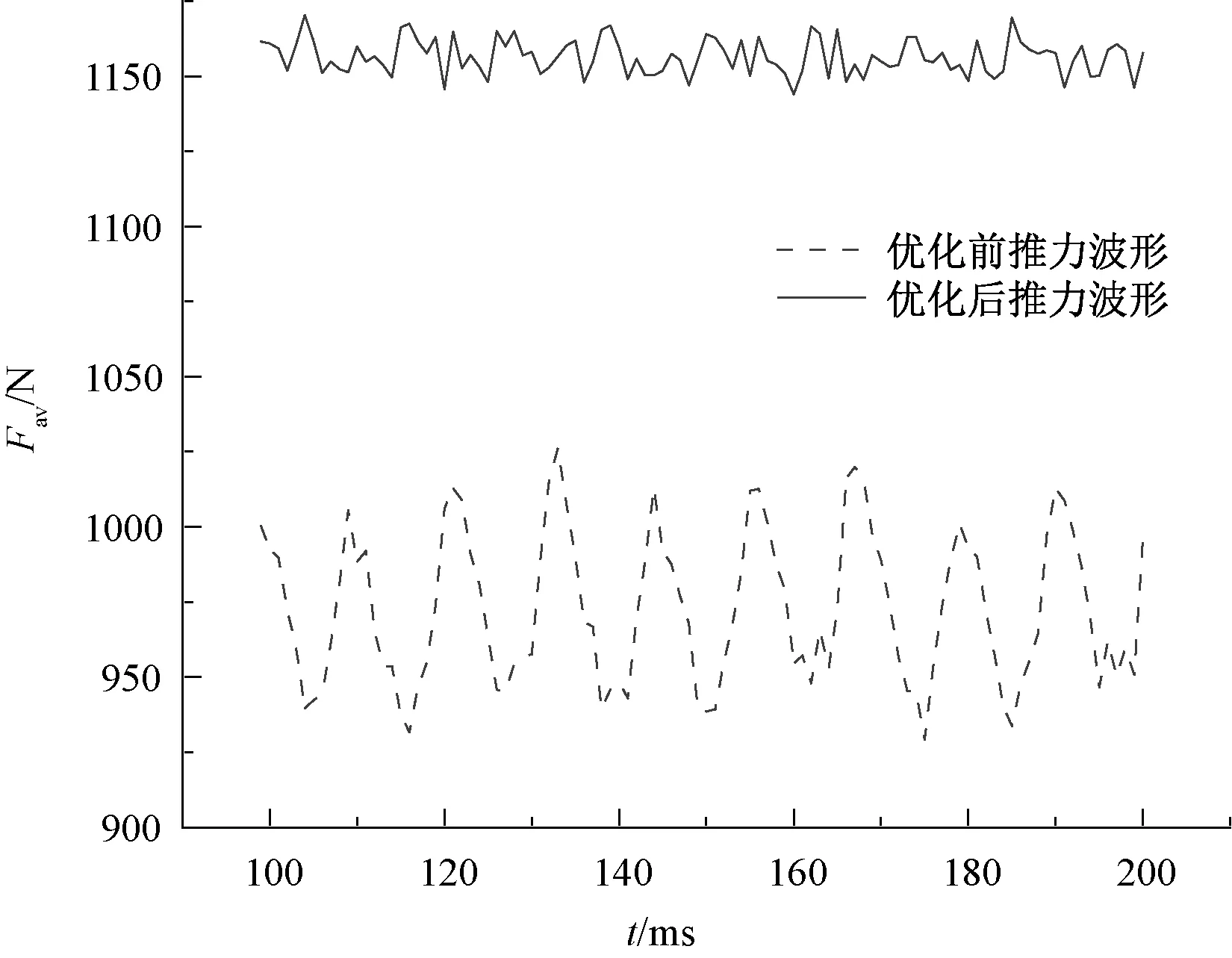
图8 优化前后推力波形

表9 优化前后TPMLM性能对比
从图8中可以看出,优化前电机的平均推力约为975 N,推力波动约为97 N;优化后电机的平均推力约为1 157 N,推力波动约为26 N。优化后电机的平均推力提高了18.67%,推力波动降低了73.20%,经过优化后,电机用磁量减小了22.67%。显然,表8中的参数组合可以提高TPMLM的推力,降低推力波动。
6 结 语
本文对9槽10极TPMLM进行了优化设计,以推力和推力波动为优化目标,选取TPMLM的8个结构参数为优化变量。基于田口法的参数敏感性分析显示,定子齿部宽度和磁极厚度对电机推力有显著影响,定子齿部宽度、气隙宽度、磁极宽度和磁极厚度对推力波动有显著影响。结合响应面法建立TPMLM平均推力和推力波动关于定子齿部宽度、气隙宽度、磁极宽度和磁极厚度的二阶响应面模型,采用多目标遗传优化算法对该响应面模型进行求解,获得最优参数组合。有限元仿真结果表明,与原始电机相比,优化后TPMLM的平均推力提高了18.67%,推力波动降低了73.20%,用磁量减小了22.67%,说明求得的最优参数组合可以有效提升TPMLM的推力特性,也说明了优化方法的可行性与有效性。

