如何正确运用方差分析
——单因素多水平设计定量资料一元方差分析
胡纯严,胡良平,2*
(1.军事科学院研究生院,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029
单因素多水平设计是生物医学试验研究中使用频率极高的一种设计类型。当观测结果变量为定量变量时,常选用的统计分析方法被简称为“单因素方差分析”。本文着重介绍该设计定量资料一元方差分析的前提条件、基本思想、计算公式和基于SAS软件的实例分析。
1 单因素多水平设计定量资料一元方差分析
1.1 前提条件
第一个前提条件为“独立性”,即全部定量数据中的任何两个数据之间必须相互独立[1];第二个前提条件为“正态性”,即某因素各水平组定量数据必须抽自正态分布的总体(需要分组进行正态性检验)[2];第三个前提条件为“方差齐性”,即某因素k个水平组定量数据应抽自方差相等的k个总体(需要对定量资料中每个因素所有水平组的总体方差进行方差齐性检验)[3]。
1.2 方差分析的基本思想与计算公式
单因素多水平设计定量资料一元方差分析的基本思想是关于总离均差平方和的分解,即将全部数据关于总均值的离差平方和分解成组间离均差平方和与组内(或称误差)离均差平方和两部分,自由度也有类似的分解方法。将各部分离均差平方和除以各自的自由度,就是各项的方差(或称均方)。以组内(或误差)均方为分母,以组间均方为分子,就可以构造出一个检验统计量F。
对于单因素多水平设计一元定量资料而言,其总离均差平方和SS总可按下式分解[4]:
式(1)中,三项离均差平方和的表达式如下:

基于离均差平方和与自由度构造均方MS,见式(6)、式(7):

基于均方构造检验统计量F,见式(8):

在式(8)中,F服从分子自由度为df组间、分母自由度为df误差的F分布。
若采用手工计算,需要通过查F界值表(单侧检验),可得F(1-α)(df组间,df误差),若F≥F(1-α)(df组间,df误差),则P≤α,反之,则P>α。最后,确定P值并作出统计推断,再结合专业知识给出专业结论。
2 实例与SAS实现
2.1 问题与数据结构
【例1】根据胆囊纤维化患者胰腺功能(胰蛋白酶分泌量),研究者将患者分为A、B、C三组:A组胰蛋白酶分泌量≤50 U/kg·h-1;B组胰蛋白酶分泌量为51~1000 U/kg·h-1;C组胰蛋白酶分泌量>1000 U/kg·h-1。三组的样本含量分别为9、10、9例,测得每位受试对象的蛋白质浓度(mg/mL)如下。A组:1.7、2.0、2.0、2.2、4.0、4.0、5.0、6.7、7.8;B组:1.4、2.4、2.4、3.3、4.4、4.7、6.7、7.6、9.5、11.7;C组:2.9、3.8、4.4、4.7、5.0、5.6、7.4、9.4、10.3[5]。分析三组患者蛋白质浓度平均值之间的差异是否有统计学意义?
【例2】为研究钙离子对体重的影响,某研究者将36只肥胖模型大白鼠随机等分为三组,每组12只,分别给予常规剂量钙(0.5%)、中剂量钙(1.0%)和高剂量钙(1.5%)三种不同的高脂饲料,喂养9周,测量并计算其喂养前后体重的差值[2]。分析三种不同剂量钙作用下大白鼠体重改变量的均值是否相等?
2.2 对例1资料的分析与解答
【分析与解答】这是一个单因素三水平设计一元定量资料,设所需要的SAS程序如下:

【SAS程序说明】当各组样本含量不等时,以样本含量最多的组为基准,样本含量少的其他组缺少几个数据就用几个“点”填充。

【SAS输出结果及解释】
以上输出结果表明:三组患者蛋白质浓度的均值差异无统计学意义(因F=1.26,df=2,P=0.2998>0.05),故可以认为不同胰蛋白酶分泌量对蛋白质浓度的影响不明显。三组定量资料的箱图见图1。

图1 三组定量资料的箱图
图1中,从左到右共有3个长方形,每个长方形中的横线代表各组定量资料的中位数所在的位置;每个长方形中的小正方形代表各组定量资料的平均值所在的位置,各组具体的平均值和标准差如下:

2.3 对例2资料的分析与解答
【分析与解答】这是一个单因素三水平设计一元定量资料,设所需要的SAS程序如下:


【SAS程序说明】第2个“means语句”给出了三个选择项,分别代表三种多重比较的方法,在GLM过程中,类似的比较方法还有很多,此处从略。
【SAS输出结果及解释】

以上输出结果表明:三组大白鼠体重改变量的均值差异有统计学意义(因F=31.49,df=2,P<0.0001),故可以认为饲料中钙剂量不同,大白鼠体重增加量也不同。饲料中钙剂量越高,大白鼠体重增加量越少。饲料中钙剂量由低到高对应的三组大白鼠体重增加量的箱图见图2。

图2 饲料中钙剂量由低到高对应的三组大白鼠体重增加量的箱图
在图2中,从左到右有3个长方形,每个长方形中的横线代表各组定量资料的中位数所在的位置;每个长方形中的小正方形代表各组定量资料的平均值所在的位置,各组具体的平均值和标准差如下:
注:此检验控制Ⅰ型比较误差率,不是试验误差率。
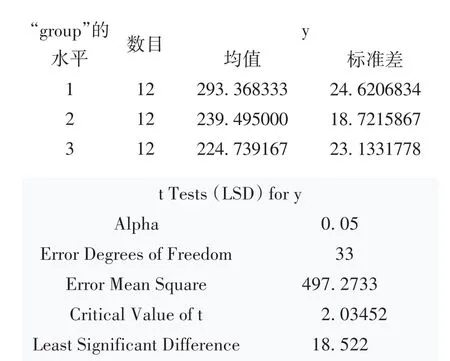
基于LSD法(即成组设计一元定量资料t检验)进行均值之间两两比较的结果见图3。

图3 基于LSD法进行均值之间两两比较的结果

注:此检验控制Ⅰ型试验误差率,对应的假设为完全无效假设,但不是部分无效假设。
基于SNK法进行均值之间两两比较的结果见图4。

图4 基于SNK法进行均值之间两两比较的结果
对输出结果的解释和结论同上(见图3后面的解释),此处从略。

注:此检验控制Ⅰ型试验误差率,但一般来说,此法比REGWQ法具有更高的Ⅱ型误差率。
基于TUKEY法进行均值之间两两比较的结果见图5。

图5 基于TUKEY法进行均值之间两两比较的结果
对输出结果的解释和结论同上(见图3后面的解释),此处从略。
3 讨论与小结
3.1 讨论
严格地说,用多次t检验取代方差分析的做法欠妥。事实上,当采用多次t检验进行n(n≥3)个均值两两比较时,可知比较的次数有c=n!/2!(n-2)!。比较的次数越多,在无效假设为真时,拒绝无效假设的Ⅰ类错误概率也越大。设每次检验水准即犯Ⅰ类错误概率为α,累积Ⅰ类错误的概率为α’,则对多个均值进行c次检验时,根据概率乘法原理,其累积Ⅰ类错误概率与c的关系见式(9)[6]:

例如,设α=0.05,c=3,其累积的Ⅰ类错误概率为:α’=1-(1-0.05)3=0.0143。可见,用多次t检验取代方差分析,意味着Ⅰ类错误概率会增大,即出现假阳性的可能性会增加。因此,不应该用t检验取代方差分析。
一般来说,对单因素多水平设计定量资料进行一元方差分析后,若结论是各水平组的均值差异有统计学意义,这是一个概括性的结论,它并不意味着任何两个平均值之间的差异都有统计学意义。欲知详情,应对多个均值进行多重比较。然而,对多个均值进行两两比较的方法很多,其区别是不同方法控制的误差类型不同。详见文献[7-8]。
进行方差分析前,需检查定量资料是否满足三个前提条件。因篇幅所限,本文在分析实例时,假定资料满足方差分析所需要的前提条件。在实际应用中,应严格检查给定资料是否满足前提条件。否则,方差分析的结果可能不准确。
3.2 小结
本文介绍了与单因素多水平设计定量资料一元方差分析有关的主要内容,包括前提条件、基本思想和计算公式。借助SAS软件对两个实例进行了方差分析,还采用三种两两比较的方法(即LSD法、SNK法和TUKEY法)对例2中的三个均值进行了分析。最后,在讨论中阐明了不适合采用多次t检验取代方差分析的理由。

