基于优化支持向量机的强夯有效加固深度研究

张鑫盛业谱邓祥文李书蓉李秀荣

(1.山东建筑大学土木工程学院，山东济南 250101；2.山东建筑大学建筑结构加固改造与地下空间工程教育部重点实验室，山东 济南 250101；3.山东建大工程鉴定加固研究院，山东 济南 250014)

0 引言

强夯法[1]是法国Menard公司在20世纪70年代创造的一种经济有效的地基处理方法。为了确保处理后地基场地工程可靠性，有必要对强夯作用过程进行深入研究，而强夯过程是高速瞬时冲击的动力学历程，整个过程作用机理复杂、影响因素繁多且具有高度的非线性，近半个世纪以来，工程界在其力学模型、能量响应的仿真模拟及理论解析课题上仍面临许多困难。

在围绕强夯法的研究中，有效加固深度的标定是应用强夯实现地基处理时的核心环节。强夯有效加固深度[2]是指经强夯处理后的地基土力学指标满足设计要求的深度范围，是关系到地基处理质量的一项决定性指标，有效加固深度的研究由最初强夯理论提出时的Menard公式系数修正法[3]，逐步发展出BILLAM经验计算法、刘海冲经验公式法等诸多基于试验与工程现场数据的计算方法。近年来，学者们从能量守恒[4]、量纲匹配[5]、相关性分析等方面对强夯的有效加固深度理论进行了更深层次的数值解析预测与分析[6]。强夯过程过于复杂且非线性程度很高，相关经验公式、力学模型等存在较大的局限性，同时诸多经验公式的简化与调参过程不可避免地产生误差，因而对于有效加固深度预测模型与算法研究仍是当前亟待解决的难题。

随着现代电子计算机的发展以及科学计算语言的进步，许多学者采用基于机器学习及智能算法预测了有效加固深度，如基于模糊信息优化处理技术[7]、BP人工神经网络技术(Back Propagation-Artificial Neural Networks，BP-ANN)[8]。其中，神经网络算法在预测领域得到了广泛的应用，但是由于其在局部极小值的处理以及学习训练过程中过分依赖经验或大量样本数据集等方面的缺陷，降低了该算法在强夯有效加固深度问题上应用的准确性与有效性。在工程数值问题的回归分析中，许多学者应用支持向量机算法的研究取得了进展，改进支持向量机算法在机械系统故障自动化诊断[9]、隧道结构行为分析[10]、航空航天器服役状态评估[11]等研究课题中得到重视和发展。

文章提出了应用异于传统机器学习方法的支持向量机算法模型回归预测强夯有效加固深度，是支持向量机算法在该工程问题上的初步尝试。通过编程构建(Support Vector Machines，SVM)模型，并设计遗传算法程序模块优化模型中的关键参数，实现了对数据的最优分析与预测，并将工程现场实测数据在SVM模型的回归预测精度和BP神经网络模型中的回归预测精度进行对比，评价了这类模型的预测精确度和可靠性。

1 支持向量机回归理论

1995年，VAPNIK等[12]提出支持向量机理论SVM。SVM是一种在统计学习理论基础上发展出来的全新机器学习算法，基于VC维(Vapnik-Chervonenkis Dimension)理论和结构风险最小化(Structural Risk Minimization，SRM)原则，通过寻找最优分隔超平面的过程实现对样本数据的分类或者回归预测[13]。最优超平面建立的过程使得模型对于小样本问题仍能较好地适用，并且泛化能力得到保证，支持向量机算法具有较高的准确性及稳定性，成为解决有限样本数据处理、高维模式识别、非线性回归拟合问题的一种新方式。

支持向量机的基本原理是通过寻找一个能将现有样本集按照模式类型分开且能同时满足分类间隔最大的最优分类超平面完成数据处理。对于非线性问题，需将数据映射到高维度的特征空间后围绕选择得到的支持向量(Support Vectors，SV)进行回归分析，进而寻找最优分类超平面，将线性支持向量机的应用推广至非线性解空间。

图1为平面数据高维映射后线性可分示意图，表示了在二维平面线性不可分的两类数据映射至三维空间后可被Z＝KX＋b形式的平面划分，其中X＝{x1，x2}。图1中，x1轴表示第一维度数值，x2轴表示第二维度数值，z轴表示映射后的高维数值。。 其中，xi(i＝1，2，

图1 平面数据高维映射后线性可分示意图

在回归拟合问题上，假设给定一个样本集S＝…，n)为输入变量，由n个d维向量构成；yi为对应的期望输出值。故该样本集回归函数f(x)的形式由式(1)表示为

式中ω∈Rd为权值矢量；b∈R为标量阈值；ω·xi表示ω与xi的点积。求解ω和b的优化问题由式(2)和(3)表示为

式中ε为引入的不敏感因子；C为惩罚因子，表示对超出误差式中达ε的样本的惩罚程度；ξi、ξ*i为松弛变量，是样本偏离不敏感区间ε的上、下限界。

支持向量机数据回归拟合示意图如图2所示，展示了支持向量机算法回归拟合分析的计算规则，坐标中的3条曲线分别为f(x)和拟合区间上、下界。

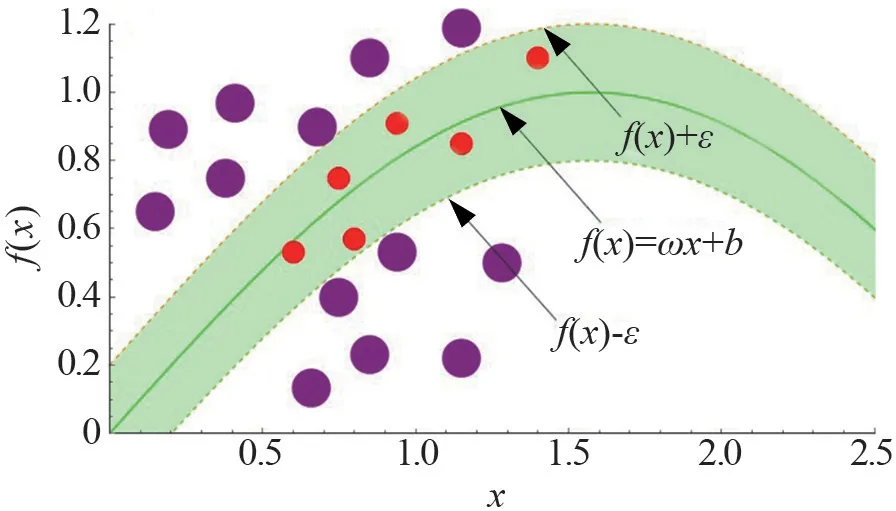
图2 支持向量机数据回归拟合示意图

根据非线性规划对偶性理论，引入拉格朗日乘子建立优化约束方程，将最小约束整理为凸二次规划最大值问题，由式(4)表示为

由最优化理论(Karush-Kuhn-Tucker，KKT)条件可知，令式(4)对ω、b、ξi、偏导为0，可将其转化成对偶形式求解，由式(5)和(6)表示为

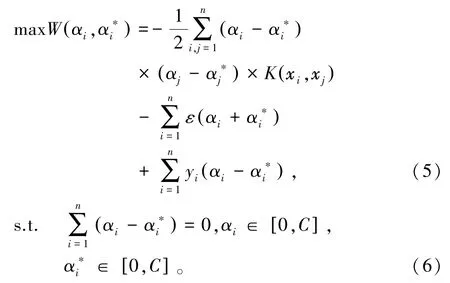
对式(5)的方程进行求解得式(7)为

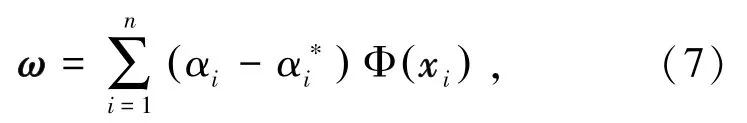
式中K(xi，xj)＝Φ(xi)·Φ(xj)，是支持向量机的核函数。

综上映射操作，可得泛化回归函数，由式(8)表示为

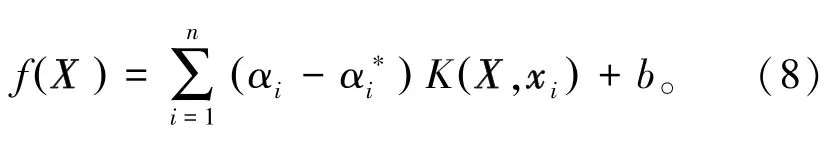
2 GA－SVM组合算法模型

针对地基处理工程问题的数据分析与预测问题，应选取容错性好，可泛化程度高的算法模型。复杂工程回归预测中常应用BP神经网络模型进行分析，BP神经网络模型的研究成果在大样本、多变量、高度非线性预测问题上得到了较高水平的肯定；BP神经网络利用数学关系构建神经元网络结构，并通过对大量样本数据的训练学习，逆向确定修正出各隐含层神经元间的连接强度，基于经验数据的学习过程使其预测准确率达到工程可接受水平；但是其算法存在过分依赖于原始经验数据、较早地收敛于局部极值点、较高频率的过拟合现象等问题。当选择应用优化支持向量机算法预测强夯有效加固深度时，由于该算法通过寻找样本中的支持向量，确定出距离样本的间距最大的超平面而实现数据处理，且基于VC维理论实现矩阵变换使得原线性不可分的数据在足够高的维度空间中线性可分，因此支持向量机具有机器学习算法中最高的样本泛化能力与非线性适应能力，算法即使在小样本的数据分析中仍能发挥出较大的准确度优势。

文章基于计算软件MATLAB平台LIBSVM[14]工具箱编写强夯有效加固深度的预测回归程序，对SVM回归预测进行现实工程数据的仿真分析；同时编程构建BP人工神经网络模型并完成建模、训练、仿真和预测，对同一样本集进行训练，使神经网络模型达到与SVM模型同等的精度水平后，以地基处理工程现场实测数据为例，分析对比GA－SVM与BPANN两种机器学习模型在强夯有效加固深度预测精度上的性能表现。

支持向量机回归试验中拟合结果的精度与算法中数据嵌入维数m、惩罚因子C、损失参数(不敏感因子)ε、核函数K类型及核函数相关参数之间存在一定联系，确定最优的模型参数组合可以使拟合误差降至最低，且满足测试样本的检验精度要求。计算模型中与运算效率、计算精度有关的参数为C、ε和σ，其中C在特征空间中控制模型复杂度和经验误差风险比值，其值越大，SVM对样本数据的拟合程度越高[15]；ε控制样本中支持向量的数量，其取值越大支持向量越少。3个影响参数间相互制约且无明确函数相关性，应用进化启发式寻优算法—遗传算法(Genetic Algorithm，GA)[16]对C、ε、σ共3个参数的取值优化。

支持向量机的遗传算法优化部分具体通过以下步骤实现:

(1)遗传算法参数初始化并定义初始种群

确定种群数目为40，最大迭代次数为250次，交叉率单点交叉法取0.58，变异率取0.01，选择范围取0.9。

(2)确定GA－SVM参数寻优范围并编码

C、ε、σ的寻优区间分别设为[0，60]，[0.000 01，0.1]，[0，10]，将其按二进制形式进行遗传算法的种群染色体基因编码，初始随机产生基因型为该二进制编码序列的种群。

(3)适应度函数定义

设定该模型中种群适应度为SVM回归结果的均方误差。

(4)选择、交叉、变异

根据个体适应度，通过轮盘赌法将具有较低适应度值的个体淘汰，较高适应度值的染色体被复制；以交叉率交换染色体结构中信息以得到子代基因，在种群进化过程中，设定基因突变率以一定概率随机改变染色体编码序列中的基因点。按照遗传进化策略，对种群运用选择、交叉、变异，并逐代进化。

(5)进化终止寻优求解结束并解码

当种群进化代数达到设定的上限时，寻优结束，将求解过程中适应度值最佳的种群解码，得到满足条件的全局最优解C、ε、σ，参数最优化GA-SVM模型建立完成。

使用优化后的GA-SVM算法进行样本集数据回归与测试集数据预测，可以实现SVM算法的理论最优性能。将其应用于具体工程问题，应当有较高的预测精度与泛化能力。GA-SVM算法模型的回归预测流程图如图3所示。

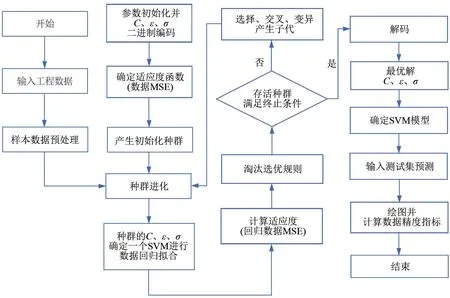
图3 GA－SVM模型回归预测流程图

3 GA－SVM工程数据计算

为了验证GA－SVM回归预测模型在强夯法有效加固深度预测应用上的性能，现从我国地基处理工程现场及相关文献资料中选取36个强夯地基处理样本集合，确定其输入参数为地基土的干重度、含水量、夯锤夯击能量和夯锤面积，期望其输出值为有效加固深度一项。此样本数据具有较高的离散性和独特性，拥有一定程度的代表性。采用选取的36个工程样本[17－18]经过数据归一化处理后组成的训练样本集(见表1)对模型进行训练，直到模型针对训练样本集的训练预测结果的均方误差降低至设定范围后，应用该模型进行全新测试样本集的仿真预测。

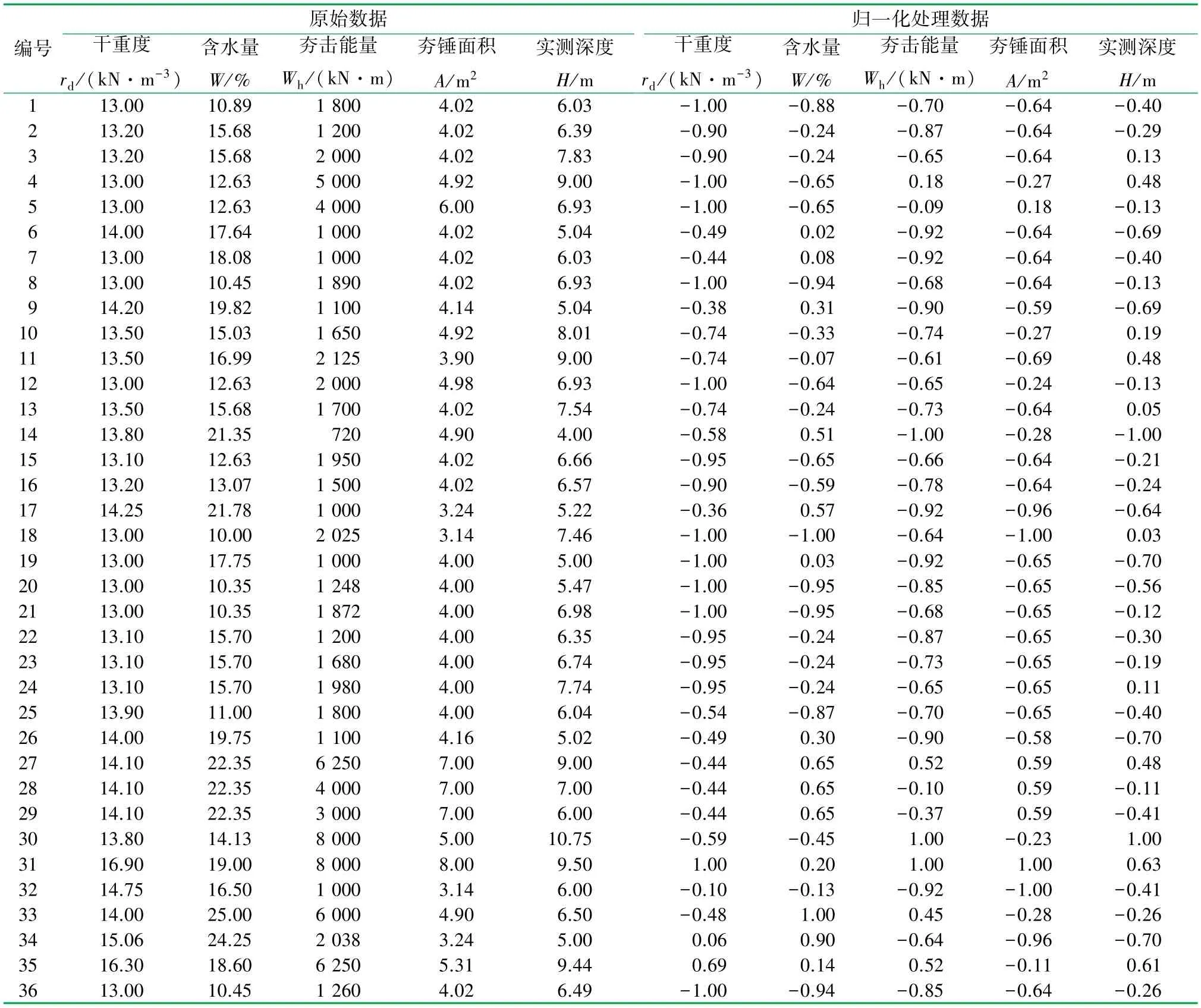
表1 实测原始数据及归一化处理数据结果表

GA－SVM的完整应用过程具体分为以下步骤:

(1)对输入数据归一化处理，将不同量纲的数据按种类分别归一化至区间[－1，1]内，可由式(9)表示为

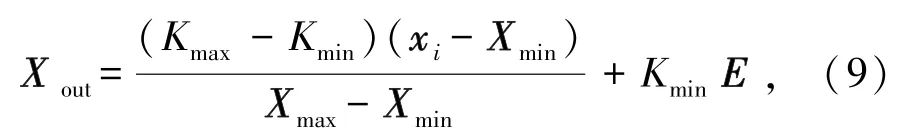
式中Kmax、Kmin分别为1、－1；Xmax、Xmin分别为实测原始数据每列的最大值、最小值组成的矩阵；Xout为归一化值。

(2)将36组多维数据参数输入初始化后的GA-SVM参数寻优环节，当均方误差低至阈值时，输出C、ε、σ值，以确定具体的SVM模型。

(3)预测深度值逆归一化，将数据“放大”回原量纲数量级，将该SVM模型对于样本集的拟合程度与精确率列式计算；将结果绘图展示，观测误差偏离程度与拟合可信度。

(4)选取全新工程测试数据集代入GA-SVM预测模型以测试其对全新样本的回归能力与泛化水平，计算预测准确率。选取深度数据相对误差R与平均绝对均方误差A反映结果的精度，分别由式(10)和(11)表示为

式中yi为预测值，为实测值。

归一化数据输入支持向量机后，支持向量机3参数C、ε、σ经优化后取值分别为3.00、0.00、和1.44。参数组成的支持向量机对原始36个五维数据的拟合精度表征为均方误差值等于0.005，平方相关系数为0.973；重复优化过程至结果收敛。均方误差和相关系数的数据表明，GA－SVM对训练数据的回归拟合程度达到相当精确的预测程度。使用SVM训练阶段未学习过的工程实测测试数据集代入检验，观测该模型能否对于工程实测数据的预测达到与真值相近的准确率水平。

4 GA－SVM工程实例测试

校验步骤中用于测试的实测数据[17]来自山西省化肥厂工程、化工部第二化工建设公司、山西化肥厂、化工部北京重机公司、化工部第二设计院及太原工业大学等。测试数据见表2，其中A、B、C组工程场地及土质等具体如下:

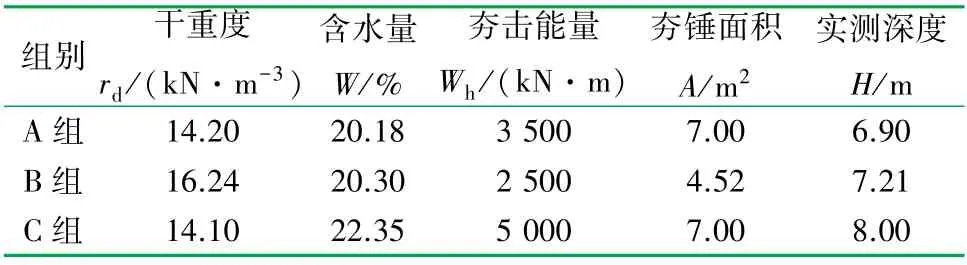
表2 测试数据表

A组:山西化肥厂湿陷性黄土地基强夯处理工程，Ⅰ区，湿陷性黄土地质，干重度为14.2 kN/m3、含水量为20.18%、强夯夯击能量为3 500 kN·m、夯锤面积为7.00 m2，其实测有效加固深度为6.90 m(该深度数据不代入预测模型，用作最终预测值的验证与误差检验)。

B组:场地Ⅱ区，湿陷性黄土地质，干重度组16.24 kN/m3、含水量为20.30%、强夯夯击能量为2 500 kN·m、夯锤面积为4.52 m2，其实测有效加固深度为7.21 m。

C组:场地Ⅰ区，湿陷性黄土地质，干重度为14.10 kN/m3、含水量为22.35%、强夯夯击能量为5 000 kN·m、夯锤面积为7.00 m2，其实测深度为8.00 m。

检验步骤中，将GA-SVM的预测数据与BPANN模型的对比，BP-ANN基于MATLAB平台编程实现，为保证对比有效客观，选用训练至同GA-SVM一样误差(均方误差为0.005)水平的BP－ANN进行仿真预测。其中，BP－ANN模型选用含3个隐含层共50个神经元构成的误差反向传播网络进行训练，模型简图如图4所示。

图4 含3个隐含层的ANN结构图

图5 为BP－ANN模型和GA－SVM模型的计算深度与夯击能量关系图。对GA－SVM模型与BPANN模型多次重复仿真预测，选取具有代表性且客观可信的数据，并对比了两个模型计算测试样本集的误差，见表3。

表3 模型计算测试样本集的误差对比表

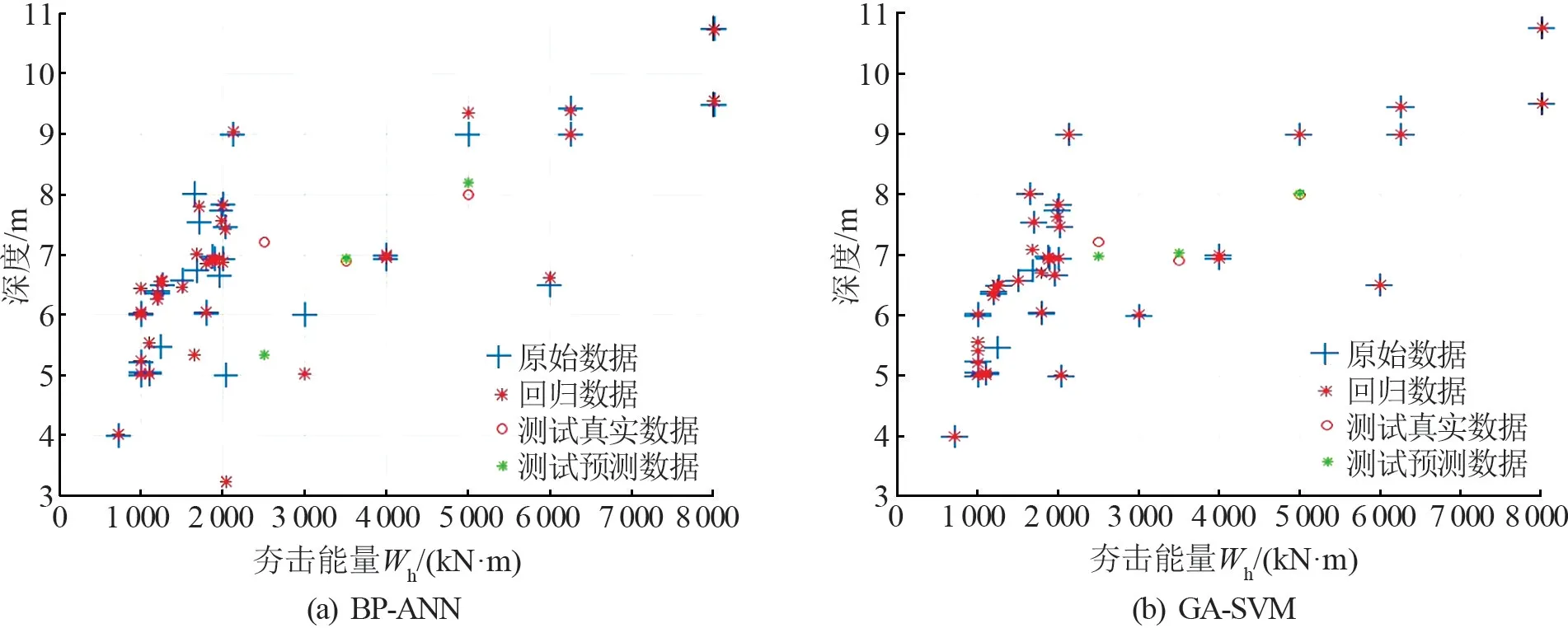
图5 不同模型计算深度与夯击能量关系图

计算数据相对误差的绝对值≤3%时，说明该模型精度较高[19]。由表3可知，GA－SVM的测试集预测值最大偏离真值为3.28%，其平均偏离为1.72%，其预测性能能够满足较高的精度且算法稳定性较好，反映出其经小样本学习后的模型泛化能力同样具有较高可信度；而BP－ANN预测模型，大量的神经元组成的处理非线性数据的网络结构对训练数据量要求很高，从结果数据中反映出其对于测试样本的预测精度偏离较大，波动性过强，存在过拟合现象。GA－SVM和BP－ANN测试集预测的均方误差分别为0.024 1、1.184 9，GA－SVM模型预测的均方误差仅为BP－ANN的2%，达到了不同量级的精度，试验过程多次重复后表明结果客观可信，故GA－SVM模型的工程问题的泛化精度得到了有效地保证。

5 结论

通过编程构建的应用遗传算法优化支持向量机理论的数值拟合、回归预测模型准确、高效地实现了对强夯有效加固深度的计算分析，并将模型应用到工程问题中，得到的主要结论如下:

(1)遗传算法优化的支持向量机算法模型能够在训练样本上实现准确的回归拟合，数据拟合精度达到均方误差值0.005，平均相关系数为0.973。

(2)GA－SVM模型对测试样本数据预测精度较高，预测结果均方误差为0.024 1，相对误差<3%，优于BP神经网络模型预测结果。数据证明，基于遗传算法优化的支持向量机模型在强夯有效加固深度问题上的拟合精度更高，预测准确性更强。