ISO 10113:2020标准中若干技术问题的验证
凃应宏, 李荣锋, 尚 伦
(1.宝钢股份武钢有限技术中心, 武汉 430080;2.东莞材料基因高等理工研究院, 东莞 523808)
塑性应变比(r值)与拉伸应变硬化指数(n值)均可以用来表征金属材料的成形能力。r值反映了材料在长度、宽度和厚度3个方向的变形能力;n值表征材料的形变强化能力。在实践中,这两个指标往往是用同一件试样在单向加载条件下测定的,但数据表明:作为材料特性参数,n值具有较好的一致性,而r值却有明显的离散性。相关工作人员为提高r值测试的准确性也在不懈地探索和努力[1-4]。
长期实践表明,影响金属薄板r值测试数据准确性的因素众多,除了材料本身性能的差异外,试样的取向、平整度、加工/形位公差、试样夹持方式、尺寸测试、引伸计、加载过程的平顺性等因素也会影响最终的测试结果。r值测试的核心应该是真实、准确地测试出试样的纵向变形和横向变形,并且在测试的同时不扭曲两者之间的(几何上以及逻辑上)对应关系。
在r值测试技术的发展初期,受制于当时的科技发展水平(引伸计未得到广泛普及),在实际操作过程中需要停机、卸载,再取下试样,由人工利用比长仪或其他量具对试样的纵向变形和横向变形分别进行测试。该方法对试样的纵向变形测试精确,但效率非常低下,难以满足大生产条件下批量测试的要求。
随着科学技术的发展,尤其是较为轻便的电子引伸计的逐步应用,r值测试技术进入到第二阶段,即半自动加载测试阶段。该阶段试样的纵向变形由纵向引伸计实时测试,当达到约定值后停机(但不卸载),因为停机时试样的纵向变形已知,此时仅需人工利用千分尺在加载条件下对横向变形进行测试。r值测试从该阶段起需在加载条件下进行。为了验证加载测试的科学性和准确性,早在制定国标GB/T 5027—1984 《金属材料 薄板和薄带 塑性应变比(r值)的测定》时,国内就开展了相关研究工作[5],当时的数据已经表明,加载、卸载阶段所测得的r值没有显著差异。
为了解决数据的离散性问题,r值测试技术也在不断地发展和完善。在新颁布的ISO 10113:2020MetallicMaterials-SheetandStrip-DeterminationofPlasticStrainRatio,theInternationalOrganizationforStandardization标准中,对试样的横向变形测试问题也给出了新的解决方案。与此同时,将ISO 10113:2006中r值计算公式的修改提上日程。ISO 10113标准的修订者认为:既然r值是反映材料塑性变形能力的参数,那么在计算公式中可以扣除弹性变形;从具体的操作层面看,受离散性影响的加载测试方式也可以转变为卸载测试方式。
标准GB/T 5027—2016的修订者对上述观点持保留态度[6],这是因为目前r值测试的主要问题在于数据的过度离散,通过弹性扣除无法解决该问题。利用软件扣除弹性变形仅是一种形式上的虚拟性卸载,与真实的人工卸载测试有着本质上的区别。只有经过大量试验数据的积累,证明新算法的结果与人工测试值更加接近,才能消除工作人员的疑虑。
1 验证试验
为了对ISO 10113:2020的技术内容有一个准确、客观的认识,2020年12月至2021年4月,全国钢标委力学分技术委员会组织国内相关单位开展了《金属材料 薄板和薄带 塑性应变比(r值)的测定》的验证活动。该项活动主要针对人工、半自动和全自动3种测试方式的准确性和一致性进行验证,并围绕试样的不均匀变形、是否扣除弹性应变等问题进行了讨论。这是数十年来,国内组织的最大规模的涵盖3种测试方式的r值测试验证活动,共计有15家实验室参加了该工作(见表1),这些实验室均长期从事金属薄板r值的测试工作,在业界具有广泛的代表性。参与验证活动的设备也基本上代表了当前国内的主流水平。
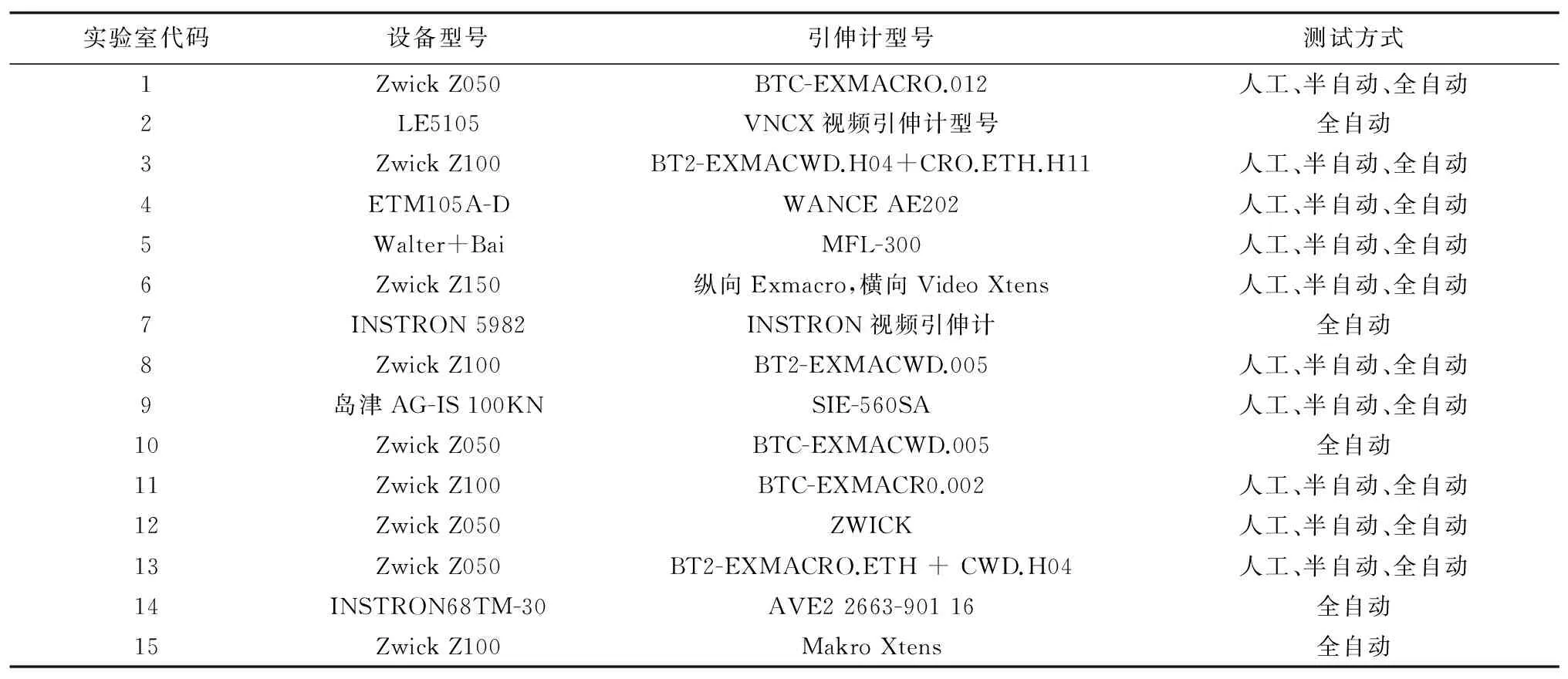
表1 参加验证活动的实验室和设备概况
验证试验使国内相关单位对ISO 10113:2020标准中的一些关键条文有了更加清晰、全面的认识,为下一步启动修订GB/T 5027的工作打下了良好基础。同时验证工作对推动国内r值测试技术的发展,促进国内设备水平的提高也具有重大意义。
试验主要对BUSD-A、BUSD-B、430不锈钢以及6082铝合金等4种不同规格的试样进行验证试验(其中BUSD-A和BUSD-B取自同一块钢板)。4种试样的外形尺寸和标距各异,约定应变水平也存在不同(见表2,其中a0为试样原始厚度,b0为试样原始宽度,L0为原始标距,Lc为试样平行段长度,Lt为试样总长度)。试样的加工公差和形位公差均满足ISO 10113:2020标准的要求。4种试样的约定应变水平为r5,r15,r8。
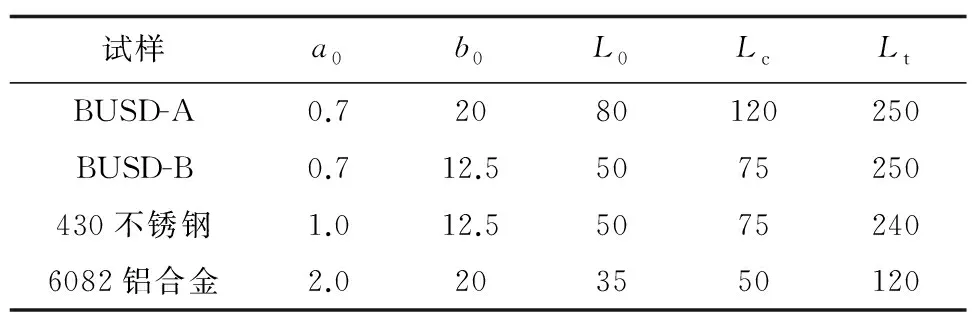
表2 验证试验试样的参数 mm
2 数据分析
2.1 对人工、半自动和全自动3种方式测试结果的分析
15家实验室中有10家参加了3种测试方式的验证,5家仅参加了全自动方式的验证。由于各个实验室参与验证的项目和试样数量均存在差异,因此后文各图表中所列的实验室数据存在8~35组不等的情况。2.1节至2.4节中所指的自动测试方式均未扣除弹性变形。
BUSD-A试样的数据分布如图1所示(L0=80 mm)。从图1整体上看,除了存在一个明显异常的半自动测试数据3.40以外,大部分数据为2.27~2.99。如果进一步细分,自动测试结果为2.40~2.99,平均值为2.617;人工测试结果的收敛性优于自动测试结果的收敛性,人工测试结果为2.40~2.70,平均值为2.537;而半自动测试结果为2.27~3.40。人工测试结果比自动测试结果整体偏低。如果在自动测试时对弹性变形进行扣除,则结果偏高0.15左右。

图1 BUSD-A试样的数据分布
BUSD-B试样的数据分布如图2所示(L0=50 mm)。由图2可知,全自动测试结果仍然为2.39~3.06,平均值为2.635;人工测试结果明显收敛,为2.41~2.77,平均值为2.542;半自动测试结果为2.38~2.65。整体看,BUSD-B试样与BUSD-A试样的数据分布规律是类似的,虽然存在数据波动,但人工、半自动和全自动测试结果的均值基本一致,其中人工和半自动测试结果约为2.55,全自动测试结果约为2.65。如果在自动测试时对弹性变形进行扣除,则测试结果更加远离人工测试结果。

图2 BUSD-B试样的数据分布
另外两种材料的数据分布规律与BUSD试样的数据分布规律基本一致。430不锈钢试样的数据分布如图3所示(L0=50 mm)。6082铝合金试样的数据分布如图4所示(L0=35 mm)。

图3 430不锈钢试样的数据分布

图4 6082铝合金试样的数据分布
对ISO 10113:2020标准中所列人工、半自动和全自动3种测试方式进行验证,得出以下结论。
(1) 虽然存在数据的波动,但人工、半自动和全自动3种测试结果的平均值较为接近。对于BUSD材料试样,其人工和半自动测试值约为2.55,全自动测试值约为2.65,三者之间的差异小于0.10;对于430不锈钢试样,三者差异小于0.10;对于6082铝合金试样,三者差异小于0.04。
(2) 由于BUSD-A和BUSD-B试样截取自同一块钢板,虽然其外形尺寸和应变不同,但人工测试结果却是基本一致的。这进一步说明r值作为一个材料特征参数,在塑性变形期间控制着材料的纵向和横向变形,试样形状和应变不会对r值造成影响。
(3) 半自动和全自动测试结果都存在明显的离群数据;相对而言,人工测试结果不存在明显的离群数据,这是因为后者受到的影响因素相对较少。
2.2 视频引伸计测试结果分析
一般情况下,业内人士认为人工测试r值结果偏低是试样的不均匀变形造成的。这是由于人工测试时,测量部位除了试样中间区域外,还包含了标距两端,受过渡弧的约束,标距两端的变形量有时会低于中间区域。为了尽可能降低试样不均匀变形的影响,GB/T 5027—2016标准要求应确保Lc≥(L0+2b0),而ISO 10113:2020标准除了要求进一步增加试样平行段长度Lc外,还提出了基于视频引伸计的“多线测试”解决方案。
参加验证试验的15家实验室中有4家配备了视频引伸计,其中2家实验室另外还提供了单线和多线之间的比对数据,视频引伸计的测试结果如图5~7所示。由图5~7可知:视频引伸计中的多线测试结果仍然呈现出较大的离散性,BUSD-A试样的多线测试结果为2.40~3.00,三线测试结果为2.20~2.55;BUSD-B试样的多线测试结果为2.40~3.10,三线测试结果为2.40~2.50。从两家实验室提供的三线和多线测试结果看,BUSD材料试样的三线测试结果多数情况下比多线测试结果低0.10左右,少数情况下两者基本一致。对6082铝合金试样而言,三线测试结果偏高。

图5 BUSD-A试样的视频引伸计测试结果(L0=80 mm)

图6 BUSD-B试样的视频引伸计测试结果(L0=50 mm)

图7 6082铝合金视频引伸计测试结果(L0=35 mm)
从视频引伸计的实际测试结果看,多线测试方式同样无法有效避免数据的离散性问题。实际上验证试验中大部分的离散数据都来源于视频引伸计,这需要引起足够重视。虽然在理论上,该方案有其科学性和先进性的一面,但现阶段测试的准确性尚有待提高。三线测试结果有时比多线测试结果低,有时却偏高,这一点也预示着试样的不均匀变形问题仅是一个可能性事件,而非确定性事件。
2.3 试样不均匀变形的验证
为了证实试样是否普遍存在不均匀变形,验证试验对试样变形前后的尺寸进行了人工实测,测试部位分别位于试样中部以及靠近过渡弧的标距两端。有10家实验室参与了该项验证试验,数据如图8~10所示。

图8 BUSD-A试样不同部位的横向应变(b0=20 mm)

图9 BUSD-B试样不同部位的横向应变(b0=12.5 mm)
从BUSD-A试样的数据看,在应变水平为5%时,有少部分实验室的两端测试值偏低,但大部分实验室的中部测试值偏低。从BUSD-B试样的数据看,在应变水平为15%时,两端测试值偏低。图10中,部分实验室的两端测试值偏低,但也有少数实验室得出了相反的结果,即中部测试值偏低。

图10 430不锈钢试样不同部位的横向应变(b0=12.5 mm)
总体上看,不同部位横向应变的差异并不明显,标距两端的横向应变也并不总是偏低。一方面可能是受到人工测试的准确度限制,另一方面也说明试样的不均匀变形并不确定。
试样的横向不均匀变形对r值的影响可以通过理论分析进行预测。
(1)r值对横向应变的测试极其敏感,实测r值与理论值的偏离、横向应变的偏离均呈正相关。这种偏离的程度越低,则实测r值曲线收敛程度越理想(见图11)。对一个r值为2.6的理想试样而言,在应变水平为5%时:如果横向应变eb实测值存在±0.02%的偏离,则r值为2.55~2.65;如果eb实测值存在±0.05%的偏离,则r值为2.46~2.74;随着应变的增加,这种影响将逐步减弱,在应变为15%时,r值为2.55~2.65。
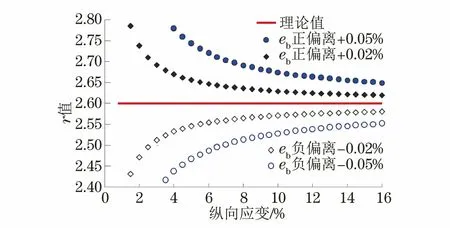
图11 横向应变eb不同偏离对r值为2.60的影响
(2) 随着材料沿厚度方向变形能力的减弱(r的理论值降低),横向应变测试对r值的影响将整体性减弱。对于一个r=1.7的理想试样(见图12),在应变水平为5%时:如果eb实测值存在±0.01%的偏离,则r值为1.68~1.72;如果eb实测值存在±0.05%的偏离,则r值将扩大到1.62~1.78;随着应变水平的增加,这种影响将逐步减弱,在应变水平为15%时,r值可缩小到1.66~1.74。
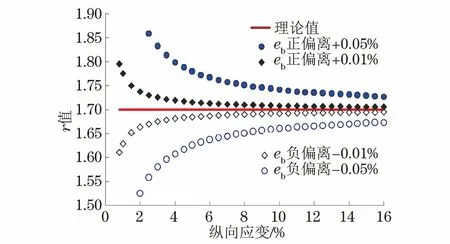
图12 横向应变eb不同偏离对r值为1.70时的影响
从实测数据看,即使标距两端和中间部位的横向应变(三者平均值)比单纯在中部测得的应变低,两者间的偏离在多数情况下也小于0.02%。结合图11,12可知,这么小的差异不会对r值的测试结果造成太大影响。这至少说明r值的人工测试结果整体性偏低不单纯是试样的不均匀变形造成的,可能还存在其他原因。
2.4 人工测试与自动测试数据存在差异的其他原因
如前所述,随着可变标距全自动引伸计测试技术的引进和普及,r值的测试进入到一个全新的发展阶段。但应该注意该类引伸计存在着结构性缺陷:首先,对横向引伸计而言,除了监测范围过窄之外,还存在自适应问题,即当试样纵轴与加载系统纵轴存在偏离时,引伸计测得的横向变形偏大;其次,纵向引伸计标距Le存在准确性和稳定性问题。
一般情况下,如果采用人工装夹方式,试样的纵轴与加载系统的纵轴难以重合,具体如图13所示。

图13 试样纵轴发生偏转示意(以试样宽度变形量Δb为例)
进行人工测试时,试验前b0=2×LFJ,卸载后测得Δb1卸=2×LIJ,因此人工横向应变为
(1)
当采用横向引伸计测试时,试验前Le=2×LFJ,停机时刻Δb1加=2×LTK,因此引伸计的横向应变为
(2)
如果将弹性变形LTH扣除,则Δb1加-Δb弹性=2×LHK,引伸计横向应变可修正为
(3)
可见,在试样纵轴发生偏转的情况下,即便扣除弹性应变,由于
(4)
在理论上都无法确保eb塑性=eb人工,如果不扣除弹性应变,则
(5)
与此同时,试样的偏转不会对纵向引伸计的测试造成类似影响,这是由于纵向、横向应变测试对原始标距Le的定义不同,因此卸载后人工测得的试样长度方向应变eL人工与引伸计测得的试样长度方向应变eL引伸计较为接近。但对于横向应变,人工测得的eb人工比引伸计测得的纵向应变eb引伸计低,即使考虑弹性应变的影响,大部分的eb人工也比eb引伸计低0.1%左右。图14为卸载后测得BUSD-B试样的eb人工与eb引伸计。

图14 卸载后测得BUSD-B试样的eb人工与eb引伸计(L0=50 mm)
理论分析表明:对于BUSD-B试样,如果试样纵轴的偏转角度超过6°,那么人工测得的Δb1卸可能比引伸计测得的Δb1加偏低0.007 mm左右,这会造成人工测得的r值整体偏低0.05;偏转角度如果超过8°,那么人工测得的Δb1卸偏低0.012 mm,这会造成人工测得的r值整体偏低0.10。因此,除非试样纵轴与加载系统纵轴完全重合,否则人工测试r值整体偏低。
综上所述,人工测试r值偏低的原因除了试样的不均匀变形外,还有可能是横向引伸计无法适应试样的偏转。除非采用自动装夹机械手,否则对于人工装夹试样,全自动引伸计未能很好地解决这一问题。
除了横向测试外,自动引伸计还存在纵向标距Le的准确性和稳定性问题。为了灵活地调节标距Le,该类引伸计采用了特殊的杠杆式平衡结构。客观地说,Le的准确性和稳定性并没有带插销的手动引伸计高,只要纵向标距Le与理想值存在偏离,就会产生纵向变形的测试误差,更严重的是会造成指向性错误,从而扭曲纵向和横向变形两者之间的对应关系,这也是r值数据波动的原因之一。
为了说明纵向引伸计标距Le偏差对r值测定的影响,假设存在编号为B~F的5支纵向引伸计,其名义标距Le均为50 mm,其中C,E为0.5级引伸计,B,F为1级引伸计。如果使用的是编号F的1级引伸计,由于标距存在负偏差-1.0%,那么其实际标距Le″为49.5 mm。经推算可知,编号F引伸计测得的15%应变与实际情况存在一定偏离,此时试样的实际变形应为15.15%(见表3,ΔL为试样长度变形量)。

表3 纵向引伸计Le偏差所导致的指向异常
但即使编号为F的纵向引伸计所指向的15%应变与试样实际产生的15.15%应变存在偏离,测试系统也无法识别并修正这种偏离。这种指向性错误将导致系统发生“逻辑错位”,即纵向引伸计所指向的15%应变水平与横向引伸计感知的15.15%实际应变水平不对应,但系统仍错误地将两者认定为一对数据组代入公式,计算出一个错误的结果。与此类似,可以将表3中编号为B~F的引伸计依次装夹到理想试样上,上述关系错位造成的影响如表4所示。
从表4可以看出,不考虑其他影响因素,如果试样装夹的是编号分别为C,E的0.5级引伸计,则r值为2.56~2.65;如果试样装夹的是编号分别为B,F的1级引伸计,r值为2.52~2.69。从这些数据可以看出,只要纵向引伸计的标距Le与理想值存在偏离,那么r值的波动将不可避免。在实际测试过程中,肯定还叠加有其他的影响因素,r值的波动性有可能缓解也可能进一步加剧。

表4 测试系统逻辑性错位对r值的影响
r值的准确性完全取决于试样的纵向变形和横向变形能否被准确地测试出来,并且在测试的同时,不扭曲两者之间(几何上以及逻辑上)的对应关系,目前广泛采用的全自动引伸计可能存在着如下几个问题。
(1) 对人工装夹试样而言,试样纵轴的偏转是不可避免的,如果引伸计无法适应这种偏转,就可能扭曲了纵向变形和横向变形之间的几何关系,引伸计测得的横向变形偏高。由于r值对试样的横向变形极其敏感,并且两者呈正相关,因此自动测试得到的r值存在被高估的风险。
(2) 纵向引伸计实际上担负着“测试”和“指向”的双重职责,如果纵向标距Le与理想值存在偏离,则不仅会产生测试误差,更严重的是“指向性错误”扭曲了纵向和横向变形两者间的逻辑关系,这也是r值数据波动的主要原因之一。如果想减小这种负面影响,就要提高纵向引伸计标距Le的准确度和长期运行的稳定性,这对设备生产厂家来说是一个挑战。
(3) 对设备使用者而言,在日常工作中,应该注意采取措施对自动引伸计标距Le进行维护和主动修正,否则其计量特性超出规定是完全有可能的。
2.5 弹性变形对r值的理论影响
在r值的计算公式中扣除弹性变形最早始于标准ISO 10113:2006,这种扣除仅是一种形式上的虚拟性卸载,其与真实的人工卸载测试有着本质上的区别。为了便于后续开展对验证数据的分析,首先利用ISO 10113:2020的新公式进行理论推算,找出弹性变形对r值的一些理论性影响。
(1) 扣除弹性变形后,r值曲线自上而下随应变水平的增加逐步向理想加载值收敛。材料的屈服强度等级越低,则弹性变形越小,r值曲线的分布更靠近内侧,曲线收敛得越早,收敛程度越理想。
(2) 应变水平越小,弹性扣除对r值造成的理论影响就越大。以BUSD-A试样为例,一个r值为2.6的理想试样在应变为5%时:如果材料的屈服强度等级为200 MPa,则r值将偏高0.10;如果屈服强度提高到600 MPa,则r值将偏高0.35;随着应变水平的增加,这种影响将逐步减弱,在应变为15%时,两者间的理论差异可减小到小于0.05(见图15)。
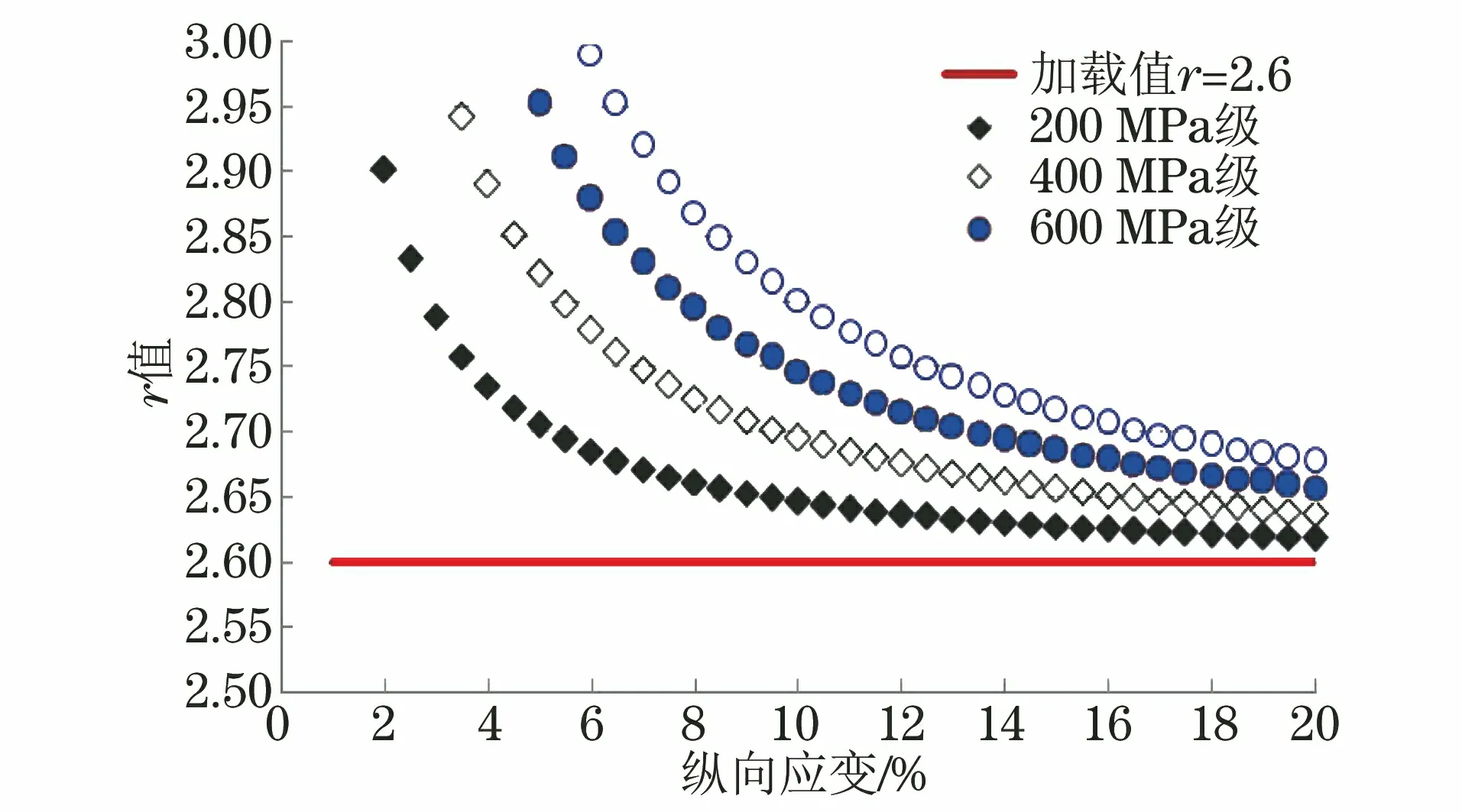
图15 BUSD-A试样屈服强度等级对r值的理论影响
上述规律是基于ISO 10113:2020标准中钢铁材料泊松比ν为0.3推导出的。如果在软件中采用实测的泊松比ν,将使弹性变形扣除的问题更加复杂化。泊松比越大,曲线的收敛性越好,泊松比越小,曲线的收敛性越差。
6082铝合金试样强度等级对r值的理论影响如图16所示,曲线在更低的应力下会向理想值收敛。在应变为5%时,即使材料的强度等级高达2 000 MPa,经过扣除后的r值理论上也仅偏高0.015。

图16 6082铝合金试样强度等级对r值的理论影响
验证试验的数据与上述理论推算结果基本相符。BUSD材料试样弹性变形对r值实际影响如图17~18所示。由图17~18可知,扣除弹性变形后,r值会整体性偏高,5%小变形情况下偏大0.15左右;在15%大变形情况下,偏大值<0.05。可见,应变水平越低,则弹性扣除对r值造成的影响就越大。但随着应变的增大,这种影响将明显减弱,对强度级别低于400 MPa的材料,15%应变下两者间的理论差值通常可减小到0.05以内。但在图17~18中,也有少量数值与上述规律存在差异,这一方面可能是因为弹性段斜率mE存在差异,另一方面可能是因为部分软件用实测泊松比计算。

图17 BUSD-A试样弹性变形对r值的实际影响
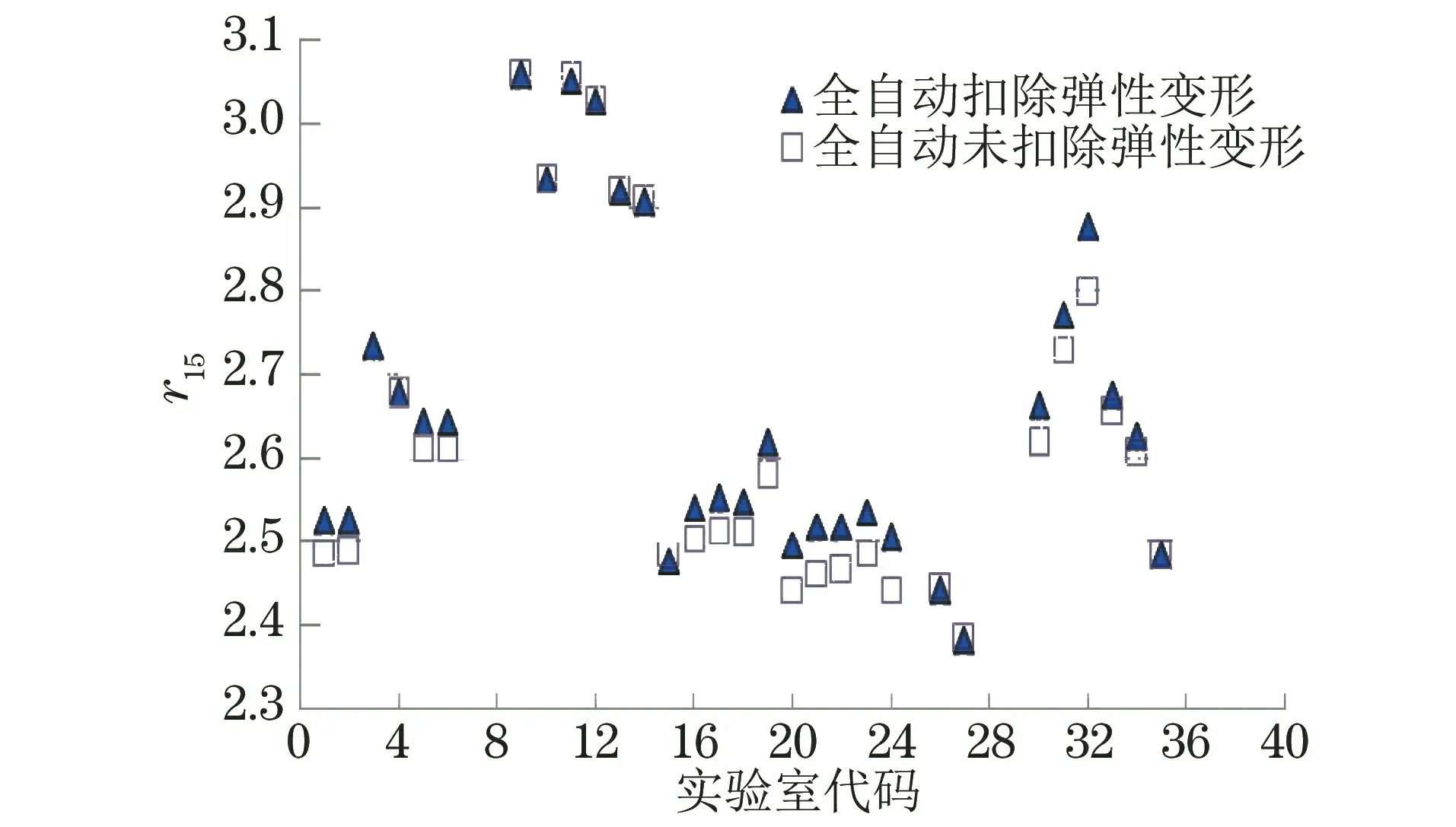
图18 BUSD-B试样弹性变形对r值的实际影响
6082铝合金试样弹性变形对r值的实际影响如图19所示。由图19可知,6082铝合金试样扣除弹性变形后的r值仅偏高0.01左右。这也证实,如果材料沿厚度方向的变形能力有所减弱,那么弹性变形扣除对r值的影响将整体减弱。对r为0.6的理想试样而言,弹性变形的影响基本可以忽略。
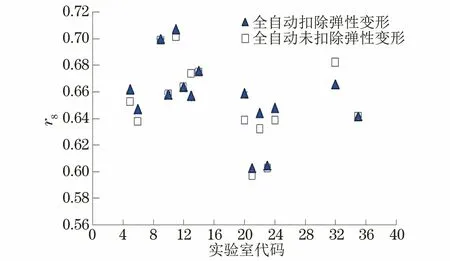
图19 6082铝合金试样弹性变形对r值的实际影响
ISO 10113:2020标准希望借助计算公式对弹性变形进行扣除,通过这样的虚拟性卸载,可在理论上保证全自动、半自动和人工测试方式的统一,即经过软件扣除弹性变形后的r值与人工测试值更加接近,但验证试验结果如下所述。
(1) 加载条件下的r值与人工测试值较为接近,经软件扣除弹性变形后的r值反而有整体偏高的趋势,在低应变时这种差异尤为明显。这说明在真实卸载的情况下,弹性变形仅是影响r值结果的众多因素之一。
(2) 结合BUSD-A和BUSD-B材料的人工测试数据可知:r值是一个控制材料纵向或横向变形的特征参数,在5%~15%的整个塑性变形区间,可以保持一个相对恒定的r值2.55,如果在5%的低应变下对弹性变形进行扣除,r值将提高到2.70,这会对试验人员造成误导。
3 结语及建议
(1) 虽然r值有波动,但人工、半自动和自动3种测试结果的均值较为接近。整体上看自动测试结果的离散性最大,人工测试结果的离散性最小。人工测试结果虽然在横向尺寸的测试精度上比自动测试结果略差,但在纵向尺寸测试精度上有明显优势,并且在测试的同时不会扭曲纵向和横向之间的(几何以及逻辑上)对应关系。
(2) 在自动测试时,纵向引伸计实际担负着“测试”和“指向”的双重职责,由于纵向引伸计存在的“指向性”错误会造成纵向和横向变形两者间的逻辑关系错位,这也是r值波动的主要原因之一。
(3) 从视频引伸计的实际应用效果看,无论是视频引伸计的三线法或是多线法,都无法有效避免数据的离散性问题。
(4) 人工测试虽然效率低,且难以适应大生产条件下的批量测试,但其准确性和可靠性是半自动和全自动方式无法比拟的。
(5) 在加载条件下不扣除弹性变形测得的r值与人工测试r值更加接近,而扣除弹性变形后的r值反而有整体偏高的趋势,那么在国标GB/T 5027—2016中保留传统的r值计算公式还是有必要的。
(6) 需要了解引伸计纵向标距Le的重要性。
(7) 结合半自动(卸载)测试方式对试样的变形尺寸开展检查是非常有意义的,借助这种可重复、可再现的方式,可以便捷地确定影响r值测定的关键因素。
致谢
全国钢标委董莉教授和侯慧宁工程师组织了此次能力验证比对活动,参加验证的单位有:宝钢股份武钢有限技术中心、宝钢股份武钢有限质检中心、宝钢股份中央研究院、宝钢股份检化验中心、广州汽车集团股份有限公司汽车工程研究院、本钢技术研究院、西南铝业(集团)有限责任公司技术中心、广州海关技术中心、山西太钢不锈钢股份有限公司技术中心、国标(北京)检验认证有限公司、首钢集团有限公司技术研究院、力试(上海)科学仪器有限公司、深圳万测试验设备有限公司、英斯特朗试验贸易(上海)有限公司、兹韦克罗睿试验机科技(上海)有限公司。
宝钢股份湛江钢铁、北京有色院和太钢不锈为验证工作提供了试验样品,武钢有限质检中心也给予了大力支持,在此一并致谢!

