结合二维压缩感知和混沌映射的双图像视觉安全加密算法

蒋东华,朱礼亚,沈子懿,王兴元,陈颖频

(1.长安大学信息工程学院,710064,西安;2.长安大学电子与控制工程学院,710064,西安;3.大连海事大学信息科学技术学院,116026,辽宁大连;4.闽南师范大学物理与信息工程学院,363000,福建漳州)

随着网络、通信和多媒体技术的日益发展,数字图像以其承载信息量大、形象直观等特点,被广泛地应用于国防、经济、医学及民生等各个领域。然而,在信息共享便捷化、智能化的当下,图像在传输和存储过程中也存在着诸多安全隐患,如黑客利用网络漏洞非法窃用用户信息,窃取商业和国家机密等。因此,如何对图像的信息进行有效保护,对于个人、企业乃至国家的信息安全都具有重大的意义和研究价值。

在图像加密的实际应用场景中,往往存在信道传输带宽和存储空间受限等客观条件制约。鉴于此,将压缩感知模型与经典混沌加密技术相结合,可实现对明文图像的同步压缩和加密,以有效减少数据传输、存储和处理的压力[1-2],已成为当前信息安全领域的研究热点。例如:龚黎华等基于混沌理论、并行压缩感知和Arnold变换构建一种有效的图像压缩加密算法[3],以降低密文图像中相邻像素点之间的相关性;周南润等结合共稀疏表示和随机数置乱设计一种高效的双图像压缩加密算法,并采用二维Logistic映射来构建测量矩阵以减轻传输密钥的负担[4]。此外,通过结合混沌控制的二维压缩感知和信息熵,甘志华等提出了具有高安全性的彩色图像加密算法[5]。然而,以上加密算法均是将明文图像转换为无视觉意义的类噪声密文图像,此类具有特殊视觉特征的数字图像更容易引起攻击者的注意,从而受到诸如暴力破解,统计分析以及选择明文分析等攻击[6]。

为此,研究者们利用先加密后嵌入的方式,生成具有视觉安全的密文图像,对明文图像的数据和外在表现形式进行双重保护。Bao等将图像加密之后嵌入到载体图像之中[7],但由于缺少压缩环节,生成的密文图像的尺寸是明文图像的4倍,需消耗额外的存储空间和传输带宽。为了解决该问题,文献[8-9]在Bao的框架中引入压缩感知模型,分别提出了两种具有视觉意义的图像加密算法。文献[8]首先通过三维离散Cat混沌映射构建测量矩阵,对明文图像的小波系数进行压缩测量,再在空间域上将秘密信息随机地嵌入到载体图像中;文献[9]设计了一种结合并行压缩感知和整数小波域嵌入的图像视觉安全加密算法,在频域上实现了秘密信息的嵌入。以上两种算法均在保持密文图像尺寸不变的前提下,实现了单幅明文图像的视觉安全加密。

通过以上分析可知,在基于压缩感知和混沌系统的图像加密算法中,混沌系统主要用于生成加密密码流和构建满足有限等距性质的测量矩阵[10-11],其特性将直接影响到加密算法的安全性和计算复杂度。现有的研究中多数采用高维的超混沌系统,以获得可观的安全性能增益,但同时也伴随着更大的计算开销,因此需要对混沌系统的构造进行优化,力求在算法的安全性和效率之间实现更好的均衡。另一方面,受压缩率和嵌入信息容量等因素的制约,现有的单图像视觉安全加密算法已无法满足大批量数据的高效处理需求。

为解决以上问题,本文设计了一种新颖的双图像视觉安全加密算法。首先,从算法安全性和计算复杂度之间的均衡性出发,对一维Chebyshev混沌映射进行了改进,即在原有映射中引入一非线性项,可在保证算法安全性的同时有效地减少计算开销;利用二维压缩感知和最低有效位嵌入技术,对两幅明文图像在两个方向上依次进行压缩,并分别嵌入到载体图像的像素值通道和alpha通道中,有效提升了算法的压缩性能和嵌入容量,最终实现两幅明文图像的视觉安全加密。仿真结果和性能分析表明,本文所提算法具有良好的视觉安全性、压缩性能和较高的执行效率,可为资源约束环境下的多图像信息保护提供有效的解决方案。

1 混沌理论

1.1 Chebyshev混沌映射

Chebyshev映射是一种以阶数为控制参数的一维混沌映射[12],其数学迭代式为

xn+1=cos(karccos(xn))

(1)

式中:xn+1为状态变量,是该映射的迭代输出值;k为控制参数,其取值范围为[0,4]。图1给出了Chebyshev混沌映射的分岔图。从图中可以看出,该映射存在以下问题:①部分区域内存在不动点;②存在空白窗口;③在参数k的整个取值范围内,满映射状态分布不均匀。

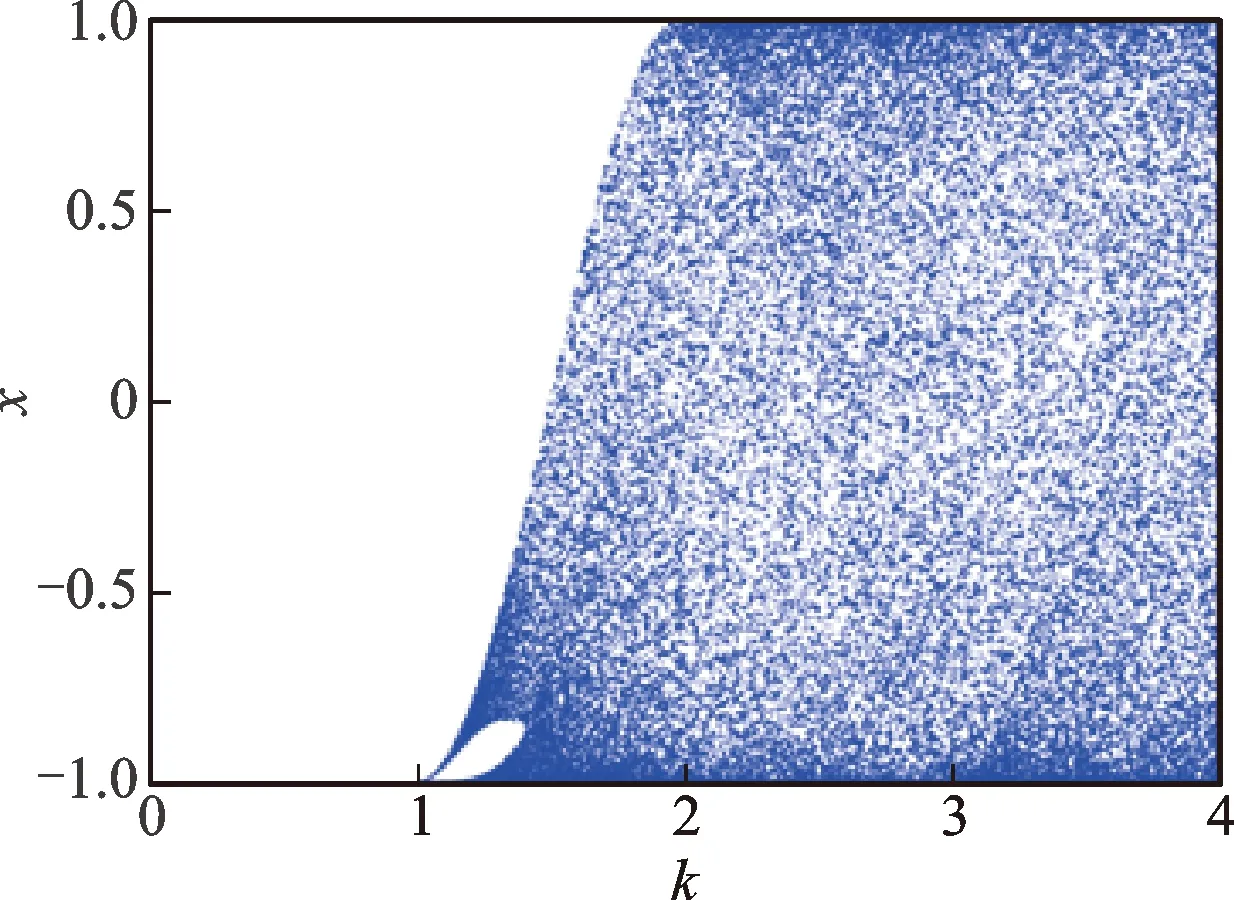
图1 Chebyshev混沌映射的分岔图Fig.1 The bifurcation diagram of Chebyshev chaotic map

1.2 改进型混沌映射

针对Chebyshev混沌映射存在的缺陷,本文对其系统方程进行改进,即在式(1)的基础上引入一个非线性项。改进的Chebyshev映射(improved Chebyshev map, ICM)系统方程

xn+1=cos(((4+u)π-usin(πxn))arccos(xn))

(2)

式中:u∈[0,4]为该改进型混沌映射的控制参数。

改进型Chebyshev混沌映射的分岔图如图2所示。由图2可见,在参数u的整个取值区间内,改进后的Chebyshev映射均处于满映射状态,同时不动点以及空白窗口等问题均得到解决。此外,在对应的硬件电路设计中,将Chebyshev混沌电路[13]中的控制项替换为带正弦函数的非线性电路,即可得到改进型Chebyshev混沌映射的电路。

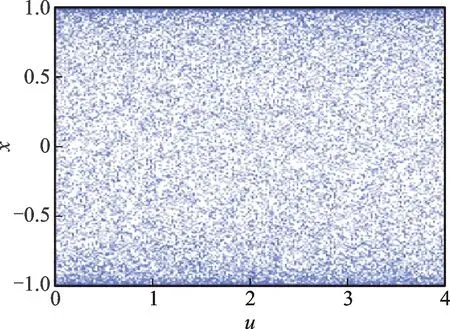
图2 改进型Chebyshev混沌映射的分岔图Fig.2 The bifurcation diagram of ICM map

1.3 改进型混沌映射的性能分析

1.3.1 李雅普诺夫指数

对于一维混沌映射f(xn),其李雅普诺夫指数(Lyapunov exponent,LE)可由式(3)计算得到[14]。若一个非线性动力系统的LE值大于0,则该系统存在着混沌现象,表达式如下

(3)

将本文改进型Chebyshev混沌映射的李雅普诺夫指数与文献[15-17]所提一维混沌映射的李雅普诺夫指数进行对比,实验结果如图3所示。

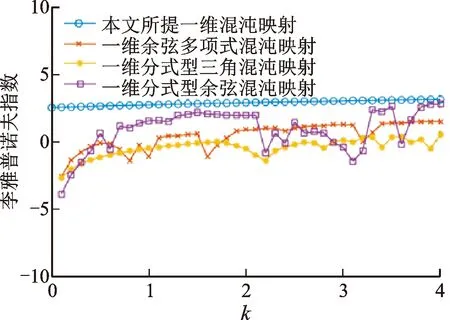
图3 一维混沌映射的李雅普诺夫指数谱Fig.3 Lyapunov exponent spectrum of 1D-chaotic map

可以看出,当控制参数u∈[0,4]时,改进型Chebyshev混沌映射的LE均大于0,说明该映射始终处于混沌状态。相比与其他的一维混沌映射具有更大的LE值,表现出更为复杂的混沌特性。

1.3.2 香农熵

香农熵(SE)表征的是非线性动力系统所产生的时间序列的混乱程度[18]。对于一维混沌映射而言,如果其产生的混沌序列越有序,则相应SE的值越低;反之,SE的值则越高。

对比本文改进型Chebyshev混沌映射和文献[15-17]所提出的一维混沌映射的香农熵,实验结果如图4所示。由图4可见,在整个区间上,改进的混沌映射的SE值均大于0,说明该映射所产生的混沌序列始终处于无序的状态。同时,与其他一维混沌映射相比,改进混沌映射的SE值波动的范围更小,表现出更为稳定的混乱程度。

图4 一维混沌映射的香农熵谱Fig.4 Shannon entropy spectrum of 1D-chaotic map

1.3.3 NIST SP800-22测试

本小节采用美国国家标准技术研究所发布的SP800-22测试套件[19-20]来对改进的混沌映射的伪随机性进行测试。假设显著性水平α=0.01,各子项测试的实验数据见表1。由表中数据可知,本文所提出的改进型Chebyshev混沌映射产生的混沌序列通过所有的随机性检验测试,说明其具有良好的伪随机特性。

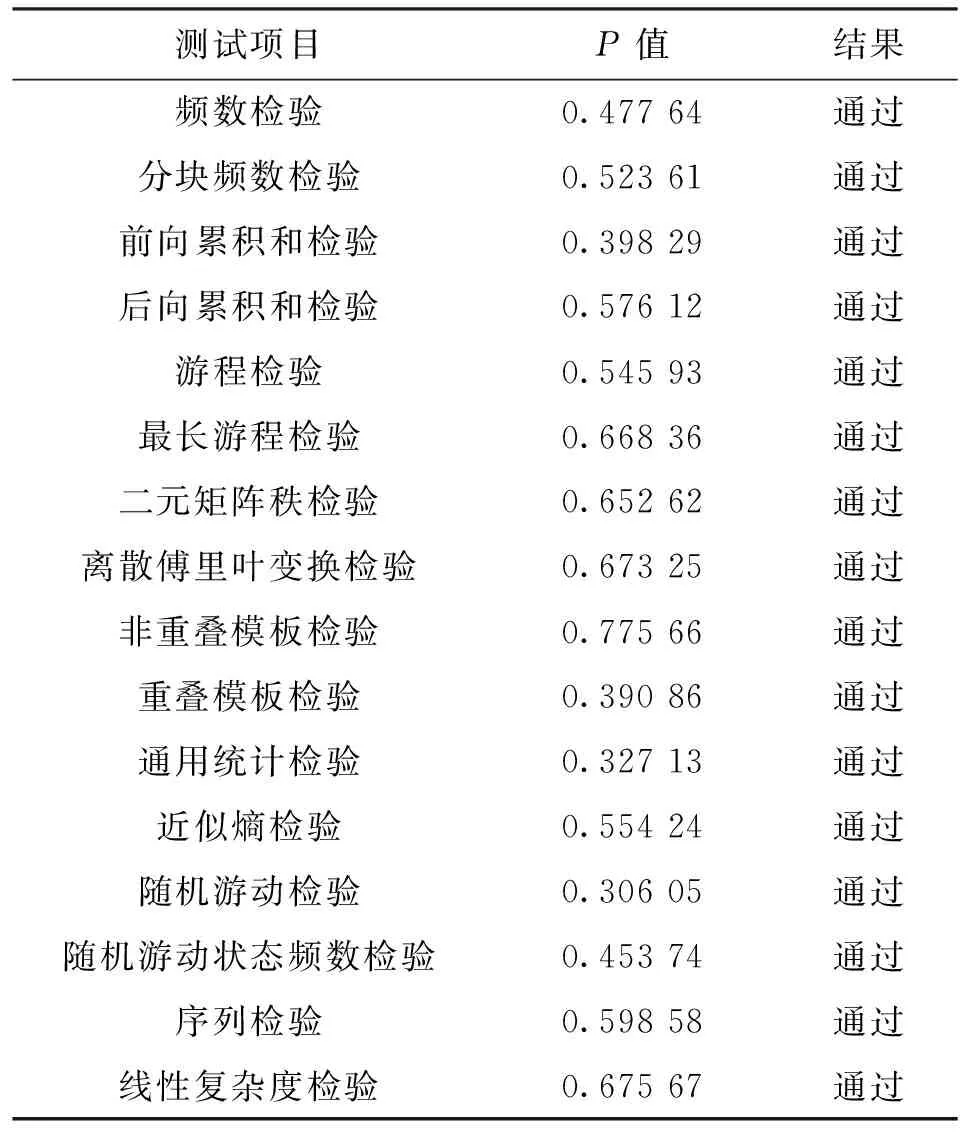
表1 NIST随机性测试的实验数据

2 双图像视觉安全加密算法

为在资源约束环境下实现多幅明文图像的视觉安全加密,有效提升算法的安全性、压缩性能、嵌入容量和执行效率,本文结合了改进型Chebyshev混沌映射和二维压缩感知技术,并利用图像的像素值通道和alpha通道同步嵌入多源的秘密信息,提出了一种高效的双图像视觉安全加密算法。主要包括压缩、二次加密和嵌入3个过程,对应的加密流程如图5所示。

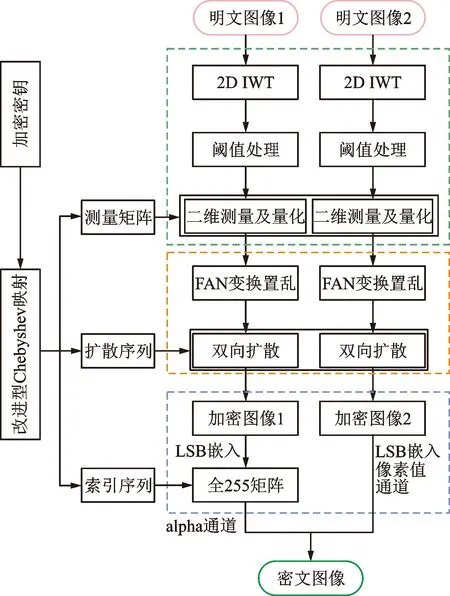
图5 加密算法的流程图Fig.5 Flow chart of proposed encryption algorithm

首先,通过两个受控测量矩阵对两幅明文图像的小波系数进行二维测量,完成图像压缩和初次加密。其次,考虑到压缩感知框架的线性测量特性不能抵抗选择明文攻击[21],再利用FAN变换和双向扩散对压缩图像进行二次加密,得到具有噪声形态的秘密图像。最后,利用最低有效位嵌入算法将秘密图像信息分别嵌入到载体图像的像素值通道和alpha通道中,以生成具有视觉意义的密文图像。此外,鉴于该嵌入算法不会导致嵌入过程中秘密图像的信息损失[10],因此载体图像可以任意选择。假设两幅明文图像为P1∈NN×N和P2∈NN×N,载体图像为C1∈NN×N。

2.1 二维压缩

步骤1分别对两幅明文图像P1、P2进行二维整数小波分解,得到它们对应的稀疏系数矩阵P3、P4,然后再对其进行阈值处理,相应的数学表达式为

(4)

式中:abs(·)表示绝对值函数;T1与T2分别为预设的阈值。经过阈值处理后所得到的系数矩阵命名为P5和P6。

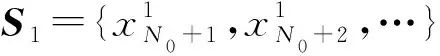
步骤3分别对混沌序列S1和S2进行抽样,从而得到两条抽样序列S3和S4。

(5)

式中:mod(·)表示取余数操作。

步骤4根据式(6)构建测量矩阵Φ1,测量矩阵Φ2同理可得。

(6)

步骤5对经过阈值处理后的系数矩阵进行二维压缩测量,其相应的数学公式如下

(7)

步骤6将测量后的实数矩阵P7和P8进行量化,获得两幅压缩图像。

(8)

式中:round(·)表示四舍五入操作;min和max分别代表取矩阵中的最小值和最大值。

2.2 二次加密

步骤1对压缩图像P9和P10进行FAN变换置乱,其中置乱过程的数学表述可由式(9)表示。

(9)

q=max[|t00|,|t01|,|t10|,|t11|]

(10)

式中:(in-1,jn-1)和(in,jn)分别表示置乱前后像素点的坐标。另外还须满足等式|t00t11-t01t10|=1。将经过FAN置乱后所得到的矩阵命名为P11和P12。

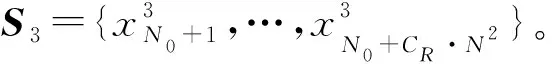
步骤3根据式(11)计算得到用于双向扩散操作的扩散序列D。

D=mod(S3+q0)×1010,256

(11)

步骤4对矩阵P11和P12进行双向扩散,以获得加密矩阵E3和E4。其中,式(12)(13)分别为前向扩散和后向扩散;n=1,2,…,0.5CRN2。

(12)

(13)

2.3 嵌入

步骤1为防止嵌入过程中可能发生的数据溢出,对载体图像的像素值进行缩放。

(14)

式中:A=10,μ=245。

步骤3按升序顺序对混沌序列S4进行排序,以生成索引序列T。

步骤4构造元素值均为255的4个方矩阵Wn∈N0.5N×0.5N(n=1,2,3,4),再将载体图像C2的像素值矩阵进行4等分分割以获得矩阵Un∈N0.5N×0.5N,(n=1,2,3,4)。

步骤5然后通过最低有效位嵌入算法将E3和E4分别随机地嵌入到矩阵Wn和Un中。

(15)

(16)

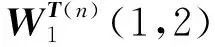
步骤6最后再将组合后的矩阵W作为alpha通道与组合后的矩阵U一起生成具有视觉意义的密文图像Q。

3 解密算法

解密方可根据密钥生成的密码流和受控测量矩阵对密文图像Q分别进行提取、解密及重建等逆操作,从而获得两幅解密图像,具体步骤如下。

(1)根据接收到的密钥值迭代ICM混沌映射以产生索引序列T、双向扩散序列D以及受控测量矩阵Φ1和Φ2。

(2)利用索引序列T和最低有效位提取算法从密文图像Q的像素值通道和alpha通道中提取出加密数据E3和E4。

(3)通过式(17)(18)从加密数据中求解出置乱后的矩阵P11和P12。

(17)

(18)

(4)对由从FAN变换逆置乱中得到的矩阵P9和P10进行逆量化操作。

(5)通过2DPG-ED重建算法[22]从压缩矩阵P7,P8中恢复出稀疏系数矩阵P5和P6。

(6)对系数矩阵P5和P6进行二维整数小波逆变换即可得到两幅解密图像。

4 算法性能分析

4.1 仿真结果

本节的性能测试均在装有Matlab 2018b的笔记本电脑上运行。加密密钥和其他参数设置如下:[u0,u1,u2,u3]=[3.799,3.987,1.293,2.471],[x0,x1,x2,x3]=[0.759,0.381,-0.652,0.385],[t00,t01,t10,t11]=[9,5,11,6],T1=30,T2=2,d=25,CR=0.5,B0=20,B1=107。

为了检验本文提出的双图像视觉安全加密算法的视觉安全性和压缩性能,本小节对其进行仿真实验,结果如图6所示。

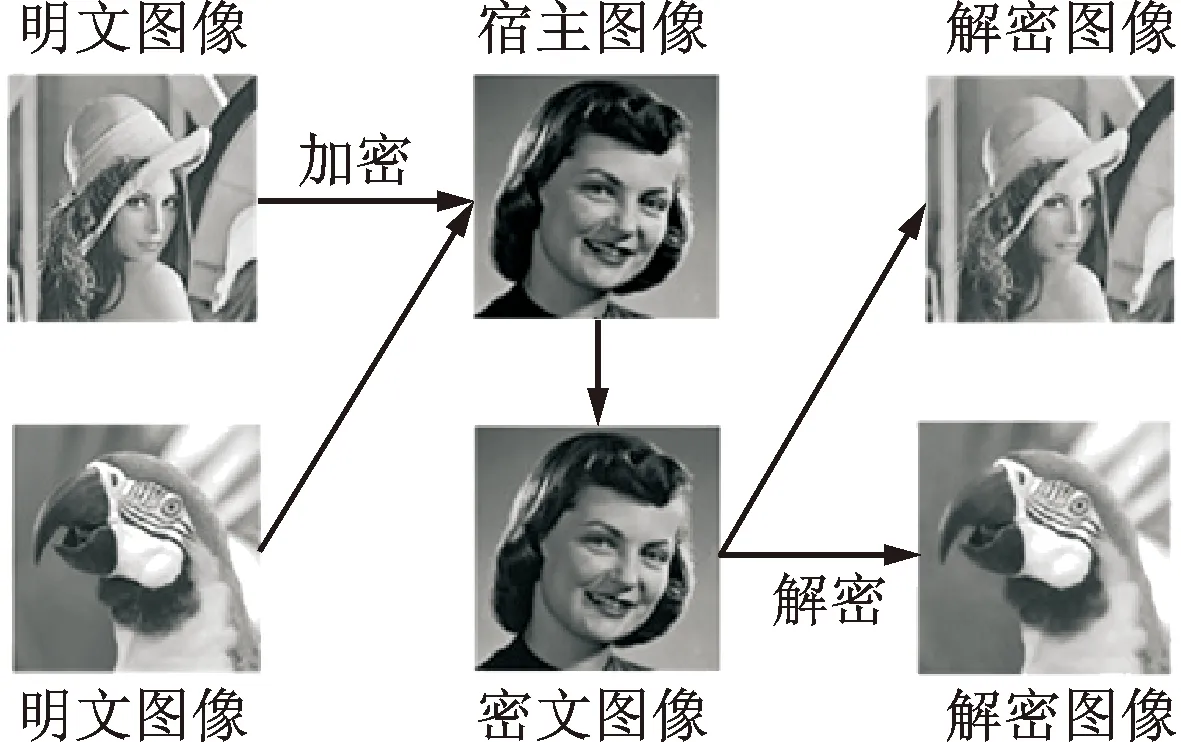
图6 所提算法对图像Lena和Parrots的加解密结果Fig.6 The encryption and decryption results of proposed algorithm on images “Lena” and “Parrots”

可以看出,经过压缩-加密操作的明文图像被成功嵌入到载体图像中,加密得到的密文图像与载体图像之间无显著视觉差异。因此本文所提的加密算法可以有效保证密文图像的视觉安全性。同时解密图像可以较为清晰的显示明文图像的绝大部分信息。为定量表示本文加密算法的视觉安全性和压缩性能,分别计算出密文图像与相应载体图像之间,以及解密图像和明文图像之间的峰值信噪比(peak signal to noise ratio,PSNR)[23]。前者为43.45 dB,后者为33.46 dB和37.19 dB。定性和定量实验结果表明,本文双图像视觉安全加密算法具有良好的视觉安全性和压缩性能。

4.2 性能提升分析

在本文所提出的加密算法中,可通过设置阈值使得明文的小波系数更加稀疏从而进一步提升压缩性能。本文选用Lena和Parrots作为明文图像,Girlface作为载体体图像,考察阈值对仿真实验结果的影响,如图7所示。可以看出:①阈值对解密图像质量的影响并不是单一的,当阈值的取值小于最优阈值时,随着阈值取值的增大,解密图像的质量也随之增大,反之,则随着阈值的增大而减小;②阈值对密文图像不可见性的影响可以忽略。基于此,文中的阈值设置分别为T1=30和T2=2。

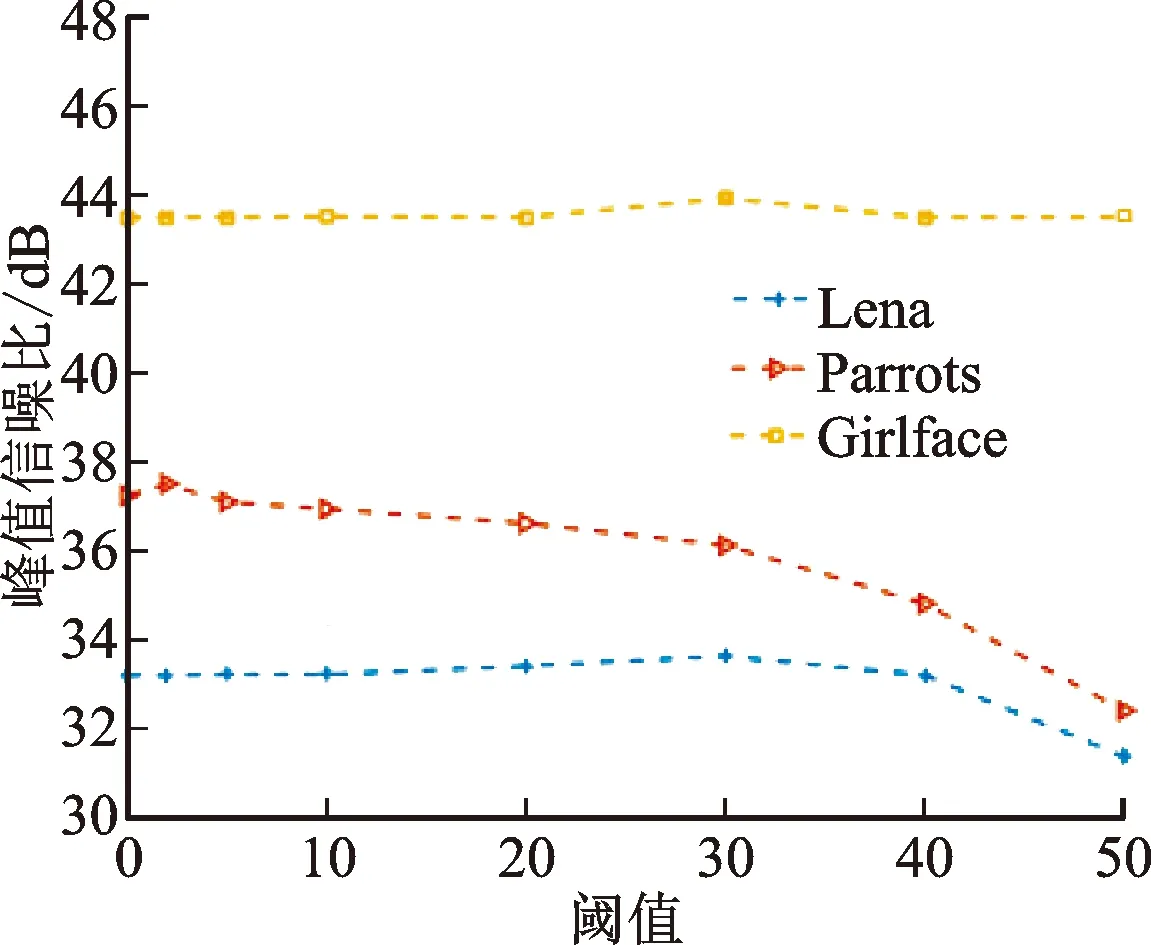
图7 阈值对仿真结果的影响Fig.7 The impacts of thresholds T1T2 on simulation results

混沌映射对于受控测量矩阵的有限等距性质和算法的压缩性能均有一定的影响。图8为Cheb-yshev混沌映射和其改进型对于压缩性能影响的走势图。从图8可见,在整个参数取值范围内,利用改进型混沌映射得到解密图像的视觉质量更高且变化范围更小。因此,算法的压缩性能在提升的同时更趋于稳定。

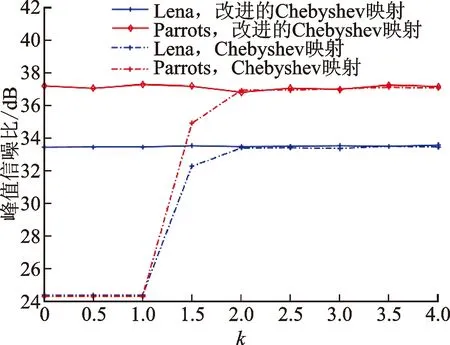
图8 混沌映射对压缩性能的影响Fig.8 The impacts of chaotic map on compressive property

4.3 安全性分析

4.3.1 密钥分析

密钥空间以及密钥敏感度可表明加密算法抵抗暴力攻击的能力。本文算法的密钥主要由混沌映射的控制参数[u0,u1,u2,u3]与初始状态[x0,x1,x2,x3]组成。假设双精度数据的计算精度为10-14,则本文总的密钥空间为(1014)4×4×(1014)2×4=10336。同时,由表2给出的比较结果可见,本文提出的加密算法具有更大的密钥空间。

表2 不同加密算法中密钥空间的对比结果

对明文图像Lena和Parrots进行二维压缩、加密后随机地嵌入到载体图像Girlface中。分别对某一解密密钥添加一个极小的扰动,并保持其余相关密钥不变。最后使用八组错误的密钥对密文图像进行解密,结果如图9所示。

(a)u0+10-14 (b)u1+10-14 (c)u2+10-14

由图9可以看出,解密密钥的微小变化都会导致解密图像与其对应的明文图像之间存在巨大差异,无法从中提取任何有视觉意义的信息。通过上述分析,本文提出的加密算法具有较大的密钥空间和强的密钥敏感性,足以抵抗暴力攻击。

4.3.2 直方图分析

为抵抗统计攻击,一个有效的加密算法所得到的秘密图像应具有均匀的直方图分布。本小节采用分辨率为512×512像素的明文图像Peppers、Zelda和载体图像Baboon进行测试。实验结果如图10所示。可以看出,本文中加密算法生成的秘密图像的像素值趋于均匀分布。在另一方面,密文图像与载体图像的直方图高度近似,表明嵌入算法可有效保留载体图像大部分的像素值分布。

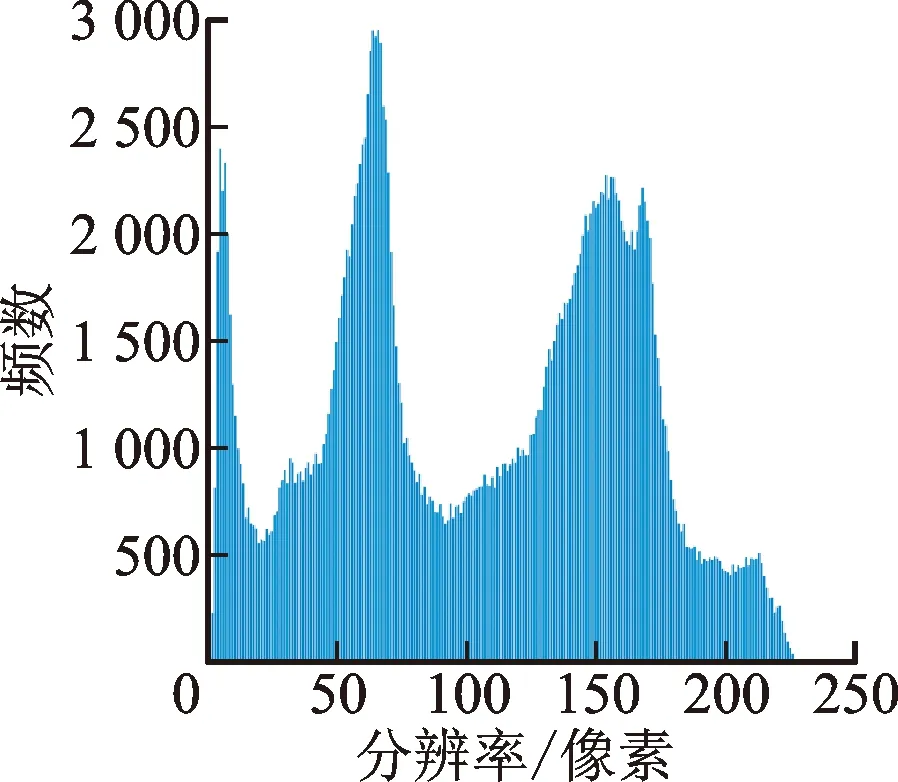
(a)明文图像Peppers

4.3.3 抗差分攻击分析

本文设计的加密算法所产生的密文图像具有视觉安全特性,因此明文图像的微小变化主要体现在秘密图像的差异上。假设I1和I2是两幅仅有一个比特位差异的明文图像,则其相应的抗差分攻击性能指标可以由像素变化率(INPCR)和归一化平均变化强度(IUACI)[26]计算得到。表3为加密算法在抵抗差分攻击方面的实验结果。从表中可知,本文中的密文图像的INPCR和IUACI值接近于理论值99.609 4%和33.463 5%[24],即明文图像的细微变化将会导致密文图像产生显著差异,这意味着加密算法对差分攻击具有很强的抵抗能力。

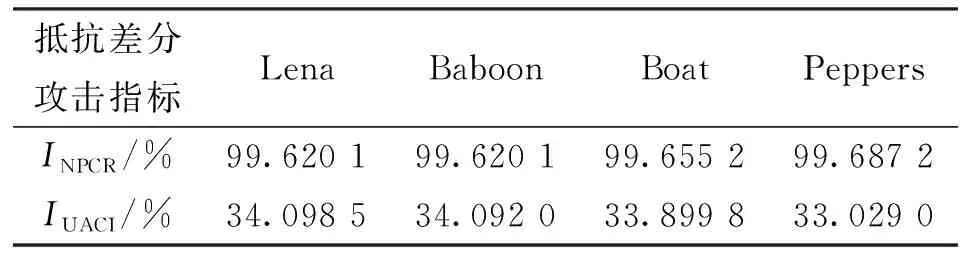
表3 本文加密算法对4种明文图像抵抗差分攻击的实验结果

4.3.4 视觉安全性分析

对于视觉安全加密算法而言,密文图像与载体图像的相似度越高,算法的视觉安全性也越强。本小节将采用峰值信噪比和平均结构相似度(mean structural similarity,MSSIM)[23]来定量评估载体图像和密文图像之间的相似度。应用本文和文献[24-25]中的加密算法分别对4幅512×512像素的明文图像进行加密(其中,本文算法同时加密两幅相同的明文图像),并计算密文图像与对应载体图像之间的PSNR和MSSIM的值,实验结果如表4所示。表中数据显示,与文献[24-25]相比,本文提出的加密算法在嵌入容量提升一倍的情况下,所生成的密文图像依然具有较好的视觉安全性。

表4 视觉安全性分析的实验结果

4.4 压缩性能分析

考虑到本文加密算法采用了有损压缩及线性量化操作,为此对多幅512×512像素的明文图像进行仿真实验,以定量评估加密算法的压缩性能。仿真测试所得到的实验数据如表5所示。此外,对比文献[24-25]的实验数据,可以看出本文提出的双图像视觉安全加密算法具有良好的压缩性能。这得益于所采用的完全可逆的嵌入和提取算法,而导致文献[24-25]压缩性能损失的因素不仅包括因量化操作而带来的截断误差,同时还有嵌入操作而带来的能量损失。

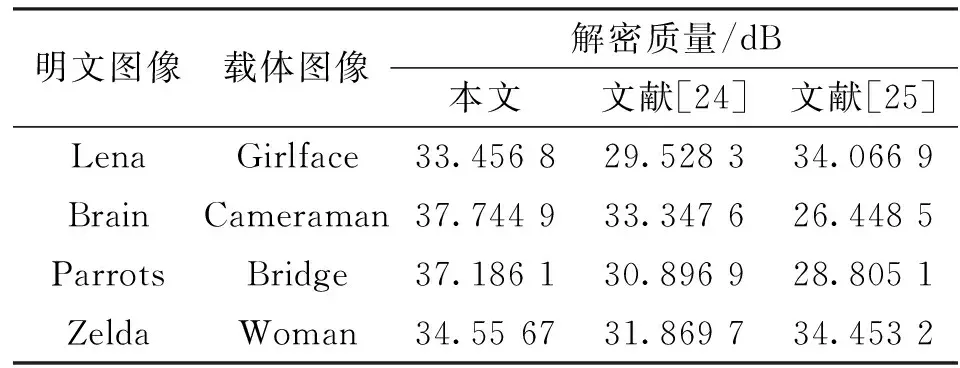
表5 解密质量分析的实验结果

4.5 鲁棒性分析

在信道中传输时,密文数据有可能会受到噪声的污染,为了定性评估本文算法抵抗噪声攻击的能力,对密文图像分别添加不同强度的椒盐噪声(ISPN)和斑点噪声(ISN),实验结果如图11所示(明文图像Lena和Parrots分别加密并嵌入到载体图像的像素值通道和alpha通道中)。可以看出,本文所提出的双图像视觉安全加密算法具有一定的抗噪声干扰的能力。相比于椒盐噪声,斑点噪声对加密算法的影响更大。另外,随着噪声强度的增加,从

(a)ISPN=0.001%

alpha通道中提取出并解密得到的图像的视觉质量衰减的更快。

4.6 加密用时分析

本文所提双图像加密算法的时间开销主要由压缩、二次加密及嵌入用时构成。其中,二维压缩环节的时间复杂度为O(dCRN2);二次加密中,FAN变换置乱和双向扩散的时间复杂度为O(6+CR)N2),嵌入部分对应的时间复杂度为O(0.75N2)。因此本文算法总的时间复杂度为O((6+CR)N2)。

为定量评价本文算法的时间效率,表6给出了不同算法处理512×512像素明文图像所需时间的对比结果。可以看出,相比文献[8]、文献[24]中采用的三维和四维混沌系统,本文算法的加密用时分别减少42%和75%。同时,在秘密信息嵌入容量扩大一倍的情况下,嵌入用时相比文献[8]也减少了49%。最短的总用时表明本文算法具有较高的时间效率。

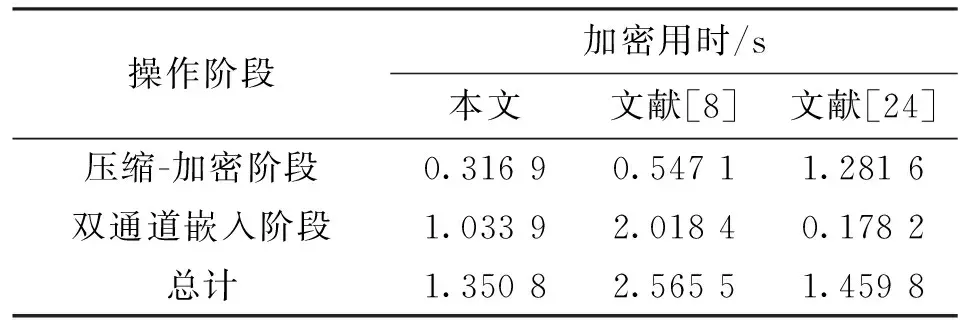
表6 加密用时对比的实验结果

5 结 论

针对资源约束环境下的图像信息保护问题,本文从加密算法的安全性、压缩性能和执行效率入手,利用改进的混沌映射和二维压缩感知提出了一种高效的双图像视觉安全加密算法。与现有的单图像视觉安全加密算法相比,在加密效率、压缩性能和嵌入容量方面均有不同程度的提升。

(1)对经典的一维Chebyshev混沌映射进行改进,进一步提升了其混沌特性,在保证算法的安全性的同时,加密用时减少了40%以上,加密效率明显提升。

(2)利用二维压缩感知技术对明文图像进行压缩,并结合改进混沌映射所构建的测量矩阵和阈值设置,可获得约1～7 dB的压缩性能增益。

(3)在载体图像像素值通道和alpha通道中同步嵌入两幅明文图像的秘密信息,嵌入容量扩大了一倍,同时密文图像的视觉安全性没有发生退化。

综上,本文所提出的算法具有良好的安全性、压缩性能和较高的执行效率,可在资源约束环境下实现两幅图像的同步压缩和视觉安全加密。