基于脉冲位置调制的激光雷达距离速度测量方法

黄少伟,周亚琪,雷闰龙,毛雪松

(1.肇庆学院计算机科学与软件学院/大数据学院,广东 肇庆 526061；2.武汉科技大学信息科学与工程学院/人工智能学院,湖北 武汉 430081)

1 引 言

市场上销售的应用于智能驾驶实验车的激光雷达根据测量激光的飞行时间获得障碍物的距离,具有较高的测量精度。另一方面,在智能驾驶应用中,根据多次测量目标距离,通过计算距离的平均变化率可以获得运动目标的相对速度[1-2]。然而,这种速度测量方法所需耗费的时间较长、所测得的速度误差较大,不能满足智能驾驶高速运动规划的需求。用多普勒的方法测得的速度相比于求距离变化率的方式得到的目标速度在精度上要高两个数量级,且所需的时间短[3-5],但脉冲式多普勒激光雷达的距离分辨率很差,不能满足智能驾驶的需求。在智能驾驶应用中,期望激光雷达能够在测量目标距离的同时,利用多普勒测量目标的速度。但是,到目前为止,很少有相关研究来解决这一问题。利用多普勒同时测距测速的典型方法为毫米波雷达常用的三角啁啾频率调制连续波(Frequency Modulated Continuous Wave,FMCW)[6-8],基于FMCW方式开发的激光雷达,能够同时高精度测量目标的距离和速度[9-10]。但是这种方式为完成一次测量所发射的信号长度达到几毫秒。为提高空间分辨率,汽车激光雷达要求1 s内能够完成几万到数十万次测量,因此这种方式不能满足激光雷达的高速扫描要求。另一方面,这种方式发射连续波,峰值功率通常只有几毫瓦[11-12]。由于道路环境中存在大量低反射率目标,例如穿黑色衣服的行人,因此存在近距离目标的回波功率低于激光检测器的量子极限,增加了检测器设计难度甚至无法检测。高爽在文章[13-14]中提出一种复合光场的频率调制连续波方法,其信号长度满足智能驾驶扫描的需求,距离和速度的测量精度也很高,但这种方式发射连续波,在检测方面存在与经典FMCW方式同样的问题。特别地,这种方式将距离测量信号和速度测量信号复合在一起,接收端再将其分离分别用于测量距离和速度,实质上就是将两个激光雷达装置组合成为一个装置,增大了对环境的光辐射。另外,根据毫米波雷达使用的经验,连续波方式存在较多的干扰问题,当应用于城市道路环境中时,干扰问题将不可避免。

为解决连续波方式存在的固有缺陷问题,课题组提出使用伪随机脉冲序列调制发射光幅度[15-16]的方式,实现汽车激光雷达同时测量目标的距离和速度,并通过计算机仿真验证了这些方法的正确性。但是,伪随机脉冲序列属于一种准连续波,为保证发射信号平均功率在安全标准范围内,所允许的发射峰值功率同样不能太大。为提高发射信号的峰值功率,解决激光检测的量子极限问题,必须减少脉冲序列中脉冲的个数。文献[17]～[19]提出了在激光雷达中使用脉冲位置调制方式,用于减小接收机的体积,实现了距离测量的功能,并比较了该方式的抗干扰性能,但未提及同时测量速度的问题。

本文在文献[17]的基础上,进一步提出利用非等间隔傅里叶频谱分析方法,解决基于脉冲位置调制波形的距离和速度同时测量问题。针对脉冲在时间轴上位置的随机分配,设计两种方案并对比测量性能的优劣。在抗干扰性能方面,利用两组功率、延时变化不同的回波构成复合波形来模拟受干扰的信号,并对复合波形做信号处理,从距离和速度两个方面分别进行评价测量的准确性。

2 激光雷达的接收系统模型

图1给出实现距离和速度同时测量的激光雷达系统框图,激光器输出连续光通过分光器分为两路,其中一路经调制器调制为脉冲位置调制序列,再由光放大器放大后经发射透镜准直透射到激光雷达的扫描装置上；另一路用作本地参考信号,被发送到合波器。来自目标的回波信号经透镜汇聚后耦合到光纤,经分光器分为两路,其中一路直接发送到光电转换器PD1用于测量目标的距离,另一路发送到合波器,在合波器内与本地参考信号耦合后发送到光电转换器PD2,由PD2输出回波信号与本地参考信号之间的差频信号,该差频信号的频率即为多普勒信号的频率,对应于运动目标的速度。

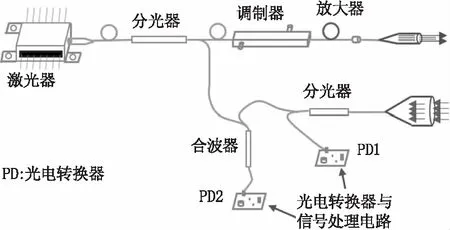
图1 激光雷达的系统框图

在速度测量中,为了能够获得多普勒频率,使用了差频的方法,因此要求激光器的输出为偏振光信号,系统中所使用的光纤均为保偏光纤。为了保证速度测量的精度,要求光具有一定的相干度,因此激光器输出光的线宽一般选择为不高于30 kHz。为了保证脉冲序列中相邻脉冲之间的相干性,不使用对激光器通断电的直接调制方式,而是使用光外部调制器对激光器输出的连续光做幅度调制。经调制器输出的光脉冲序列的峰值功率只有几毫瓦,需经过放大器放大后才能作为测量信号发射到扫描装置。

用于智能驾驶的激光雷达中,光的传输均采用自由空间耦合的方式,图1激光雷达系统内光的传输选用光纤耦合,一方面因为自由空间耦合的电信号处理单元与整个装置集成并安装于车外,工作环境恶劣,电子器件的工作稳定性差,而用光纤耦合可以将电信号处理单元安装于驾驶室内,解决了电子器件的工作环境的问题；另一方面,为提高距离分辨率,脉冲序列中单个脉冲的宽度为几纳秒,自由空间光调制器的调制速度不能满足要求,例如Thorlab在线产品中,自由空间光调制器的最大调制速度为200 MHz,而使用光纤耦合的高速电光调制器的速度可以达到几十吉赫兹。本文假设脉冲序列中单个脉冲的宽度为1 ns,对应调制器的调制速率为1 GHz。

单个脉冲可表示为:

(1)

式中,A表示脉冲的幅度。则随机脉冲序列表示为:

(2)

其中,N为脉冲序列中脉冲的个数;ri表示脉冲的随机位置。

PD1的输出为幅度衰减的脉冲序列:

(3)

其中,τ为目标距离引起的延时因子；α为包含反射、散射、大气衰减等各种因素在内的总的衰减因子。照射到PD2光敏面的光信号为:

cos[2π(f0+fD)t+φr]

(4)

式(4)右边第一项为本地连续光参考信号,第二项为来自目标反射的回波信号。γ为本地参考信号的幅度,f0为光源的频率,fd为多普勒频率,φ0为初始相位,φr为包含延时的接收信号相位。光敏面对输入光的强度敏感,且滤除高频后得到差频信号为:

(5)

两个光电转换器的输出波形样本如图2所示。从图中可以清晰地看出,PD2输出的多普勒信号其轮廓为余弦振荡,但对该信号采样不能得到余弦信号的等间隔数据。

图2 激光雷达接收机输出波形

3 距离速度测量方法

本文提出脉冲位置调制方法实现汽车激光雷达同时测量目标的距离和速度,需要设计具体的调制格式以及PD1和PD2输出信号的处理方式。

3.1 两种脉冲位置调制格式

首先根据激光雷达单位时间内要求测量的空间点数,确定完成单次测量所分配的时间长度。设单位时间内测量的空间点数为M,则完成一次测量所需要的最大时间为1/M(s)。要求激光雷达能够测量的最大距离为d(m),激光的飞行时间为τ=2d(m)/c(m/s),c表示光速。因此,完成一次测量的脉冲序列长度最大为T=1/M-τ(s)。

如图3所示,构成位置调制的脉冲序列有两种方式,一种是在长度为T的时间内随机生成N个互不相等的位置,并将脉冲放置于相应的位置处,如图3(a)所示,这种序列方式的脉冲间隔差异很大。另一种方式为将长度为T的时间按照脉冲的个数N分为N个等时长的时隙,然后将每个时隙内随机位置处放置一个脉冲,如图3(b)所示。

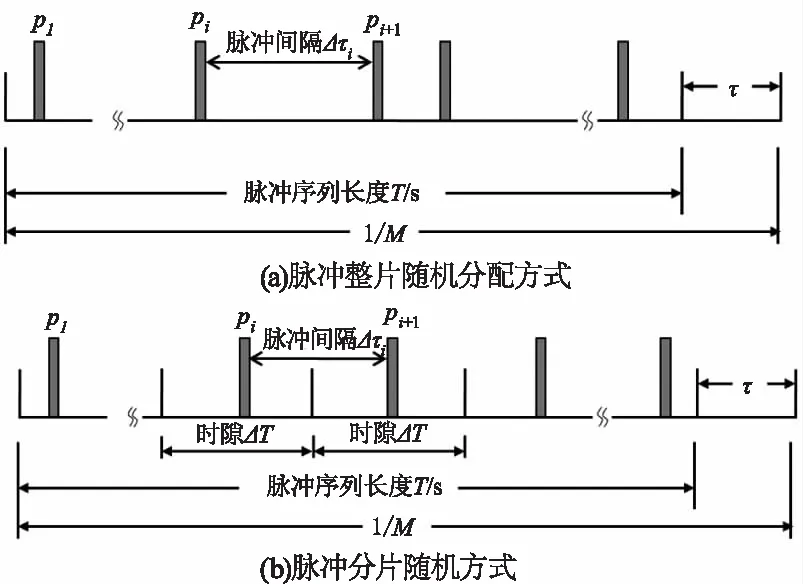
图3 位置调制脉冲序列的组成方式

3.2 用于距离测量的数据累加方法

使用随机脉冲序列作为测量信号,为确保激光雷达辐射功率在安全标准范围内,其峰值功率不可过大,因此一般情况下回波淹没在接收机的热噪声中。为了确定接收机输出信号中回波的位置,雷达信号处理中常用数据累加的方法。针对本文设计的雷达信号波形,改进传统的数据累加方法,其工作原理如图4所示。

图4 数据累加方法原理

发送端生成调制码时,保存相邻脉冲之间的间隔ΔT1、ΔT2,…。接收端从激光雷达发射脉冲序列的第一个脉冲开始,对接收机的输出采样,采样频率确保对每个脉冲都能获取一个数据,采样时长为1/M(s),将采样所得信号保存于一数组s(n)中,如图4的第一行所示,其中的时延对应于脉冲序列与测量目标之间的往返飞行时间(作为原理演示,图中画出时延的位置,实际上信号淹没于噪声中)。将数组s(n)中前ΔT1时间内的数据丢弃,并将后面的数据逐位左移得到新数组s(n+ΔT1),将该数组数据放于图4的第二行。再将第二行的数组s(n+ΔT1)左移得到s(n+ΔT1+ΔT2)放置于第三行,以此类推直到数组中剩下最后一个脉冲。最后将N行数组相加,在对应于时延的位置处,将出现一个大的峰值,而其他位置处仅有很小的波动,这些波动依然淹没在噪声中,对脉冲序列时延的检测不噪声干扰。

3.3 用于速度测量的频谱分析方法

等间隔采样离散信号的傅里叶变换定义为:

(6)

当对信号的采样间隔不相等时,相邻采样间隔记为ΔTi,(i=1,2,…),连续信号的傅里叶变换可以为成:

(7)

对比式(6)和式(7)可以看出,将f(ti)Δti作为离散傅里叶变换的时域数据,即可以在采样间隔不等的情况下得出连续信号f(t)的频谱。

4 仿真结果分析

为确保激光雷达的空间分辨率足够大,本文的仿真中规定平均每秒测量空间点数为20万个,因此单次测量所需的时间最大为5 μs。规定激光雷达的最大测量距离为150 m,则激光往返最远目标的飞行时间为1 μs。为确保脉冲序列中最后一个脉冲能够返回接收机,需要在最后一个脉冲发射后设置1 μs的等待时间,故脉冲序列的最大长度为4 μs。利用傅里叶变换分析信号频谱,时间窗口越大,则频域分辨率越高。为提高速度测量的精度,需要时间窗口越大越好,故在仿真中规定发射脉冲序列长度为4 μs。另一方面,距离分辨率与构成脉冲序列的单脉冲宽度有关,脉冲越短分辨率越高,在仿真中选择脉冲的宽度为1 ns,对应30 cm的距离分辨率。

4.1 两种调制格式的距离测量性能

距离的测量误差、分辨率仅与所选择脉冲的宽度、采样率有关,在两种调制格式的参数选择一致的情况下,应具有相同的性能。调制格式的不同主要影响的是接收信号的抗噪声性能,为公正比较两种调制方式,第一种方法将100个脉冲随机分配到长度为4 μs的时间段内,且不同脉冲不允许发生重叠,称为整片随机；第二种方法为,将4 μs分为100个时间片,每个时间片的随机位置处放置1个脉冲,称为分片随机。接收信号的信噪比低于5 dB后,信号均被淹没在噪声中,需要对两种调制方式分别使用第3.2小节的数据累加方法,确定脉冲序列相对于发射时刻的时延。为评价两种调制方式的距离测量的抗噪声能力,本文统计数据累加得到的信号峰值位置与实际时延不一致的概率。如果两者不一致,则表明距离测量发生了差错,将这一概率定义为检测错误概率。

两种调制方式的在不同信噪比情况下统计得到的测量错误概率如图5所示,横轴为信噪比,单位为分贝(dB),纵轴为错误概率的百分比。从图中可以看出,调制格式的不同对距离测量的性能影响几乎可以忽略。如果脉冲序列中含有100个脉冲,当信噪比大于-5 dB以后,检测的错误概率趋于零,而在信噪比低于5 dB后,检测错误概率迅速上升。

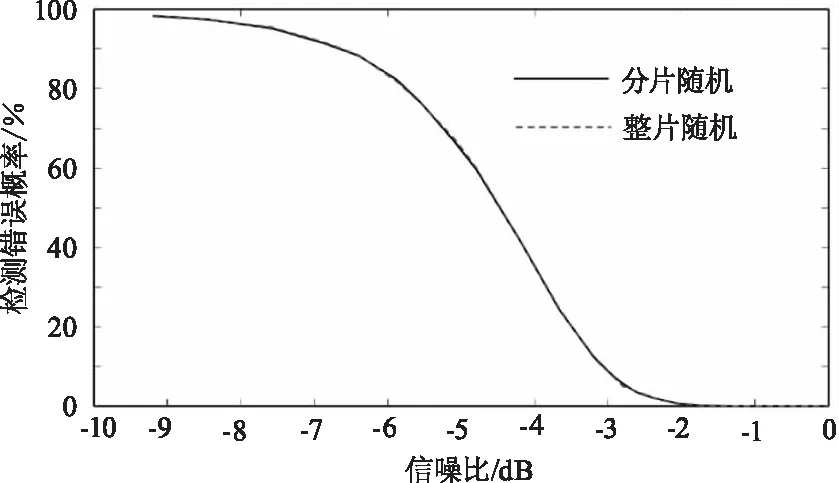
图5 两种调试方式的距离测量错误概率

4.2 两种调制格式的速度测量性能

设激光雷达的光源波长为1550 nm,对应1 m/s步行速度的多普勒频率为1.29 MHz,两车相对行驶相对最高速度360 km/h对应的多普勒频率为129 MHz。根据距离测量结果和PD1与PD2之间的固定时延确定回波信号的位置,然后根据式(7)调整信号的幅度,最后利用快速傅里叶变换(Fast Fourier Transform,FFT)对两种调制方式在不同信噪比下统计速度错误测量的概率。考虑到傅里叶变换本身存在的误差,当计算得到的信号频率与实际频率之间差值大于100 kHz时,认为测量将噪声峰值视为多普勒频率。对频率为1.29 MHz、5 MHz、20 MHz、40 MHz、80 MHz、129 MHz的信号在不同信噪比处计算10万次信号频率统计出错概率,结果如图6所示。观察结果表明,多普勒频率的不同对正确测量概率没有影响,因此图6中只给出了频率1.29 MHz情况下的两种调制方式统计结果。

可以看出速度测量对信噪比的要求低于距离测量约5 dB,因此接收端的分光器可以选择90∶10类型,将大部分光功率分配到距离检测装置。从图6还可以看出,图3(b)的分片随机调制方式在速度测量方面的性能要优于图3(a)的整片随机调制方式。综合考虑距离测量和速度测量的结果,本文建议在激光雷达波形调制的设计中,使用图3(b)的分片调制方法。

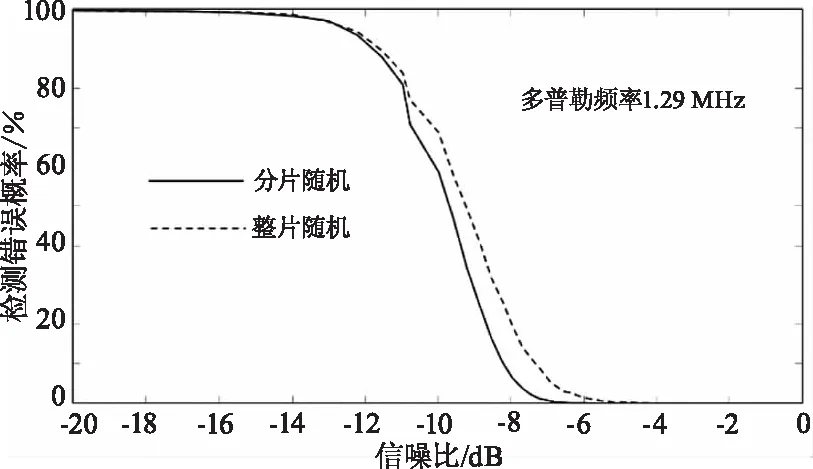
图6 噪声引起的两种调制方式速度测量错误概率

FFT对信号频率的计算本身存在误差。采用FFT计算不等间隔数据的频率,在1 MHz到129 MHz频率范围内统计误差,结果表明频率误差在一定范围内周期波动,与等间隔数据的FFT结果类似。图7给出了1 MHz到5 MHz统计的误差结果,其他频率范围的结果与该频率范围的结果一致。统计表明该误差与信噪比无关,仅与信号的当前频率有关。时间窗口为4 μs、数据点100个的情况下得到的最大频率误差为66.67 kHz,对应的速度测量误差为0.052 m/s,测量所耗费的时间长度为5 μs(不考虑计算时间),符合智能驾驶对动态场景信息获取精度的要求。

图7 正确测量时的频率误差范围

4.3 干扰对距离和速度测量的影响

激光雷达的波束很窄,可以不考虑测量信号的波束内出现两个反射目标的情况,即回波与干扰不同源。在城市道路环境中,车辆较多,存在一定的空间干扰概率,有必要分析相邻激光雷达对本机的干扰。干扰可以来源于周围激光雷达的直射型干扰或者反射型干扰,这两种干扰本质上具有一致性,只是到达本机的干扰强度有很大区别。由于干扰与测量信号不同源,它们的脉冲间隔具有很大的随机性,可以利用这一随机性来消除干扰。为研究干扰对正常回波信号的影响,本节中忽略接收机的噪声。另外,由于分片随机调制方式的测速性能较好,这里只分析这种调制方式的抗干扰性能。

设回波和干扰分别为:

(8)

(9)

将式(8)和式(9)中的αR、αI、TR和TI取不同的值并相加,得到的复合信号可模拟回波受干扰影响的情形。改变αR和αI的相对幅度,可以模拟干扰的程度。接收端已知回波的脉冲间隔,因此在数据累加过程中按照脉冲间隔移位。对于反射型干扰,干扰的幅度和回波的幅度相差一般在10倍以内,且通常为回波幅度大于干扰幅度。当回波幅度和干扰幅度相等时,数据累加得到的结果如图8所示,结果中只有一个峰值对应于回波的时延,反射型干扰的影响被消除。

图8 弱干扰对回波的影响

大气对激光的衰减相对于反射引起的激光功率损耗几乎可以忽略,因此如果发生对面车辆前置激光雷达或前车尾部激光雷达的发射信号未经反射而直接进入本地激光雷达的接收机,则干扰的幅度会远远大于回波的幅度。数据累加仿真结果表明,当干扰强度为回波强度的10倍时,仍然可以从干扰中将回波识别出来。数据累加的结果如图9所示,旁瓣幅值明显增加,对主峰的判断造成影响。

在PD2输出的外差信号中,若混入了干扰信号,干扰信号对应的多普勒频率不同于回波的多普勒频率。设PD2输出信号中回波和干扰分别为:

(10)

(11)

其中,αoR和αoI分别表示回波和干扰的幅度；To1和To2分别表示相对于发射起始时刻回波和干扰的时延；fDR和fDI分别表示回波和干扰的多普勒频率；φr和φI分别表示回波与干扰的相位。

图9 强干扰对回波的影响

在干扰的幅度与回波幅度相等的情况下,将式(10)和式(11)表示的回波与干扰叠加,并采用非等间隔傅里叶频谱方法计算得到的频谱如图10所示。在两个多普勒信号都被等间隔采样的情况下,频谱中应存在两个峰值分别对应回波与干扰的多普勒频率,在非等间隔采样的情况下,由于只对回波根据式(10)做了正确的幅度调整,因此频谱中只出现了一个对应于回波的多普勒频率,干扰的多普勒频率不会出现,因而可以消除干扰的影响。

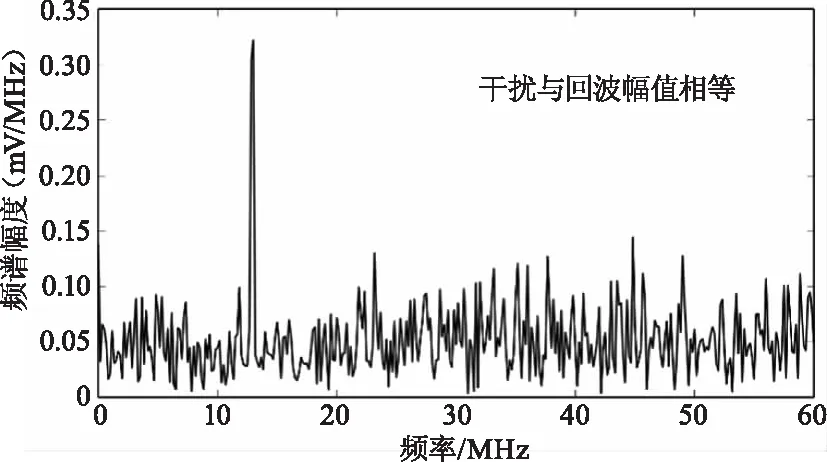
图10 干扰与回波同时存在时得到的频率,干扰的频谱不出现

随着干扰的增强,无论距离还是速度,测量结果都会受到严重的影响。图11给出了干扰与回波在不同幅度情况下距离和速度测量出现错误的概率。横轴的干扰回波比定义为:

(8)

式中,AI和AS分别表示干扰和回波的幅度。纵轴表示测量中将干扰误测量为回波的百分比概率。距离测量中,数据累加的峰值受干扰影响会以一定概率出现在非回波时延位置,但该位置与干扰的时延无关。同样地,速度测量中,会以一定概率出现干扰的频谱峰值大于回波频谱峰值,其峰值也不对应于干扰的多普勒频率。

图11 干扰对距离和速度测量的影响

从图中可以看出,相比于噪声,干扰对回波的影响要小得多,这是因为干扰仅存在与有限的时间点处,而噪声在整个连续时间上都存在,在相同峰值功率的情况下噪声的能量更大。另外,还可以看出和噪声相似,干扰对多普勒频率计算的影响比数据累加的影响小,第4.2小节中得出的将更多回波功率地分配给PD1用于距离计算这一结论在考虑干扰的情况下依然成立。

5 结 语

目前应用于智能驾驶实验车的激光雷达只能测量目标的距离,而不能测量目标的速度,在动态场景的路径规划等任务中存在困难。本文提出一种基于脉冲位置调制的激光雷达波形调制方式,并设计数据累加和非等间隔数据的频谱分析方法,从理论上实现了激光雷达的距离和速度同时测量。比较了两种位置随机调制格式的性能,得出位置分片随机在速度测量方面具有更好的抗噪声性能。最后,通过仿真分析了位置分片随机调制方式的抗干扰性能,得出可允许的干扰强度范围。结果表明,所提出的脉冲位置调制方法可以应用于道路环境中目标距离和速度的测量。