线性EIV模型参数的LASSO估计方法
赵明清,席甜甜
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
针对线性EIV模型参数的最优估计问题,国内外学者对其进行了广泛而深入的研究,先后提出了整体最小二乘(TLS)法和加权整体最小二乘(WTLS)法,并在此基础上进行了拓展性研究[1-10]。但以上研究只考虑了模型的拟合优度,而忽略了其复杂度,这易导致过拟合现象,并因此会降低模型的泛化能力。为此,王乐洋等[11]在WTLS的基础上添加参数向量的2-范数惩罚项,并做某种近似处理后得到了参数估计的解析解;Zhu等[12]在LS的基础上添加随机误差矩阵的F-范数和参数向量的1-范数惩罚项,将单层优化问题转化为双层优化问题进行求解,给出了具体的参数估计数值解算法,并在WTLS的基础上添加参数向量的1-范数惩罚项,采用类似的技巧进行了讨论,但没有给出其具体求解算法。本文基于结构风险最小化原则,提出线性EIV模型参数的LASSO估计(LE)方法,通过运用该方法对2001—2017年我国个人卫生支出占比影响因素的实证,与WTLS、LS两种方法进行对比分析,以说明LE方法的有效性。
本文所有数据处理均使用Python语言。
1 线性EIV模型参数的LASSO估计
线性EIV模型的矩阵形式为[7-10,13]
y-ey=(A-EA)β,
(1)
式中:y=(y1,y2,…,yn)T表示被解释变量观测值;ey=(e1,e2,…,en)T表示y的随机误差;A=(aij)n×(m+1)表示解释变量观测值矩阵;EA=(eij)n×(m+1)表示A的随机误差矩阵;β=(β0,β1,…,βm)T表示未知参数向量;eA=vec(EA)是将EA按列向量化后得到的列向量;随机误差向量
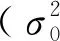
(2)
记
Q0=P-10,Q1=P-11,
(3)
式中:⊗表示矩阵的Kronecker积[14];Py为y的权阵;PA为A的权阵;P0为A的列向量权阵;P1为A的行向量权阵。关于伪逆阵的求解见文献[15]。
文献[7]给出了该模型的WTLS数值解迭代算法。本文基于结构风险最小化原则[16],借鉴LASSO回归思想[17],在所有数据加权残差平方和(反映拟合优度)的基础上加上一个1-范数惩罚项(反映复杂度),即为线性EIV模型参数的LASSO估计(LE)方法,模型如下:
(4)
式中μ≥0为惩罚参数。令
Φ(ey,eA,λ,β)=
2λT(y-ey-(A-EA)β)=
2λT(y-Aβ-ey+(βT⊗In)eA),
(5)
又令
(6)
(7)
(8)
(9)
在式(9)中
r=(r0,r1,…,rj,…,rm),
(10)
由式(6)、式(7),得
ey=Qyλ,
(11)
eA=-(Q0⊗Q1)(β⊗In)λ=
-(Q0β⊗Q1)λ。
(12)
根据恒等式[7]
vec(HFGT)=(G⊗H)vec(F),
(13)
并由式(12),得
EA=-Q1λ(Q0β)T=-Q1λβTQ0。
(14)
将式(11)、式(12)代入式(8),得
y-Aβ=ey-(βT⊗In)eA=
Qyλ+(βTQ0β⊗Q1)λ,
(15)
因此,有
λ=(Qy+(βTQ0β)Q1)-1(y-Aβ)。
(16)
将式(16)分别代入式(11)、式(14),得
ey=Qy(Qy+(βTQ0β)Q1)-1(y-Aβ),
(17)
EA=-Q1(Qy+(βTQ0β)Q1)-1(y-Aβ)βTQ0。
(18)
将式(16)、式(18)代入式(9),得
(19)
式中:
v=(y-Aβ)T(Qy+(βTQ0β)Q1)-1Q1·
(Qy+(βTQ0β)Q1)-1(y-Aβ)。
(20)
由式(19),得
β=(2AT(Qy+(βTQ0β)Q1)-1A-2vQ0)-1·
(2AT(Qy+(βTQ0β)Q1)-1y-μr),
(21)
式(21)是优化问题(4)的最优解所满足的条件方程。令
U=2AT(Qy+(βTQ0β)Q1)-1A-2vQ0,
(22)
V=ββT,
(23)
W=2VAT(Qy+(βTQ0β)Q1)-1,
(24)
则式(21)可写为
VUβ-Wy=-μVr,
(25)
考虑式(25)等号两边的第j个分量,有
(VUβ-Wy)j=-(μVr)j,j=0,1,…,m。
(26)
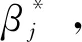
由以上分析,可以给出LE方法数值解的求解算法如下:
(1)取初始值v(0)=0,β(0)=N-1C,[N,C]=ATPy[A,y],i=0,并给定迭代误差允许范围ε。
(2)计算第i+1次迭代β(i+1):
①j=0
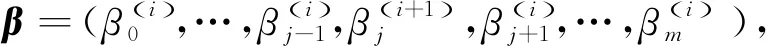
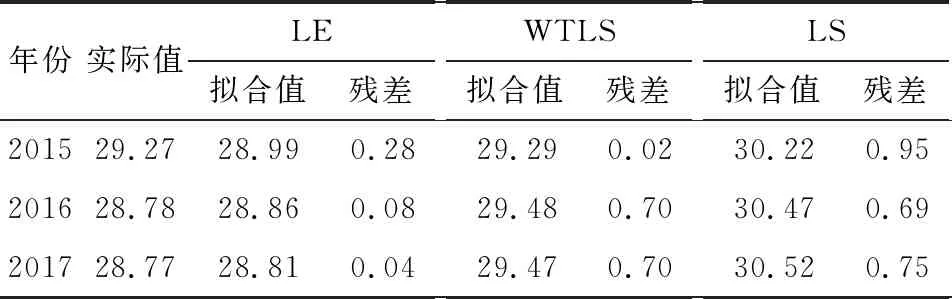
③如果intercept>yA,则rj=-1,否则如果intercept ⑤j=j+1 ⑥如果j≤m,则转② (4)i=i+1,转(2)。 (5)结束。 在实际应用时,算法中的权阵通常赋予特殊形式[7]。 本文利用LE方法对2001—2017年我国个人卫生支出占比(y)的影响因素进行分析,并与WTLS、LS两种方法进行比较,以进一步验证本方法的有效性。 我国个人卫生支出占比的影响因素很多,根据相关文献[19],本文从卫生总费用、人口、政策、经济、医疗技术水平、医疗服务供给收入6个观察点选取了12个指标作为影响我国个人卫生支出占比的因素,详见表1。 表1 个人卫生支出占比影响因素 本文所用的个人卫生支出占比及其各影响因素指标数据均来源于中国统计年鉴以及中国卫生统计年鉴。其中,2001—2014年的14组数据作为训练数据集,2015—2017年的3组数据作为测试数据集。 2.3.1 多重共线性诊断 本文对上述12个解释变量做多重共线性诊断,结果见表2。由表2可以看出:9—13维度的特征值约等于0,并且其条件索引的值远大于10,说明解释变量间存在较严重的多重共线性。 表2 多重共线性诊断 2.3.2 基于LE方法的建模 为计算方便,本文对权阵进行了一定的简化,即令 P0=diag(0,1,1,1,1,1,1,1,1,1,1,1,1), P1=I14,Py=I14。 给定ε=0.5×10-8,通过K-折交叉验证法[17](这里K=10)选取惩罚参数μ=0.002 6,参数估计结果为 0.123 0X4+0.000 2X7-0.036 2X8。 (27) 由此可知,12个指标中7个指标的系数已压缩为0,其影响被完全忽略,仅留下5个指标,还可以看出:政府卫生支出占卫生总费用比例、社会卫生支出占卫生总费用比例、城镇人口比和婴儿死亡率对个人卫生支出占比都呈现负向影响;人均GDP对个人卫生支出占比呈现正向影响。 2.3.3 对比分析 本文分别采用WTLS、LS两种方法对回归模型参数进行估计,其结果为: 1.598 1X3-0.273 4X4-0.492 4X5- 0.086 0X6-0.000 3X7-0.009 1X8- 2.327 5X9+0.504 3X10+0.000 7X11+0.000 1X12, (28) 1.548 9X3-0.261 4X4-0.466 5X5- 0.091 4X6-0.000 3X7-0.007 2X8- 2.327 5X9+0.519 2X10+0.000 7X11+0.000 1X12。 (29) 可以看出,在WTLS和LS两种方法中,政府卫生支出占卫生总费用比例、社会卫生支出占卫生总费用比例、城镇人口比、失业率、卫生总费用占GDP比例、人均GDP、婴儿死亡率和每千人口床位数对个人卫生支出占比都呈现负向影响;65岁及以上老年人口比、每千人口医生数、城镇人均纯收入和农村人均纯收入对个人卫生支出占比都呈现正向影响。 但是,WTLS和LS两种方法的估计都存在系数正负号不符合实际的状况,如人均GDP的系数为负,这与实际情况不符。因为随着人均GDP的增长,生活水平越来越好,人们更加注重身体健康,从而会促进个人卫生支出占比。该结果可能是由解释变量间多重共线性的影响造成的。 根据上述三种估计方法所求的回归方程对测试数据集进行预测,并与实际数据进行对比,结果见表3。显然,LE方法得到的预测值更准确。 表3 个人卫生支出占比预测值与实际值对比 将本文提出的LE方法与WTLS、LS两种方法进行对比分析,结论如下: 1)LE方法全部系数正负号都符合实际,但在WTLS与LS两种方法中,部分系数正负号不符合实际。 2)LE方法预测精度更高。LE、WTLS和LS相对于实际值的均方根误差分别为0.169 7、0.571 7、0.806 6,可见LE方法的精度更高。 3)LE方法的拟合优度更高。各方法的决定系数R2如下:WTLS的为0.990 4、LS的为0.960 5、LE的为0.999 1,可见LE的拟合效果更好。 本文提出了基于结构风险最小化原则的线性EIV模型参数的LE方法,并给出了其数值解的快速迭代算法。如果直接由条件方程设计求解算法,那么算法的效率不高,为此本文做了技术上的处理。另外,算法还考虑到了解的唯一性问题。为了说明该方法的有效性,本文结合实证与WTLS、LS两种方法进行了对比分析,结果表明: LE方法能够进行高维回归系数压缩,实现降维的目的,明显提高预测精度,具有更强的泛化能力,达到更高的拟合优度。这样的结果和文献[20]相比更理想。本文的研究还需要进一步完善,如可以针对参数估计的统计性质进行深入探讨等。
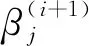
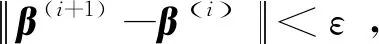
2 模型比较
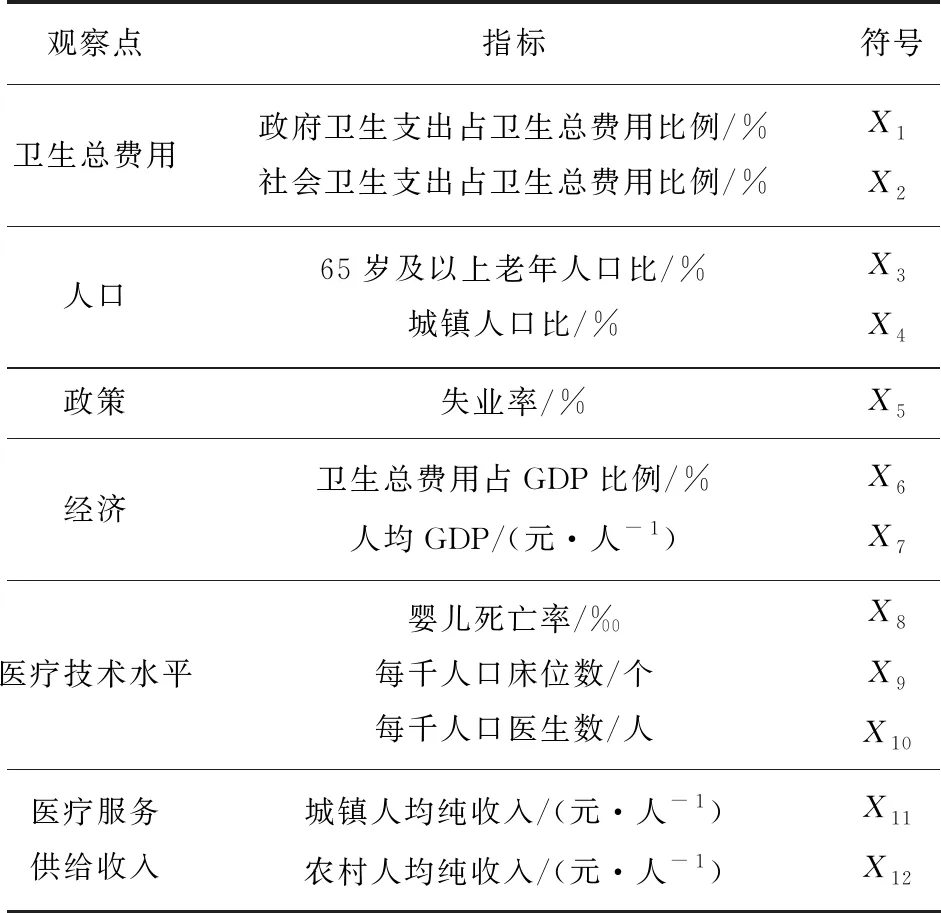
2.1 指标体系构建
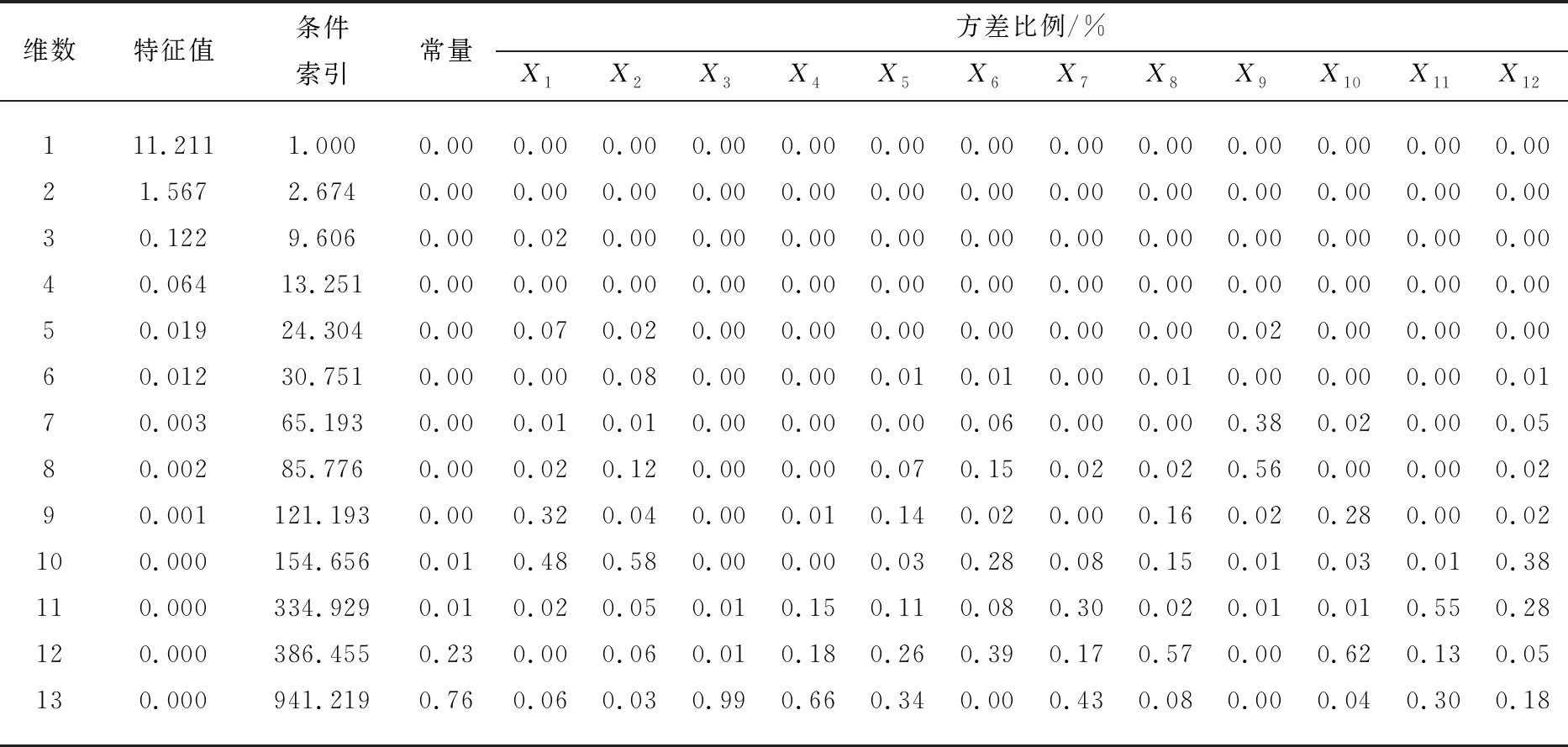
2.2 数据获取
2.3 模型建立与对比分析
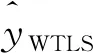
3 结束语

