基于随机森林算法的港口集装箱吞吐量预测方法

谢新连，王余宽,2，许小卫，马 昊

(1. 大连海事大学 交通运输工程学院,辽宁 大连 116026； 2. 武汉理工大学 航运学院，湖北 武汉 430063)

0 引 言

港口作为海运网络的重要节点，它的发展与所在区域向海经济发展互为支撑。港口集装箱吞吐量是港口管理部门制定港口发展规划的主要依据之一，如何更加准确地预测集装箱吞吐量一直是学术界和工程界的研究热点。

总结已有的研究文献，港口集装箱吞吐量预测方法主要包括以下几种：指数平滑法[1]、多元回归分析法[2]、灰色预测法[3]、神经网络预测法[4-7]、组合预测法[8-9]等，各个模型具有以下特点：指数平滑法是对单一变量进行建模分析，难以计算特征变量的影响，对波动幅度大的数据适应性也较差；多元回归分析考虑特征变量对集装箱吞吐量的影响，但无法避免特征变量间的共线性效应；灰色模型虽然所需的参数较少，但其快速递增和衰减的特性导致只适用于短期预测；神经网络对离散、非线性数据有较好的应用效果，但对训练样本容量需求较大，而且容易陷入局部最优；组合预测在计算权重值大小时，精度很难保证。综上分析，可见已有的方法的局限性限制了港口集装箱吞吐量预测精度，因此提出对集装箱吞吐量预测方法的研究是十分必要的。

随机森林算法(random forest algorithm，RFA)是一种基于决策树理论的机器学习算法，能够评估所有特征变量的重要性，同时避免线性分析所面临的多元共线性的问题，L. BREIMAN[10]描述了随机森林算法进行多维变量重要性排序以及决策树构建等技术。随机森林算法的优势在于集成了多棵决策树，可以处理数以千计的特征变量，实验显示该算法计算速度较快，准确率较高。目前随机森林算法在短时交通流预测[11]、热轧带钢质量预测[12]、太阳能辐照度预测[13]等方面已被应用。

笔者将RFA应用于港口集装箱吞吐量的预测，并将RFA与多元回归分析、三次指数平滑和BP神经网络的预测结果比较，结果表明：基于RFA的预测方法预测准确性更高。

1 随机森林算法

RFA通过组合个体决策树，并基于投票机制进行决策，包含分类和回归两种模型，其中分类模型基于决策树预测值的多数票进行决策，回归基于决策结果的平均值进行决策。 在训练阶段，从初始样本集合中进行bootsrap抽样(随机且有放回地抽取), 并对每个bootsrap样本建一棵决策树，每棵树即为一个弱分类器，通过建立多个弱分类器对高维数据间的内在联系进行分析，然后将多个弱分类器组合, 通过投票机制得出决策结果，进而构成一个强分类器，一个包含K棵决策树的RFA决策模型结构如图1。

RFA的特点是：每棵决策树分割节点的数量是从样本集特征数量中随机选择出来，然后通过定量分析对该节点数量所产生效果进行评估，以决定该棵决策树的分割节点数量。为所有决策树随机提供分割节点数量，这种随机性使得由众多决策树结合起来得到的集合决策树拥有更好的预测性能。

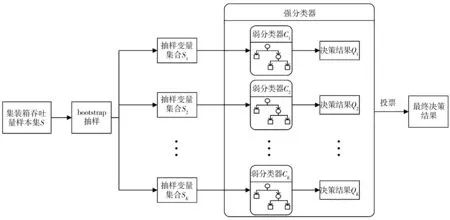
图1 RFA决策树构建示意Fig. 1 Schematic diagram of decision tree construction of random forest algorithm (RFA)

2 集装箱吞吐量预测模型

2.1 随机森林结构

RFA预测模型参数包含决策树数量和节点变量个数。决策树数量决定预测模型的泛化能力，节点变量个数为单棵决策树的分裂节点数量，影响决策精确度。一般而言，泛化误差是在使用bootstrap抽样法抽样时，样本未被抽中导致的，假设样本数量为N，则样本被抽中的概率为[1-(1-1/N)N]，当N趋向于无穷时，[1-(1-1/N)N]收敛于0.632，即在总样本集中存在36.8%的样本未被抽中，这部分样本称为袋外(out-of-bag，OOB)样本，利用OOB样本计算模型的泛化误差称为OOB估计。OOB估计步骤为：

1)将各个训练集分别作为OOB样本，计算RFA决策树各弱分类器的决策结果。

2)以投票模式选举得到各个OOB样本的最终决策结果。

3) 计算每一棵决策树的OOB估计结果，即每一棵树样本分类错误数量与样本总数的比率。模型的泛化误差计算式为：

(1)

式中：EK为包含K棵决策树的RFA模型的泛化误差；ε[yn,Ck(xn)]为对第n个训练样本的OOB估计误差进行计算；xn为第n个训练样本；yn为第n个训练样本的分类结果；Ck(xn)为K棵决策树对xn的决策结果。

对于组成RFA模型的每棵决策树，均可计算得到一个OOB估计误差，进而通过式(1)计算得到模型的泛化误差EK。计算不同决策树数量时模型的泛化误差，当泛化误差最小时即获得最优决策树数量。而节点变量个数的最优值一般为特征变量数量的1/3，实例数据中特征变量为17个，则需要分别计算并比较节点变量个数为5和6时的模型决策误差，选取决策误差较小时对应的值为RFA模型的节点变量个数。

2.2 变量重要性分析

为了提高RFA的预测精度，需要确定影响港口集装箱吞吐量相关变量，并计算其影响程度。(mean decrease in accuracy, MDA)是用来衡量变量重要性的参量，MDA基于OOB估计来计算，其值直接表示该变量对模型预测准确度的降低程度，值越大表示该变量对港口集装箱吞吐量的影响越大。用Mv表示第v个变量的MDA值，其计算公式为：

(2)

式中：t为RFA模型的决策树数量；en为第n个样本的OOB估计误差。

对所有变量进行多次重要性分析，求其分值平均值并排序，从样本集所有特征变量中排除冗余特征变量，并对分值计算结果结合实际分析，筛选出V个对集装箱吞吐量影响程度较大的特征变量，组成预测模型的变量集合。

2.3 决策模型

基于筛选出的具有重要影响的特征变量样本集，运用bootstrap方法随机抽得b个样本，然后从所有特征变量中随机选取v′个变量，即得到一个样本集。重复以上操作A次，则得到由A个独立样本集形成的总样本集。对各样本集构建决策树模型，得到包含K棵决策树的随机森林。最后通过每棵树投票形式寻找得分最高结果作为预测的结果。最终获得的RFA模型为：

(3)

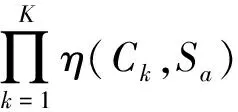
2.4 评价指标选取

为验证随机森林算法对集装箱吞吐量的预测效果，采用相对误差Er(relative error)、平均绝对百分比误差EMAP(mean absolute percentage error)、均方误差EMS(mean square error)、和均方根误差ERMS(root mean square error)4个指标来检验模型的预测精度。ER用来评价预测方法中每一个测试样本的预测效果，EMAP、EMS及ERMS作为模型整体预测效果的误差检验方法，4个指标计算如式(4)～式(7)：

(4)

(5)

(6)

(7)

式中：ER,n为第n个样本的相对误差；xn,r和xn,p分别为第n个测试样本的真实值和模型预测值；N为测试样本数量。

3 应用实例

3.1 变量获取

从中国交通运输统计网、《大连市统计年鉴》、《辽宁统计年鉴》和《中国统计年鉴》中获取所需数据，时间域为2000年—2019年，其中2000年—2014年数据作为预测模型的训练样本集，2015年—2019年的数据为验证样本。

影响集装箱吞吐量预测的环境因素较多，表1统计了港口集装箱吞吐量数据和可能对集装箱吞吐量产生影响的17个特征变量，包括区域生产总值、周边港口集装箱吞吐量、东三省对外贸易量等，实验选取18个变量的所有数据构成预测模型的总样本集。

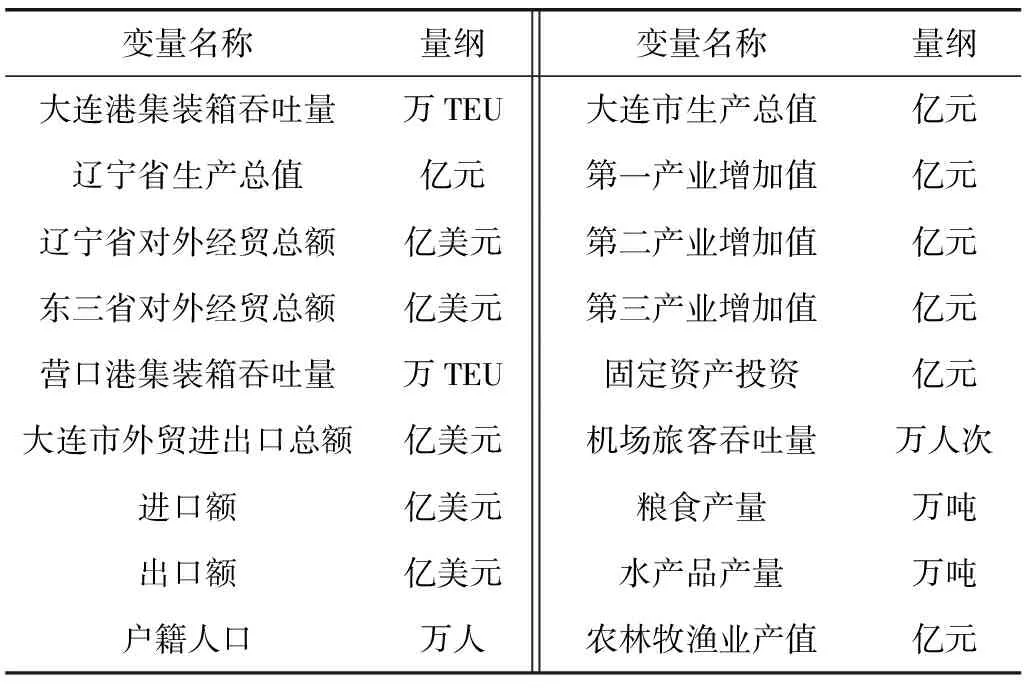
表1 模型变量Table 1 The model variables

3.2 模型参数优选

一般而言，节点变量个数为特征变量个数的1/3，本例中通过实验得到节点变量个数为6时，RFA预测误差最小。图2给出了不同的决策树数量所导致的模型误差，当决策树数量为500时模型误差达到最低点，因此，选择决策树数量为500。

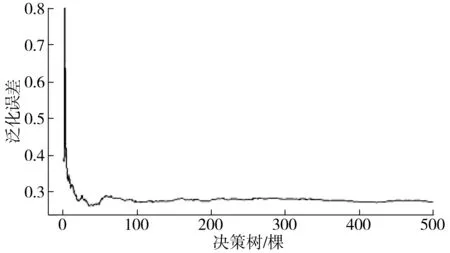
图2 模型决策树误差Fig. 2 Model decision tree error

3.3 变量重要性分析及特征优选

根据MDA分析原理得变量重要性分值，如表2，第三产业增加值、营口港集装箱吞吐量、大连市生产总值的重要性较大，分值在7以上；辽宁省生产总值、辽宁省对外经贸总额等6个变量重要性分值在5～7之间；而机场旅客吞吐量的重要性分值则不足3，说明该变量对模型的增益效果很低。

根据变量重要性排序，依次叠加选取重要性最高得变量，将所选变量组成特征集合进行集装箱吞吐量预测。随着特征变量个数得增加，模型预测准确度变化趋势如图3。变量数目小于5时，预测准确度随变量数目增加而显著提升；在变量数量为9时，预测准确度为95.66%，达到峰值；在变量数目为16时，即把机场旅客吞吐量加入特征变量集合时，预测准确度出现较大波动。由此看出，预测准确度并非严格随变量数目的增加而升高，这说明部分变量对港口集装箱吞吐量预测有干扰，此类冗余特征的删除有助于提升预测准确度。因此，研究提取重要性排序前九的变量数据进行预测建模，筛选出的变量既可用于随机森林模型预测，亦可在其他预测方法中应用。

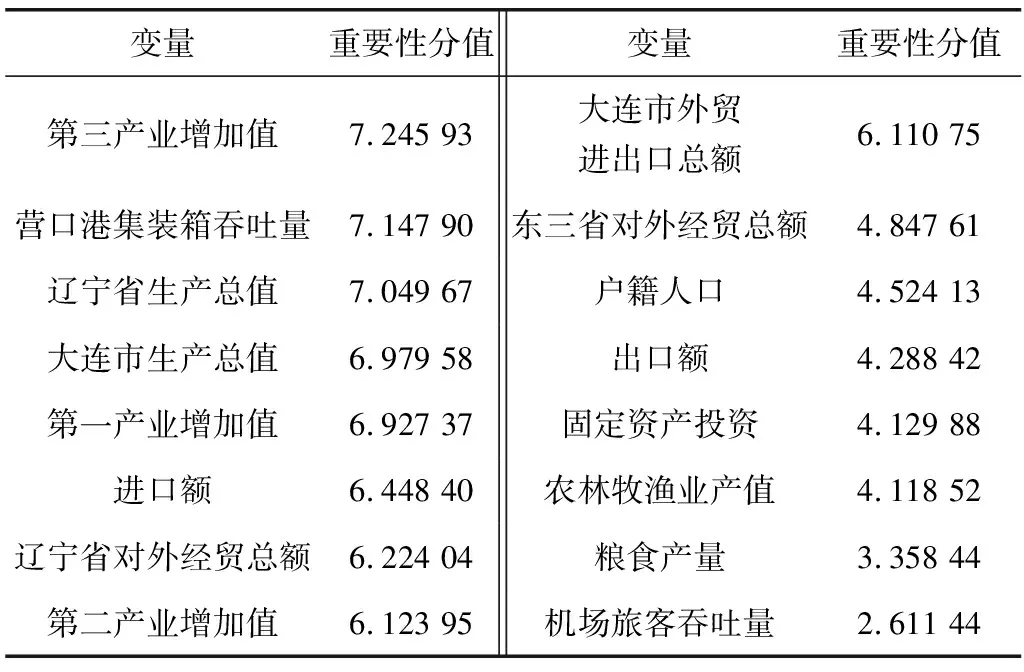
表2 变量重要性得分Table 2 Importance score of variables

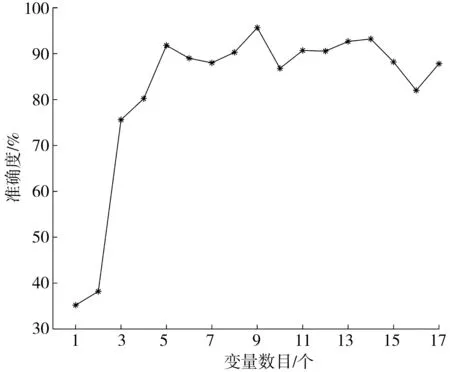
图3 预测准确度与优选变量数目关系Fig. 3 Relationship between prediction accuracy and the number of preferred variables

3.4 预测结果分析

将RFA预测结果与多元回归分析法、三次指数平滑法以及BP神经网络预测法的预测结果对比分析。4种方法对2015年—2019年大连港集装箱吞吐量的预测值及误差如图4，显而易见：相比于其它3种方法，RFA预测结果更接近实际值，并且在不同年份的预测波动较小。

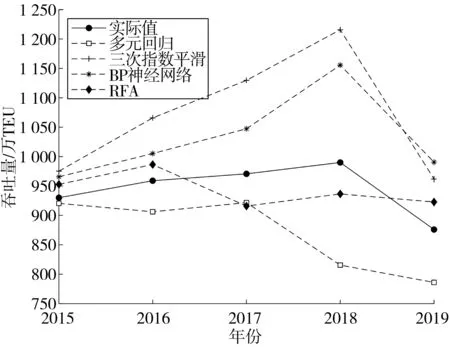
图4 4种模型预测值Fig. 4 Forecasting results of four kinds of models

如表3为4种模型的预测值及误差，其中平均误差值为各年预测误差绝对值的平均值。RFA预测值平均误差率为4.34%，各年绝对误差最大值为5.65%，而多元回归和BP神经网络的平均误差率均接近10%，三次指数平滑平均误差率大于10%，绝对误差率高达22.8%，可见RFA预测最接近实际值。

图5展示了4种模型预测结果总体相对误差分布，可以看出，多元回归相对误差为负值，三次指数平滑和BP神经网络均为正值，说明此3个模型预测结果均出现偏离实际值现象，而随机森林相对误差在0附近说明其预测结果贴合实际值。据图4和图5可知，随机森林模型在各个年份可提供较为准确的单点预测效果。

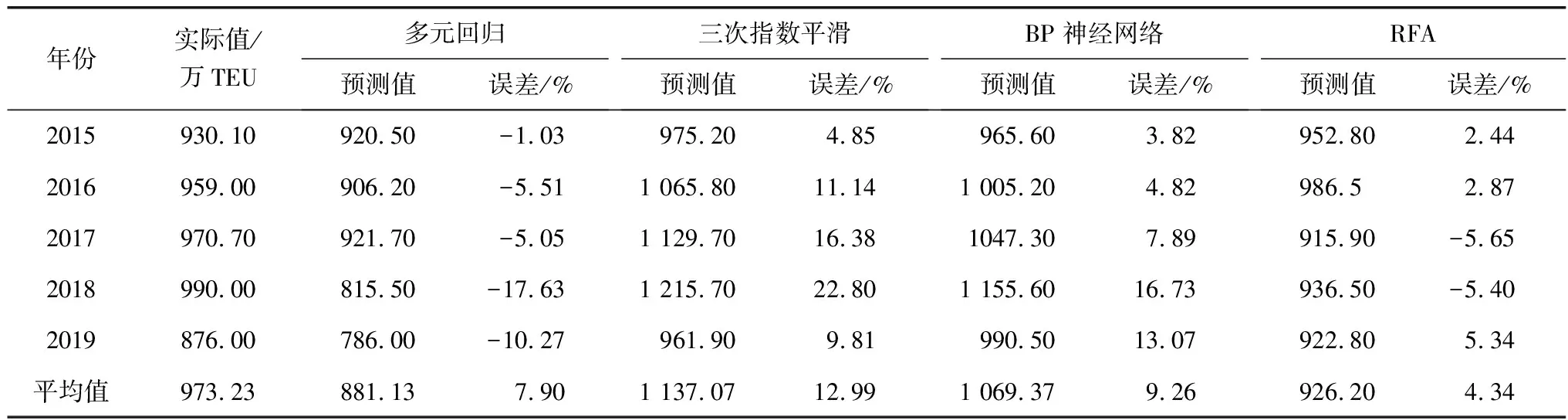
表3 模型预测值及误差Table 3 Model prediction values and errors

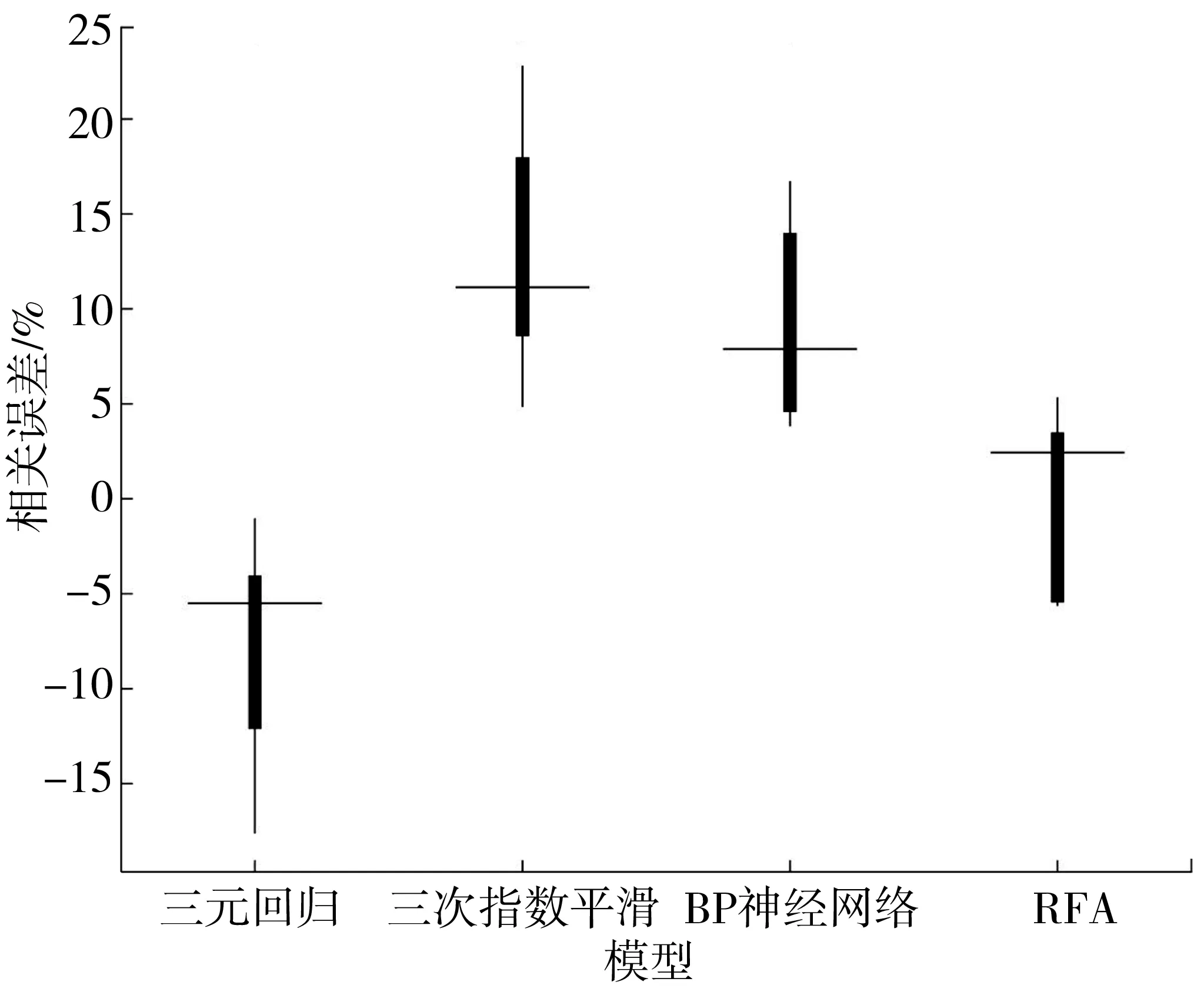
图5 4种模型预测箱线图Fig. 5 Boxplot diagram of four kinds of models

为了进一步验证RFA的预测性能，对4种模型的EMAP、EMS和ERMS指标进行分析，如表4。可见，RFA的EMAP低于5%，其EMS仅为其它模型的20%左右，ERMS值也在各个模型中最低。在各个指标表现上，多元回归和BP神经网络表现较为相似，而三次指数平滑EMAP达到12.99%，在各个指标中表现均为最差。可知，随机森林预测各项误差评价指标上均优于其他3个预测方法，预测性能优势显著。

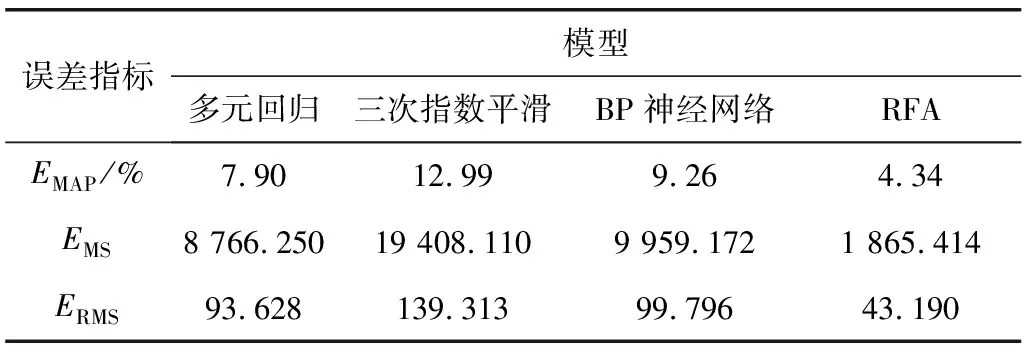
表4 模型评价指标Table 4 Model evaluation index

通过实验分析，RFA在进行具有时间特性的港口货物吞吐量预测中，预测结果更接近实际值，预测误差也明显低于BP神经网络模型、多元回归分析法和三次指数平滑法。同时，RFA在保证准确预测吞吐量整体变化趋势的基础上，在较长时间内对各个年份的单点预测结果也较为接近实际，提高了吞吐量预测的准确性。

4 结 语

港口集装箱吞吐量的预测与复杂的环境影响变量相关，随机森林算法消除了特征变量的共线性影响，并基于MDA分析各变量的影响程度，筛选出有重要影响的特征变量，其中第三产业增加值重要性分值最高，营口港集装箱吞吐量重要性排名第二。第三产业的发展是经济发展的关键体现，而营口港作为大连港的近邻港口，则会因同质竞争而出现吞吐量间的重要关联性，可以预见，重要变量分析结果将有助于分析港口发展与经济发展的关联性，辅助港口管理人员对港口间协同发展进行合理规划。

根据变量优选结果对2015年—2019年大连港集装箱吞吐量进行预测，与三次指数平滑法、多元回归分析和BP神经网络的预测结果相比误差更小，预测性能更优。一定程度上预测结果将有助于港口管理人员更好地规划港口货源供应、货场分布、泊位布局以及水陆交通枢纽建设等。根据大连自贸港建设规划研究，目前辽宁省内港口间存在货源分布差异大的现象，这导致部分港口出现货源过量而无处安放问题，通过吞吐量预测可分析得到港口货物需求量，进而根据需求提供货物量，这将有助于港口规划货源供应以及货场分配等，更好地节约和利用社会资源。

随着海洋强国战略的部署和实施，航运业向着智慧航运的方向发展。应用随机森林算法预测港口集装箱吞吐量，更加准确、高效、合理地助力港口建设，助力政府推进智慧航运发展。