基于教与学优化的可变卷积自编码器的医学图像分类方法
李 薇,樊瑶驰,江巧永,王 磊,徐庆征
(1.西安理工大学计算机科学与工程学院,西安 710048;2.陕西省网络计算与安全技术重点实验室(西安理工大学),西安 710048;3.国防科技大学信息通信学院,西安 710106)
0 引言
自编码器(AutoEncoder,AE)[1]是一种以复现输入为输出的神经网络,它将输入数据以向量形式编码,然后重构原始图像以学习其数据特征。AE 由输入层、隐含层和输出层组成。从输入层到隐含层的转换称为编码器,从隐含层到输出层的转换称为解码器。编码器将输入压缩成一个潜在空间,解码器是编码器重构后的输出。堆叠自动编码器(Stacked AE,SAE)[2-3]是一种简单自动堆叠编码器模型。该模型通过获得更深层的网络模型,以提高算法的准确性。目前,SAE 在图像分类领域具有显著的性能。
大量文献表明,相邻信息是解决图像相关问题的关键因素[4-6]。采用SAE 必须预先转换成矢量形式,其次,不断地堆叠不仅会加深其原有结构,也会逐渐降低性能,增加复现难度,从而难以有效地解决高维问题。为了解决这个问题,Masci 等[7]提出了卷积自编码器(Convolutional AE,CAE),它可以很好地扩展到高维输入,并直接应用于二维图像结构。卷积神经网络(Convolutional Neural Network,CNN)[8-9]是一种典型的深度学习模型,具有权值共享、局部感受野、池化等特点,在解决许多实际问题时表现出比较好的性能。
在CAE 中,编码器由一个卷积层和一个池化层组成,解码器只包括一个反卷积层。CAE 在处理数据方面具有一定优势,然而在解决数据量大且复杂问题时性能会下降,因此很多学者提出了CAE 的改进算法。Kavukcuoglu 等[10]提出堆叠卷积稀疏编码,其特点是在解决实时问题时推理速度更快;Du 等[3]提出一种基于分层训练优化的层叠卷积去噪自编码器(Stacked Convolutional Denoising AE,SCDAE),以解决传统的监督模型需要大量标记数据的问题;Li 等[11]提出一种完全卷积的自编码器体系结构,该结构采用端到端的方式,将特征学习和聚类组合在一起进行训练,以获得更好的性能;Lin 等[12]提出一种深度重构模型——用重建的自编码器堆叠出卷积神经网络(CNN for Reconstruction,CNNR),以解决空间信息的丢失问题;Yu 等[13]提出流形正则化堆叠去噪自编码器(Manifold Regularized Stacked Denoising AutoEncoder,MRSDAE)以优化深度神经网络(Deep Neural Network,DNN)参数和结构。
演化算法(Evolutionary Algorithm,EA)是近年来流行的模拟自然选择和适者生存机制的随机搜索算法,在数学优化领域受到广泛关注,因此许多学者用演化算法优化CNN 的参数和结构。Sun 等[14]提出了一种灵活的CAE(Flexible CAE,FCAE),该算法利用粒子群优化(Particle Swarm Optimization,PSO)算法自动搜索CAE 的最优结构,并将最优结构堆叠为CNN,解决图像分类问题;Gao 等[15]提出基于梯度优先粒子群优化(Gradient-priority PSO,GPSO)的CNN 识别算法以解决情绪任务。
由于深度神经网络在图像分析中具有显著的效果,因此被应用于医学图像分析,以帮助医护人员分析影像[16-17]。Moon 等[18]设计用于乳腺肿瘤诊断的计算机辅助诊断(Computer-Aided Diagnosis,CAD)系统,其特点是使用一种结合不同图像内容表示的图像融合方法。
医学图像是分析患者病情的一个重要依据,而医学图像分类是以医学影像为基准识别图像类别,以帮助医生及时判断患者病情,制定治疗方案。然而现有医学图像数据集大多数没有统一的分辨率,且不符合病情诊断的标准图像,导致对病情无法做出及时准确的判断,延缓了治疗进度,因此通常采用人工对医学图像进行分类,而人工分类技术良莠不齐,影响分类精度。虽然深度神经网络能够用于医学图像分类,但分类精度不高,且需要大量时间进行手动调整深度学习模型参数,因此,自动优化神经网络模型参数以提高医学图像分类精度是目前迫切需要解决的重要问题。
综上所述,将演化算法用于神经网络可以构建比较好的网络结构,提高算法性能。然而经典的优化算法,如粒子群优化算法,其本身具有权重、学习因子等参数,而这些参数的选择是否合适,将影响算法的性能。有鉴于此,本文采用参数较少的教与学优化(Teaching-Learning-Based Optimization,TLBO)算法[19],并对经典的TLBO 进行改进,设计基于TLBO的结构优化(TLBO Architecture Optimization,TLBOAO)算法,用TLBOAO 优化卷积自编码器的结构。在卷积自编码器的基础上,设计基于TLBO 的可变卷积自编码器(TLBO Variable CAE,TVCAE),然后堆叠为卷积神经网络,并将其用于求解医学图像分类问题,以提高分类精度。
本文的主要工作如下:
1)提出TLBOAO 算法,通过设计新的编码策略,将可变卷积自编码器的隐藏结构编码到每个个体中,从而优化CAE结构。
2)提出TVCAE 算法,充分利用最优个体信息,使算法朝着更有希望的区域搜索,在有限计算资源下快速找到最优结构。
3)将TVCAE 算法用于求解医学图像分类问题。
1 相关工作
1.1 卷积自编码器
CAE 包含三层:
1)卷积(conv):卷积的目的是提取输入图片的不同特征。卷积层的输出是对其输入和权值的卷积运算(*),也称为核或滤波器。
2)池化(pool):池化用于降维,一个池化层可以是最大池化或平均池化,在其输入的r×c窗口内进行采样操作(r和c分别表示窗口的长与宽),减少输出参数的数量。
3)反卷积(d_conv):反卷积是对需要重建的图像进行反卷积运算。
CAE 的数学形式为:

其中:conv(·)是卷积操作;pool(·)是池化操作;d_conv(·)是反卷积操作;σ是激活函数;b和c是偏置项;H和y分别是卷积学习特性和池化学习特征;是x的重建结果。
以图像分类为例,用图像的宽度、高度和通道数量表示一张图片,为了便于分析,图1 表示一个通道数为1 的二值图像(Binary Image)的CAE 的结构。
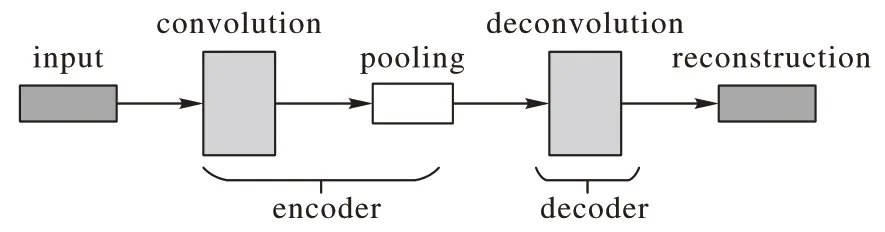
图1 CAE的结构Fig.1 Structure of CAE
1.2 教与学算法
TLBO 算法[19]是近些年比较流行的EA 之一。TLBO 算法模拟课堂教学和学习过程,分为教师教学和学生学习两个阶段。
教师教学阶段是指教师通过教学提高学生的知识水平。教学过程如式(4)所示:

其中:Xi是第i个学生;ri由[0,1]内的随机数组成;T是班级教师;TF是教师因子;Mean是当前班级平均成绩。TF的更新如式(5)所示:

学生学习阶段是指学生相互交流、学习知识,丰富知识。学习阶段如式(6)所示:

其中:Xi和Xj分别表示第i个和第j个学生且i≠j;f(·)是要优化(最小化)的目标函数。
2 基于TLBO可变长度的CAE
传统的深度学习网络结构在优化不同数据集时需要对模型参数进行调优,而传统手工调优的方式十分耗时,为了实现自动优化深度学习网络结构和参数,文献[20-22]利用粒子群优化算法和差分进化(Differential Evolution,DE)算法优化深度学习网络参数,以提高算法性能。然而粒子群优化算法和差分进化算法自身有很多参数,且算法的性能在很大程度上依赖于参数,因此在进行优化时需要调整参数。同时,由于原始的CAE 长度是固定的,所以难以堆叠出复杂的新型卷积神经网络结构,如Alexnet[23]和VGGnet[24]。有鉴于此,本文利用TLBO 算法参数少的特点,提出了TLBOAO 算法,并设计了TVCAE。
2.1 TVCAE算法
在基本的CAE 上引入TLBOAO 算法,从而形成TVCAE,其可变结构如图2 所示。通过堆叠TVCAE,构造深层次的复杂网络,减少训练深层网络结构的资源消耗。

图2 TVCAE的结构Fig.2 Structure of TVCAE
2.2 TLBOAO算法
2.2.1 编码策略
在初始化种群时,改进基本的TLBO 算法,设计一种新型编码策略,即将一个TVCAE 的隐藏结构编码到每个可变长度的个体中。表1 是TVCAE 中卷积层和池化层编码信息。图3 是3 个TLBOAO 中编码个体示例,其中以卷积核大小作为卷积层参数,以步长作为池化层参数。图4 是隐藏结构编码,其中以卷积核大小和特征映射数量作为卷积层参数,以步长作为池化层参数,TLBOAO 算法总框架如算法1 所示。T表示教师,即最优个体。算法中池化层和卷积层的计算规则一致。


表1 在TVCAE的卷积层和池化层中编码信息Tab.1 Encoded information in convolutional layer and pooling layer of TVCAE

图3 三个来自TLBOAO的不同编码信息的个体Fig.3 Three individuals with different encoded information from TLBOAO

图4 TLBOAO的隐藏结构编码Fig.4 Hidden structure coding for TLBOAO
2.2.2 初始化种群
个体的一个维度表示一层卷积层或者池化层,用TLBOAO 优化参数时,对每一维(每一层)的参数进行优化,并构造相应的层。初始化种群如算法2 所示。


2.2.3 教师教学阶段
在教学阶段,首先随机选择一个个体Xj,比较Xj、T(教师)和当前个体Xi的长度,如果三个个体的长度相等,则教学操作如下:

如果三个个体的长度不相等,令Min为三个个体的最小长度,教学操作如下所示:

其中:Xi和Xj分别表示第i个和第j个个体,且i≠j;M是当前班级平均成绩,即所有个体每一维的平均值,如果某一维平均值为空,则分配一个随机初值;D是Xi个体搜索空间的维数。图5 是3 个来自TLBOAO 的不同编码信息的个体(图3)的平均成绩的计算示例。以卷积层的计算为例,图3 中3 个个体的三层卷积核平均值分别为,则图5 对应的三层的卷积核平均值为4、3 和4。池化层和卷积层的计算规则一致。

图5 图3中3个个体的平均值Fig.5 Average values of three individuals in Figure 3
为了避免新产生的个体newXi的位置超出搜索空间,newXi更新如下:

其中:Xmax和Xmin分别表示搜索空间的上界和下界。
教学阶段的伪代码如算法3 所示。


2.2.4 学习阶段
在学习阶段,充分利用性能比较好的个体信息,以加快算法收敛。对于每一个个体Xi,其学习过程步骤是:首先,在当前种群中随机选择两个个体Xj,Xq,且i≠j≠q,比较Xj和Xq,性能最差的个体定义为Xworst;再比较Xi,Xj和Xq,性能最好的个体定义为Xbest。如果Xbest、Xi和Xworst长度相等,则学习规则如下所示:

如果Xbest、Xi和Xworst长度不相等,令Min是Xbest、Xi和Xworst中的最小长度,则学习规则如下所示:

其中:Xmax和Xmin分别是搜索空间的上界和下界。学习阶段的伪代码如算法4 所示。


2.2.5 算法评价
将优化得到的个体构建成CAE 结构,其中,目标函数为重建误差函数,误差损失值为适应度值,依据FCAE[14]设置,本文算法的训练次数设置为5,伪代码如算法5 所示。

2.2.6 教师的深度训练
在算法得到的最优个体即教师的基础上,提取卷积层和池化层,再加上全连接层,构建一个CNN 结构,并使用该结构解决医学图像分类问题。通过深度训练网络模型对医学图像进行分类,深度训练过程与算法TLBOAO 评价过程相同,只是使用更大的训练次数,例如100 或200。伪代码如算法6 所示。

3 实验与结果分析
3.1 实验数据集
由于实验设备的限制,本文仅采用上海交通大学发布的医学影像领域图像数据集[25]中的乳腺超声数据集(Breast ultrasound images,BreastMNIST)[26],如图6 所示,将1×500×500 的图像重新调整为1×28×28。医学影像领域图像数据集是具有知识共享(Creative Commons,CC)许可的多个开放式医学图像数据集。通过对乳腺癌超声扫描图像进行分类,可以在早期发现乳腺癌,并让患者得到及时的治疗,减少早期死亡人数。实验使用二元分类,即正常和良性属于正常,恶性属于不正常,进行分类识别。

图6 来自BreastMNIST数据集的示例Fig.6 Examples from BreastMNIST dataset
本文将数据集按照7∶1∶2 的比率划分为训练、验证和测试集。
3.2 实验参数设置
实验主要对比同类型的卷积自编码器模型,包括卷积自编码器(CAE)[7]、灵活的卷积自编码器(FCAE)[14],以及需要手动调整参数的Alexnet[23]和VGGnet-11[24]。其中:CAE 是最早的卷积自编码器,通过堆叠为更深层次的卷积神经网络,进行图像分类任务;FCAE 是将粒子群优化算法与CAE 结合优化CAE 网络,进行图像分类任务;Alexnet 和VGGnet-11 是经典的卷积神经网络,具有较好的图像分类效果。
实验参数设置如下:
1)FCAE 中权重w的值为0.729 84,c1 和c2 的值均为1.193。
2)由于本文算法要与同类型的需要手动调整参数的卷积神经网络(CNN)结构进行对比,因此在优化每一个个体时,卷积层的最大层数设置为5,池化层的最大层数设置为1。同时,由于计算设备的限制,TVCAE 实验的批处理大小(mini-batch size)设置为32,迭代次数(epochs)设置为5,依据最先进的CNN[14,27]的约定,实验只对卷积层的参数进行研究,池化层的内核大小以及步长设置为2。
3)卷积层的特征映射数量设置为[20,100],具有宽度和高度相同大小的卷积核设置为[2,5],L2 项的系数设置为[0.000 1,0.01],L2 表示防止过拟合问题的权重衰减正则化项。在进行CNN 模型训练时,批处理大小(mini-batch size)设置为32,迭代次数(epochs)设置为100。
3.3 实验结果
表2 是本文算法TVCAE 与CAE、FCAE 在对乳腺癌超声扫描图像分类精度对比结果。TVCAE 将卷积层、池化层和一层全连接层进行组合,形成一个新的CNN 框架进行图像分类。实验结果表明,与CAE 和FCAE 相比,TVCAE 分类精度提升了0.78 个百分点。图7 是TVCAE、FCAE 和CAE 分类精度趋势图,图7 显示TVCAE 算法在40 次迭代时就趋于稳定,并且分类精度高于FCAE 和CAE。

图7 单层网络的分类精度准确率趋势Fig.7 Classification accuracy trend of one-layer networks
本文在使用CAE、FCAE 和TVCAE 对应的堆叠层进行分类精度对比时,是将每个算法的卷积层、池化层和两层全连接层进行组合,形成一个新的CNN 框架进行图像分类。表3是堆叠的TVCAE 与经典算法Alexnet、VGGnet-11,及同类型CAE 算法、FCAE 算法的实验对比结果。其中:CAE-2、FCAE-2 和TVCAE-2 分别代表2 层的堆叠网络。FCAE-3 和TVCAE-3 代表3 层堆叠网络,与Alexnet 和CAE-2 相比,TVCAE 分类精度提升了3.12 个百分点;与FCAE-3 相比,TVCAE 分类精度提升了1.56 个百分点;与VGGnet-11 相比,TVCAE 分类精度提升了0.78 个百分点。实验结果表明,使用优化的TVCAE 三层堆叠网络,不仅可以快速构建出较深的网络结构,并且分类精度可以达到不错的效果。

表2 TVCAE与CAE和FCAE的BreastMNIST分类精度对比Tab.2 Comparison of classification accuracy of TVCAE,CAE and FCAE for BreastMNIST

表3 堆叠TVCAE与Alexnet、VGGnet-11、CAE、FCAE的BreastMNIST分类精度对比Tab.3 Comparison of classification accuracy of TVCAE with Alexnet,VGGnet-11,CAE and FCAE for BreastMNIST
图8 是TVCAE-3、FCAE-3、Alexnet、VGGnet-11 和CAE-2分类精度趋势图,图8 显示TVCAE-3 算法虽然出现波动,但算法可以快速达到比较高的准确率。在大多数情况下TVCAE-3 优于FCAE-3、Alexnet、VGGnet-11 和CAE-2,且TVCAE-3 的分类精度多次达到0.9 以上。综上所述,相较于其他算法,TVCAE 算法采用可变长的编码方案,在演化的不同阶段,选择不同的演化策略,并充分利用优秀个体信息,因此性能比较好。

图8 复杂网络的分类精度准确率趋势Fig.8 Classification accuracy and accuracy trend of complex networks
本文利用教与学优化算法无参数、优化性能高的特点,优化卷积自编码器的模型参数:一方面,减少模型参数设置所需人力和时间,降低系统开销;另一方面,改变原有卷积自编码器模型的固定结构,通过优化模型参数和结构以构建更加有效的可变长度卷积自编码器。在此基础上,堆叠深度卷积神经网络进行图像分类。实验结果表明,所采用的优化算法相较于同类型算法,能够得到更有效的效果;所构建的卷积神经网络相较于其他经典方法,能够快速得到更为准确的分类结果。
4 结语
深度学习和计算机视觉技术的快速发展,为医学研究提供了新的研究方向,自动精准识别医学图像已成为医学诊断的重要技术手段之一。为了进一步提高医学图像分类方法性能,本文提出了一种基于教与学优化的可变长度的卷积自编码器算法。首先,改进基本的卷积自编码器和教与学优化算法,用教与学优化算法优化卷积自编码器网络参数和结构;其次,将卷积自编码器进行堆叠,构造新的卷积神经网络;最后,将本文算法应用于医学图像分类。实验结果表明,本文提出的算法在图像分类精度方面优于多种经典方法,是可行且有效的。

