求解工程约束问题的新型智能优化算法及展望

张孟健，王德光，2，汪 敏，杨 靖，2*

（1.贵州大学电气工程学院，贵阳 550025；2.贵州省互联网+协同智能制造重点实验室（贵州大学），贵阳 550025）

0 引言

典型的工程设计问题，如管柱设计、拉力/压缩弹簧和压力容器设计［1-2］可以用非线性规划（NonLinear Programming，NLP）［3］来表述，其数学模型可表述如下：

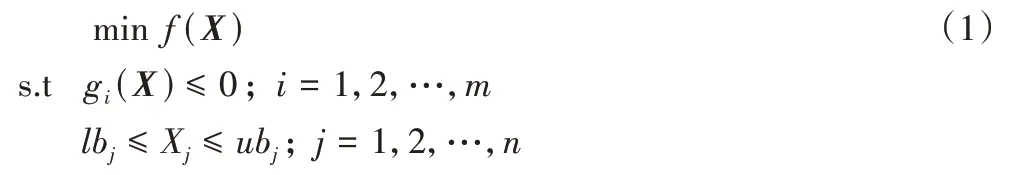
其中：X表示决策变量且X=(X1，X2，…，Xn)T；f（X）表示目标函数；gi(X)表示不等式约束；lbj、ubj分别表示决策变量Xj取值的上边界和下边界。

对于非线性规划问题中，包含了不等式约束问题、等式约束问题，以及混合式问题。针对解决不等式约束的工程优化问题，粒子群优化（Particle Swarm Optimization，PSO）算法［4］、布谷鸟算法、灰狼优化算法等仿生智能优化算法取得显著的成效。

自PSO 算法、遗传算法（Generic Algorithm，GA）［5］、蚁群优化（Ant Colony Optimization，ACO）算法［6］等智能优化算法提出以来，智能优化算法在较多的领域得到了广泛的应用，如：工程优化、粒子滤波、多目标优化等。在2010—2020 年近10 年期间，许多新的仿生智能优化算法被提出，如：蝙蝠算法（Bat Algorithm，BA）［7］、布谷鸟搜索（Cuckoo Search，CS）算法［8］、灰狼优化（Grey Wolf Optimizer，GWO）算法［9］等。在近2018—2020 年期间，群体智能优化算法作为人工智能领域的一个小的分支，得到了较大的发展。

本文选择了发表于2019—2020 年间的6 种新型仿生智能优化算法进行分析研究，即哈里斯鹰优化（Harris Hawks Optimization，HHO）算法［10］、平衡优化（Equilibrium Optimizer，EO）算法［11］、海洋捕食者算法（Marine Predators Algorithm，MPA）［12］、政治优化（Political Optimizer，PO）算法［13］、黏液霉菌算法（Slime Mould Algorithm，SMA）［14］、堆阵优化（Heap-Based Optimizer，HBO）算法［15］。首先对多个基准函数进行测试，分析它们的寻优性能；然后将6 种优化算法应用于3 种工程优化问题；最后对这6 种算法未来的研究方向进行展望。

1 相关的优化算法描述

1.1 HHO算法

HHO 算法的灵感来自哈里斯鹰探索猎物、突袭的不同攻击策略［10］。该算法是基于种群的无梯度优化技术，由于捕猎场景的动态性质和猎物的逃跑模式的多样性，哈里斯鹰可以根据实际情况选择追捕方式，即建立合理的模型，HHO算法可应用于任何最优化问题。

在寻优的过程中，HHO 算法主要有以下阶段：探索阶段（Exploration phase）、从勘探到开发的过渡阶段（Transition from exploration to exploitation）、突袭阶段（Exploitation phase）；猎物逃逸的能量参数E采用线性控制策略，且能量参数初始值E0的取值范围为［-1，1］，在突袭阶段，根据参数E的取值可分为：软围困和硬围困两种。即当|E|≥0.5 时，进行软围困；当|E|<0.5 时，进行硬围困。

文献［16］提出了一种改进的哈里斯鹰优化算法，用于优化室内到达时差（Time Difference of Arrival，TDOA）定位问题；文献［17］针对参数E提出了多种不同的改进策略，提高HHO 算法求解优化问题的寻优能力和精度。

1.2 EO算法

EO 算法是一种基于控制容积强混合型动态质量平衡，从而估计平衡状态的物理启发式算法［11］。EO 算法的原理可简述为：首先，由四个最佳粒子的浓度算数平均值组成平衡池；其次，通过质量平衡方程不断更新粒子浓度来达到寻优的效果。在EO 算法的寻优过程中，生成概率（Generation Probability，GP）作为调节参数来控制参与概率浓度更新的发生率。

文献［18］将EO 算法应用于含高比例风光新能源电网无功优化问题，并取得了较好的效果；针对多级阈值处理精度差、速度慢等问题，文献［19］提出一种自适应均衡优化算法用于优化多级阈值优化。

1.3 MPA

MPA 是基于捕食Lévy 游走策略和海洋捕食者的布朗运动以及捕食者对猎物生物觅食行为的仿生智能优化算法［12］。根据捕食者的觅食行为，MPA 的寻优过程主要有5 个方面：1）海洋捕食者对猎物、捕食者丰富区域分别采用Lévy游走策略和布朗游走，即算法采用Lévy 策略进行初始化；2）觅食时捕食者的Lévy 和布朗游走策略的比例相同，即算法的寻优过程；3）水域涡流或鱼类聚集装置（Fish Aggregating Devices，FADs）效应会对捕食者的觅食行为产生影响，即算法寻优过程的调节机制；4）捕食者与猎物运动速度不同时，捕食者会采用不同的觅食策略，即选择不同的寻优策略（局部搜索或全局搜索）；5）捕食者有着良好的记忆，且会提醒同类成功觅食的区域，即算法根据适应度值更新位置。文献［20］针对水文预测预报问题中的径流预测，提出了一种混合MPA 的自适应神经模糊推理系统的预测方法；文献［21］提出一种自适应变异策略的MPA，用于光伏参数的识别，进而提高识别精度。

1.4 PO算法

PO 算法是一种基于政治激励的新型优化算法［13］。PO算法的结构主要有五个阶段，包括：政党组建和选区分配（Party formation and constituency allocation）、选举活动（Election campaign）、政党转换（Party switching）、政党间选举（Inter-party election）和议会事务（Parliamentary affairs）。在PO 算法的寻优过程中，政党组建和选区分配阶段作为初始化，其余四个阶段循环执行至最大迭代次数或寻优精度。

文献［22］提出了一种基于基因表达数据的二元政治优化器来解决特征选择问题，并对多组生物数据进行分类。

1.5 SMA

SMA 主要是一种模拟黏菌在觅食过程中的行为和形态变化的仿生智能优化算法［14］。在SMA 中，使用权重来模拟黏菌在觅食过程中产生的正负反馈，从而形成三种不同的形态，即接近食物（Approach food）、包围食物（Wrap food）、摆动（Oscillation）。文献［23］针对光伏电池的单二极管模型和双二极管模型，提出了一种基于自适应策略的SMA 的参数估计方法。

1.6 HBO算法

HBO 算法是受企业中的等级结构（Corporate Rank Hierarchy，CRH）启发而提出的一种新型优化算法［15］。该算法的过程可分为四个步骤：1）对企业等级结构（CRH）建模；2）对下属与直接上司之间的互动进行数学建模；3）建立同事间互动的数学模型；4）员工为完成一项任务而作出的自我贡献。

1.7 分析小结

上述的6 种优化算法，按其性质可以分为三类：1）基于动物、生物等觅食行为的群智能优化算法（即HHO 算法、MPA、SMA）；2）基于社会行为的仿生智能优化算法（即PO 算法、HBO 算法）；3）基于物理性质的仿生智能优化算法（即EO算法）。

从6 种算法的结构上可知，HHO 算法、EO 算法和MPA 在寻优的机制上相近，均具有记忆性能；PO 算法是根据政治选举的特征，建立合理的模型即能达到寻优的效果；SMA 是一种基于生物觅食行为的优化算法，由于在寻优时会在多个机制间转换，增加寻优的时间；而HBO 算法在结构上是基于企业等级结构（CRH）的建模，并不能从理论上保证该结构的优越性。

2 实验与结果分析

为了分析6 种算法的寻优能力，选择了如表1 所示的10种基准测试函数。各算法的参数设置如表2 所示，迭代次数为1 000，维度为50，种群规模设为25，每个测试函数独立寻优30 次。此外，寻优仿真测试的实验环境：Windows 7 操作系统，Intel Core i5-4210U CPU @2.4 GHz，4 GB 内存，Matlab 2018a。

表1 基准测试函数Tab.1 Benchmark functions

表2 参数设置Tab.2 Parameter setting

对6 种算法的寻优性能及其有效性，本文设计了2 组对比实验：1）6 种优化算法对10 种基准测试函数（5 个单峰函数、5 个多峰函数）进行寻优仿真；2）对3 种不等式约束的工程优化问题进行应用比较。

2.1 算法复杂度

由于测试平台的不同，同一优化算法的寻优消耗时间也会不同。因此，须对算法的结构进行分析，6 种优化算法的计算复杂度详见表3。表3 中：N表示算法的种群数量；T表示算法的迭代次数；D表示求解问题的维度；Cobj表示目标函数的代价。

表3 不同算法的复杂度对比Tab.3 Complexity comparison of different algorithms

2.2 寻优结果

统计理论在群体智能优化算法性能分析中有着广泛的运用。为了验证选择的6 种优化算法的性能，针对同一基准函数独立寻优测试30 次。寻优结果的统计值包括：最优值（Best）、最差值（Worst）、平均值（Mean）、标准差（Standard deviation，STD）、寻优时间和中位数（Median），如表4～5 所示。表4～5 中：除寻优时间外，加粗字体综合考虑了对比算法的寻优性能；寻优时间仅考虑对比算法的搜索时间。

从表4 中可以看出，对于单峰测试函数F1～F5的寻优仿真，除函数F1和F3外，PO 算法的寻优结果均优于其他5 种群智能优化算法；对于F1和F3，SMA 虽然能和PO 算法达到同样的寻优值，但是寻优时间远远比PO 算法长，即SMA 的收敛速度差。

表4 基准测试函数寻优结果（单峰）Tab.4 Results of benchmark functions（unimodal）

从表5 中可以看出，针对测试函数F6的寻优，HHO 算法均优于其他5 种优化算法；针对测试函数F7的寻优，HHO 算法、PO 算法及SMA 能够达到同样的寻优精度，但SMA 的寻优时间最长，即收敛速度差；针对测试函数F8的寻优，除HBO 算法外，其他5 种优化算法均能达到最优的寻优值，EO算法的寻优时间较短，SMA 的寻优时间较长；针对测试函数F9和F10的寻优，PO 算法的寻优结果在6 种优化算法中最佳，此外，HBO 算法的寻优时间较短，但两个函数均没有达到最佳的寻优值。

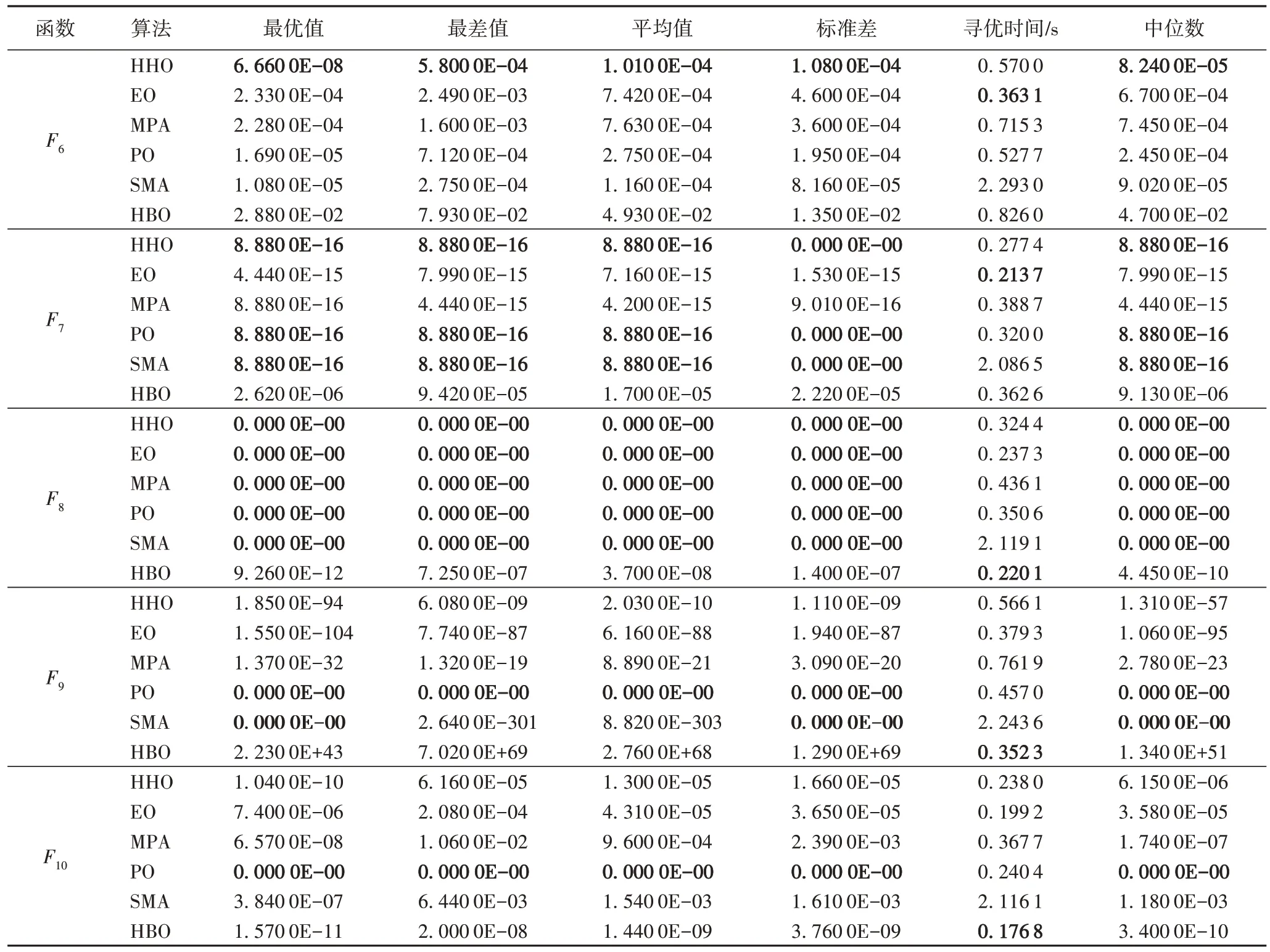
表5 基准测试函数寻优结果（多峰）Tab.5 Results of benchmark functions（multimodal）

为了说明6 种优化算法的收敛速度，对10 种测试函数的寻优过程曲线如图1～2 所示。图1（a）～（e）分别表示对比算法对5 种单峰测试函数的寻优曲线趋势；图2（a）～（e）分别表示对比算法对5 种多峰测试函数的寻优曲线趋势。横坐标表示对比算法的最大迭代次数，均为1 000；纵坐标表示对测试函数的寻优值的对数（lg）。

图1 六种算法的寻优曲线比较（单峰）Fig.1 Comparison of convergence curves of six algorithms（unimodal）

从图1 中可以看出，对于单峰函数F1～F5的寻优，除F4外，PO 算法分别在400 次、850 次、450 次和50 次迭代附近达到了理论最优值；而SMA 可以在800 次迭代附近搜索到函数F1和F3的理论最优值。从图2 中可以看出，PO 算法对函数F8和F10的寻优均在100 次迭代内达到理论最优值。对于F8的寻优，HHO 算法、EO 算法、MPA、PO 算法和SMA 均可以搜索到理论最优值；对于函数F9的寻优，SMA 和PO 算法均在800 次迭代达到了最优值。总的来说，从测试函数的统计结果和寻优收敛曲线均可以看出，PO 算法在6 种对比算法中的性能较佳，HBO 算法的寻优精度较低，可以进一步地改进研究。

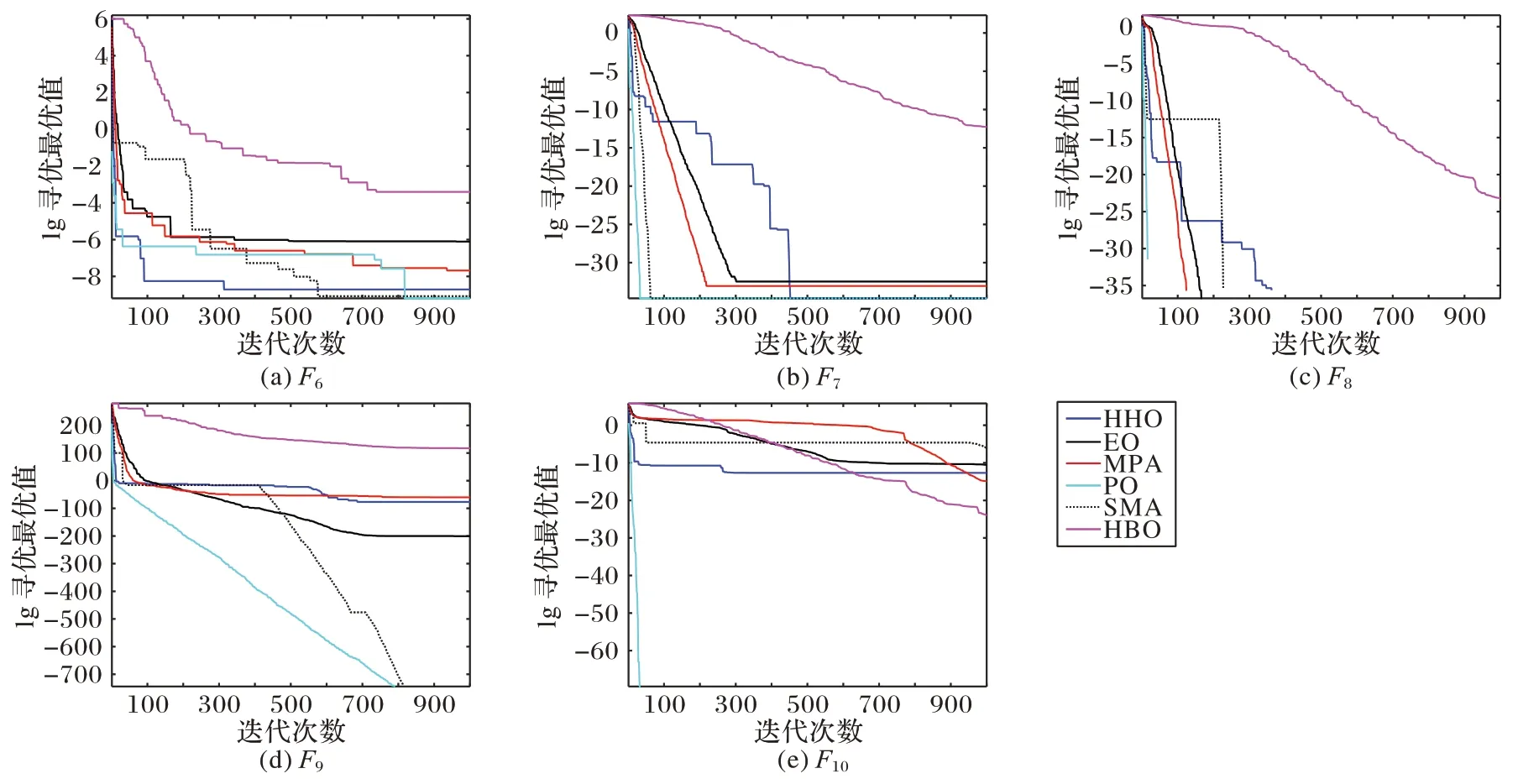
图2 六种算法的寻优曲线比较（多峰）Fig.2 Comparison of convergence curves of six algorithms（multimodal）

2.3 分析小结

从基准测试函数的仿真结果来看，PO 算法能够达到测试函数的理论最优值，且寻优时间较短，即PO 算法的寻优精度整体上优于其他5 种算法，且收敛速度较快，稳定性较好。针对10 种基准测试函数的寻优结果，在不考虑寻优时间的情况下，6 种优化算法进行排名：PO >SMA >HHO >EO >MPA >HBO；结合表3 的各个算法的计算复杂度来看，SMA的收敛速度较差，在确保寻优精度的前提下对SMA 进行改进。由于HBO 算法的寻优精度低，需要进一步地改进来增加寻优精度。

此外，各优化算法的理论性研究不足，需要从理论上对提出的算法进行收敛性分析［24］。对于优化算法的改进，建议如下：算法的种群可以采用混沌理论来提高其遍历性；控制参数同样可以运用混沌映射或非线性策略进行调节，提高算法的寻优性能；混合不同的优化算法优点来提高被改进算法的寻优精度等［25］。

3 工程约束问题的应用对比

为进一步分析6 种优化算法的性能，选择了工程中3 种非线性约束优化问题：工字梁设计问题、三杆桁架设计问题和减速器设计问题。这3 种工程优化问题的具体描述详见文献［2］。6 种算法的种群数量设置为25（其他参数设置详见表2）；迭代次数设为1 000；对求解每个工程约束优化问题分别独立运行30 次；并分析其寻优结果的统计值：最优值、最差值、平均值、标准差、寻优时间。

3.1 工字梁设计问题

工字梁设计问题［2］的目标是在承受最小的工字梁的垂直扰度，同时满足给定载荷下的截面面积和应力约束。当梁长L=200 cm，弹性模量H=2×104kN/cm2，最大弯曲力P=600 kN 和Q=50 kN 时，垂直挠度f（x）=PL3/48HI最小（单位为cm），其中：I为使用材料的截面惯矩（单位为cm4）。

该问题的目标函数及约束条件表述如下：

其中：决策变量（x1，x2，x3，x4）分别对应工字梁设计的上、下梁的宽度（b）、上梁和下梁底部之间的高度（h）、衔接梁的宽度（tw），以及上、下梁的厚度（tf）。各变量的取值范围为：10≤b≤50，10≤h≤80，0.9≤tw≤5，0.9≤tf≤5。

根据该问题的目标函数及约束条件，6 种算法的计算结果如表6～7 所示。

表6 工字梁设计的最优结果对比Tab.6 Comparison of best results of I-beam design

表7 工字梁设计的统计结果对比Tab.7 Comparison of the statistical results of I-beam design

对于工字梁设计问题，从表6～7 可知：6 种算法的均值（Mean）排名为：EO=MPA=SMA >HHO >PO >HBO；对应的标准差（STD）可以看出MPA 的稳定性优于EO 算法，EO 算法优于SMA；然而在寻优结果相近的情况下，EO 算法的寻优时间比MPA 和SMA 的寻优时间短。

3.2 三杆桁架设计问题

三杆桁架设计问题［2］的目标是在静压下桁架的体积应尽量减小，且满足每个桁架构件上受应力（σ）约束。该问题可转化为最佳横截面积（A1，A2）问题，其目标函数及约束条件表述如下：

针对三杆桁架设计问题的目标函数及约束条件，6 种算法的计算结果详见表8～9。

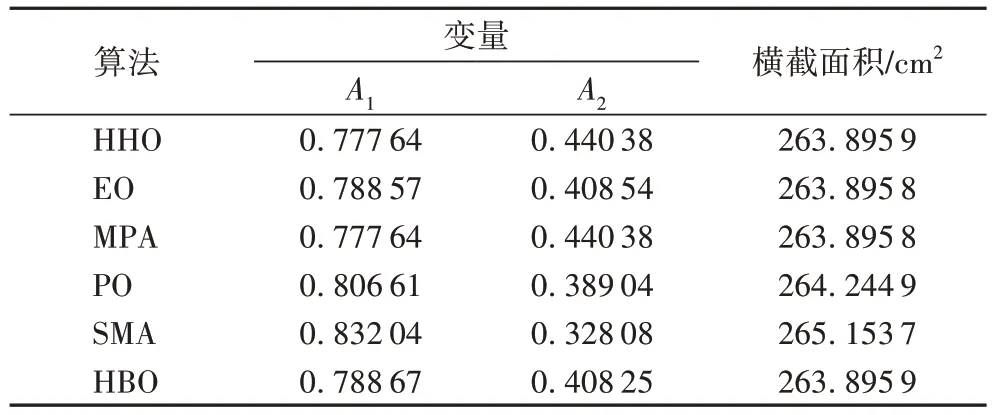
表8 三杆桁架设计的最优结果对比Tab.8 Comparison of best results of three-bar truss design

表9 三杆桁架设计的统计结果对比Tab.9 Comparison of the statistical results of three-bar truss design

对于三杆桁架设计问题，从表8～9 可知：6 种算法的均值（Mean）排名为：EO=MPA >HHO=HBO >PO >SMA；对应的标准差（STD）可得EO 算法的稳定性优于HBO 算法；然而HBO 算法的寻优时间比EO 算法的寻优时间短。

3.3 减速器设计问题

减速器设计问题［2］是典型的机械方面的优化问题，其目标是使减速器的总重量最小。该问题包括面的宽度（x1），齿的模量（x2），小齿轮上的齿数（x3），轴承之间的轴1 的长度（x4），轴承之间的轴2 的长度（x5），轴1 的直径（x6），轴2 的直径（x7）。约束条件主要有：齿轮齿的弯曲应力、表面应力、轴1 和2 的横向偏转传递的力、轴1 和2 之间的应力等。

该问题的目标函数及约束条件表述如下：

其中：2.6≤x1≤3.6，0.7≤x2≤0.8，17≤x3≤28，7.3≤x4≤8.3，7.8≤x5≤8.3，2.9≤x6≤3.9，5≤x7≤5.5。

针对减速器设计问题的目标函数及约束条件，6 种算法的计算结果如表10～11 所示。

表10 减速器设计的最优结果对比Tab.10 Comparison of best results of speed reducer design

表11 减速器设计的统计结果对比Tab.11 Comparison of the statistical results of speed reducer design

对于减速器设计问题，从表10～11 可知：6 种算法的均值（Mean）排名为：EO=MPA=HBO >SMA >PO >HHO；对应的标准差（STD）可以看出EO 的稳定性优于HBO 算法，EO 算法优于MPA；然而在寻优结果相近的情况下，HBO 算法的寻优时间比EO 算法和MPA 的寻优时间短。

4 结语

针对近两年来提出的6 种新型智能优化算法在求解工程约束问题上的应用：首先，基于对基准测试函数的仿真实验，分析了6 种算法的收敛速度、寻优精度和稳定性等性能；然后，将6 种算法用于求解3 种典型的非线性约束工程优化问题并分析性能。

基准测试函数的寻优结果表明：PO 算法的寻优精度整体上优于其他5 种算法，且收敛速度较快、稳定性较好；在不考虑寻优时间的情况下，6 种优化算法进行排名：PO>SMA>HHO>EO>MPA>HBO；结合各算法的计算复杂度和寻优的消耗时间，SMA 的收敛速度较差，在确保寻优精度的前提下对SMA 进行改进。由于HBO 算法的寻优精度低，需要进一步地改进来提升寻优精度；从寻优的结果来看，其他的算法亦存在收敛精度较低、收敛速度较慢、稳定性差等问题，因此需要进一步地改进研究。改进的方法可采用反向学习策略、非线性控制策略、混沌映射理论、混合算法等。从工程优化问题的求解来看，不同的优化算法对于不同的工程问题，其寻优的性能存在差异，即符合“No free lunch”理论［26］。

在未来的研究中，可以将收敛性能较好的算法应用于不同的实际问题，如：参数估计、特征选择与分类、非线性规划等工程问题；鉴于新型智能优化算法的理论性研究不足，需要进一步从理论上去分析和证明提出的智能优化算法的收敛性。