基于邻域熵的高光谱波段选择算法
翟东昌,陈红梅
(1.西南交通大学唐山研究院,河北唐山 063000;2.西南交通大学计算机与人工智能学院,成都 611756)
0 引言
随着遥感技术的发展,成像光谱仪发射的数百个连续窄波可以探测到地物目标丰富的光谱和空间信息,这些获取的信息经过成像处理后称为高光谱图像。近些年,高光谱图像广泛地应用到了多个领域,主要包括地质勘探[1]、农业[1-2],以及医疗行业[1-3]等。
高光谱图像包含了二维的空间信息,以及一维的光谱信息,所以高光谱图像的数据可以通过一个三维的图像立方体呈现。然而高精度传感器可以采集到高分辨率的空间信息,连续的数百个探测波段也使得图像中每个像素点都包含了大量的光谱信息。根据美国国家航空航天局(National Aeronautics and Space Administration,NASA)喷气推进实验室的数据,高光谱红外成像设备发送的平均数据量在65 Mb/s[4]。这使得数据处理过程中的时间成本增加,对硬件的要求也在提升,同时也会引发Hughes 现象[5]和Bellman 维度的诅咒[6]。
此外,高光谱图像从光谱信息的维度来看,可以将波段作为一个维度对空间信息进行描述,是不同波段探测灰度值的叠加。对于探测、分类等相关任务,要鉴别的物质只对部分波段进行吸收和折射,这使得光谱信息中包含了大量冗余、噪声信息,全波段在实际应用中的性能也较差。因此对高光谱数据集进行降维处理,降低数据间的冗余度,提高数据的可用性,是数据预处理中的重要环节。
对高光谱图像进行降维处理的方式主要包括了波段选择以及特征提取。特征提取按照算法中的标准将原始数据映射到另一个特征空间[7-8]。大部分特征提取算法将原始波段进行了线性组合,如果采用的算法指标不合适,可能导致计算结果更加复杂[9];波段选择算法,也称为特征选择算法,从原始波段中选取波段子集,并保留了光谱通道的原始光谱信息。
基于数据提供的不同的先验知识,研究学者提出了很多波段选择算法。根据是否采用数据的类标,波段选择算法通常可以分为三种:有监督的、半监督的和无监督的方法[10]。考虑是否采用分类器,波段选择算法还可以分为:包裹式方法,即采用可预测的模型及其泛化性能对特征进行排序[11];嵌入式方法,在模型构建的过程中选取最相关的特征[12];过滤式方法,通过引入其他评判标准来取代分类器准确率,对特征进行排序及筛选。
相较于包裹式算法,过滤式算法不用考虑分类器对特征选取的影响,所以通常会比包裹式算法更为高效,这使得此类算法在高维数据集中的性能会更好。要获取特征的相关性程度,常用的评判标准有基于皮尔森相关系数的方法[13];基于统计检验的方法,如t-检验[14];基于Fisher 线性判别的方法[15];基于最近邻类别的方法[16];基于互信息(Mutual Information,MI)的方法[17]等。
基于相关性系数的方法对线性特征非常有效,但是对于非线性特征之间的关系无法有效度量;基于统计检验的方法以及基于Fisher 线性判别的方法需要特征集合的数据服从正态分布;在Guo 等[18]的研究中,基于MI 的方法可以度量任意随机变量之间的信息量,所以适用于复杂分类任务中特征相关性的计算。此外,基于MI 的特征选择算法不依赖机器学习模型以及特定基准的选取。研究学者利用图像的空间信息[19],将样本像素值之间的极差作为权重方程,与MI 结合,其中极差之和可以作为另一种相似度的度量。或者在Liu 等[20]的研究中,将MI 与粗糙集理论相结合,采用MI 的思想计算邻域MI,并通过粗糙集理论的重要度进行波段选取工作。
本文引入了一种基于MI 的度量方式,称为邻域熵(Neighborhood Entropy,NE),用于度量多个特征之间的MI,并且克服了传统MI 方法需要一对特征变量进行计算的缺陷。此外,高光谱图像数据集的特征值为实数,近似搜索算法有效地减少了计算样本邻域集合耗费的时间。本文将两种算法结合在一起,提出了一种基于NE 的单次索引特征选择(Single indexed NE Feature Selection,SINEFS)算法,运用到高光谱图像的波段选择过程,并与其他常用的基于MI 的特征选择算法进行了对比分析。
1 MI理论及相关的特征选择算法
1.1 MI理论基础
本节将对基于MI 的特征选择算法进行说明,以下是信息熵相关内容的说明。
信息熵:对于一个分类任务,通过Pr(k)表示不同类出现的概率,其中k=1,2,…,N。熵是每种类度量不确定性的方式,计算公式如式(1)所示:

条件熵:对于一个分类任务,通过Dd来表示一个集合,元素为第d个特征所有可能的特征值,其中1≤d≤D;通过Dc来表示一个集合,元素为不同的类。在知道第d个特征后的平均不确定性称为条件熵,定义如式(2)所示:
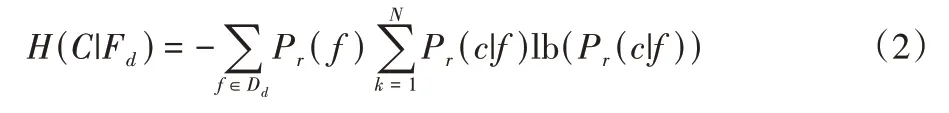
互信息:类C和一个特征Fd之间的互信息定义式为:
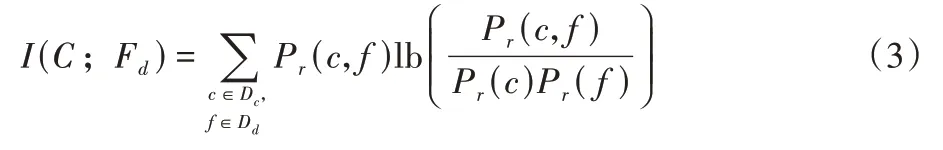
根据公式可知,条件熵往往小于或等于信息熵,当且仅当输出的类变量和特征是独立的随机变量时,条件熵等于信息熵。当特征Fd已知时,MI 相较于信息熵的值会减少。将式(3)推导后可得:
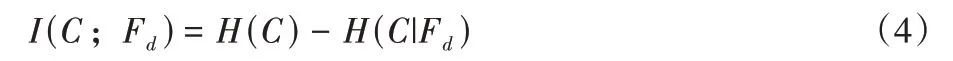
其中:C和Fd是对称的。根据Fano 不等式[20],MI 和一个学习系统的精度有相关性。以下是Fano 不等式的定理。
定理1Fano 不等式[21]794:设随机变量x和y分别代表一个噪声通道的输入和输出信息。一个接收器通过方程f(y),将收到的信息y重构成原始输入信息x,其中x*=f(y)。设E为二进制随机变量来表示一个事件是否为错误,即E=1 时,给定通道的输出y的解码结果x*和原始输入x不同,则不等式的表达式为:

其中:N是不同输入通道的个数。将y等价于一个特征Fd,x等价于类C,接收器中转化用的方程f(·)等价于一个用于分类的算法,则Pr(E=1)可以等价于一个分类器的误差率。根据式(5),Pr(E=1)的下界和条件熵H(C|Fd)成正比。因此,减少该值可以相当于在增大MI 的值,是降低误差率且构建有效分类器的必要条件。
1.2 基于MI的特征选择算法
接下来将对一些基于MI 进行特征选择的方法进行说明。基于MI 的特征选择算法是最大化相关性特征选择(Maximum Relevance-Mutual Information Feature Selection,MR-MIFS)算法,首先计算类变量和每个独立特征之间的MI值,然后对MI 值进行排序,选择最高的s个特征。但是此类算法在特征选择过程中容易将连续的特征进行选取,为了改进上述算法,在算法的评价机制中引入了最小化冗余度,以筛选所选特征之间较小相关性的特征。此类算法称为最小化冗余度以及最大化相关性的特征选择(minimum Redundancy MR-MIFS,mRMR-MIFS)算法[22]。该算法首先通过计算类变量之间的MI,将MI 作为相关性的评价标准,并选择相关性高的特征。然后在相关性较高特征集合里再计算冗余度,筛选冗余度较小的特征集合。在特征集合冗余度的计算中,也采用MI 进行对比,用于再次筛选。
通过计算已选特征以及未被选择特征之间的归一化互信息的特征选择算法,称为归一化互信息(Normalized Mutual Information,NMI)[23]。首先计算MI 作为选取特征的指标,再计算所选特征以及被选择特征之间MI 最小的值,特征之间的MI 值会被最小MI 值归一化处理。归一化后的MI值在0~1,当NMI 为0 时,说明两个特征之间完全独立;当NMI 值为1 时,说明特征之间的相关性较高,以此作为冗余度评价的标准,对波段子集进行筛选。
以上两种算法都是按照一对特征,或者特征和类之间的配对进行互信息值的计算。上述的相关性和冗余度需要分别计算。在文献[24]中提出的特征选择算法将MI 泛化到多个特征上,称为精准互信息特征选择(eXact Mutual Information Feature Selection,X-MIFS)。该算法计算所选特征的特征子集和类变量之间的MI,未被选取的特征和特征子集具有较高的相关性,才会选取该特征。从计算MI 的角度看,该算法在计算MI 的过程中不是两个一维向量之间的计算,而是一个一维向量和多维随机变量进行MI 的计算。
对于无监督的特征选择算法,MI 也是有效的特征评价标准。Martínez-Usó 等[25]提出的基于互信息的Ward连锁策略(Ward’s Linkage strategy using Mutual Information,WaLuMI),采用基于层次聚类结构算法将类似的特征分成不同的特征子集,使子集之内的方差最小、子集间的方差最大,通过MI实现这种度量方式,以减少波段间的数据冗余。
相较于上述的策略,本文提出的算法是一种通过最大化MI 的贪婪特征搜索过程。根据1.1 节的式(3),最大化MI,即最大化式(3),等价于最大化式(4)。在式(4)中,方程式的第一项H(C)是常量,在算法中可以忽视,最大化MI 只需要最小化方程式中的第二项条件熵H(C|Fd),其中1≤d≤D。对于高光谱图像,分类器应该将图像中某个光谱通道下像素值接近的点归为同一类,其中对于某一个类来说,在该光谱通道下条件熵的值应该是非常小。与之相对应,当一个类的在某个光谱通道下的条件熵非常高,对于分类任务而言该通道的光谱信息是冗余的,甚至是噪声信息。所以可以将类相较于一个特征的条件熵作为评价特征和类相关性程度的指标,用于选取最富有信息量的波段。
2 本文算法
2.1 邻域熵
由式(2)可知,计算类和特征之间的条件熵,需要知道Pr(f)和Pr(c|f)的概率分布。本文采用了基于NE 的计算方法可以不需要估计类熵相较于一个特征的概率分布,只用考虑一个样本点的邻域范围的类,并给数据集中的所有样本点求平均。NE[26]是信息熵在数字特征上的泛化,接下来详细介绍相关内容。
给定一个分类任务,其中S是一个多维随机变量,X是S的一个实例。δ(X,k)是X及其k个最近邻域样本(k-Nearest Neighborhoods,k-NN)的集合,则对于一个类c∈Dc,其邻域集合δ(X,k)的相对频率为:
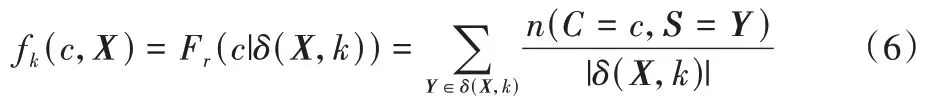
其中:|·|为集合的基数;n为一个事件发生的次数。则类变量C相较于S的NE 可以定义为:
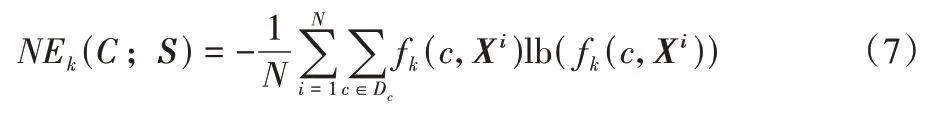
其中:Xi代表了S的第i个实例。根据式(3)和式(4),通过最小化NE,也就是最大化MI,因为条件熵式(2)和NE 可以推导出近似关系[26]22:

对于特定波段的NE 以及MI,NE 可以不需要估计特征的概率分布以最大化MI,并且NE 采用了自适应的不确定性计算方式,只需要计算一个样本点邻域内类变量及相关频率。
算法执行主要的时间都消耗在样本点最近邻的搜索过程中。如果已经选取了i个波段,在第i+1 次循环过程中,NE特征选择(NE Feature Selection,NEFS)算法为寻找s个波段的CPU 时间复杂度为O(CDs)。
在算法执行的过程中,考虑到高光谱图像的样本点个数和其空间分辨率相关,所以算法构建过程中样本邻域的搜索是一个重要的环节。本文提出的算法中采取了局部敏感哈希(Local Sensitive Hashing,LSH)算法搜索邻域集合。LSH算法接受一定程度下近似带来的误差,搜索速度会远高于基于度量距离的暴力搜索方法。
2.2 LSH算法
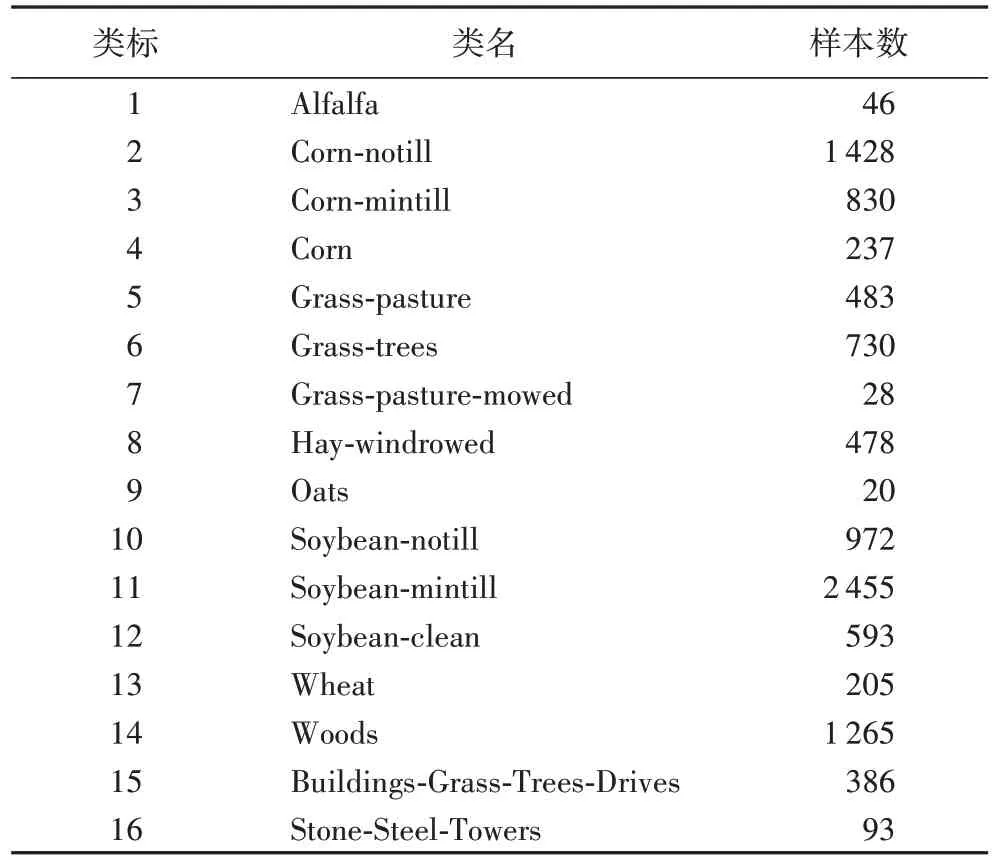
对于高光谱图像数据集,假设其包含D个波段,N个样本点,数据集往往符合D 在本文中,主要采用的方法是Gionis 等[27]提出的搜索算法。通过索引技术将样本点分到不同的组,每个组的样本点是近似邻阈值。在查询阶段,索引可以帮助样本点到相应的组内,从而再计算组内样本点之间的距离。以下是对LSH 搜索算法的说明。 设dist 为D个波段的高光谱数据集M中任意两个样本点之间的距离计算公式。对于任意样本点P,通过dist 计算距离,令B(P;r)表示距离P的范围r内的所有点的集合。 LSH 方程[27]522:对于一个哈希方程簇H,方程h(·)对距离公式dist 具有(r1,r2,p1,p2)敏感性,其中r1 如果P∈B(Q;r1),则PrH(h(Q)=h(P))≥p1; 如果P∉B(Q;r2),则PrH(h(Q)=h(P))≤p1。 在NEFS 中,LSH 需要由适用于欧氏空间的局部敏感哈希方程簇来实现,这些方程定义为: 其中:w是一个固定的正整数;b是从[0,w]中随机获取的数。为了计算范式l2的距离,从高斯分布中获取a∈RD。 在NEFS 每次运算的过程中,波段和类之间的NE 需要构建一个新的LSH 索引,时间复杂度为O(Ds)。L个新的哈希方程在NEFS 每次循环中会构建一次,对于每个方程,需要生成b以及向量a∈RD,这些相当于系数的生成过程,时间复杂度为O(Ls2)。当选取的波段子集基数变化时,需要用式(9)将数据集中的每个点哈希L次。循环过程中总共需要构建Ds次索引,因此对于i=0,1,…,s-1,需要哈希的值的个数为NL,则时间复杂度为O(NLDs2)。构建索引后,每个样本点的NN 搜索会计算样本点的哈希值,然后在L个哈希表中找到候选的样本点,最后从候选的点集合中使用距离度量的方式找到邻域子集。查询一个样本点的时间复杂度为O(DNL(1+ε))。因此计算NE 过程中所有波段子集的时间复杂度为O(DN(2+ε)/(1+ε)s2),令α=(2+ε)/(1+ε),则本文提出的NEFS 算法的时间复杂度为: 本文算法indexed-NEFS 将LSH 算法和NE 计算的过程结合在一起,并且在LSH 构建流程中进行了优化。在2.2 节中提到,LSH 构建索引的过程中,需要当前用于计算NE 的波段子集构建索引,但是本文在D维数据集上只构建了一次索引,也就是在全特征下构建了一次。当NE 子集进行计算时,第一个过程就是获取一个样本点的全特征索引,然后在样本点的哈希表中搜索NN 个样本点。这是基于以下两点考虑的:首先,对于D维数据集,利用数据表达的空间信息,样本点的邻域集合在全特征的情况下,也是特征子集s样本点的邻域集合,其中s 为了评估提出算法的性能,本节将详细阐述高光谱波段选择的实验结果。首先简单说明实验中采用的两个高光谱图像数据集:Indian Pines 和Salinas。 Indian Pines 数据集从普渡大学多光谱图像数据分析小组的站点下载。该数据集为NASA 在1992 年6 月12 日采用JPL 的机载可见/红外成像光谱仪传感器采集,它具有每像素20 m 的空间分辨率和10 nm 光谱分辨率,涵盖光谱0.4 μm~2.5 μm。本文实验中的数据集为此次采集的一张较大图像的子集,由145×145 个像素,224 个光谱反射带组成,图1 为Indian Pines 数据集的三通道图像。 图1 Indian Pines 三通道图像Fig.1 Three-channel image in Indian Pines 通过移除受水汽影响以及噪声波段对应的数据,实验中采用的Indian Pines 数据集的波段个数为200(移除104~108、150~163 以及220 波段)。数据集各个类标样本量的详细信息如表1 所示,地物信息主要包括了蔬菜、植被以及公路铁路。 表1 Indian Pines数据集的类标以及相应的样本数Tab.1 Class labels and corresponding numbers of samples in Indian Pines dataset Salinas 数据集从加利福尼亚州Salinas 山谷上空采集,传感器为AVIRIS,包含了224 个波段,具有高空间分辨率(每像素3.7 m)的特征以及512×217 个像素点。和Indian Pines 数据集一样,移除了20 个吸水的波段以及噪声波段(移除108~112、154~167 以及224 波段)。图2 为Salinas 数据集的三通道图像。 图2 Salinas数据集的三通道图像Fig.2 Three-channel image in Salinas dataset 数据集各个类标样本量的详细信息如表2 所示,地物信息主要包括了蔬菜、土壤以及葡萄园。 表2 Salinas数据集的类标以及相应的样本数Tab.2 Class labels and corresponding numbers of samples in Salinas dataset 本文提出的算法将与其他基于MI 的特征选择算法进行波段选择实验进行比对,其中包括1.2 节提及的mRMRMIFS、NMI、X-MIFS 以及WaLuMI。 算法执行效率将通过时间复杂度的分析以及算法CPU时间进行对比,以评价LSH 对邻域集合搜索效率带来的提升。并通过分类实验体现SINEFS 算法的可靠性以及有效性。 在本文的实验中,最佳的波段个数是不确定的,不同数据集上最优的波段个数也会存在差异,所以各个算法选择的波段个数范围从5 到60,以等步长5 依次增加。 完成波段选择算法后,将采用分类任务对选取波段的有效性进行评价。主要采用的分类器为支持向量机(Support Vector Machine,SVM)、径向基核函数(Radial Basis Function,RBF)、随机森林(Random Forest,RF)分类器进行分类,其中RF 树个数设置为20。通过分类器计算获取各个特征作用下,分类的总体精度(Overall Accuracy,OA)和Kappa 系数(Kappa Coefficience,KC)。此外,为了使分类结果的可信度提升,进行10 次十折交叉验证,对于每种特征选择算法,分类实验中分别在两个数据集随机划分样本集合作为训练集和测试集,并将OA 和KC 的均值作为结果进行比对。 所有算法在8 核64 位,CPU 频率在2.6 GHz,内存16 GB的计算机上运行。算法通过Python3 实现,所有算法在实现过程中没有利用语言特性或者相关张量计算库提升运算性能,算法按照伪代码的实现步骤进行编写,以保证所有实验结果的有效性。实验中的分类器采用第三方库sklearn 提供的SVM 和RF,以获取有效的OA 和KC 进行实验结果比对。 为了有效地比对各个算法的时间复杂度,如3.2 节说明的,对选择特征值的个数进行设置。虽然从时间复杂度进行分析所选波段的个数只是部分影响因素,但是算法在实际运行过程中,选择特征的个数对执行效率影响较大。 对于mRMR-MIFS,算法计算相关性的时间和样本数量为线性关系,且为正相关。随着搜索样本数量的增加,算法执行的时间也会增加。算法计算相关性最差的情况是O(N)。算法循环的过程中,需要执行O(|S|)次计算以获取特征之间的相关性,并更新特征子集中最大相关性的值。该算法的时间复杂度为CmRMR-MIFS=O(DNs2)。 NMI 算法在执行过程中需要对计算出来的特征对进行排序,排序算法采用堆排序,时间复杂度为O(NlogN),其中N为样本个数。考虑已选择的特征个数s,NMI 的时间复杂度为CNMI=O(DNslogN)。 X-MIFS 算法和NEFS 的贪婪搜索过程一致,不同之处在于评价指标为MI,NEFS 为NE。在计算MI 的过程中需要用到修改的式(3),将其中的概率分布函数用多维直方图的预估器进行替换。在X-MIFS 实现的过程中需要对特征二进制化,所以对于每个子集,通过对所有点的线性遍历来估计联合概率分布和边际概率分布。因此选择s个特征的时间复杂度为CX-MIFS=O(DNs2)。 WaLuMI 算法在执行过程中主要包括两个部分。首先是聚类部分,对于一个型为L×L的距离矩阵,以及特征个数为D的数据集,聚类部分的时间复杂度为O(L2D)。第二部分进行离散的子集MI 计算。该计算部分和聚类后的特征子集个数,以及MI 计算过程相关,时间复杂度为O(LDN)。所以WaLuMI 的时间复杂度为O(LDN+L2D)。表3 显示了各类算法的时间复杂度。 表3 各个算法的时间复杂度Tab.3 Time complexity of each algorithm 为了能够测试各类算法运行的效率,在表4 中显示了用CPU 的时间模型,数据集固定在DN,s为10,L为N的1/4,ε=15,各类算法运行时间的最小二乘法线性模型。 表4 CPU时间线性模型Tab.4 CPU time linear model 结合3.2 节NEFS 的时间复杂度分析结果可知,NEFS 在各类算法的比对中较慢,因为会消耗大量时间进行索引构建以及NNs 的搜索。SINEFS 在引入单次构建LSH 索引后,α≈1,即执行效率会接近NMI,相较于NEFS 效率有显著的提升;mRMR-MIFS、WaLuMI 和X-MIFS 是速度较快的算法,其中X-MIFS 运用了二进制特征,使得其执行效率较高。当WaLuMI 设置距离矩阵L较大,以及数据集特征数量多时,执行消耗会增加。 3.4.1 Indian Pines数据集实验结果 本节分析并比对各类算法在Indian Pines 数据集上的实验结果。图3 显示了各个算法选取的波段子集,以及全波段集合,采用SVM 以及RF 进行分类的OA 值。 当分类器选取SVM 时,由图3(a)可知,全波段OA 为77.56%,选取波段个数小于20 时,除了SINEFS,其他算法选取的波段OA 低于全波段OA;当波段子集数为40 时,WaLuMI 选取的波段子集OA 超过了其他算法选取的波段子集,且OA 超过了SINEFS;当选取波段个数超过50 时,X-MIFS 的OA 超过了全波段OA;mRMR-MIFS 和NMI 的性能较差,选择的波段子集均未超过全波段OA。WaLuMI 在60个波段子集时OA 达到了最优,为83.90%。根据实验结果,SINEFS 选取的波段子集,能够较快地超过全波段OA。 当分类器选取RF 时,根据图3(b),除了NMI 在5 个选取波段的OA 值,其他算法OA 的整体结果优于SVM。其中全波段OA 为79.80%。当波段子集数为30 时,SINEFS、WaLuMI 以及X-MIFS 的OA 值优于全波段OA。在波段子集数为35 和40 时,SINEFS 的OA 值分别为84.45%和84.85%,WaLuMI 的OA 值分别为84.62%和84.71%。虽然SINEFS 在波段子集数为40 时OA 最高,但是在这个区间的OA 结果两种算法差别不明显。 图3 Indian Pines数据集上采用SVM以及RF进行分类实验的OA值Fig.3 OA values of classification experiments using SVM and RF on Indian Pines dataset 图4 显示了各个算法选取不同波段子集,以及全波段集合,采用SVM 和RF 进行分类的KC 值。 图4 Indian Pines数据集上采用SVM以及RF进行分类实验的KC值Fig.4 KC values of classification experiments using SVM and RF on Indian Pines dataset 从图4(a)的KC 值来看,当选取波段子集为15 时,SINEFS 的KC 为0.736 6,优于全波段以及其他算法的KC值;WaLuMI 和X-MIFS 在40 个波段子集时超过了全波段KC。当SINEFS 选取波段子集为55 时,KC 为最高的0.797 6。其他算法在RF 分类器的分类结果相较于SVM 呈现上升趋势,在高于55 个波段子集时,除了WaLuMI,KC 值有一定的回落。 从图4(b)的KC 值分析,全波段KC 值为0.754 6,SINEFS 在30 个波段子集超过了全波段KC 值,为0.772 4,同样为所有算法中最快超过全波段的算法。SINEFS 和X-MIFS随着波段子集的增加,KC 值也在增加,在波段个数为55 时,达到最优0.837 5。在波段个数为60 时,SINEFS 的KC 值有回落,但是依然高于其他算法以及全波段KC 值。 3.4.2 Salinas数据集实验结果 在本节,分析并比对各类算法在Salinas 数据集上的实验结果。图5 显示了各个算法选取的波段子集,以及全波段集合,采用SVM 以及RF 进行分类的OA 值。对比图3 和图5 可以看出,在Salinas 数据集上,两种分类器获取的OA 值均高于Indian Pines 数据。 图5 在Salinas数据集上采用SVM以及RF进行分类实验的OA值Fig.5 OA values of classification experiments using SVM and RF on Salinas dataset 当分类器选取SVM 时,根据图5(a),全波段OA 值为77.56%。SINEFS 和WaLuMI 在10 个波段子集时OA 值分别为77.32%和77.88%,OA 值较为接近,WaLuMI 先超过了全波段OA 值。在波段子集数为15 时,SINEFS 的OA 值超过全波段OA 值,为79.71%。其他算法OA 值均随着波段子集的个数增加,逐渐超过全波段OA 值。在选取40 个波段子集时,SINEFS 超过WaLuMI 达到最高OA 值,为92.99%。波段子集数范围在25~55 时,SINEFS 的OA 值优于WaLuMI 及其他算法,在60 个波段子集,SINEFS 的OA 值回落,WaLuMI 有小幅度增加。 当分类器选取RF 时,根据图5(b),SINEFS 为OA 值增加最快的算法,当选取10 个波段时,OA 值为80.70%,高于全波段的79.80%。波段子集区间10~40 时,SINEFS 高于其他算法。但是在45 个波段时,WaLuMI 达到了最佳OA,值为93.43%,SINEFS 的OA 值开始小幅度下降。其他算法在波段数位25 时均超过全波段OA,并在后面的特征集合中呈上升趋势。 图6 显示了各类算法在Salinas 数据集上KC 值的实验结果。相较于图4 中显示的结果,在Salinas 数据集上KC 值整体优于Indian Pines 数据集。 图6 Salinas数据集上采用SVM以及RF进行分类实验的KC值Fig.6 KC values of classification experiments using SVM and RF on Salinas dataset 根据图6(a),SINEFS 在20 个波段子集时超过全波段KC 值,其中SINEFS 为0.755 3,全波段KC 为0.734。波段子集数范围在30~40 时,WaLuMI 的KC 值优于SINEFS 及其他算法,但是SINEFS 在所有波段区间都保持了增长的趋势,而WaluMI 出现了回落。mRMR-NEFS、NMI、X-MIFS 在整个效果上优于Indian Pines 数据集,且在波段子集数为35 时,均超过了全波段的KC 值。 根据图6(b),SINEFS 在10 个波段的KC 值超过了全波段KC 值,分别为0.775 5 和0.754 6。波段数在5~40 时,SINEFS 的KC 值均优于其他算法,在波段数为30 时,SINEFS的KC 达到最大值0.860 8。WaLuMI 的KC 值在波段数为45时达到实验最佳,为0.872 2。其他算法KC 值均优于Indian Pines 数据集,且在波段数为30 及以上,均超过了全波段的KC 值。 本文根据MI 理论,提出了一种基于MI 波段选择算法,该算法通过最小化NE,同时最大化特征和输出变量之间的MI。该算法采取了贪婪的搜索策略,以及LSH 优化NNs 的搜索过程,以获取最优的波段子集。本文通过实验比对其他基于MI 的特征选择算法,实验结果显示,相较于其他比对算法,本文提出的SINEFS 可以更快地达到较优的波段子集,能在较小的波段集合的区间获取较优的分类效果;但是本文的邻域搜索过程中LSH 的参数设定为人为设定,随着数据集的变化,需要预先计算以获取最优参数,后续需要采用其他技术进行优化,以适用于更多的工作场景。
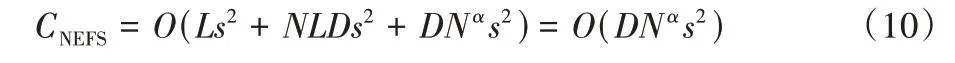
2.3 SINEFS


3 实验与结果分析
3.1 实验数据集



3.2 实验设计
3.3 时间复杂度分析


3.4 分类实验结果与分析




4 结语

