基于小样本无梯度学习的卷积结构预训练模型性能优化方法

李亚鸣，邢 凯*，邓洪武，王志勇，胡 璇

（1.中国科学技术大学计算机科学与技术学院，合肥 230027；2.中国科学技术大学苏州高等研究院，江苏苏州 215123）

0 引言

随着深度学习的发展和计算硬件设备的改进，作为深度学习代表性网络结构之一的卷积神经网络（Convolutional Neural Network，CNN）在图像识别和音频处理方面取得了快速发展并得到了广泛应用。卷积结构神经网络具有表征学习能力，能够以相对较少的参数量快速有效地提取图片和音频数据中的特征信息，避免了传统算法中复杂的特征预处理过程。近年来出现的卷积结构的深度学习预训练模型如ResNeXt［1］、DenseNet［2］在一些大型图像数据集上的性能表现已大幅优于传统的图像识别模型。

尽管基于卷积结构的深度学习预训练模型已经在图像处理领域现有数据集上取得了优异性能，但其在泛化性上仍面临挑战。首先，在实际生活中，大型数据集的获取往往需要消耗大量的人力财力，在许多场景下难以满足模型对数据规模的需求。其次，卷积神经网络模型通常是基于反向传播以及梯度下降进行学习的，随着网络层次越来越深，在优化的过程中，容易出现训练结果收敛于局部最小值而非全局最小值的情况。Zhang 等［3］指出基于梯度下降的方法通常需要高昂的花销对超参数进行调整才能达到模型性能的提升，并且作为反向传播的提出者，他认为反向传播可能并非大脑自然存在的机制［4］，并不一定是深度学习未来的方向。另外由于权重共享，卷积结构对局部数据采样构建局部特征，高层组合局部采样点构建高维抽象特征，容易出现对局部敏感，而对全局不敏感的情况，并且其普遍采用的池化过程中会丢失部分有价值的信息，导致进一步忽略局部信息与整体信息之间的相关性［5］。上述的这些问题限制了卷积神经网络性能的进一步提升。

针对上述问题，研究者们提出了多种解决思路对模型进行改进。针对梯度下降算法所存在的问题，Adam［6］、AdaGrad［7］等算法引入二阶动量，积累之前状态的动量替代梯度，实现了自适应学习率，加快了前期收敛，但也存在训练后期学习率震荡、模型无法收敛，以及过早停止训练导致泛化性差等问题。参数初始化［8］和中间层标准化策略［9］等方法对于深度学习模型性能提升相对有限，残差连接［10］和ReZero［11］等方法则通过增加跳跃式传递结构的方式让低层信号直接传递到高层，增强了梯度的反向传播，加快了模型优化的收敛。Swish 激活函数［12］和Mish 激活函数［13］则通过设计更平滑的激活函数替代ReLU（Rectified Linear Unit）激活函数，在复杂度增加很小的情况下提高了模型的稳定性以及准确性，平均性能更优。但这些方法仍然无法解决梯度下降的根本问题，模型的性能仍然受到限制。

针对模型训练过程对数据集规模的要求，目前的研究主要是进行数据增强处理，或是利用元学习，或是对模型添加先验信息的方式，以此来从较少样本中学习到较好的模型。这些方法都在一定程度上解决了数据量不足导致模型泛化能力差的问题，但仍然对先验信息提出了一定要求，对于小样本数据仍然面临较大挑战。

针对卷积结构以及池化层的缺陷，文献［14］提出基于本地重要性的池化（Local Importance-based Pooling，LIP）方法，采用注意力机制来自适应地保留下采样中的重要信息，贡献较小的信息则被过滤掉。文献［15］提出一种基于感兴趣区域的池化（Region of Interest pooling，RoI pooling）方法，选择对不同大小的区域进行池化，能够在一定程度上增加核心区域信息的关联程度，更好地提取有效信息。这些方法能够一定程度提升模型性能，但没有解决池化层存在的问题，仍会丢失部分有价值的信息。

另外，卷积神经网络中卷积层在提取信息的过程中往往存在特征提取冗余的问题，网络权重的相关性过高，导致模型泛化性下降［16］。当数据集质量较差时，卷积层的输出结果中将包含部分与样本核心语义无关的噪声信息，这些噪声信息将不仅会影响模型提取特征信息的质量，导致模型性能变差，还会消耗过多的算力。因此，如何准确评估采样点提取特征的有效性，筛选出没有贡献的噪声信息，也成为提高卷积神经网络模型性能的关键。

在本工作中，提出一种基于资本资产定价模型（Capital Asset Pricing Model，CAPM）［17］以及小样本数据来定向生成网络有效结构的方法，基于最优传输理论以及时不变稳定性对模型中间输出结果进行去噪，并以自监督的方式进行无需梯度下降和反向传播的表征学习，避免了梯度下降算法带来的缺陷，能够生成各个类别有效信息的类别感知表征向量，减少了传统方法中池化层带来的信息损失，并基于自注意力机制生成最终的表征嵌入向量。

本文的主要工作如下：

1）针对卷积结构预训练模型，基于资本资产定价模型来定向组合生成网络有效结构，基于时不变稳定性和自监督的方式，无需梯度下降和反向传播来进行表征学习，避免了对梯度的依赖；

2）基于小样本数据，利用数据增强技术生成调制序列数据，通过协整检验分析因果关系并据此定向修剪网络结构；

3）理论和实验分析表明，本文方法可应用于多类卷积结构预训练模型，对数据集规模的要求有数量级下降，同时模型性能和泛化性有明显提高。

1 相关工作

1.1 基于卷积结构深度学习模型的图像识别方法

早期的卷积神经网络发展并不顺利，文献［18］提出的LeNet-5 采用反向传播算法对模型进行优化，具备卷积层、池化层和全连接层三种基本模块，在数字识别任务上取得了一定效果，但在一般实际任务中的表现不如支持向量机（Support Vector Machine，SVM）、Boosting 等算法。直到AlexNet［19］的提出证明了卷积神经网络在大规模图像数据集上的可行性，使用ReLU 激活函数，证明其效果在深层结构中超过Sigmoid 激活函数，并首次将Dropout［20］以及LRN（Local Response Normalization）等技术应用到卷积神经网络中，增强了模型的泛化性。同时AlexNet 采用GPU（Graphics Processing Unit）进行运算加速。后续提出的VGGNet［21］对卷积核以及最大池化层作了改进，构建了更深的网络结构，证明了增加隐藏层深度以及小卷积核能够有效提高卷积神经网络的性能，但随着网络深度的增加，模型性能会出现先升后降的网络退化现象。在MobileNet V2［22］中提到激活函数ReLU 使得模型在输入输出过程中，由于信息不可逆，导致部分信息损失，模型中大量隐藏神经元对不同输入输出相同值，导致权重矩阵的秩较小，深层网络中矩阵连乘使得模型出现梯度消失问题。ResNet［10］提出残差连接结构，将模型深度提高到152 层，性能得到大幅提升，获得ILSVRC（ImageNet Large Scale Visual Recognition Challenge）2015 比赛分类任务的冠军。

ImageNet 2012 数据上训练得到的预训练模型在其验证集上取得了很好的效果，但仍然有性能优化空间。传统卷积神经网络方法一般只采用图片顶层特征做预测，因为顶层的特征语义信息较为丰富。顶层特征中目标位置比较粗略，而底层的特征语义信息较少，但是目标位置比较准确，所以有些算法采用多尺度特征融合的方式，利用融合后的特征做预测。在特征金字塔（Feature Pyramid Network，FPN）［23］中预测是在不同特征层独立进行的，将高层与底层的特征信息进行融合，得到了信息更丰富的融合特征并进行预测，模型性能得到提升。PyNET［24］中则采用了金字塔的思想，结合全局信息以及底层信息，低尺度得到的信息被上采样，然后和高层次的特征连接到一起，然后继续处理，结合了局部与全局的信息。这些方法都增加了新的采样方式，能够从样本中提取更多的有效信息。

1.2 资本资产定价模型

在网络模型中，不同神经元能够提取不同含义的信息，本文引入CAPM，将有价值的特征语义信息作为资产，然后对信息进行取舍组合，实现收益最大化。CAPM 是一种基于风险资产期望收益均衡基础上的预测模型，其核心思想是理性的投资者将选择并持有有效的投资组合，即那些在给定期望回报率的水平上使风险最小化的投资组合［25］。

如图1 所示，不同股票组合构成了组合可行区域，有着不同的收益以及标准差，资本市场线与组合可行区域上沿相切，切点P为理论上的最佳市场组合，达到风险与收益的平衡，相较于同样风险的M组合，P组合具有更高的收益率。构建有风险的投资组合时，一般的策略是投资回报达到无风险投资的回报，或者更多。

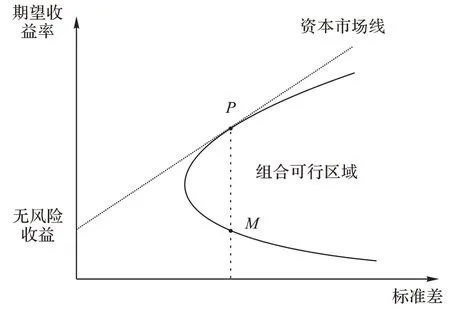
图1 资本资产定价模型Fig.1 Capital Asset Pricing Model

1.3 模型的不变性与Wasserstein度量

1.3.1 模型的不变性

图像识别任务中模型的不变性指的是样本经过各种几何变换，其核心语义信息不发生变化，模型仍然能将其够映射到原始样本对应的类别。对经过变换的样本图片具有一致的表达，是使得模型具备泛化性的重要保证。常见的有平移不变性、尺度不变性、旋转不变性等，一般通过不同的数据增强规则或者特定的网络结构使得模型具备对应的能力。卷积神经网络中的卷积层以及池化层一定程度上为模型提供了平移不变性，目标出现在样本的任何区域，卷积层都能够提取特征信息，输出同样的响应，而最大池化层中，即使最大值在感受野内出现了移动，仍然能够返回最大值。而在SPP-Net［26］中，引入SPP（Spatial Pyramid Pooling）层，通过SPP层来解除了卷积神经网络对于固定尺寸图片输入的限制，并采用多尺度训练方法，使用不同尺寸的样本图片进行训练，为不同尺寸的图片增强了模型的尺度不变性。对于旋转不变性等，卷积神经网络并没有加入对应的先验特性，需要大量的增强数据进行训练。

1.3.2 最优传输理论及Wasserstein度量

最优传输研究的是两个分部之间变换的问题，最早是对土堆搬运问题的研究，后来被抽象为给定两个度量空间D、G以及对应的分布α、ν，寻找最优传输变换G=T（D），将服从分布α的随机变量转换为服从分布ν，并最小化消耗函数［27］。最优传输问题为非凸优化问题，其解的存在性难以保证，后被松弛为线性问题，使得最优传输理论得到快速发展［28-29］。

Wasserstein 距离（简称W 距离）是一种在两个概率测度空间中近似寻找最优传输距离的方法。相较于JS（Jenson’s Shannon）散度，W 距离在两个概率分布的支撑集没有重叠或重叠较少的情况下，仍然能够反映出两个分布的远近，并且它值域不限制在0 到1，不存在上下限，能够很好地定义为资产定价模型中的收益。两个分布之间的W 距离定义如下：

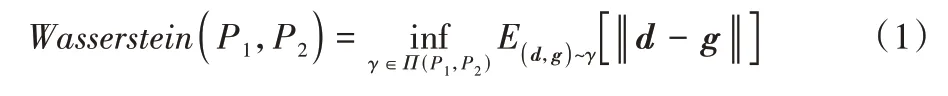
其中：Π（P1，P2）表示所有以P1和P2为边缘分布构成的联合分布γ（d，g）的集合；γ（d，g）表示将分布P1转换为P2需要从d传输到g的传输量，可以看作最优传输中的消耗量［30］。

2 基于调制序列的卷积网络结构定向修剪

2.1 基于小样本的调制序列数据生成

从大规模数据中找到有意义的关系能够有效提高神经网络的性能，目前主流的研究都是将神经网络看作黑盒，利用海量数据穷举获得相关性关系，而因果关系能够更好地解释神经网络的机制［31］。在因果推理中，因和果具有先后顺序性，因此通过观察时序数据能够更好地发现因果关系，但小样本数据属于非时序数据，因此本文基于干预调制的方法，利用现有的数据增强技术对小样本数据进行扩充，生成序列数据。文献［32］指出当对样本进行干预处理时，同时也限制了样本随其他因子变化的自然趋势，改变了原始数据的分布，不同的干预方式将导致完全不同的相关性关系，可以观察模型对于经过指定干预方式生成的样本所作出的响应。

因此本研究首先制定数据增强规则f对样本数据进行扩充：

其中：x为单个样本；y为经过变换后的增强样本；t为从调制曲线上采样得到的连续性变换参数，用于生成具有时间连续性的图片变换参数序列，以高斯模糊、移动观测窗口等变换方式对数据集中所有的样本都进行变换处理，参数则分别对应于高斯方差大小以及窗口坐标；ε为随机扰动项，能够避免采样的重复性，增强数据分布的鲁棒性、多样性。

考虑K个类别的数据集，每个类别中包含n个样本，基于具有时间连续性的参数以对同一类别中的每一个样本进行同样的m次连续性的数据增强，生成了大小为n×m的增强样本矩阵。即每个类别的原始样本都生成m组长度为n的时间样本序列，每一组都包含由n个原始样本基于同一参数进行变换处理得到的n个增强样本。同时也构成了n组长度为m的空间样本序列，每一组都包含由其中一个样本基于不同参数进行变换处理得到的m个增强样本，如图2 所示。基于调制曲线生成具有时间连续性的噪声能够对原模型造成更明显的扰动，对特征不变性的研究更有利。

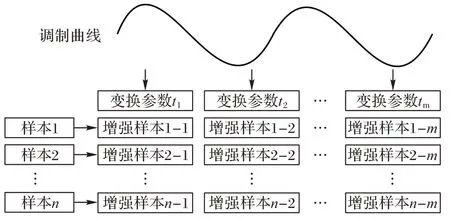
图2 样本数据增强Fig.2 Sample data augmentation

2.2 基于协整检验的卷积网络结构定向修剪

文献［33］指出一个经过初始化的神经网络模型，当数据变化时，其损失函数相较于输入数据的雅可比矩阵通过平展处理可看作一个向量，在不同类别的数据之间，性能越好的结构，对应的雅可比矩阵也将越不具有相关性，因此可以不需要对模型进行训练就能快速评估网络结构的好坏。类似地，对于采样点而言，其数据分布越平稳，与其他分布的重叠越少，则其采样质量将越高。如2.1 节所阐述的，基于调制曲线生成的增强样本对原始数据集进行了扩充，形成了时间样本序列。对时间序列而言，如果均值没有系统的变化（无趋势），方差也没有系统变化，且严格消除了周期性变化，就称之是平稳的［34］。因此首先考虑从时间序列平稳角度基于增强的样本数据对每个采样点稳定提取特征的能力进行评估，继而对预训练模型网络结构进行修剪。

为了评估不同采样点稳定提取特征的能力，本文采用W距离对不同数据分布进行度量。对于同一采样点，从时间角度看，其输出构成一个时间序列，序列中的每一组数据都可以看作一个数据分布，因此可以计算相邻时刻两个数据分布之间的W 距离。由于相邻时刻的两种变换具有连续性，没有发生突变，那么相邻的两个分布之间的距离将趋于较小，具有时间一阶稳定性。增强的样本时间序列具有连续性，稳定提取特征的采样点输出值在时间一阶角度下计算得到的W 距离值序列也将趋于稳定，而部分采样点提取的噪声信息将不具有稳定性。

为了评估节点响应调制变化的能力，本文采用协整检验对序列数据在各节点的输出以及由调制曲线采样得到的参数序列数据进行检验。协整是考察两个或者多个变量之间的长期平稳关系，能够在具有单独随机性趋势的几个变量之间找到稳定的关系［35］。经过时间一阶平稳性验证后，通过协整检验可以发现模型中能够对调制序列作出响应的部分采样点。对于二元时间序列X、Y，如果存在非零线性组合β=（β1，β2），使得Z=β1X+β2Y弱平稳，则认为两个分量X和Y存在协整关系［36］。

对数据集中的每一个类别的增强样本数据单独进行考虑，保留能够稳定提取该类别特征信息的部分采样点，去除提取与该类别无关信息的部分采样点。考虑每个采样点对应的W 距离值序列的标准差序列，将标准差大于指定阈值的部分采样点看作无法稳定提取该类别图片的核心语义信息。根据一般神经网络剪枝的规则［37］，将这部分采样点的输出值置为0。保留W 距离序列标准差低于一定阈值的dimdenoise个采样点。最后，通过协整检验筛选掉不具备协整关系的部分节点，完成对预训练模型的修剪。文献［38］指出网络修剪本质上其实是最优网络结构的搜索过程，即以监督的方式，为每一类数据都构建了一个新的网络结构，能够保留模型提取的潜在有效信息。

3 基于资本资产定价模型的表征向量生成

传统的卷积结构以及池化结构都只考虑邻近像素或采样点之间的相关性，而忽略了与其他采样点之间的协作关系，从而导致大量有效信息的损失。并且在小样本数据的情况下，模型发现的相关性关系往往缺少泛化性［31］。相较于直接构建多分类模型，本文方法引入资本资产定价模型为数据集中的每一个类别构建单分类模型，基于最优传输理论，计算W 距离衡量采样点间的相关性，通过无需梯度传播的正向学习特征图中采样点之间的组合关系，生成能够使单类样本与其他类具有明显区分性的类别感知表征向量。

卷积结构中每个采样点所提取的特征偏重于不同的信息，如轮廓、纹理等［39-40］。将不同的采样点看作资本资产定价模型中的不同股票，采样点之间的组合看作资本市场，沿用CAPM 中的定义，将收益序列的标准差看作CAPM 中的市场风险。在已知收益序列的情况下，可以直接计算出组合内采样点的最佳权重，证明如下：

假设有N个风险资产，它们的收益率用随机变量r表示：

资产投资组合中它们的份额记为Q：

设eN×1=[1 1…1]T，则有eTQ=1，即所有投资份额的总和为1。则期望收益向量为：

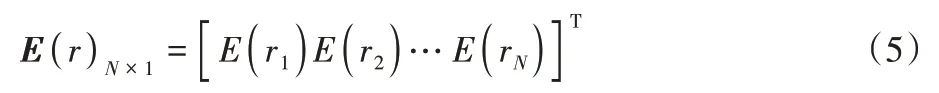
协方差为：

同时记协方差矩阵为V，对于某一投资组合p而言：

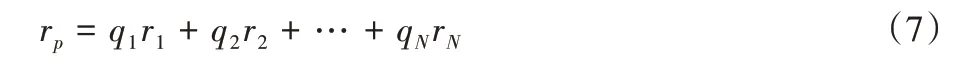
期望收益和收益方差分别为：

此时的优化目标为在给定收益期望μp的情况下，最小化风险即：

在此，假设V是正定矩阵，此时V的逆存在。构造拉格朗日辅助函数：

使目标函数取得极值：

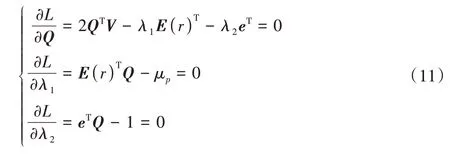
得：

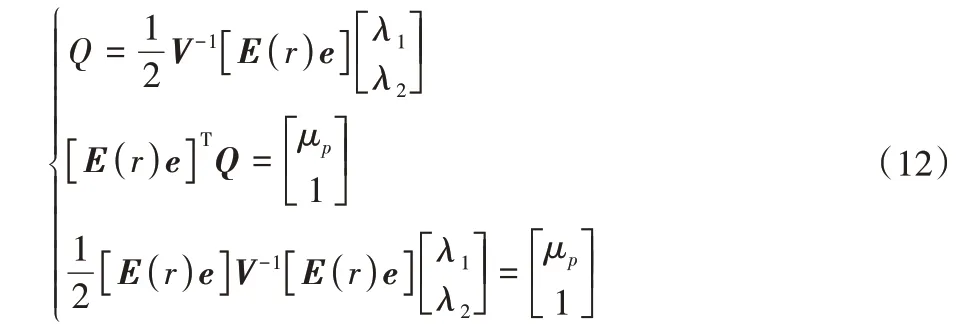
记[E(r)e]V-1[E(r)e]为A，则：

将式（13）代回式（12）得到权重向量最优解：

因此当收益和风险的定义方式确定后，可以计算其特征合成的权重最优解Q*，然后对组合内采样点值进行加权求和作为新采样点是输出结果，这一结构也可以看作是一种选择性连接［41］。

根据最优传输理论，可以通过计算不同采样点对应的数据分布之间传输的最小代价对不同采样点之间的协作关系进行评估，而W 距离能够近似两个分布之间的最优传输代价，因此本文首先基于W 距离计算采样点的相关系数矩阵来衡量采样点之间的相关程度，高相关系数代表采样点间存在增益关系，低相关系数代表采样点间存在互补关系，然后将增益互补的采样点组合在一起将能够将不同意义的信息结合在一起，对单个采样点提取的特征信息进行增益以及补充，提高采样点提取特征信息的能力。

首先对数据集中的不同类别的增强样本数据分别从空间角度进行考虑。对于卷积结构输出的特征图中的每一个采样点，从空间角度看，形成了一个空间样本序列，序列中的每一组数据可都看作一个数据分布。以其中一组为标准分布P0，将空间序列中每一组数据形成的分布Pi与之计算W距离，计算公式如下：

其中：Wij代表第i（1≤i≤dimdenoise）个采样点对应的空间序列中第j（1≤j≤n）组分布与标准分布之间的W 距离。由于每一组数据都是由同一类别样本中的一个样本经过变换得到的增强数据，所以可看作是该类别图片的类内距离Win，得到类内W 距离矩阵。基于类内W 距离矩阵计算得到相关系数矩阵C，用于衡量采样点间的协作关系。

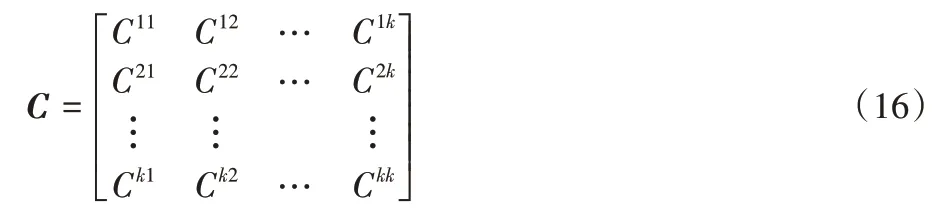
其中：Cij表示第i个采样点与第j个采样点W 距离序列之间的相关系数。类似地，再从数据集中随机选择其他类增强图片空间序列作为类外图片，保证类外多样性，将序列中每一组数据形成的分布与同类内图片的标准分布计算W 距离，作为该类别图片的类外距离Wout，得到多组距离后取均值与类内距离序列保持统一维度，因此可定义采样点的收益函数R：

通过计算可得到收益矩阵，为了添加类内的多样性，本文从空间序列数据中重新选择不同的数据分布作为标准分布，并对分布取平均，重新计算得到包含类内多样性的收益矩阵，并且数据分布也将更加稳定。

由于所有采样点的感受野都已经覆盖了整个样本图片，相较于根据相关系数从所有采样点中选择采样点进行组合，本文方法选择所有采样点中收益最大的一部分采样点作为备选采样点，再依据相关系数矩阵从中选择采样点进行组合，以最大化特征信息质量。以特征图中的每个采样点作为中心采样点，从备选采样点中选择采样点进行组合，即资本市场，再根据组合内采样点的收益序列矩阵计算夏普比率得到各个采样点的最佳的权重，加权求和之后生成单分类特征向量，其收益提升，并且分布更加稳定，得到了更高质量的特征表示。

本文方法的整体框架如图3 所示，针对图片多分类（K类数据）任务，首先获取增强样本图片序列经过预训练模型卷积层输出得到的原始特征向量，基于分布稳定性检验以及协整检验生成K种噪声定向修剪方式，原始特征特征向量分别经过K种噪声修剪方式得到K个经过修剪的向量。然后基于资本资产定价模型生成K种节点组合方式CAPMi（1≤i≤K），对修剪后向量中的节点进行重新组合生成类别感知表征向量。即从数据分布的角度为数据集中的每一个类别都构建了全新的结构，通过无需梯度的正向学习更好地提取指定类别相关的信息，解决了传统卷积结构以及池化带来的信息损失的问题，同时也避免了基于梯度下降进行优化带来的问题。

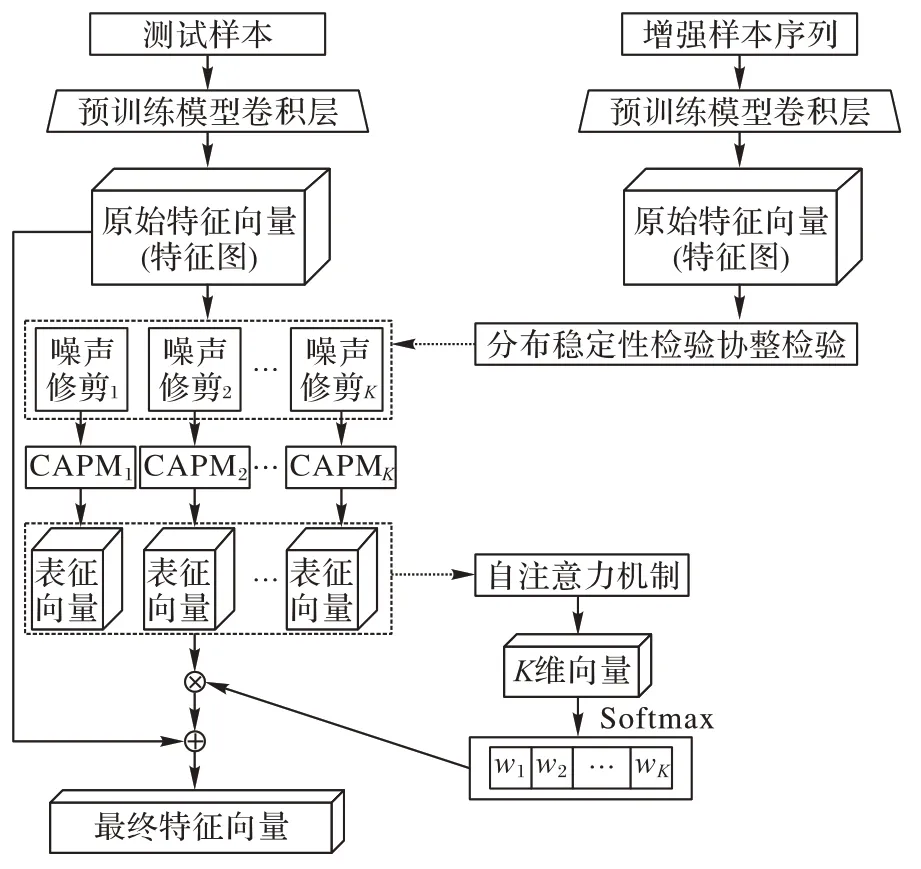
图3 本文方法的整体框架Fig.3 Overall framework of the proposed method

4 基于自注意力机制的多分类模型

经过资本资产定价模型组合后生成的表征向量完成了特征稳定提取的过程，这些表征向量分别包含不同类别信息，并且它们之间具备稳定的偏序关系；但这一结果无法作为特征向量用于特征分类，构建多分类模型还需要将这些特性信息融合在一起生成统一的特征向量。如果将这些表征向量简单地连接起来，类别之间的互信息将会丢失，难以得到最优的结果，因此需要制定方法学习表征向量之间的互信息并进行融合。

文献［42］中在人脸识别任务上提出了一种基于自注意力机制生成权重的方法。自注意力机制是一种注意力机制改进方法，不借助外部信息，而更专注于数据内部之间的关联性［43］。人脸样本经过不同的组网络生成包含胡子、肤色等不同属性的组感知向量后，基于卷积层输出的特征图，生成多个组感知表征向量的权重，再将所有的组感知表征向量加权生成最终的特征向量，其模型性能优于传统的人脸识别模型。

因此可以考虑根据样本图片归属于某一类别的概率对这些信息进行融合，概率最大的类别感知表征向量贡献也将越大。类似地，本文方法引入自注意力机制实现表征向量之间互信息的融合。由资本资产定价模型所生成的多个表征向量可看作一个整体，通过计算自注意力能够挖掘不同表征向量之间的互信息，并且可以得到单类别表征向量与整体语义空间的关系，从而指导权重向量的生成，完成对多个表征向量的融合，为最终生成统一的特征向量提供有效的信息。

基于自注意力机制，本文方法采用scaled dot-production attention［43］进行相似度计算得到的注意力，自适应地生成类别感知表征向量的权重，其结构如图4 所示。针对K个类别的数据，以监督的方式生成K维的向量，使用Softmax 方法对其进行归一化处理，将其作为K个类别感知表征向量的权重向量，与类别感知表征向量做加权求和处理，完成对信息的融合，增强了数据之间关联性。由资本资产定价模型（CAPM）组合生成的表征向量偏重于样本与各个类别的关联信息，但也存在部分信息的损失，因此，将其与去噪后的特征图相加，两者形成一种信息的互补，最大化有效信息，生成最终特征向量，结构如图4 所示。通过全连接层对特征向量进行聚合，可以生成具有弱相关性的embedding 向量。

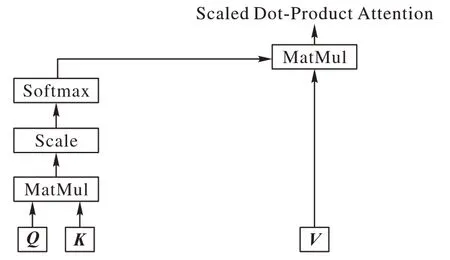
图4 自注意力机制结构Fig.4 Structure of self-attention mechanism

5 实验与结果分析

5.1 实验设置

5.1.1 数据集

对于训练，本研究采用ImageNet 2012 数据集［44］中的训练集，其中包含1 000 类图片，每类1 300 张图片，从中随机选择K=10 和K=100 类图片，每类随机选择25 张图片构建小样本量级训练集。对于测试，采用ImageNet 2012 数据集中的验证集，其中包含1 000 类图片，每类包含50 张图片。另外本研究在CIFAR-100 数据集［45］重新进行了同样的实验，其中包含100 类图片，每类各有500 个训练图片和100 个测试图片，并且每个图片都带有类别标签以及超类标签，可用于评估概念层次间的偏序关系。训练过程中，每类随机选择了25 张训练集图片构建小样本量级训练集，其他数据构成测试集，并在该测试集上进行测试。

5.1.2 度量指标

在本文方法中，统一采用W 距离对数据分布之间的距离进行评估。在网络修剪实验中，考虑到样本不平衡的情况，采用召回率在ImageNet 2012 验证集上进行评估。在最终模型性能评估实验中，采用Top1-Acc 和Top5-Acc 分别在ImageNet 2012 验证集和CIFAR-100 测试集上进行评估。

5.1.3 实验设置

实验是基于Pytorch 深度学习框架下完成的，硬件配置如下：处理器为Intel Xeon gold 6320，内存为32 GB，GPU 为NVIDIA GeForce RTX 2070。对于输入的图片，分辨率大小统一调整为224×224×3，并使用均值向量（0.485，0.456，0.406）以及标准差向量（0.229，0.224，0.225）对图片进行标准化处理。

5.2 网络剪枝性能评估

在数据增强过程中，本文方法采用了高斯模糊、尺度变化、滑动窗口等方式对样本作了连续性增强，生成了序列数据。考虑K类增强的数据样本，每个类别都计算得到一个长度为dimorigin的标准差向量Si（0≤i≤K）。需要定义噪声筛选的阈值，筛选出大于此阈值的采样点编号集合，对应于特征图中的采样点编号，将对应的值将置为0，即构建得到K种网络结构修剪方法。从图5 可以观察到，部分噪声采样点的标准差异常大，可看作无法对同类别图片稳定提取信息。为了避免标准差向量中极值的影响，本文选择标准差向量中小于中间值的部分数据定位为Smid，阈值τ表达式定义为：

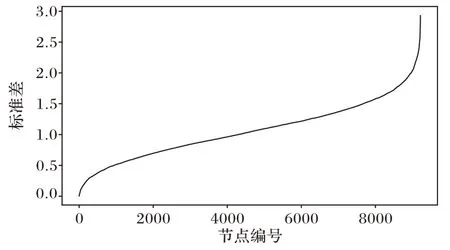
图5 随机类别对应的排序后的标准差分布Fig.5 Sorted standard deviation distribution corresponding to random class

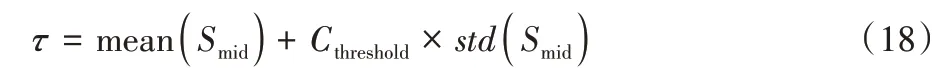
其中：Cthreshold为常数，在实验中根据统计学相关经验以及多次实验将其取值为5 能够筛选掉20%左右的噪声采样点。随后通过协整检验保留置信度大于95%的部分采样点完成对网络模型的修剪。

为验证经过修剪后的网络结构性能，构建K个与AlexNet 预训练模型中的全连接层同样结构的二分类器进行验证，对于K类中的每一个类别，选择该类的20 张图片作为正类，另外从ImageNet 2012 数据集中随机选择20 类，每个类别选择20 张图片，共400 张图片作为负类，获取经过按照本类修剪方式修剪后的特征图，输入到模型中完成训练，获取测试集样本输出的指示向量，以召回率为指标评估K个二分类模型性能。观察图6 可以看到当K=10 时，预训练模型经过修剪后，其中8 个类别的召回率得到了提升，说明通过检验时间一阶数据分布的稳定性确实能够剔除与类别核心语义信息无关的噪声，提高模型稳定提取特征信息的性能。

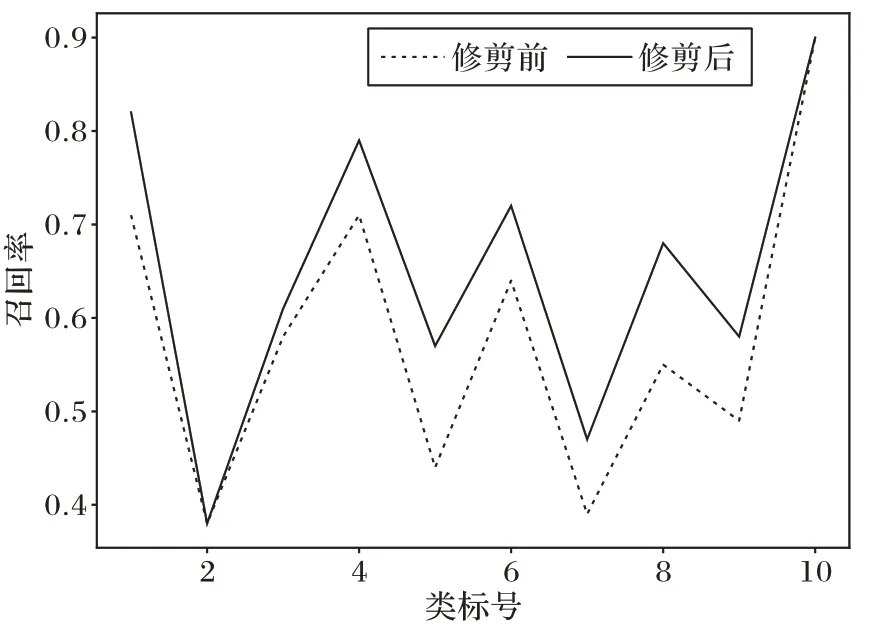
图6 模型经过修剪后，单类别召回率普遍提升Fig.6 Most single class recall rates increasing after model pruning

另外，本文方法探究了不同类别对应的修剪后网络模型有效结构的相似程度。选择蛇、蝴蝶、猫、猎豹、狗、鱼、鸟、蜘蛛几个纲目作为实现对象，从ImageNet 2012 训练集中属于这些纲目的部分类别中随机选择小样本量级的样本作为实验数据。按照第3 章所阐述的方法，针对这些类别对模型进行修剪分别生成各自对应的有效结构，计算每个类别保留的采样点编号，模型相似比例为修剪后模型保留采样点的编号的交集大小，以物种猫为中心的结果如图7 所示，其中sna、but、cat、le、dog、fish、bird、spi 分别代表蛇、蝴蝶、猫、猎豹、狗、鱼、鸟、蜘蛛。观察猫与其他物种的单分类模型相似比例，可以看到猫与同物种的其他猫类相似比例最高，除此外，与狗和猎豹两个物种的相似比例较高，这也符合人类对于物种的视觉认知，这一结果表明模型中不同类别之间存在稳定偏序关系的可能性，CNN 模型本身具备提取概念层次特征信息的能力，也说明本文方法能够使模型在最优路径上进行传输。

图7 不同物种对应的单分类模型有效结构相似比例Fig.7 Similar ratios of effective structures of single classification models for different species

5.3 模型性能评估

经过修剪后的特征图中采样点已经能够稳定提取信息，而这些采样点之间的相关性仍然比较大，为了节约计算成本，考虑最大化收益以及信息的多样性，对于每个采样点，根据相关系数矩阵另外选择相关系数最大的5 个采样点以及相关系数最小的5 个采样点，一共11 个采样点作为CAPM 中的资本市场。每个采样点可计算得到收益序列以及标准差，可计算最优市场组合，即11 个采样点的最佳权重，加权求和之后作为新生成的表征向量中的一个采样点。得到新的表征向量后，采用第4 章中阐述的方式计算每一个采样点的收益，观察经过选择性组合前后采样点的收益变化来评估类别感知表征向量的性能。

随机选择类别观察部分节点经过CAPM 组合优化前后的收益变化，结果如图8 所示，可以观察到通过本文方法所构建的新结构对节点进行重新组合后，新生成的表征向量中采样点整体的收益都得到了提高，即单类别的区分性得到了显著提高。另外，实验中随机选择了部分采样点观察它们经过资本资产定价模型组合前后在分布上的变化，图9 为3 个节点组合前后的W 距离分布情况，即类内距离Win和类间距离Wout。可以观察到经过组合后，Win分布更加平稳，并且能够与Wout分布明显区分开来，这一结果表明本文方法能够显著提高不同类别样本之间的区分性。

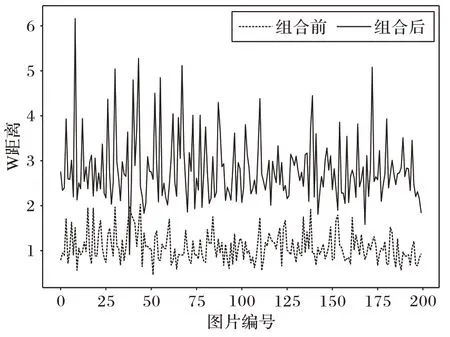
图8 随机选择类别，资本资产定价模型组合优化前后所有采样的收益R分布Fig.8 After randomly selecting a class，distribution of income R of all samples before and after combinational optimization of capital asset pricing model

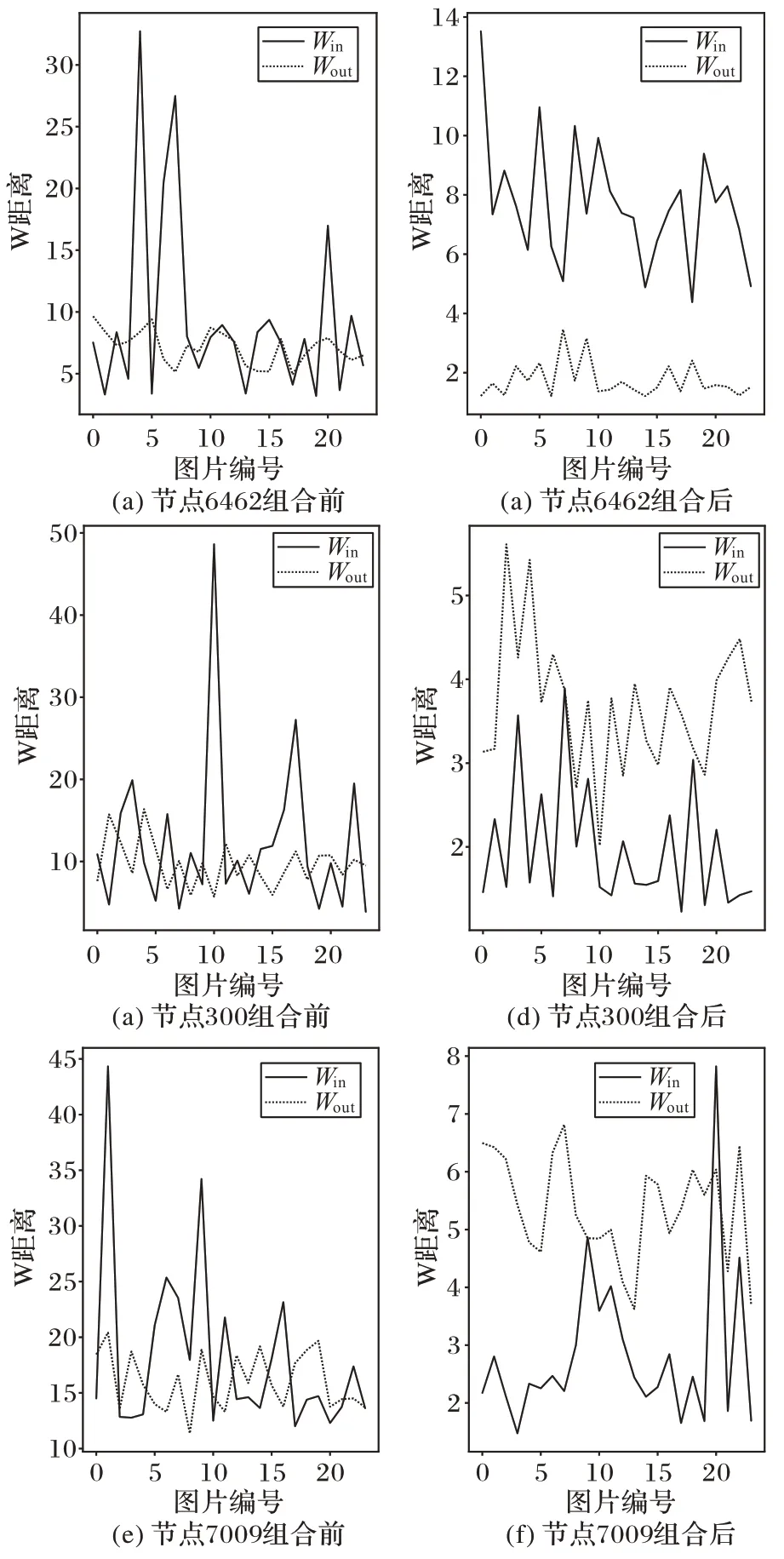
图9 资本资产定价模型组合优化前后单采样点的可区分性Fig.9 Distinguishability of single node before and after combinational optimization of capital asset pricing model

为了评估本文方法生成的最终特征向量性能，构建一个包含3 层全连接层的多分类模型并计算准确率Acc 作为评价指标。首先评估原始网络结构的性能，获取训练集样本输入预训练模型的原始特征向量进行训练，将测试集样本输入多分类模型得到输出指示向量，计算准确率作为预训练模型的基准性能。然后将训练集样本对应的原始特征向量输入到本文方法所构建的网络结构中，得到新的特征向量，输入到同样结构的全连接层完成模型训练，获取测试集样本对应的指示向量，仍计算准确率作为提出的方法性能。

分别在ImageNet 2012 数据集上随机选择100 类以及CIFAR-100 数据集上进行评估，结果如表1 所示，模型经过改进后，在ImageNet 2012 数据集100 类图片上Top-1 Acc 从58.82%提高到了68.50%，Top-5 Acc 从83.51%提高到了92.25%。在CIFAR-100 数据集上Top-1 Acc 从61.29%提高到了69.15%，Top-5 Acc 从81.43%提高到了89.55%。这一结果表明本文方法能够基于小样本量级的训练数据显著提升CNN 预训练模型的性能。

为验证本文算法能够直接应用到其他卷积神经网络模型中，使用同样的方法分别对ResNet 预训练模型进行修改对性能进行评估，结果显示在表1 中，Top-1 Acc 和Top-5 Acc分别由78.51%和94.20%提高了85.72%和96.65%，说明本文方法能够直接应用到主流的卷积神经网络预训练模型中，不需要做复杂定制化处理。

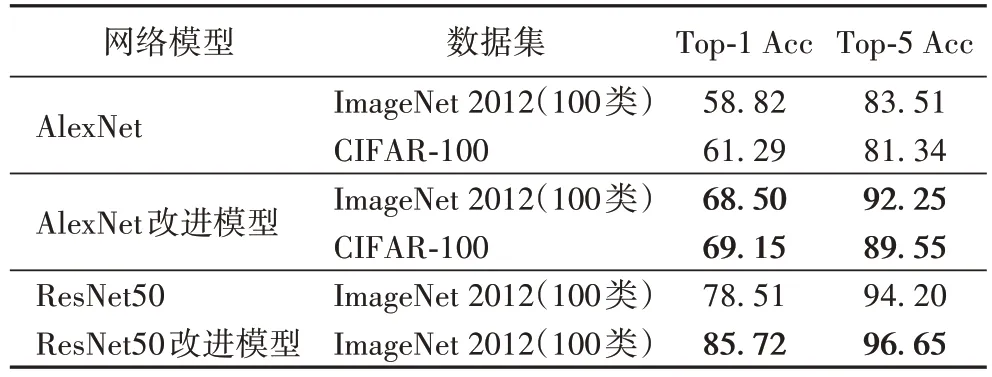
表1 图片分类任务性能比较 单位：%Tab.1 Performance comparison of image classification tasks unit：%

6 结语

本文提出了一种基于资本资产定价模型以及小样本的无需梯度传播的正向学习的方法，为小样本生成序列化增强样本数据，并通过协整检验分析因果关系对预训练模型的结构进行修剪并选择性构建一种新的结构，能够更好地提取特征信息，并通过无需梯度传播的正向学习生成了质量更高的特征向量，解决了传统神经网络优化过程对梯度的依赖；并且进行了一系列实验对网络结构以及特征向量质量进行了评估，表明本文方法能够明显提高预训练模型的性能和泛化能力，并且能够直接应用到主流的卷积神经网络模型中，无需做定制化处理。未来计划寻找更多的有效策略对模型中的采样信息进行整合和提炼，利用协整分析和CAPM 等干预方式来降低模型的复杂度并进一步提高模型性能。