高电压增益阻抗源逆变器的小信号模型分析

程谆

湖南铁道职业技术学院，湖南 株洲 412001

0 引言

新能源发电技术已成为抑制环境污染和能源危机的有效途径[1-4]。并网逆变器作为新能源发电并网的核心部件近年来发展迅猛[5-8]。

2002年彭方正教授提出了一种Z源逆变器拓扑结构，解决了传统逆变器中的诸多问题，为国内外学者提供了一种全新的思路[9]。近年来，为了进一步提高阻抗源逆变器的升压能力，降低其开关应力，国内学者不断探索，对阻抗源逆变器拓扑结构进行了研究，主要通过在阻抗源网络中引入变压器、耦合电感、开关电感来提升这方面的性能[10-16]。文献[10]提出的改进型Z源逆变器，将三相逆变桥与阻抗源网络位置颠倒，在一定程度上抑制了启动时存在的电流过冲，它与Z源逆变器相比，在相同的直流链电压下其电容电压应力更小，但升压能力不足。文献[11]提出的准Z源逆变器，在相同的升压比下其电容电压应力降低，并且通过合理调节电感L1的位置，使得输入电流连续，但其升压能力仍然受到调制因子的制约。文献[12-13]提出的T型Z源逆变器，引入了漏感很小的变压器代替Z源逆变器中的两个电感，并减少一个电容，进而通过改变变压器变比和直通占空比来灵活调节输出电压。相较于Z源逆变器，在相同的直通占空比和调制因数下，T型Z源逆变器可以通过调节变压器变比提高输出电压从而提高其升压能力，并且减少了无源器件的个数，使得逆变器尺寸减小、成本损耗降低。但是随着变压器变比的增大其漏感也会增大，反而会导致变压器直流侧链电压降低，从而使得升压效果受到抑制。文献[14]提出的开关耦合电感Z源逆变器，用含有耦合电感的无源网络替代其中一个电感。当耦合系数k接近于1时，可调节耦合电感的匝比和直通占空比来获得更大的电压增益。但是耦合电感会带来漏感，在非导通模式下，会产生电压尖峰缩短桥臂上器件的使用寿命；而且，虽然其升压能力会随着匝数比的增大而增大，但是过大的匝数比会导致变压器体积增大使得铜损增加效率降低。文献[15]提出的开关电感Z源逆变器，相较于Z源逆变器，虽说多了6个二极管和2个电感使得成本增加，但是只需要极短的直通状态即可获得较高的升压比，从而避免了升压比和调制因数的矛盾关系，使得升压能力得到了显著提升。但由于电容电压初始值为零，开启时会产生很大的浪涌电流；并且其仍然存在Z源逆变器输入电流不连续等问题。文献[16]提出的一种开关电感准Z源逆变器，将准Z源逆变器中的一个电感替换为一个开关电感支路，使得其具备开关电感Z源逆变器升压能力强的优势，并且保留了准Z源逆变器输入电流连续的优点。文献[17]提出的一种高电压增益阻抗源逆变器，它较传统Z源逆变器具有更高的电压增益和更低的电流谐波。

本文针对高电压增益阻抗源逆变器进行研究。首先从直通和非直通状态入手，分析其稳态工作原理；然后推出升压因子和直通占空比的表达式。并且运用状态空间平均法建立状态空间方程，引入小扰动建立其小信号方程，通过对波特图和零极点轨迹的分析得出阻抗源网络电容电感值大小对于系统稳态性能和动态性能的影响，可为系统参数设计提供理论指导。

1 拓扑结构及稳态工作原理

高电压增益阻抗源逆变器的拓扑结构如图1所示，分别讨论直通情况与非直通情况，并进行分析。

图1 高电压增益阻抗源逆变器拓扑结构

当网络处于非直通状态时，二极管导通情况如图2所示。

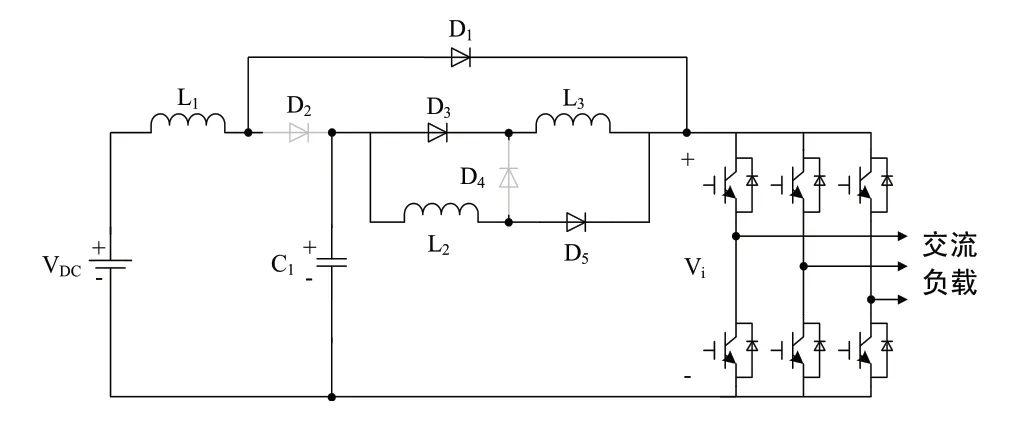
图2 直通时系统的等效电路

可得如下式（1），并且其中Vi=0：

当网络处于非直通状态时，二极管导通情况与直通时相反，如图3所示。

图3 非直通时系统的等效电路

可知：

式（2）和式（3）中：VL1、VL2、VL3分别表示电感L1、L2、L3两端的电压；VC1表示电容C1的电压；iC1表示电容C1的电流；iL1、iL2、iL3分别表示电感L1、L2、L3两端的电流；VDC表示直流电源电压；Vi表示高电压增益阻抗源网络的输出直流电压。

在一个开关周期T中，直通时间为T0，非直通时间为T1，直通占空比为d0=T0/T。高电压增益阻抗源逆变器网络电感L1的端电压平均值VL1、高电压增益阻抗源逆变器网络电感L2的端电压平均值VL2、高电压增益阻抗源逆变器网络电感L3的端电压平均值VL3均为0，可知：

上式中：VL3NST、VL2NST分别表示非直通状态时电感L1、L2两端的电压。

由式（3）可得：

可知，高电压增益阻抗源网络输出电压的平均值Viav可表示为：

2 小信号模型分析

假设系统工作在电流不断续的状态，并假设L1=L2=L3=L0定义四个状态变量为：

那么将直通状态下高电压增益阻抗源逆变器的等效方程（1）转化为的形式，可得：

其中：

同理，此式中矩阵系数对应的分别为：

由[（5）*d0+（6）*（1-d0）]，可以得到系统状态方程：

使用状态空间平均法对高电压增益阻抗源逆变器进行建模，获得大信号方程为：

使用状态空间平均法，得到矩阵A为：

矩阵B为：

此处的d0为系统动态时的直通占空比。

同样，利用状态空间平均法，可得系统网络的静态工作点为：

其中：

上式中，D0为系统网络稳态工作点的直通占空比。同理：

其中，IL1、IL2、IL3、VC1分别为静态工作点的电感电流及电容电压。

是静态工作点的输出电压。

由式（9）可知，系统状态为稳态时：

对平均模型中的状态变量进行小信号扰动，建立小信号模型。将扰动小信号，依次带入式（8）中，可得：

将其再代回（9）式，即可化简为：

对上式进行拉式变化可得：

由上式可知系统输入的扰动量就是：输入的直流电压扰动（也就是输入电压扰动），以及直通占空比的扰动。因此，只需将其中一个小信号扰动量设置为零，就可以得到另一个输入状态变量的小信号传递函数。

可知，直通占空比控制至电感电流iL1的传递函数为：

在上式中：

直通占空比控制至电容电压vC1的传递函数是：

输入电压（直流侧）至电容C1的传递函数为：

3 动态性能分析

通过式（24）和式（25），采用表1所示的系统参数，绘制出小信号传递函数GVd1（s）和Gid1（s）的零极点轨迹如下。

表1 高电压增益阻抗源逆变器仿真参数

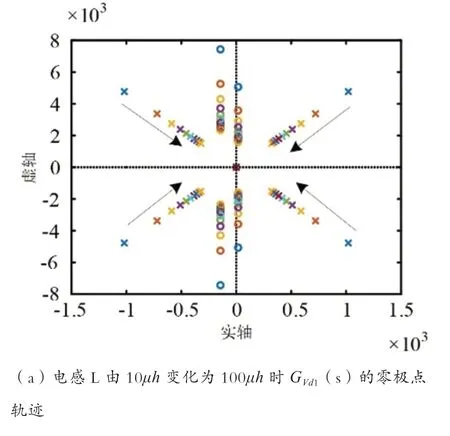
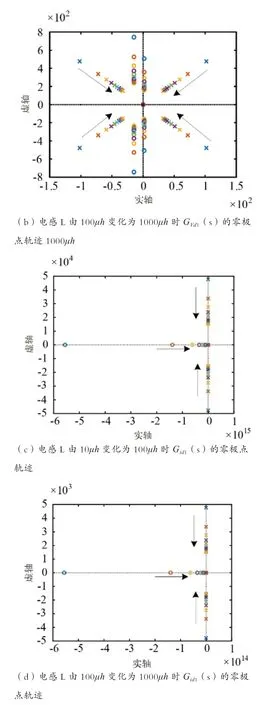
图4 电感变化时的零极点轨迹

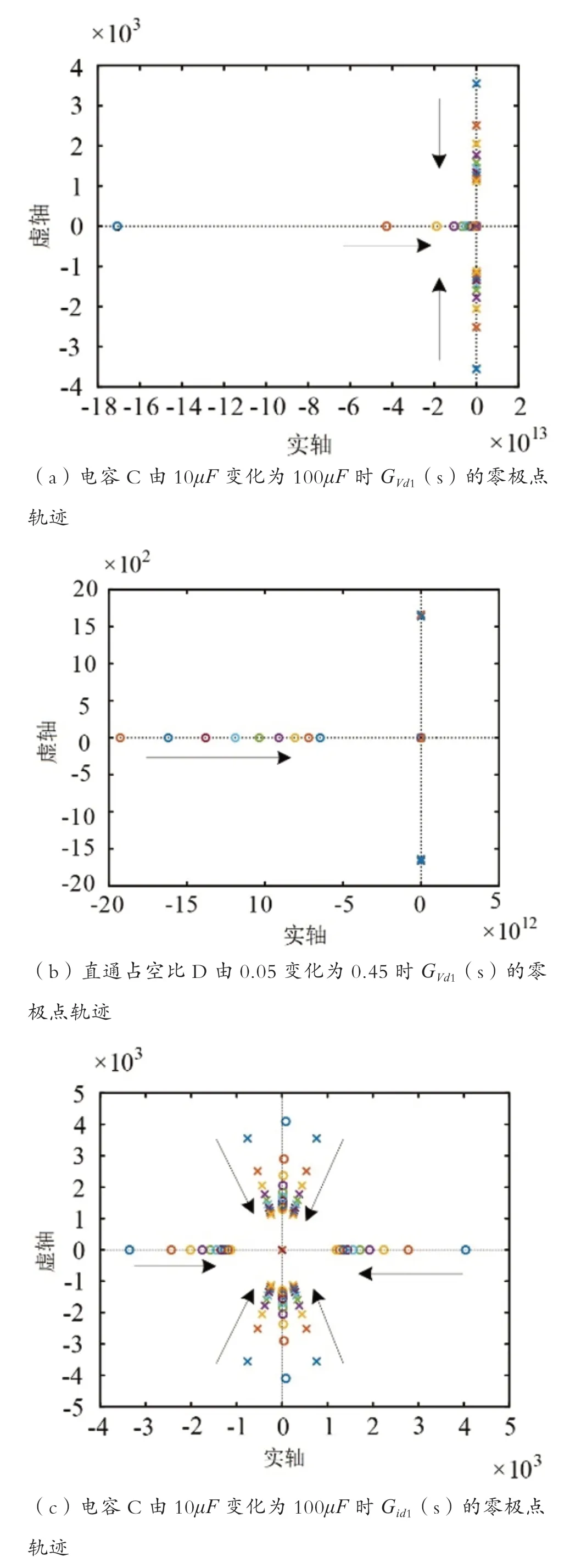
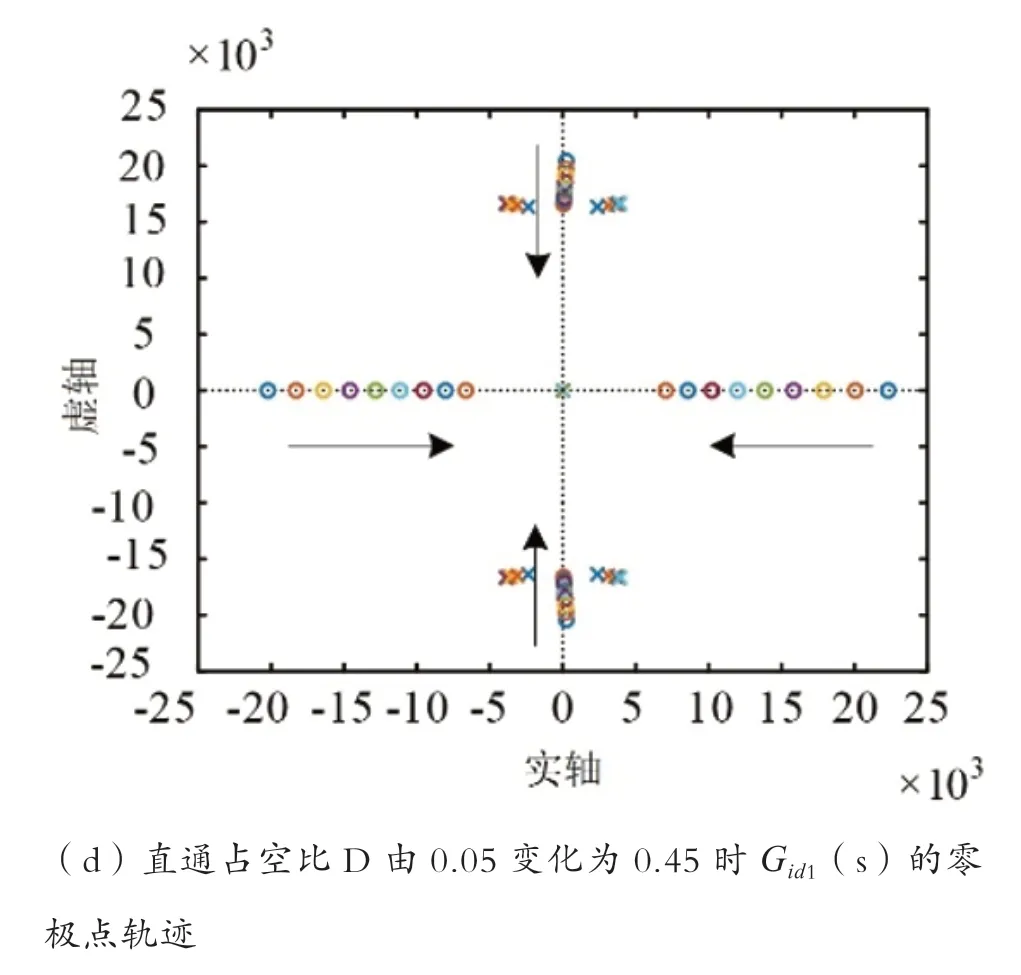
图5 电容或直通占空比变化时的零极点轨迹

由图分析可知，位于虚轴右侧的零点不会因电容参数的变化而发生变化，但是当系统中电感值或者直通占空比增大时，右侧的零点会移向虚轴。

4 结语

本文针对高电压增益阻抗源逆变器，建立了其小信号模型，在此基础上，得到了各个状态变量的小信号传递函数，并依据小信号传递函数得到系统零极点模型。分析了高电压增益阻抗源逆变器的动态性能与阻抗源网络电感、电容参数以及直通占空比之间的关系。得出阻抗源网络电感、电容值越大，系统动态响应越慢，因此在进行参数设计时要兼顾稳态、动态性能，电感、电容取值不应过大。