基于线性相关模型的车温报警算法

李志鹏

江西财经大学，江西 南昌 330013

0 引言

随着经济的快速发展，很多家庭将汽车列为“必需品”，周末家人可驾驶汽车到附近的旅游点放松心情。汽车方便着大家的出行，但安全问题越来越受到大家的关注。2015年5月27日，广西一辆汽车内，一位12岁的孩子被发现时已经死亡，同日，湖南湘潭，一位4岁的男孩被遗留在自驾车里，发现时已经窒息；2021年9月20日，一位幼儿园儿童被困在车内9个小时，被发现时已经死亡；2022年4月23日，悲剧再次发生，一位3岁女童在车内闷死。孩子的行动能力和自救能力没有发育完全，在车内不能及时自救，最终导致悲剧的发生，如此多的悲剧，一次次重演，不得不让人深思，但对于快速发展的社会，很多人压力大，生活节奏快，家长一时大意，直接关车走人，当发现时后悔莫及。基于上述问题，本人提出了一种基于线性相关模型的车温检测报警算法，能够检测车温，当车内温度上升过快，或者温度过高时，自动打开车窗，及时报警，提醒车主及行人，防止悲剧的发生。

线性相关模型在多个领域发挥着重要的作用，如在大数据时代，以多样化的特征分析数据[1]，可以较准确地对统计数据做出推断和预测[2]；在税收或环境方面应用线性相关模型，预测生态与污染的相关性[3]；在网络共享领域，通过线性规划理论，提高对未知节点的预测能力[4]；还可以通过此模型恢复丢失的像素[5]。本文在线性相关模型的基础上设计车温报警算法，增加车内生物体的安全系数，减少悲剧的发生。

1 线性相关理论

设散点数据为(x1,y1)，(x2,y2)…(xn,yn)，令为x1,x2,x3…xn的平均值，为y1,y2,y3…yn的平均值，为了更好地观测数据是否成线性相关，将横纵坐标的数据均减去相应的平均值，形成新的坐标：

设：

则相关参数r为[6-7]：

当r＞10时，正相关，即一个变量变大时，另一个变量也相应增大；当r＜0时，负相关，即当一个变量变大时，另一个变量相应减小，r的绝对值越接近于1，两个变量之间的关系越相关，越接近于0，相关性越小。

根据r的大小可以判断两者的相关系数程度，但是不能具体描述成对数据形成的线性回归方程，求方程需要通过公式（2），计算出相应的斜率参数和截距参数：

则回归方程为：

2 算法设计

（1）首先判断车是否在行驶中，若是，说明有车主操控，车温检测报警算法不做任何操作；若否，则进行第二步操作。

（2）车内红外检测装置传感器检测车内是否有生物体指标（孩子或者宠物等），若否，车温检测算法不做任何操作；若是，则进行第三步操作。

（3）红外检测到有生物体在车内，车门车窗已关闭，启动车外、车内温度检测装置，收集数据，并将得到的数据分组处理，每过1s收集一次温度数据，十个数据作为一组，常温下是20℃左右，本文将20.0℃、20.5℃、21.0℃、21.5℃、22.0℃、22.5℃、23.0℃、23.5℃、24.0℃、24.5℃，作为车内、车外散点数据的横坐标，车内、车外检测温度均作为纵坐标。若车内检测温度超过37℃，直接启动开窗操作，并使用警报提醒车主。

（4）车外的坐标为（20.0，y外0），（20.5，y外1），（21.0，y外2），（21.5，y外3），（22.0，y外4），（22.5，y外5），（23.0，y外6），（23.5，y外7），（24.0，y外8），（24.5，y外6）。车内的坐标为（20.0，y内0），（20.5，y内1）（21.0，y内2），（21.5，y内3），（22.0，y内4），（22.5，y内5），（23.0，y内6），（23.5，y内7），（24.0，y内8），（24.5，y内9），。成对的坐标数据出来后，则按照公式（1）求相关参数r，设车外相关系数为r外，车内相关系数为r内。r差计算公式为：

其中：r差是两者绝对值差的绝对值。

（5）车温检测器每过1s传输一次温度数据，十个数据成一组，1min形成6组数据，对6组数据分别求r外，r内，并计算r差值，统计六次数据，预警参数h为：

其中：r差i是第i个r差。上限参数d公式：

其中：r外i为第i个车外相关系数，r内i为第i个车内相关系数。通过公式（2）计算车内数据对应坐标数据的斜率参数，则斜率参数平均值公式：

其中：yi为第i个车内温度检测值。

（6）判断h和d的大小，如果h＞d，预警参数超过上限参数，进行判断正负相关性，若，负相关，表示温度过低；不启动开窗操作，回到第（3）步，若，正相关，表示温度过高，若大于30℃，则开窗报警处理，提醒车主；若不大于30℃，则回到第（3）步；如果h＜d，回到第（3）步。

通过上述的6个步骤，即可计算出车外、车内温度的变化，并做出相应的处理操作。整个数据处理流程图如图1所示。

图1 数据处理流程图

3 算法结果

以南方某城市8月份中午12点，汽车在日照充足的情况下为例，车门关闭并上锁，红外检测装置检测到车内有生物体指标时，启动报警检测装置。1min内检测到车外温度为：32.1，32.2，32.4，32.3，32.5，32.7，32.8，32.9，33.0，33.1，33.2，33.4，33.3，33.5，33.4，33.3，33.6，33.4，33.5，33.7，33.8，33.9，33.7，33.8，33.6，33.4，33.5，33.6，33.7，33.6，33.8，33.9，34.0，33.8，33.9，33.7，33.6，33.7，33.8，33.9，33.8，33.7，33.6，33.7，33.6，33.7，33.8，33.7，33.8，33.6，33.7，33.8，33.9，34.0，33.8，33.9，33.7，33.6，33.8，33.9。车内检测到的温度为：24.1，24.2，24.3，24.5.24.7，24.8，24.9，25.1，25.3，25.5，25.6，25.7，25.9，26.2，26.4，26.5，26.8，27.0，27.2，27.4，27.6，28.0，28.3，28.5，28.6，28.9，29.2，29.5，29.7，30.1，30.5，30.9，31，3，31.7，32.0，32.3，32.5，32.6，32.8，33.0，33.2，33.4，33.5,33.8,33.9,34.1,34.4,34.2,34.6,34.8,35.0,35.1,35.3,35.4,35.6,35.8,35.9,36.2,36.7,36.8。形成六组车外坐标、相关系数r外及回归方程斜率参数（表1）。

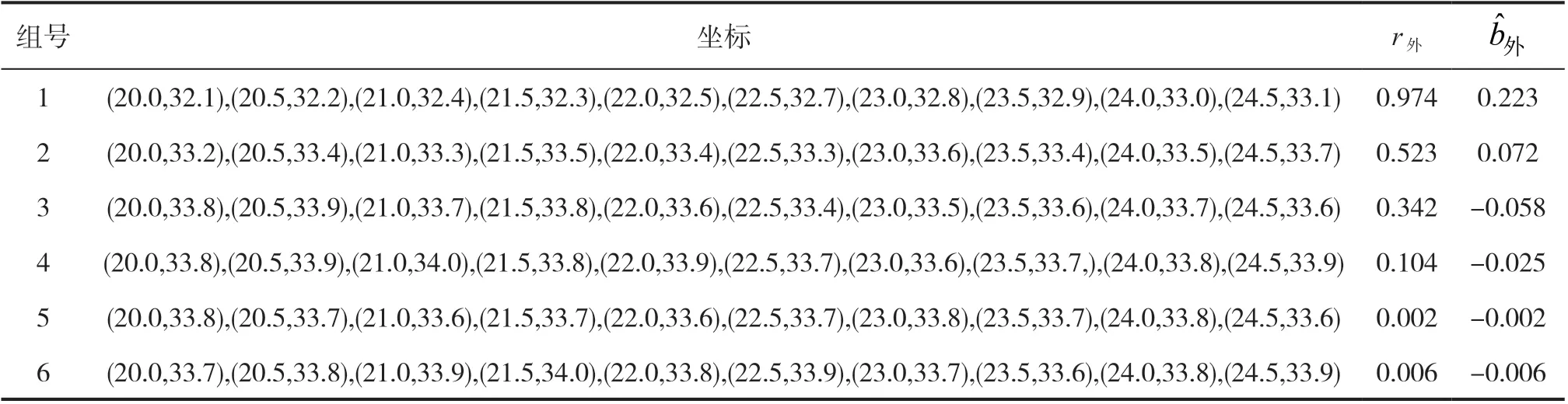
表1 车外温度坐标、相关系数及斜率参数

形成六组车内坐标、相关系数r内及回归方程斜率参数（表2）。

表2 车内温度坐标、相关系数及斜率参数

形成r外，r内，r差，h，d（是车内各组斜率参数的平均值），（表3）。

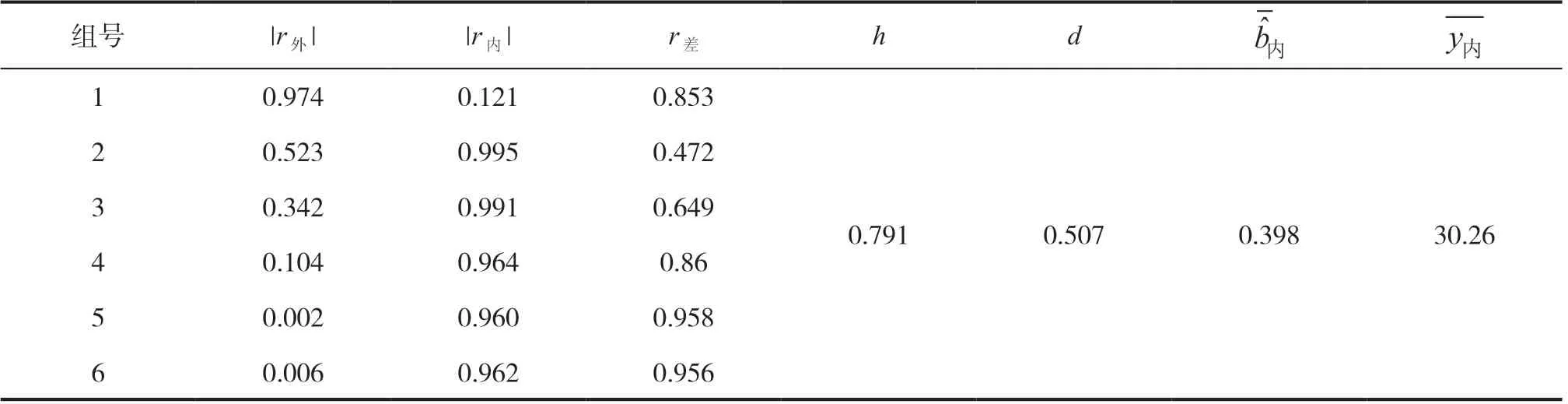
表3 r外，r内，r差，h，d，

通过表格不难发现，在1min内，参数h＞d，报警装置启动，提醒车主，同时大于零，正相关，表示温度升高，是30.26℃，大于30℃，开窗处理。开窗后可防止车内温度过快升高。

4 算法讨论

此算法主要是针对汽车内升温或降温过快设计的，通过车外和车内温度的对比，当车外温度变化不大，车内温度变化过大时，此算法的优越性凸显，可以在短时间内发现危险情况，若h＞d，且温度上升时，打开车窗，报警提示，提醒车主；若h＞d，且温度下降时，提醒车主，但不能打开车窗。此算法的优点为快速发现车内温度变化情况，并及时做出响应。但此算法的缺点为当车外温度变化过大，车内温度变化不大时，按此算法也得出h＞d，给出的指令也是开窗，因此算法还可以继续优化。但车外温度短时间内变化大的情况较少，此算法可以较好地处理通常情况下车内温度升高过快的情况。

5 结语

通过线性相关理论，设计的算法可以检测到车外、车内温度的变化，升温过快或车内温度超过37℃，落下车窗并及时报警，防止生物体因温度过高惊恐、窒息、死亡等，有效防止悲剧的发生。