培养初中学生数学讲题能力的策略
文/ 阳山县教师发展中心 欧阳红峰
数学学习的过程是思维活动的过程,而交流是促进思维活动的重要环节,《义务教育数学课程标准(2011 年版)》也明确指出:动手实践、自主探索与交流合作是学生学习数学的重要形式。对于一道数学题,学生听懂了不一定会做,会做不一定会说,因此“讲题”是最高层次的学习方式。在初中数学教学中开展数学讲题活动,让学生在讲题的过程中学会表达,在与同学的交流中展示自己的思维过程,能有效提高他们的数学表达交流素养。为此,我们进行了“山区初中学生数学自主学习习惯培养的实践研究”(广东省教育科研“十三五”2018 年规划课题),旨在通过研究,提升学生的“表达交流”和“自主反思”素养,从而形成良好的数学学习习惯。以下是课题组在利用“讲题”培养学生数学表达交流素养方面的几个策略:
一、构建和谐课堂,让学生“敢于”讲题
案例1:“平行四边形的性质2”教学片断
清远市第26 届中小学青年教师基本功比赛初中数学总决赛有一个比赛项目是课堂教学展示,展示的课题是北师大版八年级下册第六章的“平行四边形的性质”第2 课时,阳山县参赛选手李老师在该课的教学中,对教材中138 页例题2的处理方式是让学生先自主阅读,然后到讲台上讲解。
经过集体的备课研讨,我们对这个环节的教学预设了以下情形:情形一,学生讲得很精彩,那么老师就问,他讲得好不好呀,大家听明白了吗?然后掌声鼓励,老师进行思路点拨,方法归纳;情形二,学生讲得不那么清楚,那么老师问,大家听明白了吗?学生会答,没有。那么老师有两种处理方式:方式一是再请一位同学上来讲;方式二请这个学生再讲一次,最后老师进行思路点拨,方法归纳。
在实际上课时,发生的情形是这样的:一个学生被叫上讲台,一开始,他看着大屏幕的图,背对着全班学生就要开始讲题。李老师说:“你是跟同学们说,不是和大屏幕说。”听到老师这样讲,这个学生就回过头来,低头看着讲台上电脑显示器中的图来说,李老师又说:“只有你看得见,同学们都看不见。”经李老师的这两番提示,全班学生哄堂大笑,课堂气氛似乎轻松愉悦起来了,而这位学生终也于按老师的要求,侧身指着大屏幕的图,开始讲题了。但是很显然,这位学生受到了影响,讲题时声音不大,思路也有点混乱,大家都看不出他是不是真的理解好了这道题。果然没讲好,是我们预设的情形之二。李仁康老师接下来的处理方式,让我们深受感动。学生讲完后,李老师问全班学生,大家听明白了吗?学生答,没有。只见他迟疑了一下,估计他是在想是让这个学生继续讲一次呢,还是另外叫一位学生上来讲?稍作停顿,李老师说:“这位同学可能有点紧张,我们给点掌声他,让他再讲一次。”掌声过后,李老师鼓励那位学生:“别紧张,再理一下思路。”出乎意料之外,学生成功了,这回他把解题思路讲得相当清楚,全班学生很自然地再次把掌声送给了这位学生。
二、进行学法指导,让学生“学会”讲题
案例2: 七年级几何计算题的讲题指导
对于七年级学生来说,平面几何的系统学习处于初级阶段,他们未能形成良好的解题习惯,往往知道题目怎么做,答案是多少,但是不知道该怎么规范地书写表达,更不会有条理地讲给别人听。因此,对七年级学生进行几何题的讲题指导,让他们通过讲题去理清自己的解题思路,尤为重要。如在上完北师大版数学七年级上册第四章《基本平面图形》这一单元后,实验教师就选取了下面的这道习题,对学生进行讲题方法指导。
如图 1,已知直线 AB,CD 相交于 点 O,OA 平 分 ∠EOC,∠EOC=100°,那么∠BOD 的度数是多少?

图1
对于这样一道题,很多学生确实能得到正确的答案,但大部分学生无法规范书写表达,如何突破这个问题呢?可以通过教会学生讲题,帮助学生理清答题思路。我们告诉学生讲这类题目一般有两种方法。
方法一:综合法,即由已知条件出发,一边读题一边把条件标注图上,直至把要求的角求出来。具体的方法同上面的解答过程。讲完后,进行解题反思,说一说题目所涉及的知识和方法有哪些。
方法二:分析法,即由问题出发,找到支持问题解决的所有条件。
至此,边讲边写分析过程,并告诉学生把分析的过程反过来书写,就是解答过程。
在学法指导专题讲座中,我们通过查阅相关资料,借鉴教师讲题比赛的讲题方法,运用课堂教学中出现的典型习题,对学生进行讲题指导,让学生明确讲题最重要的是和同学们分享自己的解题思路,学会该如何去讲好一道题。并让学生学习讲题的一般步骤是:1.讲题目的已知条件和问题;2.讲题目所涉及的知识点有哪些;3.讲自己想到的解题方法和解题步骤;4.讲自己在解题思路寻找过程中遇到的困难;5.讲解题后的反思。
三、把握恰当时机,让学生“乐于”讲题
案例3: 一道单元测试题的一题多解
实验教师黄老师在九年级上册第一单元的试卷讲评时,发现有一道题学生有多种解法,于是放手让学生到讲台上讲解。
题目如下:如图2,O 为矩形ABCD 对角线的交点,DE ∥AC,CE∥BD.
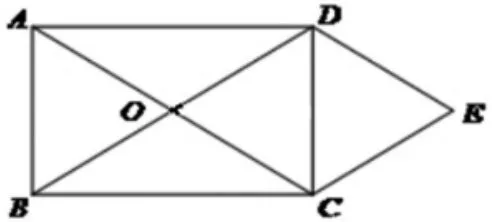
图2
(1)证明:四边形OCED 是菱形;
(2)若 AB=6,BC=8,求四边形OCED 的面积.
由于第1 问做题思路全班同学都大致相同,黄老师只要求他们讲第2 问。学生讲解如下:
生1:他一边在白板上描图(如图3),一边侃侃而谈:“我是利用菱形的面积等于两对角线乘积的一半来计算,那就要连接OE 并且求出OE,大家思考一下怎么求OE 呢?只要证明四边形OBCE 是平行四边形就行了!那么怎样证明四边形OBCE 是平行四边形呢?只要证明OB∥CE 且 OB=CE,当然,也可以证明两组对边平行。得到OE=BC=8,就可以求出菱形OCED 的面积了。”
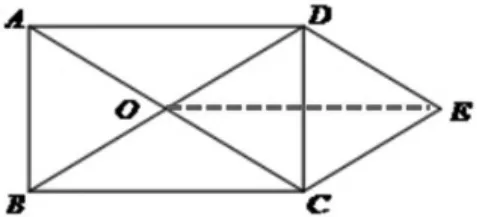
图3
老师补充了一句:从要求的面积出发,去思考还需要求出哪些边,就从哪里入手。
生2:“我也是利用菱形的面积等于两对角线乘积的一半来计算,但是我求OE 的方法不同。我认为刚刚那位同学的方法不是最优的方法,不是所有的同学都能一下反应到四边形OBCE 是平行四边形的,而且证明它是平行四边形的条件也不是那么好找。当连接OE 交CD于F 时,马上会想到OF 是ΔDBC中位线,老师经常讲第一个问题大部分是为第二个问题做服务的,这里第一问证明它是菱形,菱形的对角线互相平分就是在为第二个问题服务,这样大家很容易发现中位线从而得到 OE=8 再求出面积,是不是比他的简单呢?”
老师强调:很多时候要抓住前一个问题的证明结果或者证明思路去突破下一个问题。
生3:先在白板上将AB=6,BC=8 标在图上,“我利用的是菱形面积的另外一个公式:底×高进行计算。当我把AB=6,BC=8 标上图的时候马上想到AC=10,这就是数感,知道吗?然后就得到OC=5,OC就是菱形的底边了,能不能求出OC边上的高呢?那我们就把高DF 画出来,同学们有没有想到怎么求DF啊?原来DF 不但是菱形OCED 的高还是直角ΔADC 斜边AC 的高,利用直角ΔADC 的面积相等的办法很容易求出高,也就是×10×DF,得 DF=4.8,再求面积,我这种方法是不是比较新颖啊,比前两个同学都灵活吧!”。
老师提醒:审题要紧扣已知条件,每个已知条件能带来怎样的结果,这个结果能否成为解决问题的突破口,这都是做题的窍门。
生4:用红笔重重的在白板上把ΔODC 标出来。“我利用了矩形两条对角线把它均分成四个小三角形面积相等的方法解决这题。我们可以看到,ΔODC 的位置比较特殊,是矩形与菱形重合的部分,也就是这五个小三角形的面积都相等,那么只要求出矩形的面积问题就解决啦!
老师点拨:要关注平行四边形及特殊的平行四边形的两条对角线均分面积等等。
最后,老师试探性地又问了一次还有没有别的方法,直到没有学生举手了,老师才要求学生将这几种解题思路整理到错题本上,还布置他们继续思考,看看能不能想出新的做题思路。
“听一遍不如看一遍,看一遍不如做一遍,做一遍不如讲一遍,讲一遍不如辩一遍”,树立学生的讲题信心,教会学生讲题方法,抓住让学生讲题的良好契机,能让学生爱上讲题,爱上展示解题思维的过程,从而不断提升他们的数学表达交流素养,提高数学学习能力。

