振动辅助纳米压印制备大面积光栅结构
孙宝玉,许济琛,谷 岩,林洁琼,李 洁
(长春工业大学 机电工程学院,吉林 长春 130012)
引言
光栅结构作为一种重要的光学元件,广泛应用于光谱分析、光通信、集成光学等领域中。大量研究表明,制备单位面积内周期越小的光栅结构,明条纹越亮、越细,光栅结构具备更高的分辨率。因此,制备光栅结构中的重要研究方向,是制备出周期更小的光栅结构。目前,微米纳米制造技术高速发展,光栅结构制备工艺也有了明显进步[1]。
目前常用的光栅制备工艺主要有两类:一类是光刻技术,该技术成本过高,价格昂贵,工艺复杂且周期漫长;另一类是自组装技术,由于该技术可控性能差,在大面积制备过程中,会导致制备出的成品发生不可逆转的形变,不适合大面积批量制备[2-3]。近年来,纳米压印作为一种新型光刻技术,具备大面积、高通量、可控性高等优点,广泛应用于各种领域。葛等人通过纳米压印技术在SiNx薄膜中制备出高1.6 μm,周期4.1 μm的锥形光栅[4]。但是,仍有许多问题需要解决,如压印力不均匀,容易产生气泡,模板产生形变导致其弯曲,脱模过程中需要更大的脱模力等。另外,随着压印尺寸的增加,压印力会成倍增大,导致模具发生不可逆的形变,影响压印效果[5-7]。目前,研究人员为了解决上述问题,将振动辅助技术引入到纳米压印工艺中,超声振动是振动辅助纳米压印光刻技术中最具代表性的。Nguyen 和Park[8-9]利用数值模拟分析了超声纳米压印的机理,证明了微振动可以促进压印胶的流动并提高填充率。郑和林[10-11]研究了模具几何形状和压印聚合物厚度对纳米结构成形的影响规律,证明了振动参数对纳米结构的成型有很大的影响。振动引起的微变形和微冲击力对压印过程中纳米结构的成型具有辅助作用,由于超声波高频和大振幅难以控制,从而影响了转印图案的形貌。陈[12]等人使用振动辅助纳米压印方法提高了纳米柱结构的填充率。谷[13]等人使用振动辅助纳米压印方法有效提高了太阳能电池的转换效率。
本文提出振动辅助纳米压印方法制备光栅结构。运用时域有限差分法(FDTD),在波长300 nm~1 000 nm 范围内,数值模拟了不同光栅结构,得到了光栅结构参数变化对其吸收率的影响规律,对光栅结构进行优化,得到吸收率最佳的光栅结构,根据仿真结果优化设计模板。通过建立振动辅助纳米压印数学模型,从理论和仿真两方面验证了在压印过程中施加振动的合理性。进行振动辅助纳米压印实验,证明在实验过程中施加振动,可以有效提高填充率,改善光栅结构表面形貌,并减少缺陷。
1 光栅结构几何参数对光学性能的影响规律
1.1 仿真模型的建立
进行实验之前,研究光栅结构的周期和深宽比对光学性能的影响规律。如图1所示,使用有限差分时域法(FDTD)建立仿真模型,为了便于计算,选择了模型的单元结构进行仿真。平面尺寸(X和Y)是按照反对称边界条件设置的,沿Z方向使用完全匹配层,在微结构的上方放置反射监视器,下方放置透射监视器。模型材料选择硅,入射光选择波长300 nm~1 000 nm 的平面波光源,垂直照射到光栅表面。介电函数是使用Drude 和Lorentz模型的组合进行建模的,该模型将离散值转换为所需波长范围内的连续函数[14]。
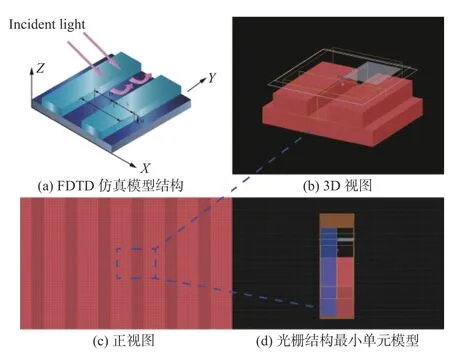
图1 光栅结构的光学设置示意图Fig.1 Schematic diagram of optical setup of grating structure in FDTD solutions
总吸收取决于反射和透射。通过(1)式获得吸收光谱A(λ):

式中:λ 是入射光的波长,T(λ)和R(λ)表示从仿真中获得的相应透射率和反射率光谱。
1.2 光栅结构深宽比变化对吸收率的影响
为了研究深宽比对光栅结构吸收率的影响规律,光栅周期取1 000 nm,占空比取0.5,深度分别取300 nm、400 nm、500 nm、600 nm,通过FDTD 数值模拟了4 种光栅结构的吸收率随波长的变化规律。光栅结构的吸收率趋势是随着波长的增加而降低的,如图2所示。波长300 nm~400 nm 区间内,吸收率变化并不明显,这是因为波长较短时,散射较弱,大量光被反射到空气中,没有被光栅结构吸收。波长400 nm~500 nm 区间内,吸收率是先增大后减小,波长475 nm 处达到最大值。波长500 nm~800 nm 区间内,吸收率随波长增加明显下降。硅材料自身在长波长频段固有的低吸收系数,尽管引入光栅结构,极大程度地提高了吸收率,但是受到硅材料自身限制,仍不可避免地导致吸收率曲线急剧下降。波长800 nm~1 000 nm 区间内,吸收率呈现降低趋势,但是趋势缓慢,大量的光穿透到光栅结构中没有被光栅结构吸收、反射。光栅结构的吸收率随着光栅结构深度的增加而增大,随着深度的增加,大量的光在狭缝中多次反射,得到了更好地吸收利用。
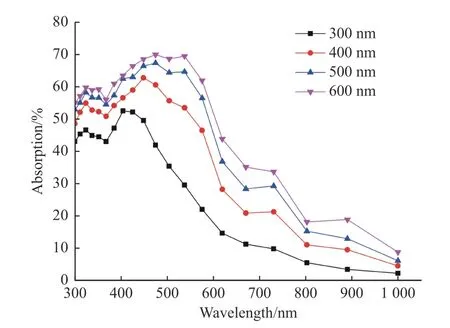
图2 光栅结构深宽比不同时吸收率随波长的变化曲线Fig.2 Variation curves of absorptivity with wavelengths for different depth-to-width ratio of grating structure
1.3 光栅结构的周期变化对吸收率的影响
当光栅结构周期一定时,深度越大的光栅结构,具有更好的光吸收性能。为了研究周期变化对光栅结构吸收率的影响规律,光栅结构的深度取600 nm,占空比取0.5,周期分别取1200 nm、1400 nm、1600 nm、1800 nm。通过FDTD 数值模拟了4 种光栅结构的吸收率随波长的变化规律。
光栅结构的吸收率整体趋势是随着波长的增加而降低的,如图3所示。随着单位面积内周期的减小,吸收率也逐渐增加。光栅深度相同时,单位面积内周期越小,周期越多,对光的吸收利用能力就越强,吸收率也就越高。当周期为1 200 nm,深度为600 nm 时,吸收率最高可以达到70%。

图3 光栅结构周期不同吸收率随波长的变化曲线Fig.3 Variation curves of absorptivity with wavelengths for different grating structure period
通过研究光栅结构周期和深宽比参数的变化,得到了对吸收率的影响规律。选择制备周期为1 200 nm,深度为600 nm,占空比为0.5 的光栅结构作为实验模板。
2 振动辅助纳米压印机理研究
在研究图案转移过程中,将填充材料堆积到模板腔体内的填充程度,作为衡量压印质量优劣的一个重要指标,因此,提高填充率是改善压印后微结构性能的重要途径之一。压印过程中,压印材料填充模板时,压印材料和模板之间的相互作用力,以及压印材料处于半凝固态时对模板产生的阻力,都会导致所需的机械力变大,填充时间变长,从而降低填充率。针对上述问题,在压印过程中,引入由压电驱动的横向一维振动,在压印材料填充模板的过程中,施加低频率低振幅的振动,相当于在填充过程中施加了一个横向的力,减小了填充过程中压印胶产生的摩擦阻力,从而增大了压印产生的机械力,使得压印胶更好地填充进模板中。
2.1 建立振动辅助纳米压印原理数学模型
为了研究引入横向振动的合理性,建立了压印过程中施加振动的数学模型,如图4所示。为了简化模型,忽略了梁结构的弹性变形,假设压印胶的流体流动符合牛顿流体特征,且粘度不随时间变化发生改变。

图4 振动辅助纳米压印机理数学模型图Fig.4 Mathematical model of vibration-assisted nanoimprint mechanism
通过Young-Laplace 方程可以得出液-气界面上的压差为[15-17]

式中:γ是压印胶的表面张力;r1和r2是曲率半径;P0是压印胶中的压力;Pi是气阻界面上的压力,并且假定在压印胶填充过程中气压P0是恒定的。

式中,θ是压印胶与模板的接触角。

通过Lucas-Washburn 方程从Poiseille 中推导出压印胶的填充上升过程为[18]
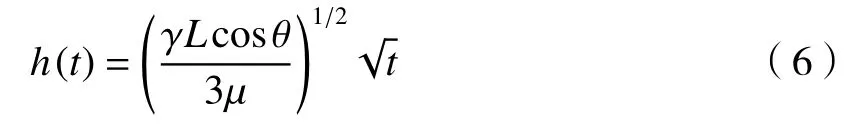
压印胶表面力引起模具梁发生弹性变形,压印胶表面力导致的应力分布在梁内部,与梁上的压差相对应。惯性的动量为

式中,H是梁的高度,横截面的弯曲动量为

假设梁上的压力差引起梁上的载荷是均匀的,则有:

根据弹性梁弯曲模型,横穿梁的应力为
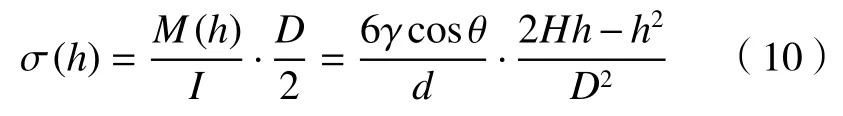
最大值出现在h=H处,可用以下公式估算:

在往复运动中,施加一个振动周期是T,撞击微结构侧壁的时间是Δt,则撞击周期是T→T+Δt。由于规则的频率振动,Δt可以被认为是一个常数。假设压印胶的等效质量为M。根据脉冲定理,冲击力为

由于冲击力使实际应力 σt已经改变,则:

从数学建模的角度,证实了在压印过程中引入横向一维振动的合理性。有助于增大压印需要的机械力,使压印材料更好地填充模板腔体中。
2.2 振动参数对填充率的影响规律
通过建立振动辅助纳米压印数学模型的方法,验证了在压印过程中施加振动的合理性。进一步研究在压印过程中施加振动对填充率的影响,讨论了振动参数对填充率的影响规律。选择周期为1 200 nm,深度为600 nm,占空比为0.5 的光栅结构作为研究振动参数对填充率关系的仿真模型。
2.2.1 振动频率对填充率的影响规律
通过仿真软件进行仿真分析,得到了振动频率和填充率的关系,如图5所示。在振幅不变时,随着振动频率的增加,填充率随着增加,并没有大幅度增加。当输入振幅为100 nm 时,输入振频为25 Hz,填充率为75%,振频增加到250 Hz 时,填充率随着增加到76%,填充率仅增加了1%。输入振幅不变时,振频对填充率的影响很小。增加振频只是增加了单位时间内压印胶接触光栅侧壁的次数,并没有改变压印力。
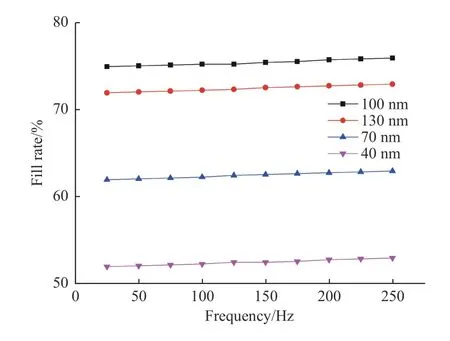
图5 填充率随振动频率变化曲线Fig.5 Variation curves of filling rate with vibration frequency
2.2.2 振动幅度对填充率的影响规律
对振动频率和填充率的关系进行仿真分析,得到250 Hz 的振频有助于提高填充率。固定振动频率为250 Hz,振幅和填充率的关系如图6所示。随着振幅的增加,填充率先增大后减小,当振幅在100 nm 左右时,填充率达到最大值76%。振动引起的微振幅和微位移增加了压印胶与光栅结构侧壁的接触面积,增大了压印胶在侧壁上的滑动距离,使更多的压印胶流入空腔内。振幅大于100 nm时,填充率呈现下降趋势。过大的振幅使已经填充进光栅结构空腔内处于准凝固状态的压印胶发生不可逆的形变,降低了填充率,破坏了光栅结构的形貌。
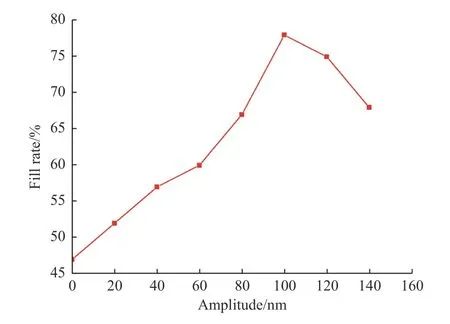
图6 填充率随振动幅度变化曲线Fig.6 Variation curve of filling rate with vibration amplitude
3 振动辅助纳米压印实验
3.1 压印模板的制备
压印硅模板的制备过程可描述如下:在超声波浴中用丙酮和酒精溶液对硅基片进行清洗15 min,用氮气吹干;蒸镀一层20 nm 金属Cr 薄膜在硅基板表面,采用匀胶机旋涂电子束光刻胶在金属Cr 膜上;利用电子束直写系统曝光直写光刻胶表面,光刻胶显影后形成微结构图案;采用干法刻蚀刻蚀金属薄膜Cr;清洗表面残余光刻胶后,采用干法刻蚀刻蚀硅基板;最后,在硅基底上得到光栅结构的硬模板[19]。将PDMS 旋涂在硅基板上,并加热到其玻璃化转变温度(Tg)。将周期性纳米结构的硬模具应用到PDMS 上,并压缩到有限的数量,在该位置保持一定的保温时间,温度降低到玻璃化转变以下,随着PDMS 继续冷却,硬模被移除,光栅结构被转移到PDMS 模板上。为了模拟结果与实际制备相匹配,选择PDMS 模具周期为1 200 nm、深度约为600 nm 的光栅结构作为实验的主模板。
3.2 振动辅助纳米压印制备过程
纳米压印工艺实施的首要条件是对模板与衬底表面进行清洗,对模板表面进行抗粘连处理。振动辅助纳米压印流程图如图7(a)所示。在主模上使用IMCS 溶液作为抗粘涂层,通过气相沉积法形成一层抗粘连层。在处理完主模后,选择厚度为0.5 mm 的硅模板作为衬底。压印胶旋涂之前,在超声波浴中用丙酮和乙醇溶液清洗硅模板,用去离子水冲洗并干燥。硅模板在120 ℃的烤箱中烘烤5 min,在旋涂前冷却至室温。经此处理后,将硅模板表面的杂质清除干净,使压印胶能够附着在硅模板表面。实验中选择一种负型光刻胶(NIP-010)作为压印胶,以3 000 rpm 的速度将压印胶旋涂在硅模板表面,旋涂时间为20 s。将旋涂好的硅模板放置在80 ℃的烤箱中烘烤30 s,使压印胶更好地附着在硅基板上。随后,将硅模板放在振动辅助纳米压印装置上面进行实验,如图7(b)所示。通过压电驱动的微动平台,在压印过程中施加频率为250 Hz,振幅为100 nm 的一维振动。
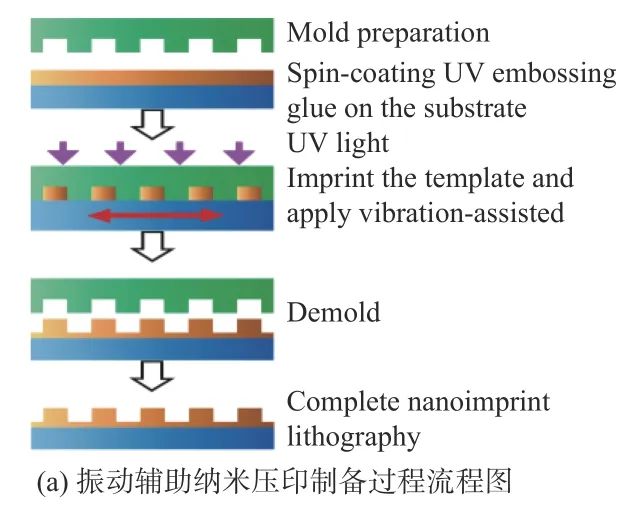

图7 振动辅助纳米压印制备过程示意图Fig.7 Schematic diagram of preparation process of vibration-assisted nanoimprint
3.3 结果与讨论
为了研究振动辅助纳米压印和传统纳米压印的区别,设计了对比实验。如图8(a)所示,在不引入振动的情况下,光栅结构发生粘连,周期间发生错位现象,因为当光栅结构尺寸足够小时,压印力不够大,导致了模板发生形变。如图8(b)所示,引入振动后,提高了压印质量,减少了缺陷发生。
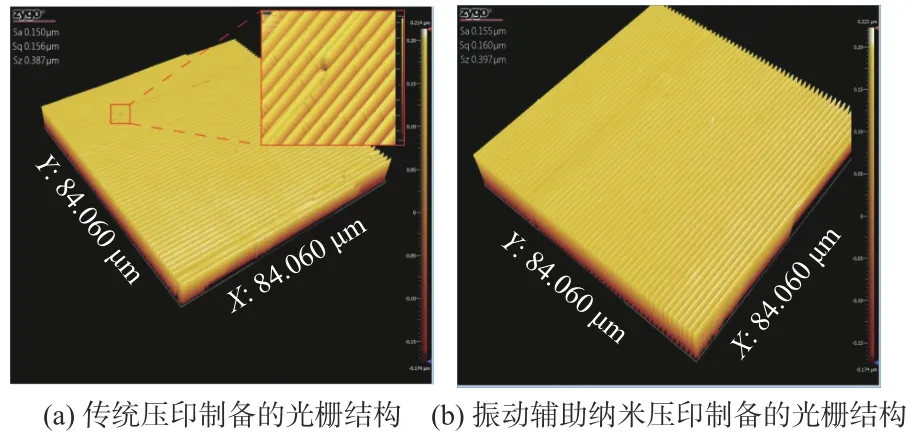
图8 ZYGO 表面形貌图Fig.8 ZYGO surface topography diagram
图9 为振动辅助纳米压印方法加工出来的光栅结构,通过SEM 图可以明显看到,引入振动后,加工出来的光栅结构表面平整、规则,具有很高的表面质量和良好的表面形态。

图9 光栅结构的SEM 检测图Fig.9 SEM detection diagram of grating structure
为了直观地比较填充率,通过多点观察获得了光栅结构的平均高度和宽度,如图10所示。通过曲线可以明显看到添加振动后,平均填充高度增加了约30%。
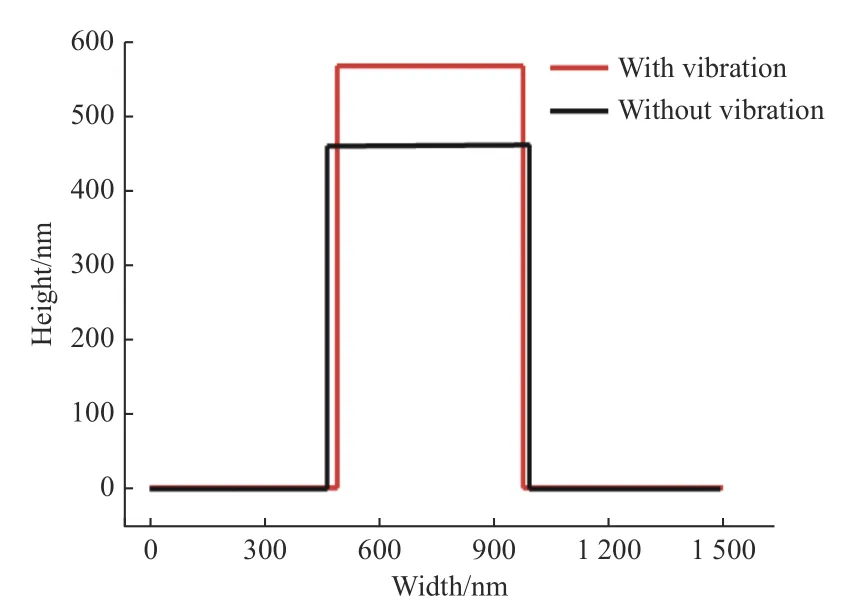
图10 通过多点观察得到光栅结构的平均高度和宽度Fig.10 Average height and width of grating structure obtained by multi-point observation
4 结论
本文提出了一种新型振动辅助纳米压印方法,用来制备大面积光栅结构。对模板参数进行优化,得到光栅结构参数的改变对吸收率的影响规律。通过对振动辅助纳米压印理论分析和实验研究,得到以下重要结论:1)提出了一种新型振动辅助纳米压印方法,用来制备大面积光栅结构,通过在压印过程中施加横向低频、低振幅振动,增大了压印力,从而减少了压印时间,提高了填充率;2)通过FDTD 对光栅结构进行光学性能仿真,研究了光栅结构参数对吸收率的影响规律,当光栅结构周期为1200 nm,深度为600 nm 时,吸收率可以达到70%;3)通过振动辅助纳米压印实验,对比了振动辅助纳米压印和传统纳米压印的实验效果,证实了在纳米压印过程中施加振动,有助于提高填充率,与传统纳米压印相比,压印胶的填充率提高了30%,并改善了压印后微结构的表面形貌。

