隧道竖井出渣孔孔径的确定及其稳定性分析
冉华,段兴明,魏通,尹定鹏
(1.云南交投公路建设第一工程有限公司,昆明 650034;2.重庆交通大学土木工程学院,重庆 400074)
公路隧道竖井的开挖方式可以分成正井法和反井法,二者的区别在于是否开挖一定直径的导井,同时两者比选的前提条件是竖井下部的主隧道是否已经建成。正井法是从井口位置从上往下全断面开挖,在井口位置设置井架和提升设备用于升降多层操作平台供施工人员和仪器设备进出,同时进行出渣和排水。对于较深的竖井而言,正井法工期较长,排水不便,出渣效率低,仪器设备使用复杂繁琐且工作量增加,成井较慢,施工期间安全性较差,存在安全隐患。反井法则利用已开挖好的导井出渣,施工及出渣效率高,仪器设备使用便利,对周边环境影响较小,节约成本。在竖井反井法施工的整个过程中,出渣孔的稳定性尤为重要,期间一旦发生出渣孔失稳破坏、塌陷堵孔等问题,将会对整个竖井工程带来较大影响,故针对竖井反井法的施工研究是很有必要的。
目前针对竖井反井法的研究成果有很多。赵顺义等[1]结合杭州市紫之隧道工程土建第Ⅱ标段1#竖井与2#竖井工程,对竖井爆破开挖、支护施工等进行了优化。孙臣生[2]依托山西省五台山—盂县高速公路藏山隧道竖井工程,通过对比正井法和反井法施工,得出反井法施工具有占地较少、环境影响较小的优点。杨继华等[3]研究了厄瓜多尔科卡科多辛克雷(Coca Codo Sinclair, CCS)水电站超深竖井工程,分析了反井法施工中存在的问题,分析成因,同时提出相应解决方案。程守业[4]以敦格铁路当金山隧道竖井为例,对反井法进行改进,提出反井法施工中的导向孔偏斜控制措施。陈光明等[5]结合3座特长公路隧道斜井、竖井的施工方案比选,表明反井法施工能够节约劳动力、经济成本。于见水等[6]对反井钻机偏斜机理进行分析,对类似的工程具有指导意义。苗栋等[7]对CCS水电站2#竖井坍塌事故进行分析,分析事故原因,并得出解决方案及相应的加固措施。李忠[8]以福州京台高速公路牛岩山隧道竖井工程为例,发现反井法能够避免常规降挖法和爬升机工法的不足,在保证施工安全的前提下提升工程效率和质量。王彬彬[9]以通省隧道2#通风深竖井为研究对象,对竖井反井法施工中的导向孔纠偏控制以及反井法反向扩孔和程序转换进行了说明。王春玲[10]对反井钻机法在竖井施工中的应用进行研究,对不良地质下的钻孔施工情况下的解决措施进行了阐述。
以上研究分别是针对正井法和反井法的方案比选、反井法施工优势及优化、反井法施工中存在的问题、导向孔纠偏控制以及竖井坍塌的解决措施,但是针对竖井出渣孔的孔径选择及其稳定性研究较少,由于云南省墨江至临沧高速公路泰和隧道竖井是深竖井,能否采用无支护的出渣孔及其孔径的选取,设计和施工不能确定,因此有必要对泰和隧道竖井工程出渣孔孔径选取及其稳定性进行分析研究。
1 工程概况
云南省墨江至临沧高速公路泰和隧道左幅和右幅正常运营工况采用全射流纵向通风方式,消防排烟工况采用竖井分段排烟方式,于隧道右线K203+408两幅隧道正中间设置一座排烟竖井,竖井中心坐标(x=511 166.983 2,y=2 644 853.358 0),设计内轮廓直径5.0 m,设计深度279.55 m,竖井内径5.0 m。
根据地勘报告提供的成果,将竖井围岩划分为Ⅴ1、Ⅳ3、Ⅳ2围岩级别,竖井深0~20 m段为Ⅴ1级围岩,占7%;竖井深20~50 m段为Ⅳ3级围岩,占11%;竖井深50~279.55 m段为IV2级围岩,占82%。
本竖井井身段采用钻机反井正向扩挖法施工,先用天井钻机在井位中心从上到下钻导向孔,直达联络通道顶,待井下联络通道与竖井贯通后,在隧道中拆除钻头,换成扩孔刀头,由下而上,扩成一定直径的天井(出渣孔)与联络通道连通,最后再用钻爆法从上往下扩挖到设计尺寸,炮渣直落井底,装载机装渣,自卸汽车运送至弃渣场弃渣。
竖井井架提升结构、人员设施上下吊桶分别如图1、图2所示。根据《泰和隧道工程工程地质勘察报告》提供的勘察实测数据和《公路隧道设计规范》(JTG 3370.1—2018)提供的相应参考值,并考虑到水、断层和裂隙等不良地质情况做了相应折减到70%后进行综合确定。计算参数如表1所示。

图1 井架提升结构

图2 人员设施上下吊桶

表1 岩土力学参数
2 竖井出渣孔孔径大小及其稳定性分析
隧道竖井出渣孔深长细直,其孔径的选择应当考虑多方面因素。结合围岩地质情况以及工程实际需求,选定合理经济的出渣孔孔径十分必要。出渣孔直径过大,虽然利于出渣,但是无支护出渣孔自身稳定存在问题;出渣孔直径过小,能够使无支护出渣孔自身稳定,但是出渣的效率会大大减小。针对出渣孔不同直径进行分析研究,选取出渣孔直径分别为1.0、1.2、1.4、1.6、1.8、2.0 m共计6种工况进行对比分析,如表2所示。

表2 不同直径出渣孔分析工况
2.1 理论分析方法
对于完整、均匀、坚硬的岩体,在分析围岩的应力和位移或者评定围岩的稳定性时,可以采用弹性力学的方法。对于成层的和节理发育的岩体,如果层理或节理等不连续面的间距与所研究的问题的尺寸相对较小时,则连续化假定和弹性力学的方法仍然适用。
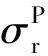
塑性区围岩径向应力的计算公式为
(1)
塑性区围岩切向应力的计算公式为
(2)
塑性区半径的计算公式为
(3)
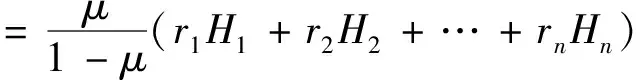
(4)
式中:μ为岩土体的泊松比;c、φ分别为岩土体的黏聚力、内摩擦角;r为任一点半径;r0为圆洞半径;γi为分层岩土体重度i=1,2,…,n;Hi为分层岩土体高度,i=1,2,…,n;P为水平应力,P=3 426.56 kN/m2;Pi为支护抗力,由于本计算是考虑无支护的出渣孔的围岩压力与变形的情况,故Pi=0。
进而式(1)~式(3)修改如下。
径向应力的计算公式为
(5)
切向应力的计算公式为
(6)
塑性区半径的计算公式为
(7)
塑性区域内的径向位移的计算公式为
(8)
式(8)中:σz为初始应力场。
松动区是指塑性圈内圈应力低于初始应力的区域,松动区半径的表达式为

(9)
经过理论分析计算,得出不同直径下竖井围岩径向、切向应力随着远离中心点的变化情况,以及围岩最大水平位移、塑性区半径随着不同直径的变化情况。塑性区径向应力随r变化规律如图3所示,塑性区切向应力随r变化规律如图4所示,水平位移随r变化规律如图5所示,塑性区半径变化如图6所示。

图3 理论分析塑性区径向应力随半径变化规律
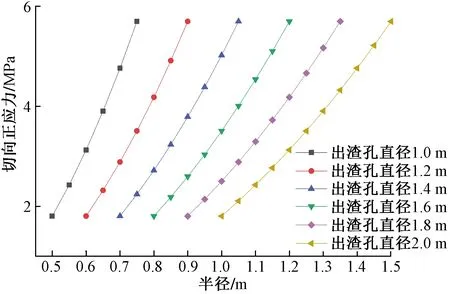
图4 理论分析塑性区切向应力随半径变化规律

图5 理论分析水平位移随半径变化规律

图6 理论分析塑性区半径变化
径向应力随r变化规律如图3所示,可以看出,不同孔径下,半径为1/2孔径处的径向应力为0,随着所求点半径的增大,径向应力逐渐增大,当r达到塑性区半径时,径向正应力为1.196 MPa。
切向应力随r变化规律如图4所示,可以看出,不同孔径下,半径为1/2孔径处的切向正应力为1.804 MPa,随着所求点半径的增大,切向应力逐渐增大,当r达到塑性区半径时,切向正应力为5.696 MPa。
水平位移随r变化规律如图5所示,随着出渣孔直径的增大,围岩最大水平位移增大;出渣孔直径由1.0 m增加到2.0 m时,围岩的最大水平位移相应的由3.437 mm增大到6.874 mm。
塑性区半径随出渣孔直径变化规律如图6所示,塑性区半径随着出渣孔直径的增大而增大,出渣孔直径由1.0 m增加到2.0 m时,塑性区半径相应的由0.75 m增大到1.5 m。
2.2 数值分析方法-平面轴对称模型
利用大型有限元软件ANSYS建立有限元数值模型进行模拟分析时,均采用PLANE42单元,模拟时设置为轴对称单元。模型计算范围为长×高=130 m×279 m,左侧竖井开挖单元总宽度为出渣孔的半径。荷载仅考虑自重;岩土层采用弹塑性材料,本构模型采用服从D-P准则的弹塑性模型;假定岩层为水平分层,根据地质图,各岩层的厚度根据不利原则取不利岩层的最大厚度;有限元分析过程中的岩土体全部为均质连续体,忽略实际岩体中的节理裂隙问题;X轴方向的两侧边界约束X方向位移,底部边界约束Y方向位移,上部边界为自由面。有限元计算模型中划分的单元网格数量为9 782。模型具体物理参数取值如表1所示。最终网格划分如图7、图8所示。

图7 有限元网格模型

图8 有限元网格模型岩层
2.3 数值模拟结果分析
由于篇幅所限,仅给出直径1.4 m出渣孔情况下的数值分析结果。
2.3.1 出渣孔围岩应力结果分析
直径1.4 m出渣孔工况下的围岩第一主应力如图9、图10所示,围岩第三主应力如图11、图12所示,围岩塑性区如图13所示。不同工况下数值分析塑性区半径变化如图14所示,第三主应力随r变化规律如图15所示。
图9 围岩第一主应力
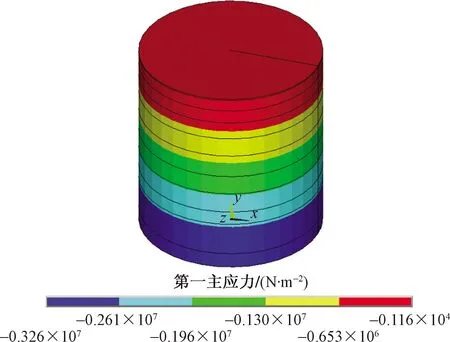
图10 围岩第一主应力二维轴对称扩展图
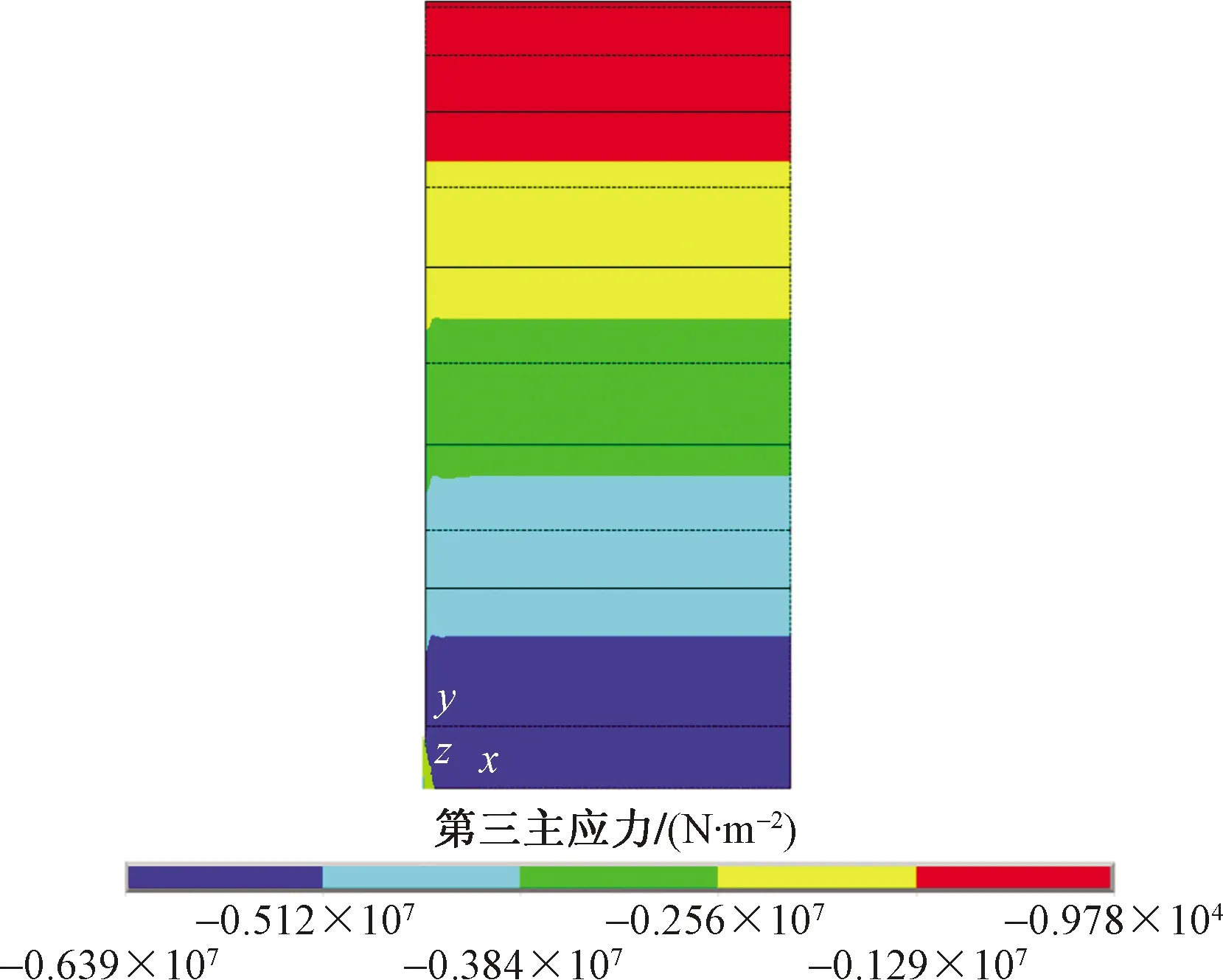
图11 围岩第三主应力
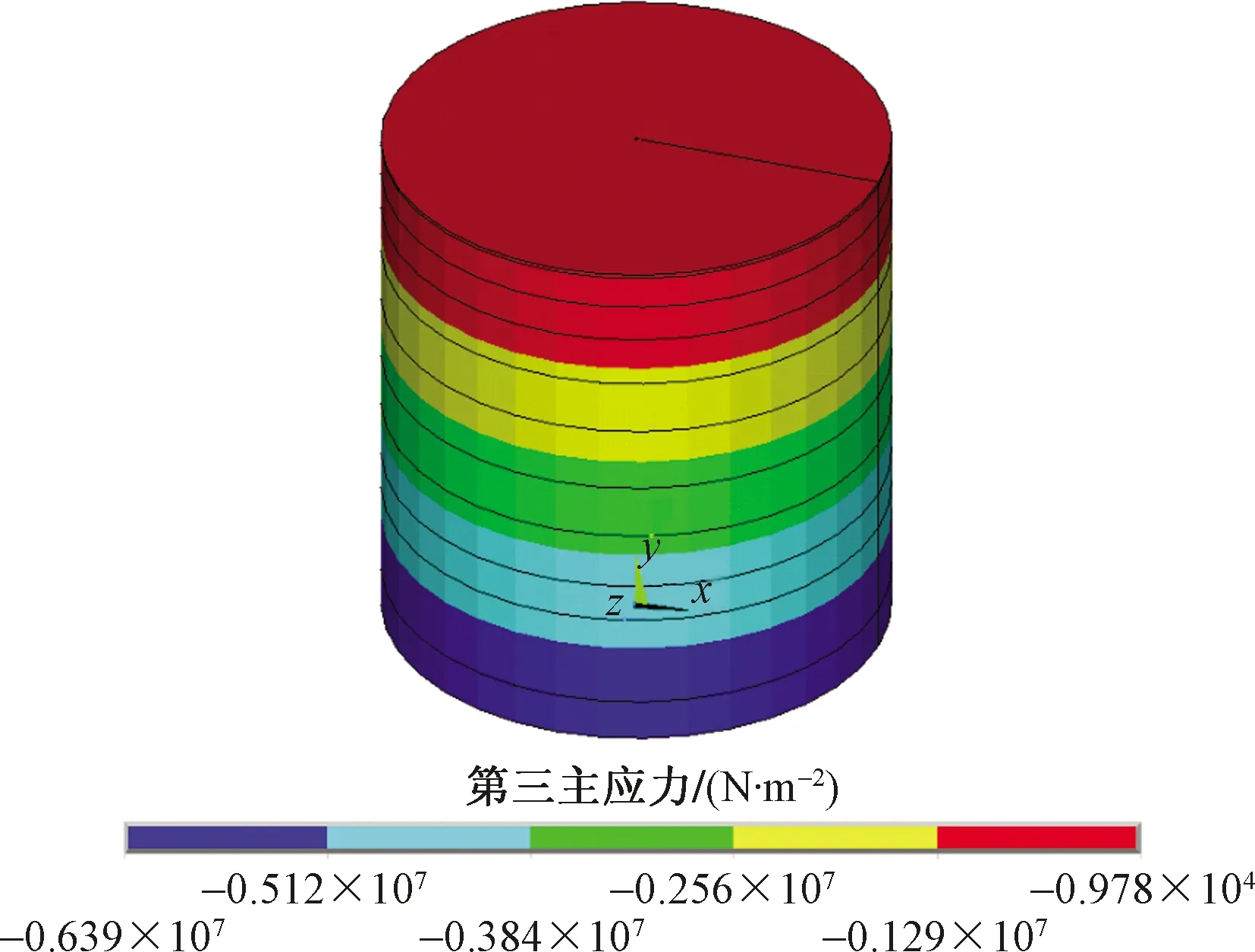
图12 围岩第三主应力二维轴对称扩展图
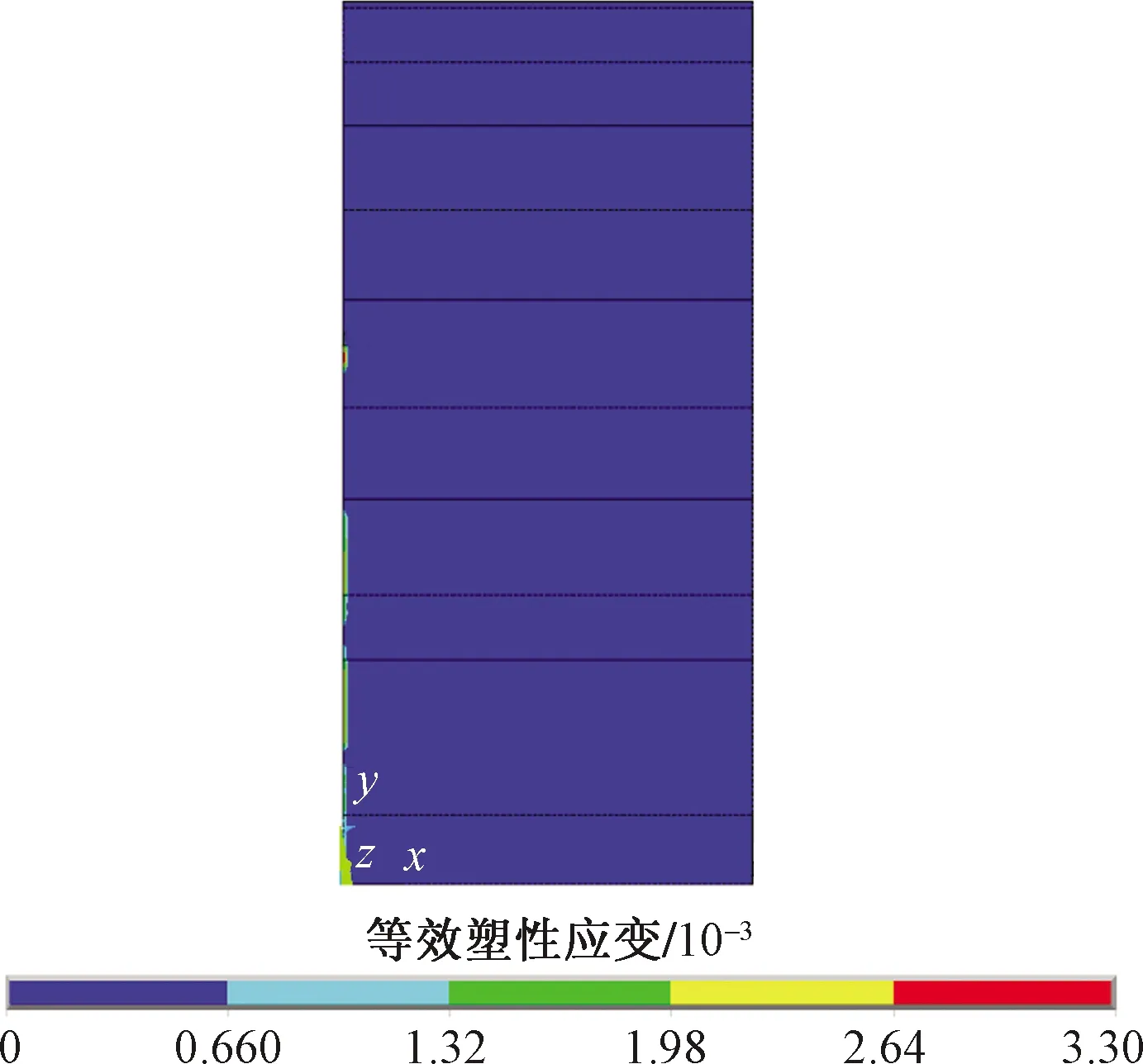
图13 围岩塑性区

图14 数值模拟塑性区半径变化
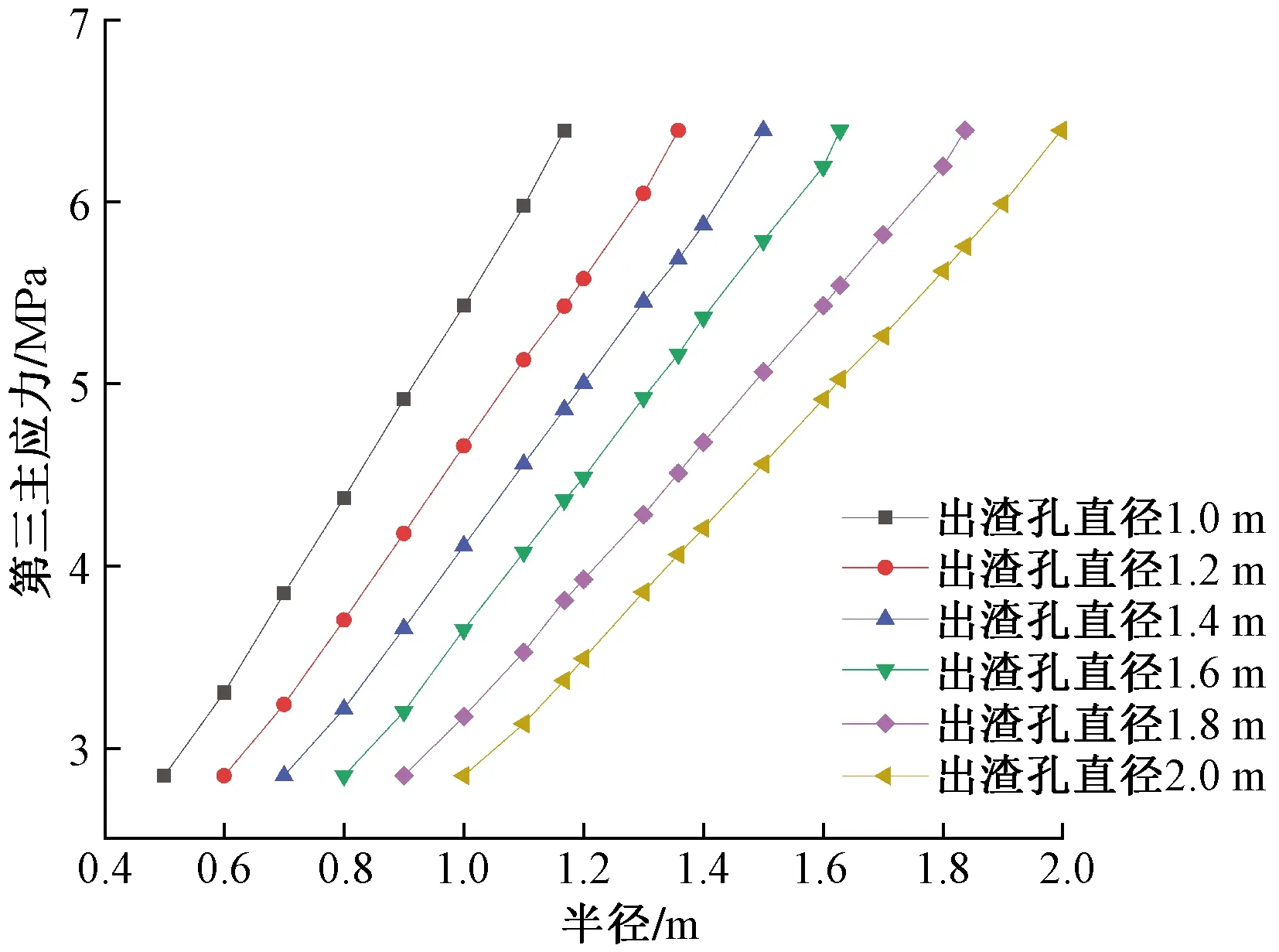
图15 数值模拟第三主应力随半径变化规律
由以上数值模拟分析可知:①数值模拟分析塑性区半径随出渣孔直径变化规律如图14所示,塑性区半径随着出渣孔直径的增大而增大,出渣孔直径由1.0 m增加到2.0 m时,塑性区半径相应的由1.168 m增大到1.997 m;②数值模拟分析第三主应力随r变化规律如图15所示,可以看出,随着所求点半径的增大,径向应力逐渐增大,当r达到塑性区半径时,第三主应力绝对值为6.390 MPa。
2.3.2 出渣孔围岩变形结果分析
直径1.4 m出渣孔工况下的围岩竖向位移如图16、图17所示,围岩水平位移如图18、图19所示。不同工况下数值分析水平位移随r变化规律如图20所示。

图16 围岩竖向位移
图17 围岩竖向位移二维轴对称扩展图
图18 围岩水平位移

图19 围岩水平位移二维轴对称扩展图
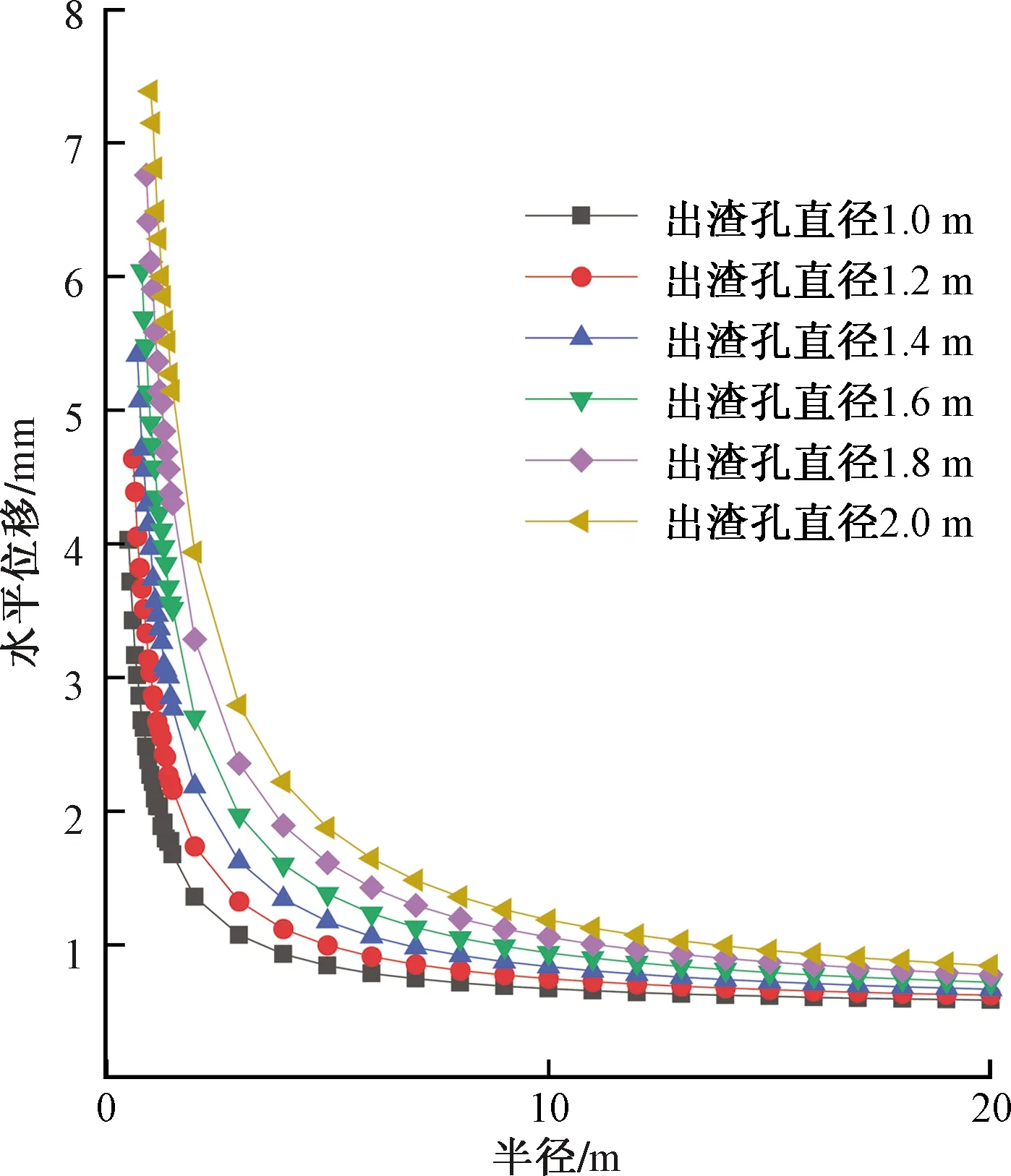
图20 数值模拟水平位移随半径变化规律
由数值模拟分析围岩变形结果可见:①不同工况数值模拟分析水平位移随r变化规律如图21所示,随着出渣孔直径的增大,围岩最大水平位移增大;出渣孔直径由1.0 m增加到2.0 m时,围岩的最大水平位移相应的由3.987 mm增大到7.474 mm;②在直径1.4 m出渣孔开挖过程中,由于荷载释放效应,围岩向竖井内部变形,导致周边围岩发生轻微的变形;③出渣孔直径1.4 m,周边围岩累计最大水平位移量为5.412 mm,累计最大竖向位移量为0.631 mm,并未超过允许值,风险可控;④在开挖直径1.4 m出渣孔施工过程中,围岩变形可控,围岩稳定。
2.4 理论分析与数值模拟对比分析
将理论分析与数值模拟结果进行对比分析,如表3所示。
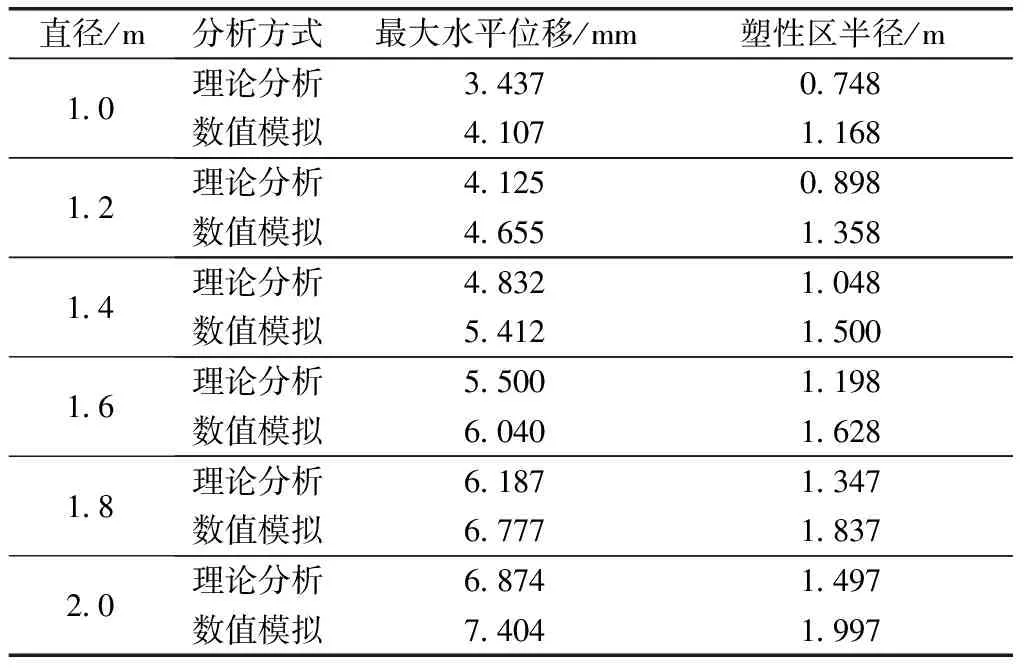
表3 理论分析与数值模拟结果对比
结合以上分析,考虑到随着出渣孔直径的增大,塑性区半径以及最大水平位移均增大,出渣孔的安全孔径不应大于1.4 m,当超过该孔径时,围岩的最大水平位移以及塑性区较大,不能保证出渣孔的稳定性;同时结合工程实际,出渣孔的直径不宜太小,否则会影响竖井施工过程中的出渣效率,综合考虑之后,选择出渣孔直径为1.4 m是合理的。
通过理论分析计算与有限元数值模拟结果对比分析,从围岩水平位移以及塑性区半径比较可知,表明泰和隧道竖井可采用直径1.4 m的出渣孔,且出渣孔整体稳定。
3 现场观察状况
根据现场实际观察状况,泰和隧道竖井直径1.4 m出渣孔未发生大变形,出渣孔成孔较好,在整个施工的过程当中没有出现失稳破坏、塌陷堵孔等问题,出渣孔整体稳定,保证了竖井的顺利施工。表明理论公式和有限元数值计算是基本准确的,能够指导设计和施工。出渣孔底部如图21所示。

图21 出渣孔底部
4 结论
(1)经过理论分析,泰和隧道竖井直径1.4 m出渣孔的围岩应力、位移数值上均处于可控范围之内,竖井出渣孔整体稳定;
(2)经过有限元数值计算分析,隧道竖井直径1.4 m出渣孔整体稳定,可不对出渣孔进行加固。
(3)结合现场实际观察,隧道竖井出渣孔变形较小,未出现失稳破坏。

