EJ299-33A闪烁体光输出及其应用研究

王德鑫 张苏雅拉吐 胡新荣 任 杰 红 兰 王金成, 宋 娜王宏伟 黄美容 唐 鑫 立 立 白嘎拉 牛丹丹

1（内蒙古民族大学数理学院 通辽 028000）

2（内蒙古民族大学核物理研究所 通辽 028000）

3（中国科学院上海应用物理研究所 上海 201800）

4（中国原子能科学研究院核数据重点实验室 北京 102413）

5（呼伦贝尔学院物理与电子信息学院 海拉尔021008）

6（沈阳师范大学物理科学与技术学院 沈阳 110034）

上海激光电子γ源（Shanghai Laser Electron Gamma Source，SLEGS）是上海光源二期线站建设的主要部分之一，它可以提供强度和极化度高，单色性和方向性好高品质的γ束，可用来开展基础研究和应用研究。基础研究方面，主要针对核天体物理中p-process（p过程和p nuclei）、s-process（慢中子俘获过程）、r-process（快中子俘获过程），以及先进核能系统设计相关的光核反应出射中子核数据测量研究［1−2］，迫切需要设计与研发一套合适的中子谱仪。BC501A、NE213及EJ301型液体有机闪烁体常用于中子探测实验中。然而，液体闪烁体存在容易起泡、包装复杂、很难长时间保存以及低探测密度等问题，在一些特殊实验环境和实验测量中很难应用。Eljen Technology公司生产了一款新型塑料固体闪烁体EJ299-33A［3］，因 具有脉冲形状甄 别（Pulse Shape Discrimination，PSD）本领、发光衰减时间快、探测密度大以及容易加工和保存等优点，可用于伴有较强γ射线本底的中子探测实验中，进行精确的n-γ事件分辨［4−5］。塑料闪烁体对电子能量响应函数为线性，而对质子及其他带电粒子的响应函数为非线性［6−7］。实际工作中，常利用标准γ射线光输出谱得到探测器电子能量线性和能量分辨率，并进一步研究其中子探测阈、探测效率及权重函数等问题［8−13］。本文利用多道脉冲幅 度 分 析 器（Multi-Channel pulse amplitude Analyser，MCA）与EJ299-33A塑料闪烁体搭建一套探测器与电子学数据获取系统，实验测量137Cs、60Co标准γ源对探测器的光输出谱。同时，采用欧洲核子研究中心（CERN）开发的Geant4模拟软件包对EJ299-33A塑料闪烁探测器的光输出进行模拟，并根据实验数据对其进行了能量分辨展宽。通过对比实测光输出谱与模拟结果，深入研究了EJ299-33A塑料闪烁体探测器的电子能量线性，中子探测阈及权重函数。同时，对不同的入射能量的γ光输出谱进行分析，计算出了EJ299-33A塑料闪烁体能谱-剂量函数，并与理论计算结果进行了比较。

1 实验测量

探测器γ响应函数在中子探测实验中具有十分重要的意义，其结果直接影响实验数据的准确性。本次实验在内蒙古民族大学核物理研究所核探测实验室大厅内，利用标准γ放射源60Co和137Cs测量了EJ299-33A塑料闪烁体的γ光输出谱。实验具体探测器与电子学示意图如图1所示，标准γ源放在探测器中心线距离窗口0.1 cm位置。EJ299-33A闪烁体尺寸为Ø5.08 cm×5.08 cm，密度是1.08 g·cm−3。探测器加上高压后光电倍增管阳极输出的电信号经过主放大器ORTEC672放大和高斯成形再进入多道脉冲幅度分析器进行采样获取数据并存入计算机。通过实验测量，得到了标准60Co和137Cs源的光输出分布谱，在相同条件下也测量了实验室环境本底，并在离线数据分析中进行了扣除。使用欧洲核子中心开发的面向对象的ROOT软件包进行离线数据分析。

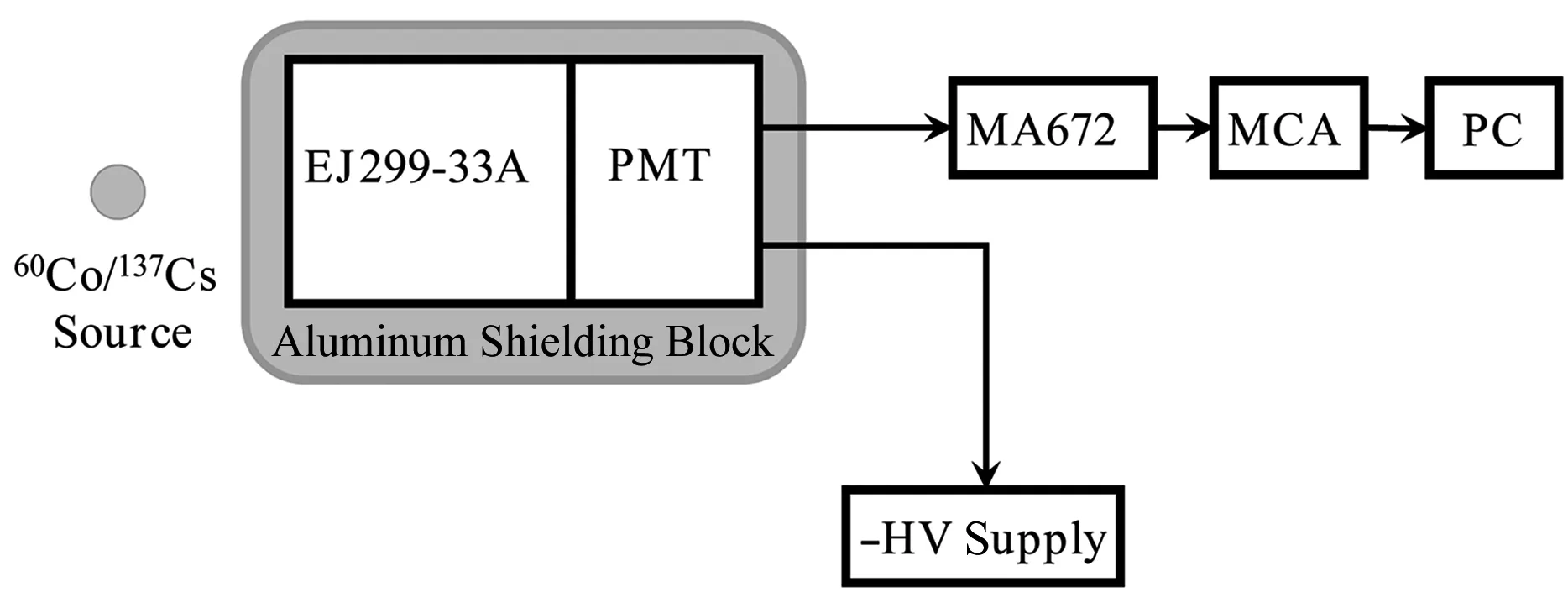
图1 探测器与电子学示意图Fig.1 Schematic diagram of detector and electronics

2 蒙特卡罗模拟程序

Geant4是由欧洲核子研究中心开发的基于面向对象编程语言C++的蒙特卡罗模拟程序软件包，因具有可视化、粒子追踪及可处理复杂几何体等优点，被广泛用于核物理与粒子物理实验中模拟粒子输运和粒子与物质相互作用过程。Geant4模拟计算中建立的探测器模型与实验中所采用的一样，EJ299-33A塑料闪烁体的化学成分为H和C，密度为1.08 g·cm−3，每立方厘米含有5.13×1022个氢原子、4.86×1022个碳原子和3.55×1022个电子，塑料闪烁体是底面直径为5.08 cm、高度为5.08 cm的圆柱体，在闪烁体外裹有0.5 mm厚的铝壳。具体探测器结构与Geant4计算模型如图2所示，探测器的各组分与其化学成分相应比例如表1。本工作中，使用Geant 4.10.05版本和标准的电磁物理相互作用和新的数据集G4EMlow.7.7研究γ射线、电子与物质相互作用过程。

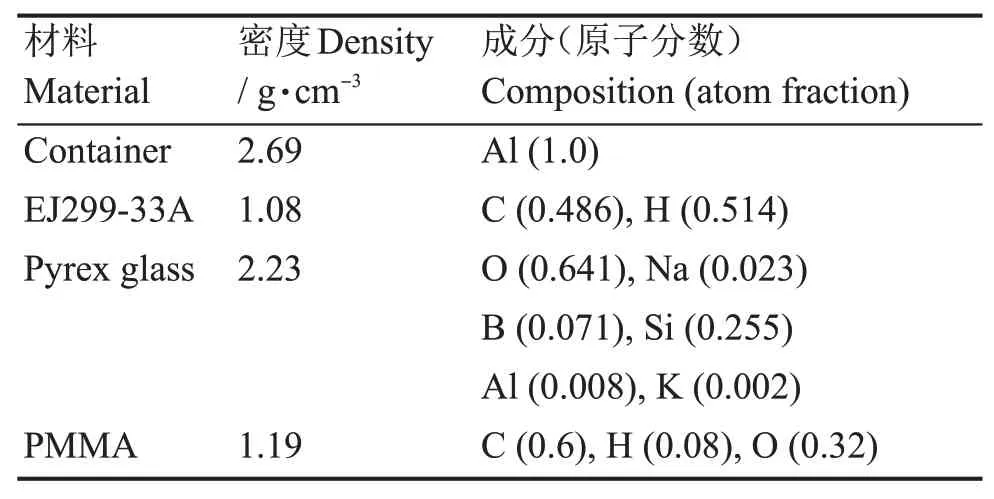
表1 EJ299-33A探测器的化学成分Table 1 Chemical composition of EJ299-33A

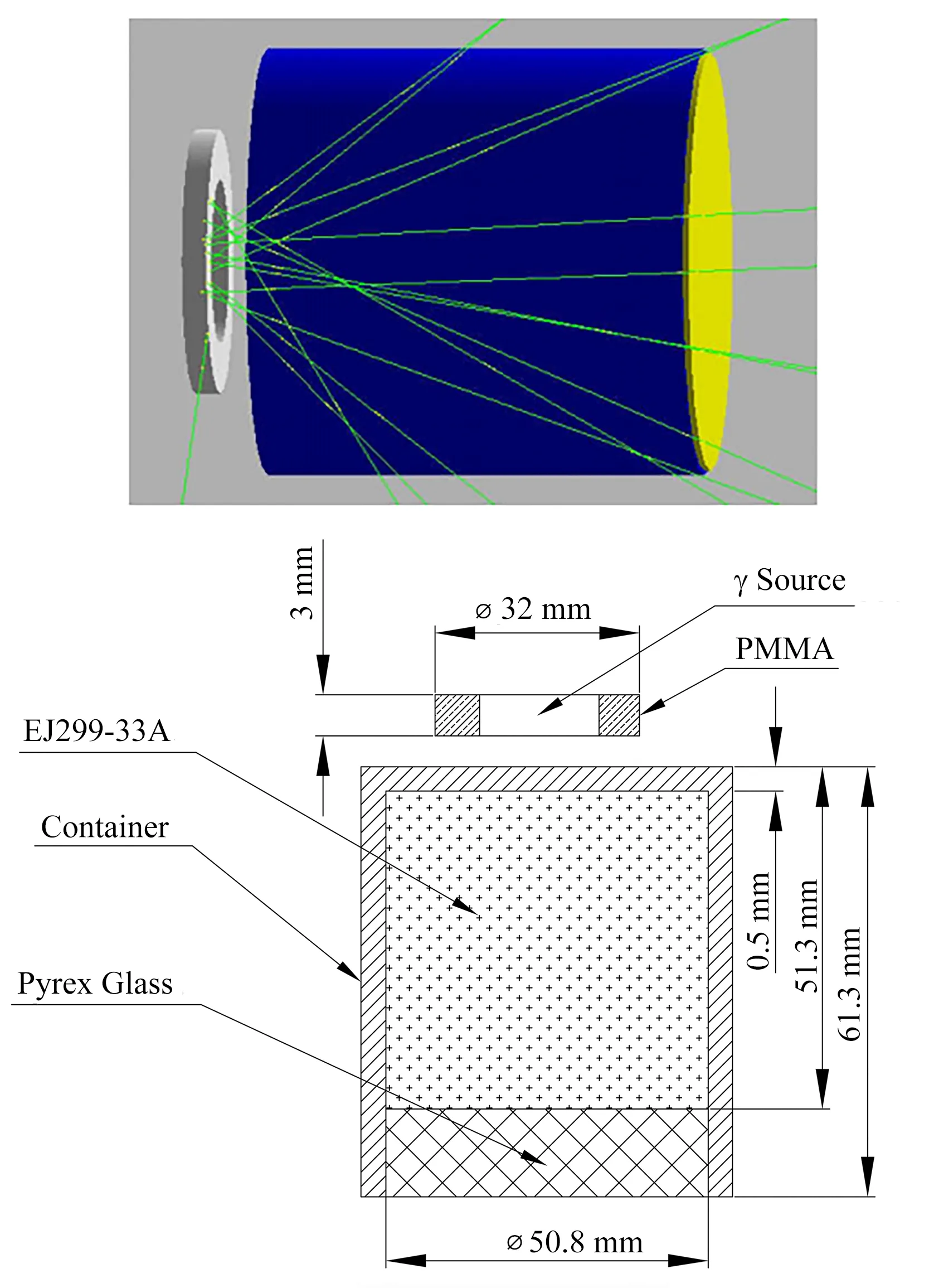
图2 EJ299-33A探测器结构和Geant4计算模型Fig.2 Structureof EJ299-33A detector and calculation model of Geant4

标准γ放射源通常是将放射性物质均匀分布在一定大小的聚酯薄膜上，再在适当的条件下通过热密封的方法制作而成的［14］。实验中使用的标准γ源是中国计量科学研究院制备的，放射性物质均匀分布在外直径为32 mm、内直径20 mm的有机玻璃环（Polymethyl Methacrylate，PMMA）内。在环内圆形区域内向外均匀发射γ射线，由于放射源与探测器之间的距离非常小，立体角设置为2π。模拟过程中考虑了探测器的结构等相关细节，闪烁体与光电倍增管（Photomultiplier Tube，PMT）之间通过1 mm厚的玻璃紧密相连接，PMT及其他导线对实验产生的影响在能量分辨函数中进一步考虑。入射γ射线与探测器相互作用产生的电子能量沉积和步长都被逐个事件记录，并通过以下公式转换成光输出［8，15］：

式中：L是闪烁光输出；a是光输出缩放参数；Ee是闪烁体中沉积的电子能量；E0是由于较低能量下的非线性关系形成的一个参数。在本实验的模拟中a=1和E0=0。

为了将模拟光输出与实验数据进行直接对比，采用高斯展宽法对分辨率为∆L的光输出L进行了能量分辨展宽。考虑由于探测器的形状、尺寸、分辨率等因素造成的光输出谱线形状的影响，其分辨率函数可以表示为［8，15−16］：

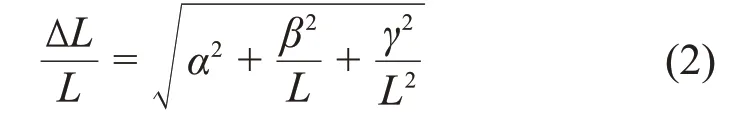
式中：α表示从闪烁体到PMT光电阴极的轨迹依赖光传输产生的影响，它限制了探测器系统在高脉冲高度的分辨率；β表示光产生、衰减、光子电子转换和电子放大的统计变化产生的影响；γ表示由PMT（暗电流）和电子系统的噪声引起的影响。任何特定探测器装置的分辨率参数必须通过单能光子和中子源的实验或理论估算来确定。标准60Co和137Cs放射源的实验光输出谱和Geant4模拟结果如图3所示，从图3中可以看出Geant4模拟很好地再现了康普顿边缘。然而，较低光输出区域模拟值比实验值低。主要原因可能来自：1）模拟中没有考虑光子与周围物质散射，如：探测器架子、实验台等；2）模拟中没有考虑闪烁体和光电倍增管边缘和壁效应。

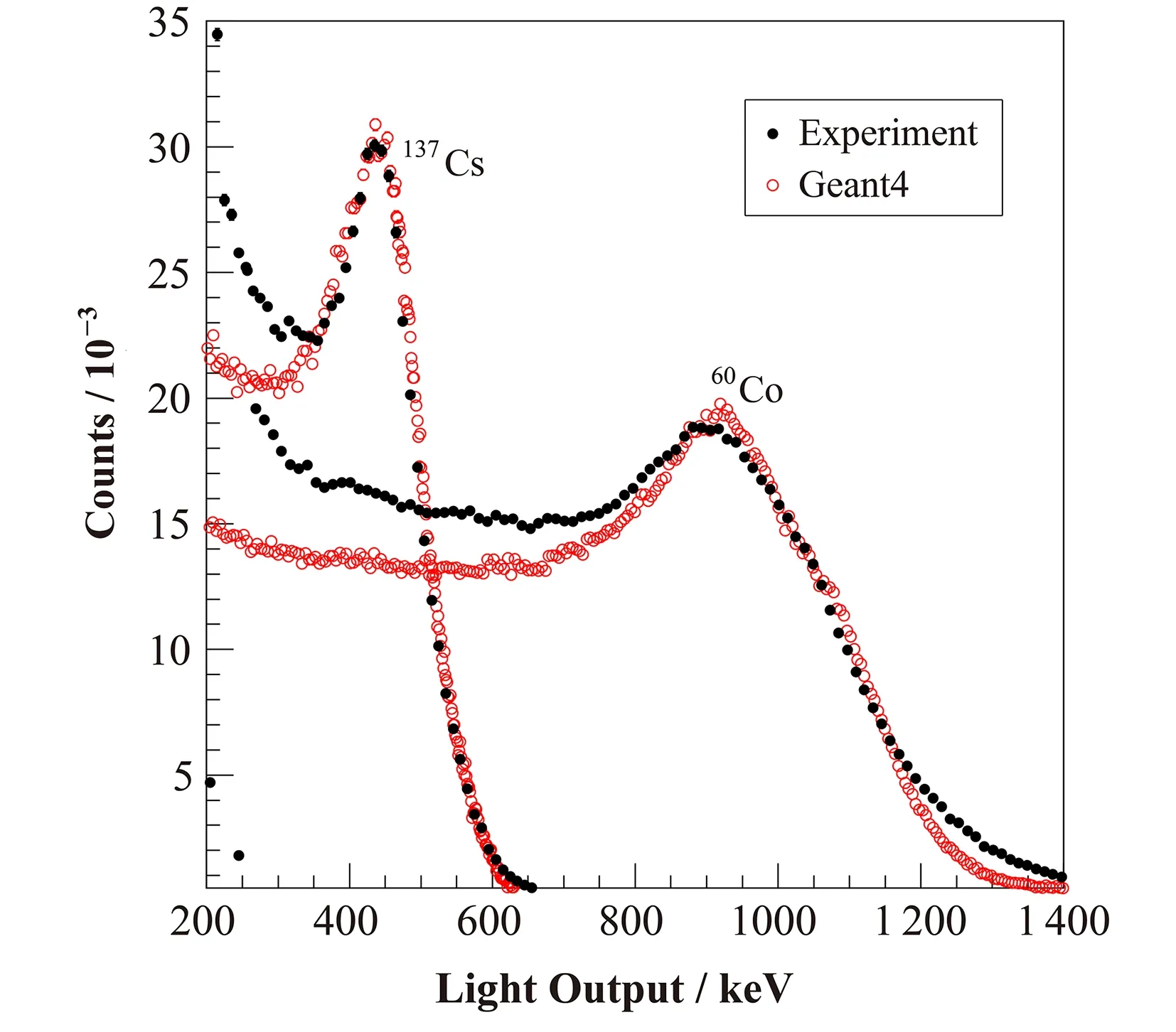
图3 实验数据与Geant4光输出对比Fig.3 Light output comparison between experimentaldata and Geant4 simulation

3 电子能量刻度

使用标准γ源对有机闪烁体探测器进行能量刻度时，必须准确地测定γ光输出谱中康普顿边缘的位置，但是由于探测器的能量分辨率会导致光输出谱具有一定的展宽，无法直接确定康普顿电子的最大能量。利用蒙特卡罗模拟探测器的γ光输出谱来确定数据获取的道数与电子能量之间的关系是较为准确和常用的方法［7−8］。康普顿反冲电子的最大能量Ec由式（3）计算：

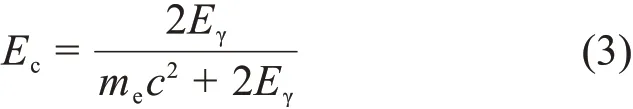
式中：Eγ为标准放射源的入射能量；mec2为电子的能量。图4中给出了137Cs源的实验测量光输出谱和Geant4模拟计算中有和无探测器能量分辨率展宽的结果对比。由此获得探测器分辨率函数参数最佳值为α=0.05、β=0.12、γ=0.002。通过比较测量的光输出分布和模拟结果对应的康普顿边缘的位置，并利用一阶多项式拟合，获得实验测量的多道道数与能量的刻度系数，从而确定探测器的电子能量刻度函数，如图5所示。能量刻度公式表示为L（Ee）=b0+b1Ee，其中：b0=0.125±0.126；b1=0.275±0.014。

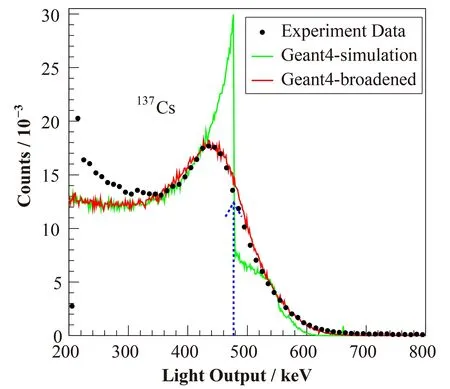
图4 实验数据和Geant4模拟结果对比Fig.4 Comparison between experimentaldataand Geant4 simulation with or without resolution broadening

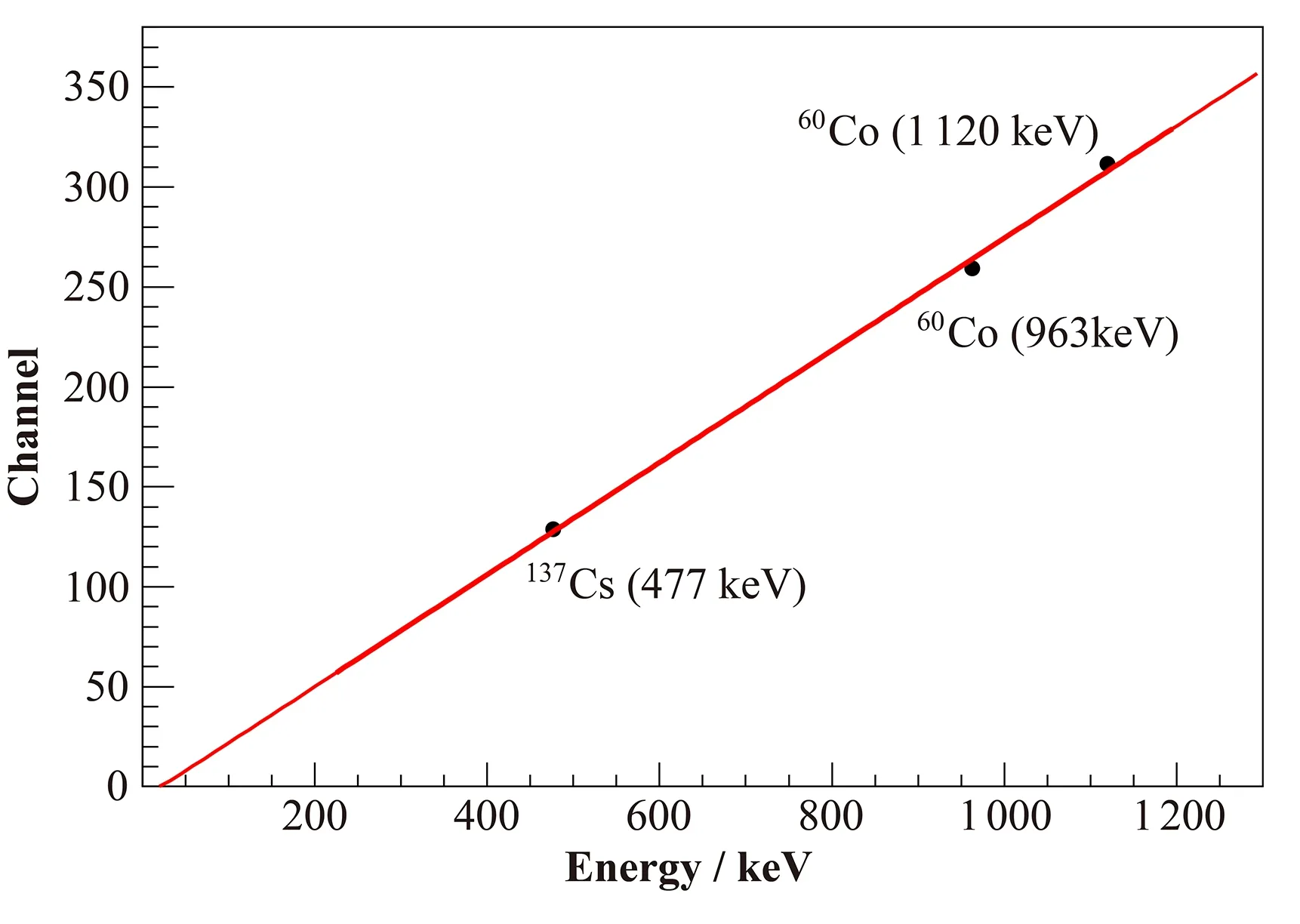
图5 探测器的能量刻度曲线Fig.5 Energy calibrationcurve of EJ299-33A detector

4 电子能量与中子探测

中子探测效率计算主要与入射中子能量、探测器的光响应函数以及中子探测阈值有关，即与闪烁体中产生的光输出刚好等于在给定的实验分辨水平下被探测到平均反冲质子能量［17］。单能中子的探测效率可以近似随（1−Eth/En）变化，其中Eth为中子探测阈值，En为中子能量，可见探测效率的误差直接取决于探测阈值的误差。当中子能量小于2Eth时，随着入射中子能量的降低，探测效率的相对误差将会迅速增大。闪烁体探测器的有效中子探测阈可以通过探测器的电子能量校准和从质子对电子的响应中取等效质子能量来获得［18］。闪烁体探测器中由于中子相互作用而产生的带电粒子的光输出可以用Birks和Cecil公式来估计［19−20］。在Cecil公式中，能量为Ep的质子的总光输出可表示如下形式：

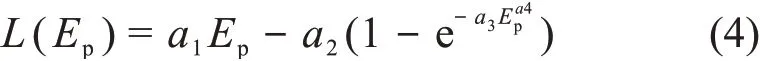
其他一些文献中也提出了多项式拟合、有理形式和幂指数形式［21］等。文献［12］中应用EJ299-33A计算得到的各参数为：a1=0.6，a2=2.2，a3=0.3，a4=1。将能量刻度公式带入式（4）中，就可得出质子响应函数和等效电子能量之间的关系：

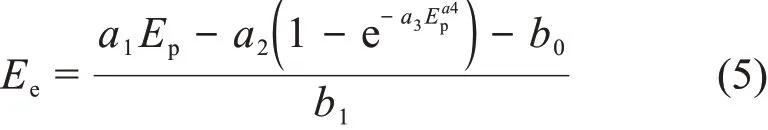
将式（5）中带入相关参数计算可知：137Cs标准γ源发出的662 keVγ射线所产生的总能量峰值约等于2.385 MeV中子（即反冲质子）产生的能量。这与文献［12］可能略有不同，主要是因为采取不同的能量刻度方法和实验装置所导致的。

5 能谱-剂量转换函数

利用γ能谱全谱法可测量放射性环境中空气吸收剂量率，进而估计环境辐射本底。全谱法的关键在于建立一个准确的能谱-剂量转换函数G（E）［9］，加权处理探测器γ能谱（即光输出谱），计算出相应的γ剂量率。

通过全谱法计算空气吸收剂量D表示为；

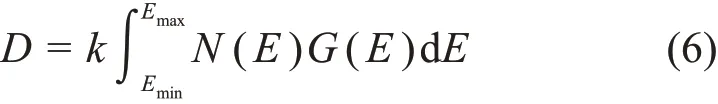
式中：k为常数；N（E）是探测器测得的γ能谱；G（E）是能谱-剂量转换权重函数；Emin和Emax为能谱积分时的阈值范围。G（E）函数有多种函数表示形式，常用对数形式进行展开：

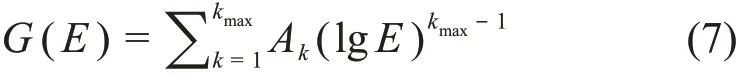
式中：kmax为G（E）函数的阶数；Ak是待定的系数，结合式（6）和（7），在已知空气吸收剂量率的情况下，通过最小二乘法就可以求解的系数Ak［9，22］。

假设多道的能宽为∆E，道数为I，入射的γ能量为Ej，将式（7）代入式（6）后，实验上利用多道计算出的空气吸收剂量D（Ej）可表示为：

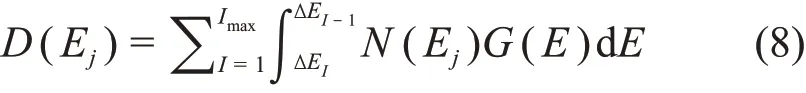
式中：Imax是最大道址［9］。模拟时标准源对应的空气吸收剂量率可表示为（未考虑自吸收）［23］：

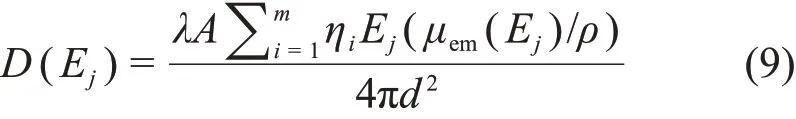
式中：λ为常数项λ=1.602 1×10−7；A为标准源的活度；ηi是能量为Ej的γ射线分支比；Ej为标准源的γ射线能量；（µem（Ej）/ρ）为相对于能量为Ej时的入射γ射线在空气中的质能吸收系数；d=d1+d2/2，d1为点源到探测器表面的距离，d2为探测器的厚度。

由于γ能谱仪的能量响应范围为100 keV∼3 MeV，环境辐射能量一般在3 MeV以下［24‒25］，因此模拟谱选取的入射粒子能量分别为：从200 keV∼3 MeV区间，每隔200 keV选取一个能量点，一共选取15个能量点。模拟了对应能量的光输出分布谱，利用其作为标准谱求解G（E）函数。

利用最小二乘法求解Ak系数时，不同的kmax对计算的结果影响也是很大，表2计算kmax=6∼10对应的平均相对误差，最终选取kmax=10，相应的系数分别为：A1=−1.472×10−9、A2=7.699×10−7、A3=−1.598×10−6、A4=1.270×10−6、A5=−4.051×10−7、A6=−3.348×10−8、A7=6.754×10−8、A8=−2.176×10−8、A9=3.136×10−9、A10=−1.774×10−10。表3为不同的γ射线能量对应的G（E）函数计算值、理论值及偏差的计算结果。从表3中可知不同能量的偏差均在0.53%以内，相对偏差S=|Sj|/n为0.249。在计算过程中模拟谱和实验谱积分下阈值均设置为100 keV，上阈值均为3 MeV。

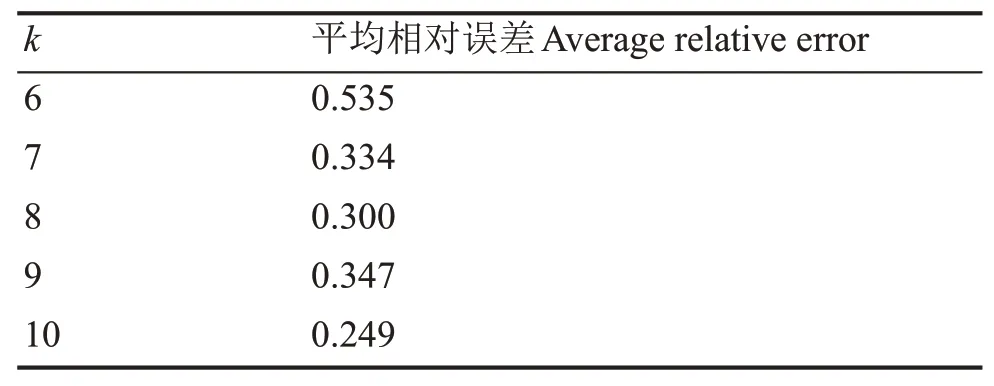
表2 不同k值对应的平均相对误差Table 2 Average relative error corresponding to different k values

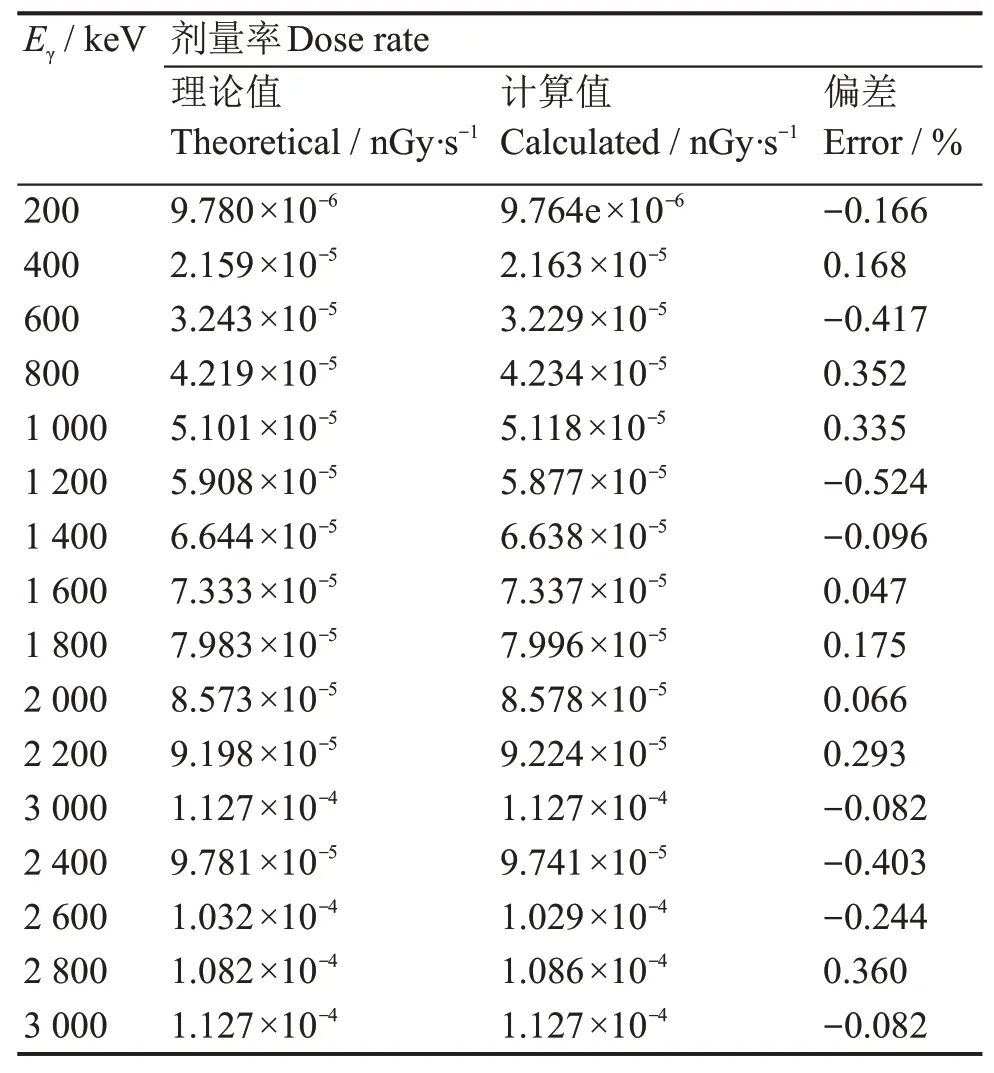
表3 不同γ射线能量的G(E)函数剂量率计算值、理论值及偏差Table 3 Calculation value,theoretical value and deviationof G(E)function with differentγ-ray energy

6 结语

本文采用标准放射源137Cs和60Co实验测量了EJ299-33A塑料闪烁体光输出谱，并利用Geant4蒙特卡罗程序计算了不同γ射线对探测器的光输出谱。Geant4模型中详细考虑了探测器尺寸、材料成分和能量分辨率。通过对比实验测量光输出谱与Geant4计算结果，准确确定了γ射线在探测器的康普顿最大电子能量位置，使用最小二乘法拟合获得了探测器电子能量刻度函数。基于Cecil公式对EJ299-33A塑料闪烁体质子响应函数的描述，利用探测器电子能量刻度函数与中子产生的反冲质子关联，深入研究了中子探测器阈值对电子能量刻度的依赖关系。同时，Geant4模拟计算了200 keV∼3 MeV区间的15个不同能量点的EJ299-33A探测器γ光输出谱，利用全谱法结合空气吸收剂量理论值获得了能谱-剂量转换函数G（E），不同能量的偏差均在0.53%以内。

作者贡献声明王德鑫负责文章的起草和最终版本的修订；张苏雅拉吐负责论文的修改；胡新荣负责理论模型的分析；任杰负责实验数据分析的讨论；红兰负责资料的搜集和整理；王金成负责资料的搜集和整理；宋娜负责资料的搜集和整理；王宏伟负责研究的提出及设计；黄美容负责研究的提出及设计；唐鑫负责资料的搜集和整理；立立负责资料的搜集和整理；白嘎拉负责资料的搜集和整理；牛丹丹负责资料的搜集和整理。