求解最小支配集的线性混合整型规划算法

程咏锋，吴歆韵，熊才权

(湖北工业大学计算机学院，湖北 武汉 430068)

最小支配集问题为NP难问题，是一类重要的组合优化问题。对于最小支配集问题的求解不可能出现多项时间精确算法。最小支配集问题及其各种拓展问题在多文档摘要[1]，社会网络的建模和研究[2]，通信网络[3]等诸多领域具有广泛的应用。

目前，求解最小支配集问题精确算法均为非多项式时间算法，Fomin F V[4]等提出一种分支简化(FKW)算法，尽管最早突破O(2n)界限,但FKW仍难令人满意,如果图中没有低于2度的节点,算法将回归平凡的枚举。Grandoni F[5]等人提出了求最小支配集的Grandoni算法，但该算法只能求最小支配集的大小，不能求具体的最小支配集；Lu gang[6]等对该算法提出了修改，应用于求解具体的最小支配集；Headar[7]等提出一种混合遗传算法，与局部搜索算法相结合，设计出特定的适应度函数求解最小支配集，该算法在文献[8]中得到改进。David[9]等针对大型图的最小支配集问题，提出一种新的基于顺序的随机局部搜索算法。Zhu X[10]提出求解最小支配集的多项式时间近似方案，但这些算法不能在一般图上得到应用。Yuan Fuyu[11]通过分析大规模实例，结合支配集问题的特点提出一个快速高效地求解最小支配集问题的算法(Fast MDS)，其他最小连通支配集算法参见文献[12-14]。

本文根据最小支配集问题的性质，构造出一种求解该问题的数学模型，采用java语言实现邻接支配矩阵的存储和根据数学模型利用Gurobi优化器进行线性求解，并与文献[6]提及到的FKW算法，Grandoni算法和改进的Grandoni算法在当前国际文献公开的共74个算例上进行比较，该算法的计算效率明显优于其它的精确算法，并且在所有算例上都能得到较好的精确解。

1 最小支配集问题的描述

1.1 问题定义

对于无向不连通图G=(V,E)，图G的顶点集合为V=V(G)，图G的边集合为E=E(G)。若顶点集合V当中存在一个子集D⊆V,对于集合V当中的任意一个顶点Vp，要么Vp∈D，要么Vp与集合D当中某个顶点相邻，则将集合D称为图G=(V,E)的一个支配集。当集合D当中任意一个真子集都为非支配集时，则称集合D为图G的一个极小支配集。

设集合D是图G=(V,E)的一个支配集，当图G当中不存在任何一个支配集D1，使得|D1|<|D|，此时的集合D称为图G=(V,E)的一个最小支配集，图G当中所有最小支配集的大小称为图G=(V,E)的支配数，表示为γ(G)。

以下给出最小支配集问题的相关定义:

定义1 支配集(Dominating Set)：集合D⊆V(G)，若任意的Vp∈V(G)-D，存在一个顶点Vq∈D，使得顶点Vp与顶点Vq之间有边相连，满足这样条件的集合D就构成了图G的一个支配集,简记为DS。

定义2 极小值支配集(Minimal DS)：设集合D为图G=(V,E)的一个支配集，当集合D当中的任意一个真子集都无法构成图G=(V,E)的一个支配集，则称集合D为图G=(V,E)的一个极小支配集。

定义3 最小支配集(Minimum DS)：在图G=(V,E)的所有支配集当中，顶点个数最少的那个支配集称为图G=(V,E)的最小支配集。简称MDS。

由相关支配集的定义可知极小支配集和最小支配集的相关性质：

1)对于一个任意的非空图G=(V,E),可以找到若干个极小支配集，这些极小支配集的阶(顶点数)不一定相同。

2)对于一个任意的非空图G=(V,E)，可以找到若干个最小支配集，这些最小支配集的阶(顶点数)一定相同。

3)如果一个集合X，满足最小支配集的条件，那么集合X一定满足极小支配集的条件；反之，若集合X满足极小支配集的条件，那么集合X未必满足最小支配集的条件。

1.2 整数规划模型

最小支配集问题指的是对于给定的图G=(V,E)，在集合V中找到一个支配集D,使得支配集D中所含节点的个数达到最小。通过引入n维0-1向量X=(x1，x2，x3，…，xn)，xp=1表示顶点p∈D，xp=0表示顶点p∉D，则最小支配集的整数规划模型可以描述为式(1)-(4)：

(1)

s.t.

(2)

(3)

(4)

四个公式分别表示为：1)f(X)作为目标函数表示以最少的顶点集合作为支配点，2)为约束条件表示任意一个顶点Vp要么是支配点，要么被支配集和当中的点所支配，n表示图顶点的个数。3)LP,q为常量，表示第p节点是否可以与第q节点互相支配，是则为1，否则为0。4)变量xp表示是否选取第p个节点作为最小支配集，是则为1，否则为0。

2 图的最小支配集的多项式方程组模型与Gurobi求解器求解

Gurobi是由美国Gurobi公司开发的新一代大规模优化器，综合能力强，性价比较优。它支持Windows,Linux,MacOSX等多种平台,采用了 最新的优化技术,充分利用多核处理器优势,支持并行计算;问题尺度只受限制于计算机内存容量,不对变量数量和约束数量有限制;提供了方便轻巧的Java接口;能够快速高效地解决大规模线性问题、二次型目标问题、混合整数线性和二次型问题等数学问题。

设图G=(V,E)是无向图，则图G的邻接矩阵定义为A=[vpq]n×n，其中

(1)

通常将A的第i行记为Ai，1≤i≤n。此外在此基础上定义邻接支配矩阵

A*=[vpq]n×n

其中

(2)

对于给定具有n个顶点的无向图G=(V,E)，其邻接支配矩阵为A*=[vpq]n×n。由最小支配集的定义可知，求解一个多元多项式方程组的0-1解与求解图G的最小支配集这两个问题是等价的，即n维向量X中所含1的个数达到最小。

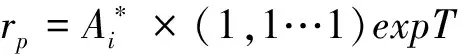
(3)

设n维向量Xk=(x1，x2，x3…xn)expT,若该n维向量满足(Ck)的所有不等式，故向量Xk是方程组(Ck)的一个解。则其中取值为1的变量所对应的顶点构成的集合为支配点集合，取值为0的变量所对应的顶点构成的集合为被支配点集合。

通过Java语言实现无向图的支配矩阵存储，设置最优化模型的系数列表，调用Gurobi优化器进行优化求解。首先使用grbModel.addVar函数构建目标函数系数列表；其次使用grbModel.addConst构建约束条件的系数列表；最后使用grbModel.setObjective函数优化求解。利用公共线性规划求解器对其进行求解, 使得目标函数值不断减小，最终可求得一个最小的k值。

3 实验结果与分析

本节主要是对求解最小支配集的MILP算法的性能进行实验分析。并与文献[6]提及到的FKW算法和Grandoni算法以及改进的Grandoni算法在当前国际文献公开的共74组算例上进行比较。第一组算例为文献中作者[15]随机生成的大规模算例。第二组算例，包含广泛的真实图，研究于许多领域，特别是在图染色问题上[16]。

实验环境:本次实验所涉及的算法均以Java语言进行编程实现, 测试运行的 PC 机运行环境为 Core i5 3.4 GHz CPU 和 8.0 GB RAM, 操作系统为 Windows 10,JVM 为 Oracle JRE 1.8。为了验证算法的性能,采用两组算例进行实验验证。

3.1 随机算例的测试

第一组算例为随机生成的24组小规模算例，算例生成方法为：在一个N×N的固定区域中随机选取一定数量的节点作为算例的图节点；当区域内的两节点p，q之间的距离小于某个设定的常数k值时，将{p，q}作为算例图中的一条边，即两节点p，q之间相互连通。该组随机算例节点数从20-120，每组算例运行10次，求出最优解的时间并取平均值，结果见表1。表1前两列分别表示算例的名称和最小支配集个数，其余列表示每个算法运行10次找到最小支配集个数时所需要的平均时间。

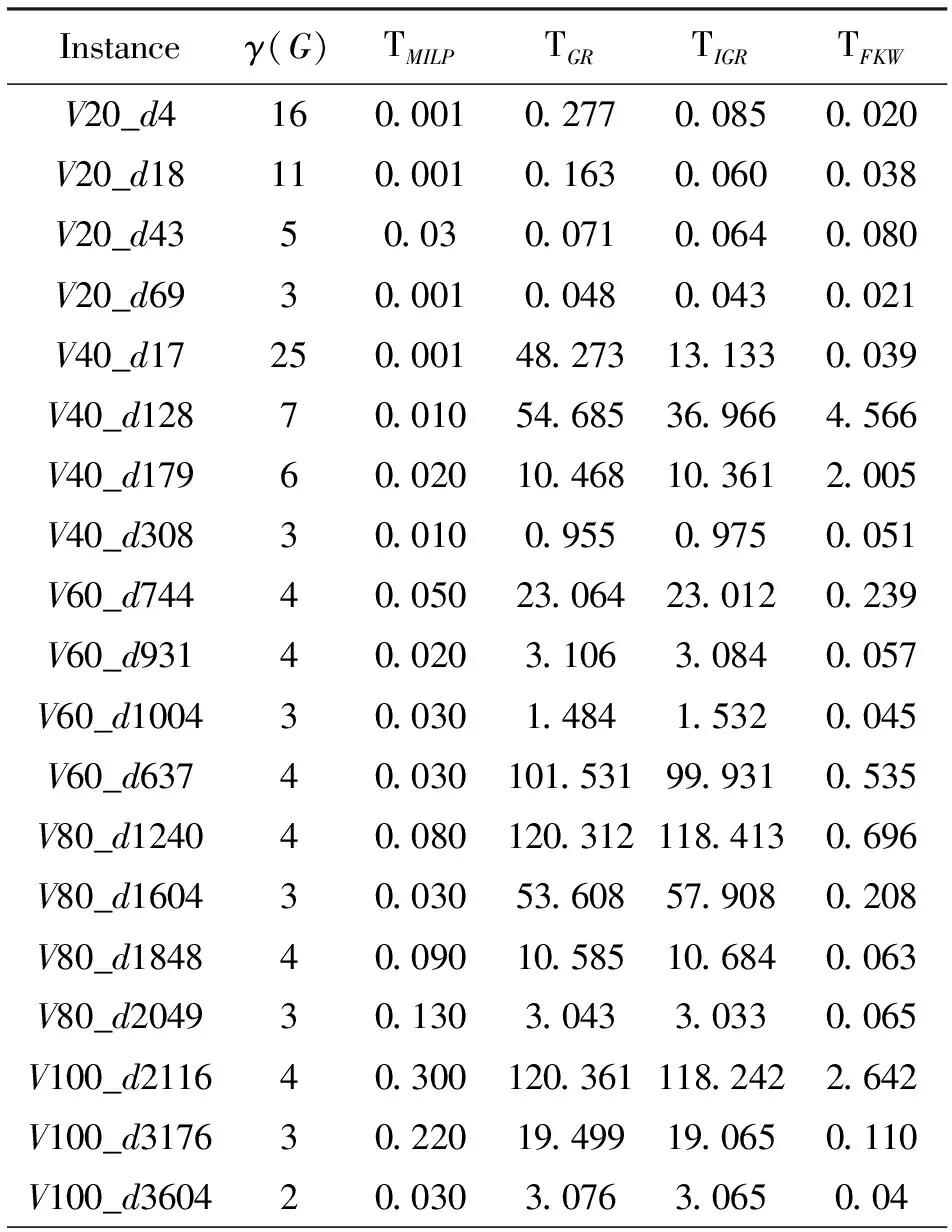
表1 随机算例对比 s

图1为表1的信息汇总。通过图1，可以明显看到，求出24组小规模算例的最小支配集，FKW算法用了16.239 s，Grandoni算法用了1257.115 s，改进的Grandoni算法用了1217.891 s，而提出的MILP算法给出了2.674 s的最好结果，根据在随机生成的24组小规模算例上的结果，MILP算法具有更好的性能。

图 1 精确算法的总耗时

3.2 图着色算例测试

由于第一组图的最小支配集较小，实验结果具有局限性。因此对第二组图进行测试，这个测试涉及到宽面图，该50组算例顶点规模从11到864个顶点不等，这些算例已经在许多研究中使用，特别是在图着色的问题上。这次测试包含50组算例，每组算例运行10次，测试结果见表2。

在图着色算例上的测试结果见表2，前四列分别表示算例的名称，顶点个数，边数，最小支配集个数，后四列分别表示FKW算法，GR算法，IGR算法，以及MILP算法求出最优解所需花费的时间。“-”表示未能给出最优解，“>3600”表示程序运行时间超过一小时，表3是表2的汇总，显示了各算法在1小时内成功求出最优解算例的个数。

从表2的结果可以看出，对于复杂算例的计算，IGR算法的性能要优于GR算法，FKW算法在计算时会造成程序崩溃。在除Le450-5c外的所有算例上，MILP算法对于其余49个算例均能在一小时内找到最优解。通过表3的汇总可以看出，对比其他三个算法，MILP算法在一小时的计算时间内成功率达到98%，在所有算例上MILP算法的求解速度均快于其他算法，并且对于比较复杂的算例，MILP算法求解的速度更快，这些数据表明，MILP算法是求解最小支配集问题的一种高效的精确算法。

表2 图着色算例对比

表3 图着色算例结果汇总

4 结论

本文提出了一种求解最小支配集问题的线性混合整数规划算法,在MILP算法中，根据最小支配集问题的特点，提出一种新的整数规划模型，将该问题转化为线性规划问题，运用Gurobi求解器进行线性求解。采用当前国际文献公开的共74组算例作为算法测试实验集，在与文献中介绍的其他精确算法进行比较后发现，MILP算法在中小规模的算例上能够以较快的时间求出最优解，对于较为复杂的算例，MILP算法都能求出最优解，并且在计算出最优解的时间上具有明显优势。