平面向量常见典型考题赏析
■张文伟

平面向量是高中数学的重要概念,是沟通代数、几何与三角函数的一种工具,并且是有效解决几何问题的一种有力工具。向量概念引入后,全等和平行、相似、垂直、共线、轨迹等就可以转换成向量的加减法、数乘向量、数量积运算,从而将图形的基本性转化为向量的运算体系。平面向量作为数学知识网络的一个交汇点,它是联系众多知识的媒介与桥梁,因此以向量为工具成为高考命题的一个亮点。下面就平面向量常见的典型考题举例分析,供大家学习与参考。
题型1:向量的有关概念
零向量和单位向量的两个注意点:零向量的方向是任意的,所有的零向量都相等;单位向量的方向不定,所有的单位向量不一定相等。共线向量与平行向量的区别与联系:平行向量也称为共线向量,共线向量所在的直线可以平行,与平面几何中的共线不同;平行向量可以共线,与平面几何中的直线平行不同。解决与向量概念有关问题的关键是突出向量的核心——方向和长度。
例1下列说法正确的是( )。
A.数量可以比较大小,向量也可以比较大小
B.方向不同的向量不能比较大小,但同向的可以比较大小
C.向量的大小与方向有关
D.向量的模可以比较大小
解:不管向量的方向如何,它们都不能比较大小,A 不正确。方向相同的向量也不能比较大小,B 不正确。向量的大小即向量的模,指的是有向线段的长度,与方向无关,C不正确。向量的模是一个数量,可以比较大小,D 正确。应选D。
跟踪训练1:给出下列四个命题:①若向量a=,则|a|=|b|;②若a是单位向量,b也是单位向量,则a与b的方向相同或相反;③若向量是单位向量,则也是单位向量;④以坐标平面上的定点A为起点,所有单位向量的终点P的集合是以A为圆心的单位圆。
其中正确命题的序号____是 。

题型2:向量的表示及应用
向量的两种表示方法:(1)几何表示法,先确定向量的起点,再确定向量的方向,最后根据向量的长度确定向量的终点;(2)字母表示法,为了便于运算可用字母a,b,c表示,为了联系平面几何中的图形性质,可用有向线段的起点与终点表示向量,如等。用几何表示法表示向量,便于用几何方法研究向量运算,为用向量处理几何问题打下了基础;用字母表示法表示向量,便于向量的运算。
例2某人从A点出发向东走了5m 到达B点,然后改变方向按东北方向走了m到达C点,到达C点后又改变方向向西走了10m 到达D点。

解:(1)由题意作出向量,如图1所示。
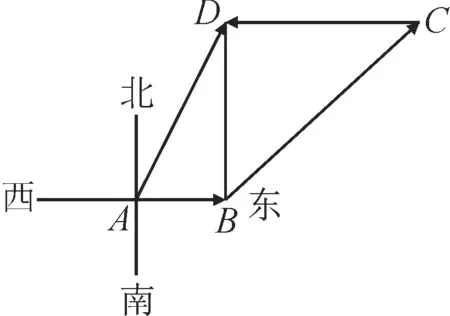
图1
(2)由题意知,∠DBC=∠DCB=45°,所以△BCD是等腰直角三角形,其中∠BDC=90°,BC=(m),CD=10(m),所 以BD=10(m)。△ABD是直角三角形,其中∠ABD=90°,AB=5(m),BD=10(m),所以AD=),所以)。
跟踪训练2:某次军事演习中,红方一支装甲分队为完成对蓝军的穿插包围,先从A处出发向西迂回了100km 到达B地,然后又改变方向向北偏西40°走了200km 到达C地,最后又改变方向,向东突进100km 到达D处,完成了对蓝军的包围。
提示:(1)由题意作出向量,如图2所示。

图2

题型3:相等向量和共线向量
相等向量与共线向量的探求方法:(1)寻找相等向量时,先找与表示已知向量的有向线段长度相等的向量,再确定哪些同向共线;(2)寻找共线向量时,先找与表示已知向量的有向线段平行或共线的线段,再构造同向与反向的向量,注意不要漏掉以表示已知向量的有向线段的终点为起点,起点为终点的向量。需要注意的是,在求解与向量平行相关的问题中,不要忽视零向量。
例3若四边形ABCD是矩形,则下列说法不正确的是( )。

跟踪训练3:设a,b是两个平面向量,则“a=b”是“|a|=|b|”的( )。
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
提示:若a=b,则|a|=|b|,而|a|=|b|不能推出a=b,所以“a=b”是“|a|=|b|”的充分不必要条件。应选A。
题型4:向量的加减法运算

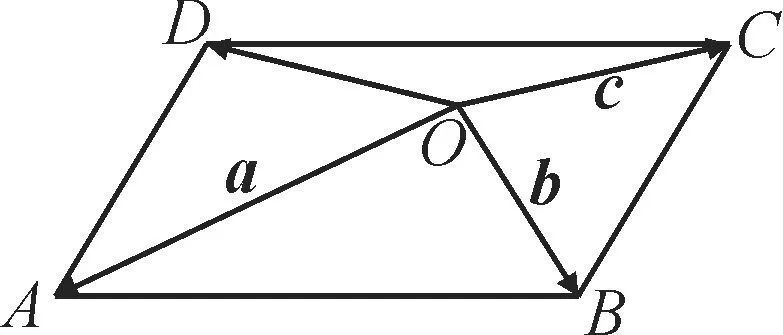
图3

题型5:向量的数乘运算
证明或判断三点共线的两种方法:一般来说,判断A,B,C三点共线,只需存在实数λ,使得即可;若存在实数x,y,使得且x+y=1,则A,B,C三点共线。证明向量共线,可根据向量共线定理,寻求唯一实数λ,使得b=λa(a≠0)。已知向量共线求参数的值,可根据向量共线的条件转化为相应向量的系数相等求解。若两个向量不共线,必有向量的系数为零,利用待定系数法建立方程求得参数的值。
例5已知两个非零向量a与b不共线。
(2)试确定实数k,使得ka+b与a+kb共线。

(2)由两个向量共线,列出关于a,b的等式,再由a与b不共线求解。
由ka+b与a+kb共线,可知存在实数λ,使得ka+b=λ(a+kb),即ka+b=λa+λkb,所以(k-λ)a=(λk-1)b。因为a,b是不共线的两个非零向量,所以k-λ=λk-1=0,可得k2-1=0,解得k=±1。
跟踪训练5:设a,b是两个不共线的向量。若向量ka+2b与8a+kb的方向相反,则k=____。
提示:因为向量ka+2b与8a+kb的方向相反,所以ka+2b=λ(8a+kb)。由向量相等可得解得k=-4(两个向量的方向相反时λ<0,也即k<0)。
题型6:向量的数量积
求两个向量的数量积,首先确定两个向量的模及两个向量的夹角,其中准确求出两个向量的夹角是求数量积的关键。求向量的模,一般转化为求模的平方,且与向量的数量积联系,灵活运用公式a2=|a|2,最后勿忘开方。利用a·a=a2=|a|2或|a|=,可以实现实数运算与向量运算的相互转化。
例6如图4,在△ABC中,D是BC的中 点,E,F是AD上的两个三等分点,=-1,则的值是______。
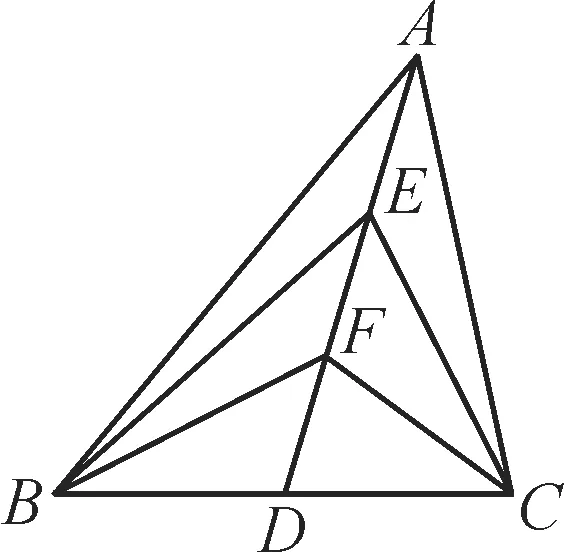
图4


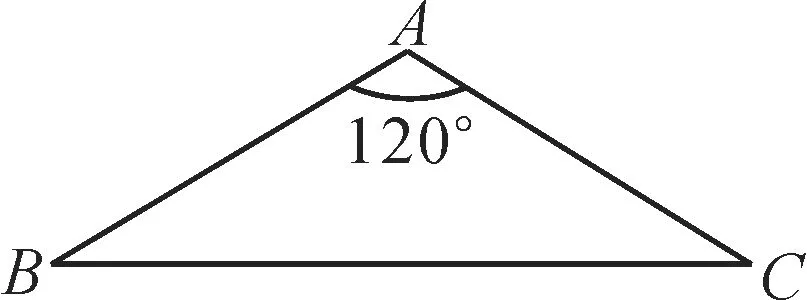
图5

题型7:平面向量基本定理
如果e1和e2是同一平面内的两个不共线向量,那么对这一平面内的任一向量a,有且只有一对实数λ1,λ2,使得a=λ1e1+λ2e2。同一平面内的两个不共线向量都可以作为基底,基底不唯一;同一非零向量在不同基底下的分解式是不同的;基底给定时,分解形式唯一。e1,e2是同一平面内所有向量的一组基底,当a与e1共线时,λ2=0;当a与e2共线时,λ1=0;当a=0时,λ1=λ2=0。由于零向量与任何向量都是共线的,因此零向量不能作为基底向量。

跟踪训练7:已知{a,b}是一个基底,实数x,y满足(3x-4y)a+(2x-3y)b=6a+3b,则x-y的值为____。
提示:因为{a,b}是一个基底,所以a与b不共线。又因为(3x-4y)a+(2x-3y)b=6a+3b,所以解得x=6,y=3,所以x-y=3。
题型8:平面向量的正交分解及坐标表示
平面向量的正交分解的实质上是平面向量基本定理的一种应用形式,只是两个基底向量e1和e2互相垂直。由向量坐标的定义可知,两个向量相等的充要条件是它们的横、纵坐标对应相等,即a=b⇔x1=x2且y1=y2,其中a=(x1,y1),b=(x2,y2)。向量的坐标只与起点、终点的相对位置有关,而与它们的具体位置无关。当向量确定以后,向量的坐标就唯一确定了,因此向量在平移前后,其坐标不变。
例8已知点O是△ABC内一点,∠AOB=150°,∠BOC=90°,设=a,=c,且|a|=2,|b|=1,|c|=3,求向量的坐标。(以O为坐标原点,所在直线为x轴建立平面直角坐标系)
解:建立如图6所示的平面直角坐标系。
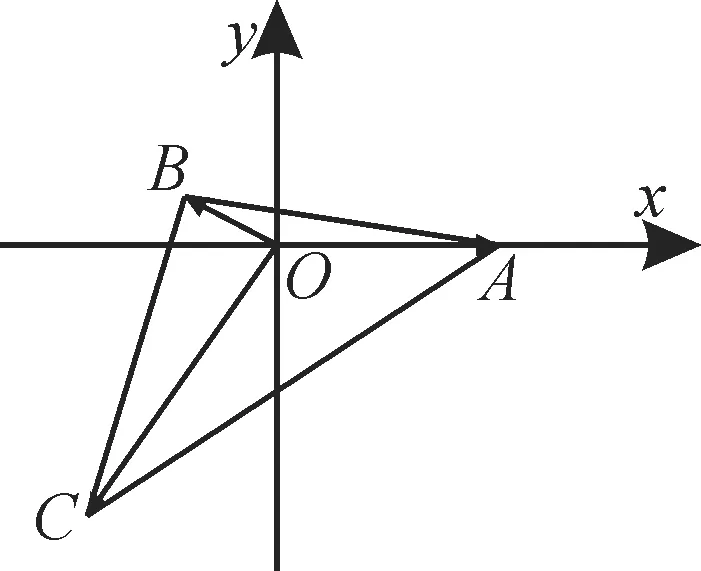
图6


题型9:平面向量数乘运算的坐标表示
两个向量a=(x1,y1)与b=(x2,y2)共线的三种表示方法:当b≠0时,a=λb,这是几何运算,体现了向量a与b的长度及方向之间的关系;x1y2-x2y1=0,这是代数运算,用它解决向量共线问题的优点在于不需要引入参数,从而减少未知数的个数;当x2y2≠0时,,即两向量的相应坐标成比例。
例9设向量a=(2,x),b=(-4,5),若a与b的夹角为钝角,求x的取值范围。

题型10:平面几何中的向量方法
用向量方法解决平面几何问题的“三部曲”:(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;(2)通过向量运算,研究几何元素的关系;(3)把运算结果“翻译”成几何关系。这三部曲给出了利用向量的代数运算研究几何问题的基本思想。在解决平面几何问题时,将平面问题转化为向量问题是关键。
例10已知A,B,C,D四点的坐标分别为(1,0),(4,3),(2,4),(0,2),则此四边形为( )。
A.梯形 B.菱形
C.矩形 D.正方形

题型11:向量在物理学中的应用
数学是物理解题过程中不可缺少的工具,向量是物理问题简化的有力法宝。用向量方法解决物理问题的“三部曲”:(1)把物理问题中的相关量用向量表示;(2)转化为向量问题中的模型,通过向量的运算使问题得以解决;(3)把结果还原为物理问题。
例11已知两个力F1,F2的夹角为90°,它们的合力大小为10N,合力与F1的夹角为60°,那么F1的大小为( )。
A.5N B.5N C.10N D.5N
解:由题意画出图形,如图7所示。
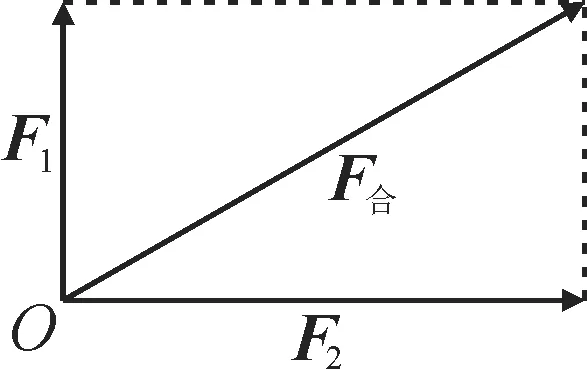
图7
由题意得|F1+F2|=|F合|=10,所以|F1|=|F合|cos60°=5(N)。应选B。
跟踪训练11:某人在静水中游泳时,速度为4km/h。如果水流的速度为4km/h,他沿着垂直于对岸的方向前进,那么他实际前进的方向与河岸的夹角为( )。
A.90° B.30° C.45° D.60°
提示:由题意画出图形,如图8所示。
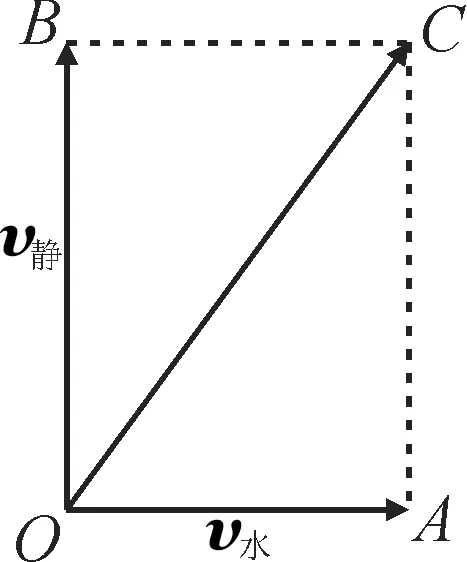
图8

题型12:余弦定理、正弦定理的应用
利用余弦定理和正弦定理可以解决求值问题,测量距离问题、高度问题、角度问题、面积问题等。
例12在△ABC中,角A,B,C的对边分别为a,b,c,已知sin2A+sin2C=sin2B+sinAsinC,若△ABC的面积为,则B=_____,当a+c的值最小时,△ABC的周长为_____。

跟踪训练12:如图9,在海岸A处发现北偏东45°方向,距A处(-1)km 的B处有一艘走私船。在A处北偏西75°方向,距A处2 km 的C处的我方缉私船奉命以10km/h的速度追截走私船,此时走私船正以10km/h的速度,从B处向北偏东30°方向逃窜。问:缉私船沿什么方向行驶才能最快截获走私船?求出所需时间。
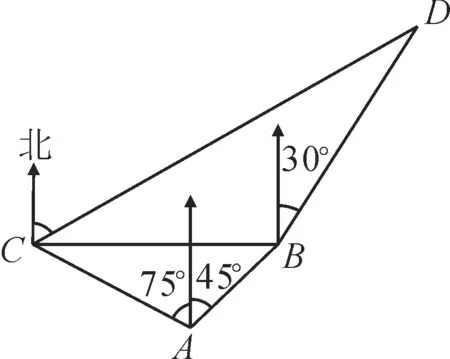
图9
提示:设缉私船应沿CD方向行驶th,才能最快截获(在D点)走私船,则CD=,BD=10t。


