浅议与平面向量最值问题有关的几种题型

■陈泽刚 杜海洋

平面向量中的最值问题是一种典型的能力考查题，它能有效地考查同学们分析问题和解决问题的能力，体现了高考在知识交汇处命题的思想。下面就平面向量最值问题有关的几种题型举例分析。

题型1：与数量积有关的最值问题

例1如图1，扇形OAB的半径为1，圆心角为，P是上的动点，则的最小值为_____。

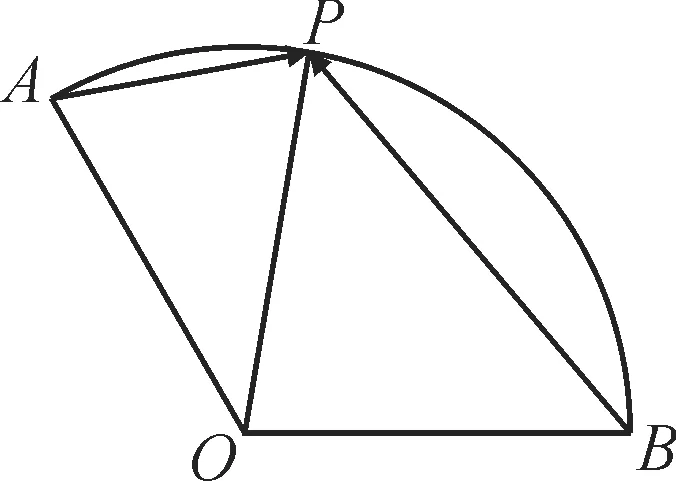
图1

题型2：与模长有关的最值问题

题型3：与三角形有关的最值问题

题型4：与二次函数有关的最值问题

例4在△ABC中，AC＝1，BC＝2，∠ACB＝60°，点P是线段BC上一动点，则的最小值是____。

分析：建立直角坐标系，根据题意求得各点坐标，利用向量的坐标运算求得数量积，再结合二次函数求出最小值。

解：在△ABC中，由余弦定理得AB＝。由此可知△ABC是直角三角形。

以点A为坐标原点，AB所在直线为x轴，AC所在直线为y轴，建立平面直角坐标系xAy，如图2所示。

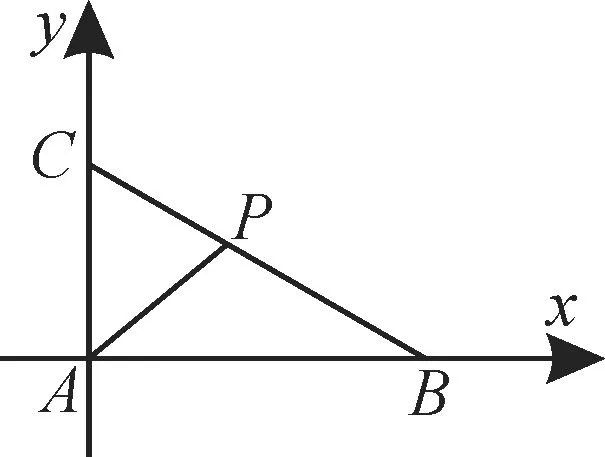
图2

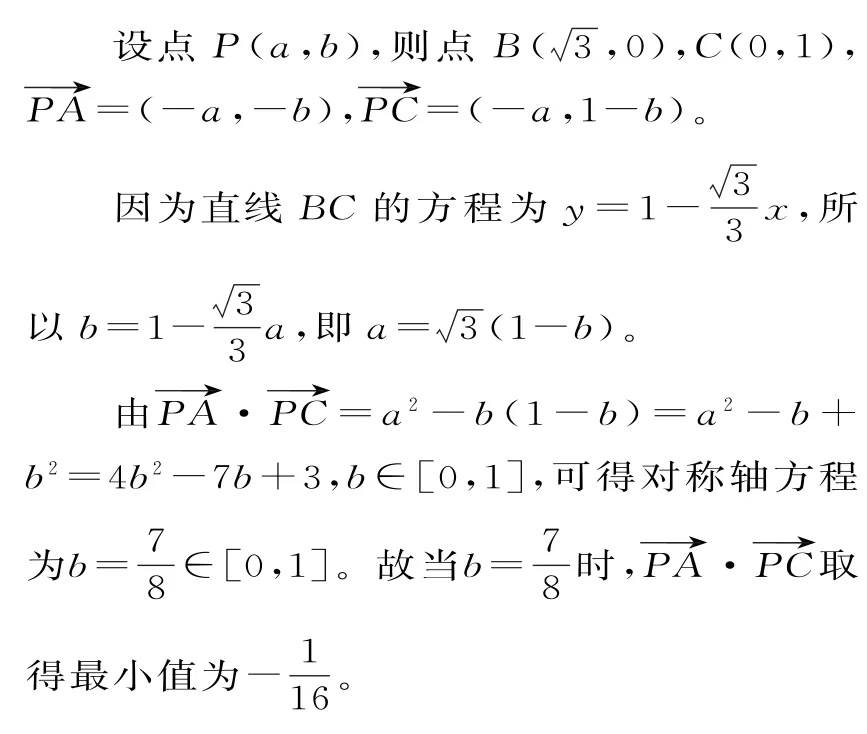
题型5：与基本不等式有关的最值问题

题型6：与三角函数有关的最值问题

小结：平面向量中的最值问题的求解通常有两种思路:一是“形化”，即利用平面向量的几何意义，将问题转化为平面几何中的最值问题，然后根据平面图形的特征直接进行判断；二是“数化”，即利用平面向量的坐标运算，将问题转化为代数中的函数最值问题。