座圈晃动对火炮高低机仿真结果的影响研究

单春来，梁辉，宁变芳，雷建平

(西北机电工程研究所, 陕西 咸阳 712099)

火炮高低机是用来驱动火炮起落部分进而赋予炮身俯仰角的传动装置，而火炮平衡机是用来平衡火炮起落部分相对于耳轴的重力矩从而保证炮身俯仰动作平稳、动力传动轻便的装置[1-2]。不同类型的火炮根据其使用条件和需求，配备不同类型的高低机和平衡机，如常见的大口径加榴炮普遍采用齿弧型高低机和气液式平衡机。现某型大口径火炮为便于实现炮塔的无人化及模块化，使用了液压式高低机和平衡机的设计方案。在样机进行射击试验的过程中，起落部分在翻倒力矩的作用下存在大幅度俯仰振动，高低机和平衡机的伸缩幅度较大且衰减时间较长，不利于自动供输弹机构装填弹药[3]，影响发射速度，需要对其原因进行分析并加以改进。通过对测试数据和高速摄影图像进行初步分析,认为该问题可能与高低机和平衡机的自身性能、炮塔刚度、座圈刚度及其间隙等影响因素有关。笔者针对这一问题开展动力学计算研究，对以上各因素进行计算和仿真分析，进而对该火炮的研制提供动力学方面的理论支撑，为后期方案的改进提供参考。

1 计算模型

火炮的几何模型及其动力学模型拓扑结构图如图1所示[4]，以RecurDyn仿真平台为工具，根据该拓扑关系图建立动力学仿真模型并进行计算[5]。

该火炮的高低机和平衡机结构示意图如图2所示。

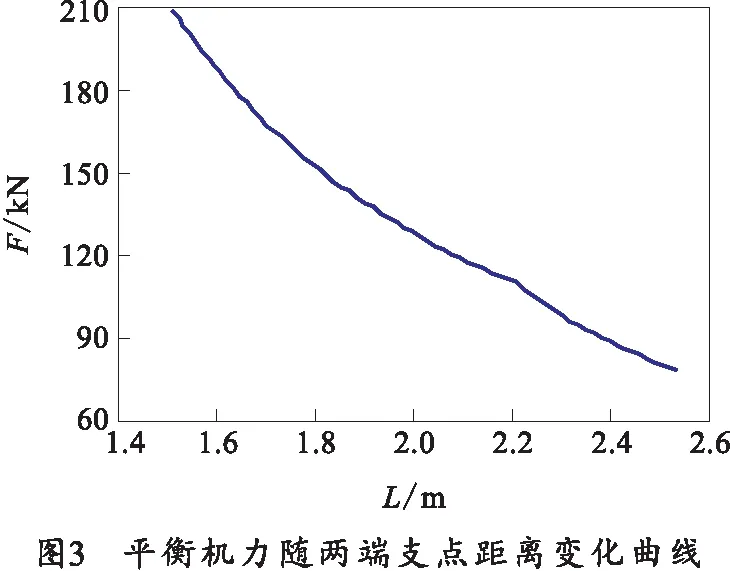
该高低机由下行腔和上行腔构成，腔内充满油液并分别与外界油路连通，可通过油路中油液的进出控制腔内油量。在需要赋予火炮高低射角时，所有油路打开并向腔内注入油液：当向下行腔中注入油液时，高低机在下行腔油液压力作用下压缩，身管向下运动；当向上行腔中注入油液时，高低机伸长，身管向上运动；射击时，高低机的油口锁死，腔内油液不再与外界油路连通。在平衡机中，油路始终向平衡腔内供油以提供平衡力。平衡机力随支点距离的变化曲线如图3所示，其中平衡机上、下支点分别为与摇架和炮塔的铰接点。

在射击试验中，对高平机的上行腔和下行腔压力进行测量。在某射角下的测试状态如图4(a)所示，测试结果曲线如图4(b)所示，曲线中0.5 s为射击开始时刻。该曲线表明，在射击后，上行腔压力曲线首先出现了一个频率较小的压力脉冲，即高平机首先短暂受压；在后坐部分的第1个俯仰周期中，下行腔压力峰值约为200 kN，上行腔压力峰值约为155 kN；经过5个周期后，下行腔压力衰减至30 kN，上行腔压力衰减至40 kN。

2 全刚体模型的动力学仿真

以图4的测试结果作为校验仿真正确性的标准，计算该射角下的射击稳定性。对火炮进行发射动力学仿真分析，采用常规的多体动力学仿真方法，对射击时的火炮受力和运动状态作如下几点基本假设：各部件均为刚体，不考虑局部变形；不考虑各部件的间隙及尺寸误差，约束为理想约束；地面为水平硬质地面，不考虑地面变形；忽略旋转稳定弹丸的回转力矩影响。

目前基于火炮稳定性分析的发射动力学仿真计算基本均以以上几点假设为基本前提[6-7]。将火炮模型导入RecurDyn中，正确设置各部件之间的运动关系、接触、摩擦及相关系数，根据内弹道设计方案，在弹底-膛底间施加炮膛合力，在反后坐装置中施加后坐阻力。在参数设置过程中，需要计算高低机的刚度。由于上行腔和下行腔互不联通，因此可分别计算高低机的上行刚度和下行刚度，并分别施加于模型中。在计算过程中假设：不考虑油液对壁面的压力和摩擦力；油液假设为不可压缩流体，且忽略油液由于高平机行程变化所造成的体积弹性模量的改变；忽略缸体在油液压力作用下发生的变形[8]。

当油液腔处于拉伸状态时，拉伸阻力相当于外界大气压作用的压力。当油液腔被拉伸时，另一侧的油液腔受压，由于常用油液的体积模量在0.7～2.0 GPa之间，而空气的体积模量为0.143 MPa，因此，油液腔的拉伸刚度可忽略不计，即认为各腔在拉伸时不起作用。根据图1所示的模型结构及其几何尺寸，可计算得到各腔的截面积A以及长度L。当高低机整体拉伸时，下行腔油液受到压缩，上行腔油液不起作用。此时，下行腔刚度为

(1)

式中：KD为下行腔的刚度；E为油液的体积弹性模量；AD为下行腔的腔内截面积；LD为下行腔中油液长度；L为上、下支点之间的距离。

在不同射角下，L也随射角发生改变。根据设计方案，确定选用的油液后，E也随之确定，因此，可由式(1)计算得到高低机的下行腔刚度。同理，当高低机整体受压时，上行腔油液受到压缩，下行腔不起作用，此时，上行腔刚度为

(2)

式中：KU为上行腔的刚度；AU为上行腔的腔内截面积；LU为上行腔中油液长度。

在射击过程中，平衡腔不闭锁并始终提供平衡力。随着高平机拉伸-压缩过程中的行程变化，平衡腔提供的支撑力也将随之发生变化，其值可由图3的曲线确定。

经过仿真计算后，可得到射击后上行腔和下行腔的压力变化曲线如图5所示。

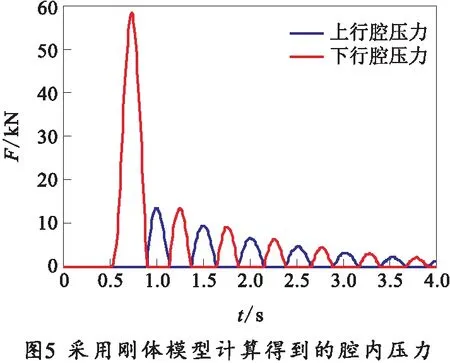
将图5与图4进行对比可发现该仿真结果与测试完全不符：仿真计算中的高低机首先在后坐力及后坐部分的惯性力等作用下受到较大拉伸，即受力方向与射击试验的测试结果相反；在后坐复进结束后，两腔压力的峰值仅为12 kN，不到测试结果的1/10。该模型使用了常规的多刚体动力学仿真方法，其结果无法反映高低机的真实状况，仿真结果不具备参考意义。

3 炮塔为柔性体的动力学仿真

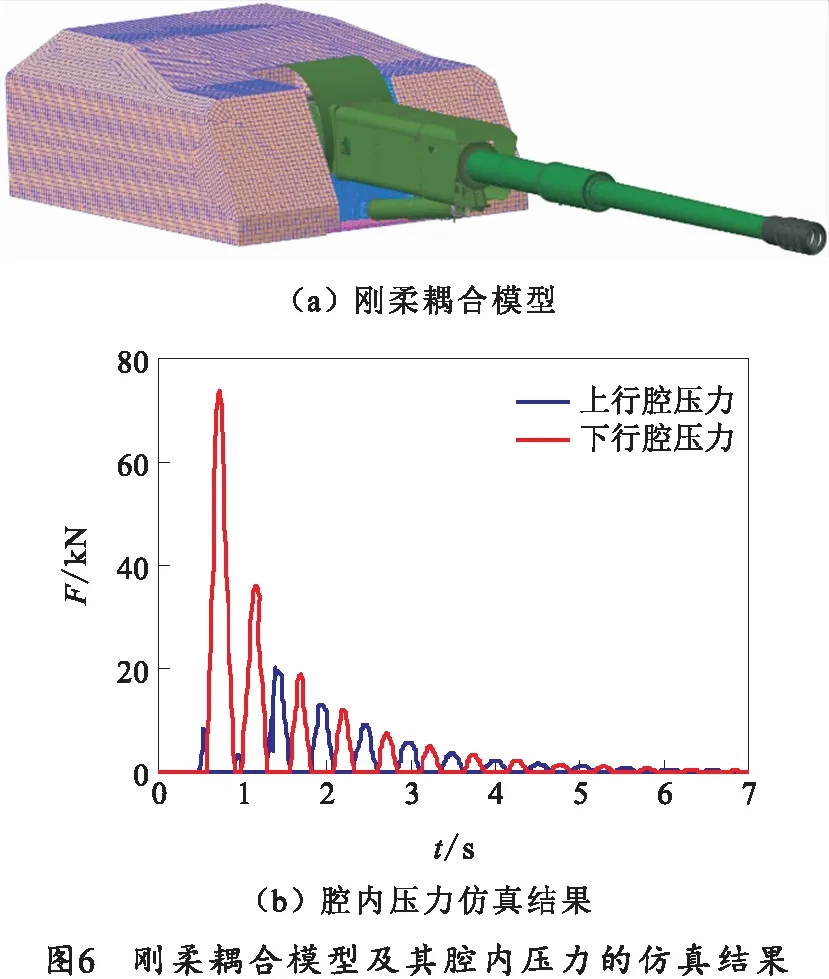
在射击试验的高速摄像中可以看到，发射过程中炮塔发生了肉眼可见的变形，因此，为判断仿真结果与测试结果不符的原因是否是由炮塔变形所引起，在仿真模型中考虑炮塔变形的影响，将多刚体模型中的炮塔替换为柔性体模型。划分有限元网格后，炮塔部分约有30 000个节点和80 000个单元，材料为钢，回转部分的刚柔耦合模型如图6(a)所示。对该模型进行动力学分析，得到上行腔和下行腔压力，如图6(b)所示。由该仿真结果可知，在考虑炮塔变形后，高平机首先受压，而且两腔压力都比图5有明显提高。但与图4对比，该仿真模型仍然无法正确反映高平机的实际工作状态，结果仍不具备参考意义。

4 考虑座圈晃动的动力学仿真

虽然座圈晃动会影响起落部分的俯仰状态，但因为晃动量很小，因而在火炮的设计过程中，往往认为其影响有限，在基本假设中定义这些装配区域均为紧密配合、不发生晃动和变形的理想状态[4-7]。然而，机床、机械臂等复杂机械产品的相关研究表明，结合部的弹性约束效应对一些机械产品的动力学特性有重要影响，如果将其视为理想刚性约束，则会导致分析结果存在较大误差[9]。如对机床的研究表明，机床总柔度的40%～60%是由结合面产生的[10]。在火炮系统中，座圈是连接上装与车体之间的重要结合部，特别是采用滚珠轴承的座圈，由于结构及制造等原因，座圈存在一定间隙，在射击过程中可能存在明显晃动并对射击稳定性带来较大影响。从高速摄像得到的视频片段中可以看到，该火炮在发射过程中，座圈的确出现了较明显的晃动。

在本模型中，考虑座圈晃动的影响因素。由于座圈采用的滚珠轴承中存在大量接触，计算收敛性差，耗费计算资源多，因此对座圈模型进行简化：忽略由于装配等因素导致炮塔和底盘上装甲板对座圈的加强作用，将炮塔底板和座圈单独导入ABAQUS中；将除后坐部分以外的回转部分的质量作为配重施加在模型中，即将该部分视为一个整体结构，后坐阻力为该结构的外力载荷；高平机力等为内力载荷，不考虑其造成的结构局部变形的影响。进行有限元计算，得到由于座圈晃动引起的炮塔底板晃动量情况。

座圈的计算模型如图7所示，座圈结构由装配于炮塔底部的上座圈、装配于底盘的下座圈和装配于上下座圈之间的滚珠构成。由于座圈为左右对称结构，为减小计算规模，取一半模型进行计算；将回转以上部分简化为配重；约束左、右对称面对称方向自由度和下座圈底部与底盘连接面3个方向自由度；为保证收敛性和计算精度，对滚珠与座圈接触部位进行了局部网格控制与加密。

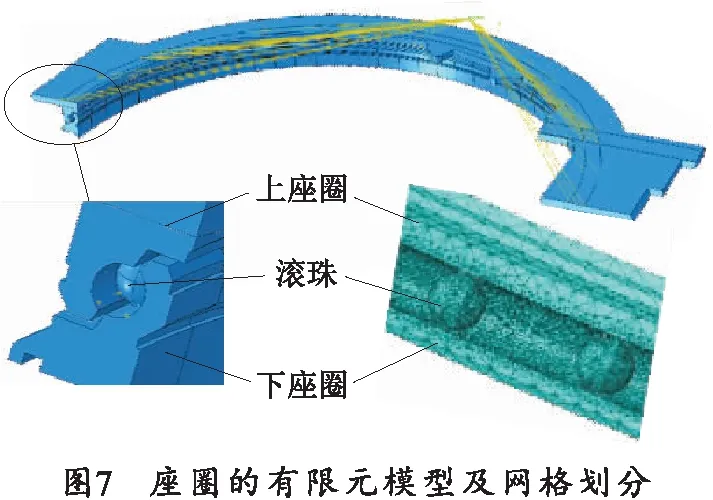
图8所示是仿真得到的座圈纵向最大变形云图及上座圈的俯仰角位移曲线。由图8可知，座圈的最大晃动量约为3.3 mrad。在RecurDyn的模型中以该仿真结果作为座圈晃动的边界条件，进行动力学仿真。

根据相关研究，结合部特性表现为既有弹性又有阻尼，既储存能量又消耗能量，可采用经典的弹簧和阻尼器等效法构建结合部的动力学模型[11-12]。如图9所示为该火炮模型中座圈结合部的等效动力学模型。在该火炮的座圈结构中，上座圈为外圈，固定于炮塔底部；下座圈为内圈，固定于底盘车体的上甲板中央。根据不同的射击工况，用至少前、后、左、右4组弹簧阻尼系统来模拟结合部的变形情况，每组弹簧阻尼系统均如图9所示，分别由水平和竖直两个方向上的线性弹簧和阻尼器构成。调整弹簧阻尼系统的刚度系数和阻尼系数，以保证射击时上座圈与下座圈之间的俯仰角位移与图8中的仿真结果相符。

考虑座圈晃动量但不考虑炮塔变形的影响，计算得到上行腔和下行腔的压力曲线如图10所示。对比图10与图4可知，曲线各峰值、频率等误差不超过15%，该结果可以正确反映高平机的实际工作状态。

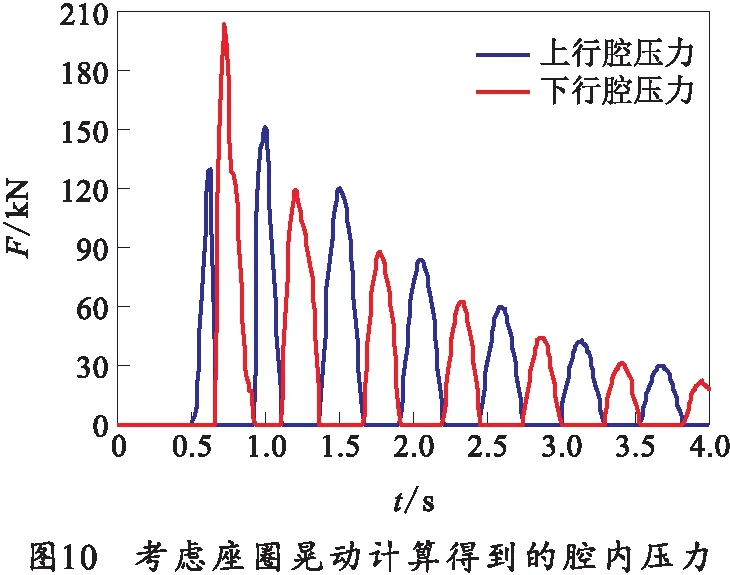
进一步同时考虑炮塔变形和座圈晃动对仿真结果的影响，计算得到的高低机腔内压力结果如图11所示。与图10对比可知，二者之间的误差很小。

图12所示是考虑座圈晃动后，分别采用刚性炮塔模型和柔性炮塔模型计算得到的回转部分的俯仰角。从该曲线中可以看出，两种计算模型的计算结果区别很小，进一步证明了炮塔变形影响较小，座圈晃动是影响仿真结果的主要因素。另外，在研究工作中，为了节省计算时间，可使用刚体模型进行仿真计算。

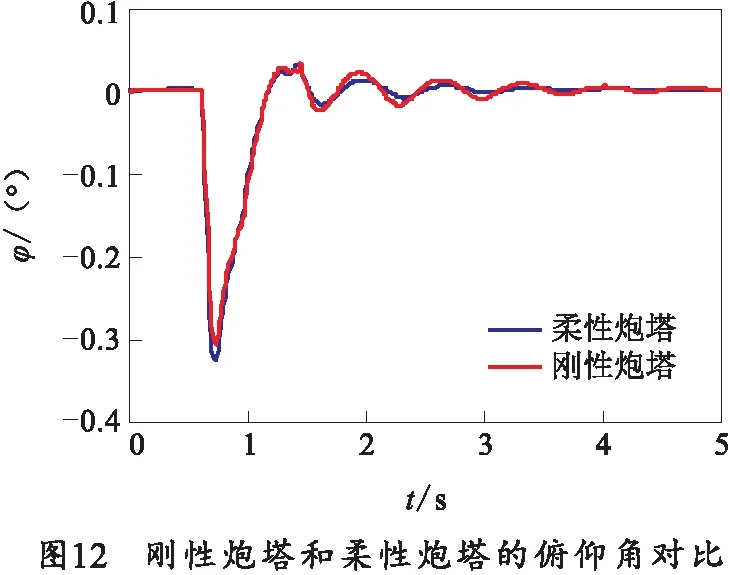
5 平衡机闭锁后的仿真结果

由射击试验的测试数据、高速摄像并结合图11和图12的仿真结果可知，在射击后，起落部分不能在短时间内恢复静止，影响供输弹的速度。考虑到射击时，平衡机仅由管路供油提供平衡机力，如果在平衡机油口处增加闭锁机构并在射击时闭锁，则可以进一步提高支撑刚度，从而提高火炮的射击稳定性。

将平衡腔闭锁后，平衡腔提供的初始力仍可由图3确定。当平衡机拉伸时，平衡机力不断降低，直到为0，此后如果继续拉伸，平衡腔内油液将不再起作用。由流体动力学可知，当液体压力变化Δp时，液体体积改变量ΔV为

(3)

式中，V为平衡机内油液体积。

根据式(3)可反算得到压力为0的位置以及压力随行程的变化规律。由于初始压力为

(4)

则式(3)可变为

(5)

式中：Fc即为相应射角下平衡腔提供的初始平衡力；F′为发射过程中高平机行程改变ΔL之后平衡腔内油液提供的力。

将数值带入计算得

(6)

即可得到当F′大于0时随ΔL的变化规律，当F′减小至0以后，平衡腔不再起作用。

当高平机压缩时，平衡腔被压缩，除初始平衡机力作用外，腔内油液刚度为

(7)

即当平衡腔压缩时，式(6)中的刚度项的符号为正：

(8)

平衡腔闭锁与不闭锁时的后坐部分俯仰角曲线如图13所示。由图13可知，在平衡腔不闭锁时，射击后起落部分需要约8 s左右才能完全恢复静止；而平衡腔闭锁后，射击后的3.5 s左右即可恢复静止。提取两模型中的高平机伸缩量曲线如图14所示，可知在平衡腔闭锁以后，高平机的最大伸缩量由闭锁前的21 mm下降到6 mm，下降了71%；而平衡腔不闭锁与闭锁的后坐部分的最大俯仰角分别为2.4°和1.9°，仅相差21%。图13中的后坐部分俯仰角是以车体为参考对象的，即：起落部分的俯仰角是炮塔相对于座圈的俯仰角与起落部分相对于炮塔的俯仰角的二者之和；由于平衡腔是否闭锁对高平机的伸缩量影响明显大于对后坐部分俯仰角的影响，说明在起落部分的俯仰角中，起落部分相对于炮塔的俯仰角占比较小，炮塔相对于座圈的俯仰角占比较大，但炮塔相对于座圈的俯仰动作更容易衰减至静止状态。

平衡腔闭锁后的各腔压力曲线如图15所示。对比图15和图10可知，在平衡腔闭锁后，下行腔压力最大峰值由190 kN下降到了56 kN，下降了71%；上行腔压力最大峰值由159 kN下降到了30 kN，下降了81%；而平衡腔压力由基本保持常值的99 kN上升到最大峰值力424 kN，上升了327%。即在平衡腔闭锁后，高平机的支撑力主要由平衡腔承受，且平衡腔力峰值上升较大。如果后续采取该改进方案，则必须对平衡机及其相关联的部件进行刚强度校核。但相比于高低机的双腔结构，平衡机的单腔结构相对简单，更容易进行结构上的增强。另外，平衡机的受力高于高低机，是由于平衡机的刚度更高导致的，因此，在进行改进设计时，可根据式(7)计算的平衡腔油液刚度，通过更换低压缩模量的液压油或增加油腔长度等方式，降低平衡机闭锁时的刚度，均衡平衡机和高低机各腔的压力分布。

6 结束语

火炮发射动力学仿真是贯穿于火炮装备方案设计、问题分析以及后续改进过程的重要技术手段，通过建立合理简化的计算模型得到误差可接受的计算结果是分析问题的前提。笔者针对传统仿真方法中所采用的假设部件之间为理想约束、不考虑结合部晃动的模型，无法得到某大口径火炮高低机受力及运动状态的正确仿真结果的问题，依次考虑了炮塔变形以及座圈晃动的因素并进行了相关仿真计算。计算结果表明，是否考虑座圈晃动是影响该火炮高低机腔内压力计算结果的最主要因素，

在采用弹簧阻尼系统模拟座圈晃动后，能够将仿真误差有效控制在15%以内。在建立正确的模型后，对原设计方案进行改进，采用闭锁平衡腔的方式，能够有效提升火炮的射击稳定性，但需要对相关部件重新进行刚强度校核，或对结构尺寸进行优化设计进而均衡各腔压力分配。研究内容加深了对火炮发射动力学仿真模型的认识，完善了火炮动力学仿真方法，提高以后工作中仿真计算的精度，增强了仿真对火炮方案设计和改进设计的指导作用。