电网不平衡条件下模块化多电平变换器控制策略
牛帅臣,王福忠,韩耀飞,何国锋,牛叶克
(1.河南理工大学 电气工程与自动化学院,河南 焦作 454000;2.河南城建学院 电气与控制工程学院,河南 平顶山 467036)
随着高压直流输电中电压等级的不断提高,基于模块化多电平变换器(Modular Multilevel Converter,MMC)的柔性直流输电技术得到了快速发展[1]。在工业应用中最常见的拓扑结构是级联H桥型(Cascaded-H-Bridge,CHB)[2]和中性点钳位(Neutral-Point-Clamped,NPC),但这些拓扑存在一些不足,例如级联H桥型拓扑需要体积较大的变压器,中性点钳位型拓扑中电压等级受到限制。MMC由于具有传输效率高与电能品质好的优点,已成为研究与应用的热点[3-4]。与传统的电压源型变换器(Voltage Source Converter,VSC)相比[5-6],MMC具有高度模块化、可扩展、效率高、输出电压纹波低、故障保护能力强等优点。但MMC也存在电容电压不平衡和相间环流等问题。由于模块化多电平变换器中的子模块采用分布式串联结构,需要不断地对电容进行充放电,相间的能量不能保证完全一致,导致产生相间环流[7],不仅增加了损耗,严重时还会导致器件损坏,所以必须对MMC环流进行抑制。目前大部分研究是基于电网电压平衡下模块化多电平的研究[8-12]。当电网电压不平衡时,三相环流将会出现二倍频正序、负序和零序分量,零序环流分量流入MMC直流侧,使直流侧出现二次脉动,影响电能的品质。由于MMC平衡条件下的控制策略并不适用于电网电压不平衡的情况,因此国内外也展开了对不平衡电网下MMC控制策略的研究。
文献[13]提出了一种基于比例降阶谐振调节器的MMC不平衡控制策略,但该方法只能抑制零序环流。文献[14]提出了一种无源控制策略,用于控制交流侧三相电流不对称、有功、无功功率出现的二次脉动问题。文献[15]对电流正、负序量进行分离,并采用PI进行控制,但PI控制动态性能差。文献[16]采用比例积分与准谐振控制器相结合的方式对电流内环进行控制,在同步旋转坐标系下对正、负序电流进行统一控制。文献[17]采用并联的矢量比例积分调节器和比例积分调节器对环流进行抑制,但该策略应用范围有限。文献[18]提出基于PI调节器的环流抑制策略,但该策略的控制性能并不理想。
自抗扰控制器(Active Disturbance Rejection Controller,ADRC)技术利用扩张状态观测器(Extended State Observer,ESO)对系统内部和外部的扰动进行估计补偿,其响应速度快、控制精度高,具有较强的抗干扰性。本文针对电网电压不平衡条件下MMC存在的环流问题设计了一种基于线性自抗扰控制器的环流抑制方法。本文首先对MMC的主电路进行分析,指出不平衡故障时MMC内部存在二倍频环流,得出桥臂电流与环流之间的关系和环流参考值的计算式;然后,对线性自抗扰控制器的原理以及参数的整定进行介绍,并结合MMC控制原理对环流进行抑制;最后,在MATLAB/Simulink中搭建系统仿真模型,验证了该控制策略的有效性。
1 MMC环流分析
1.1 MMC的拓扑结构
MMC主电路以及子模块如图1所示,分为a、b、c三相,其中每相由上、下桥臂构成。每个桥臂由n/2个子模块(Submodule,SM)与电抗器L0串联组成。桥臂电抗起抑制相间环流和冲击电流的作用。子模块由两个IGBT、两个反向二极管和一个电容器组成。T1和T2控制信号互补,当T1导通,T2关断时,输出电压为Uc;当T1关断,T2导通时,输出电压为零。
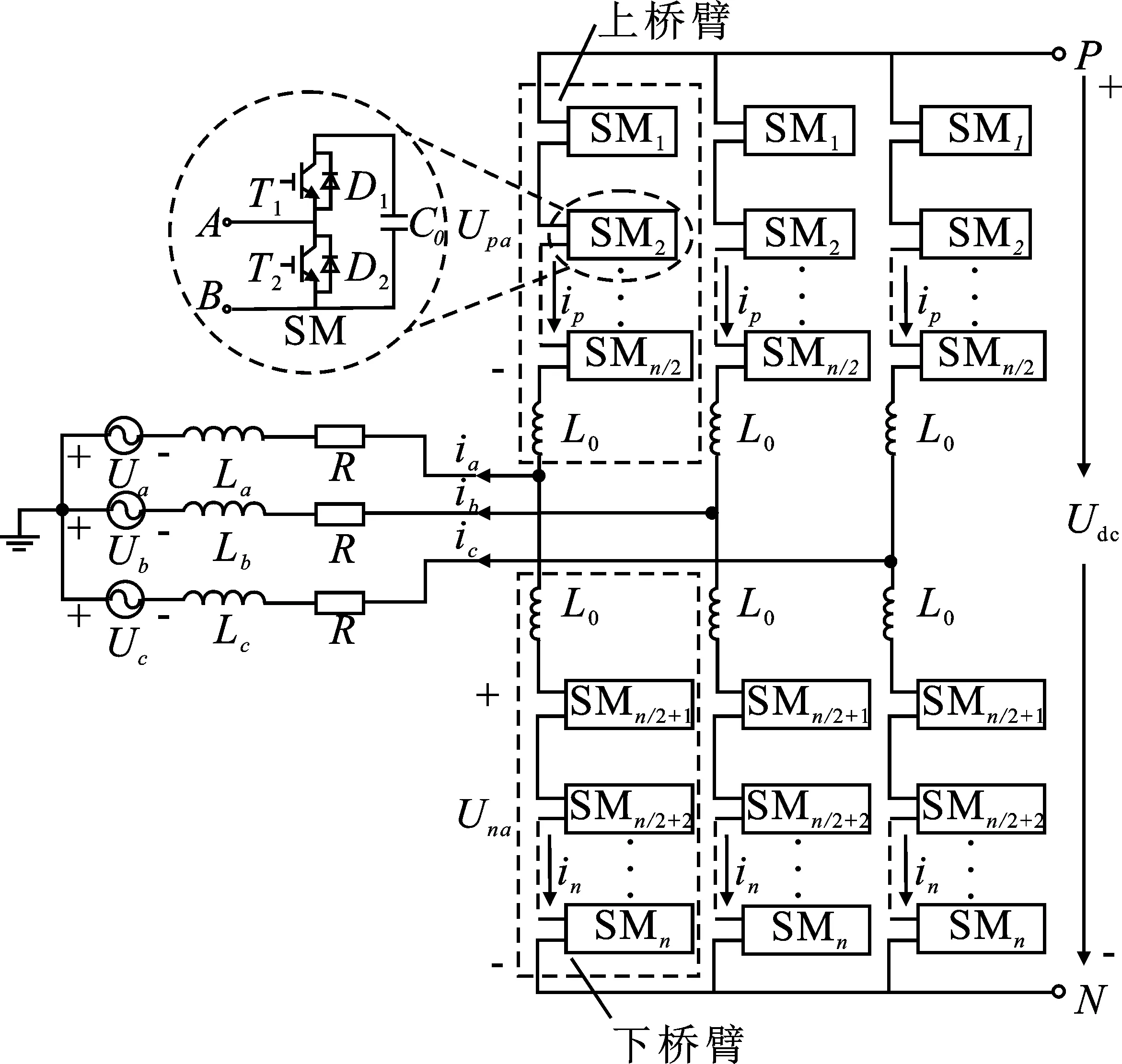
图1 MMC主电路及子模块结构图Figure 1. The main circuit and submodule block of MMC
1.2 MMC的数学模型
图2为MMC其中一相的等效模型。上、下桥臂的子模块等效为交流源,上桥臂电压为Upx,下桥臂电压为Unx(x=a,b,c)。直流总线等效为连接公共点的两个串联的直流电源。在理想情况下,桥臂电流是基频的直流分量和交流分量之和,流过上桥臂的电流为ip,流过下桥臂的电流为in。由于交流电流流过子模块电容器,电容器电压随时间而变化,直流母线电压与每相电压之间存在电压差,导致相间产生环流。
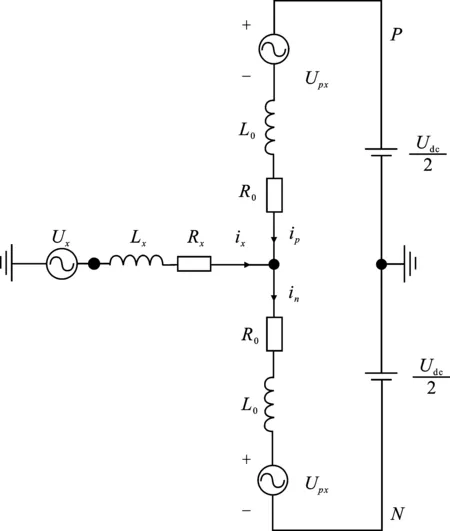
图2 MMC等效模型Figure 2. Equivalent topology for MMC
桥臂电流可以表示为[10]
(1)
式中,icirx为内部环流;ix为交流侧断面线电流。
由式(1)可得
(2)
MMC的数学模型可以表示为
(3)
(4)
在式(3)中,不妨假设
(5)
将ex称为x相的虚拟电动势,式(3)实际上是代表MMC外部特性的特征方程。
对MMC的控制,实际就是控制各相上、下桥臂的输出电压Upx和Unx。由式(4)和式(5)可知,对内部环流的间接控制并不会影响x相的虚拟电动势ex,即MMC的外特性不变。本文根据这一情况设计对应的内部环流抑制控制器(Circulating Current Suppressing Controller,CCSC)。
根据式(4)和式(5)可以得到上、下桥臂电压的参考值为
(6)
式中,Ucirx表示内部不平衡电压,可以从环流抑制器中获取;ex可以由系统级控制器获得。
1.3 电网不平衡时MMC瞬时功率分析
MMC与电网电压之间采用Y/Δ接线方式,不存在零序分量。当电网电压不平衡时,交流输出侧电压和电流可以表示为
(7)
式中,EP、EN、IP、IN分别为电压、电流的正、负序幅值;θP、θN、ψP、ψN分别为电压、电流的正、负序初相角;ω为电网角频率。
根据瞬时功率理论可知,MMC交流侧a相瞬时功率可以表示为
pa=upaipa+unaina=eaia+(Udc-2ucira)Idca
(8)
由于ucira相对于Udc可以忽略不计,因此
pa=eaia+UdcIdca
(9)
式中,Idca表示为a相环流的直流分量。
pa还可以表示为
(10)

其中环流的直流分量可以表示为[17]
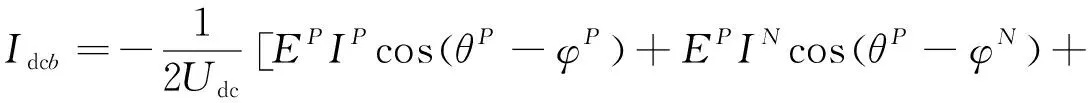
(11)
(12)
(13)
环流的直流分量可以进行有功传输,因此需保留环流的直流分量而消除环流交流二倍频分量。
2 线性自抗扰控制器原理
为了消除电网电压不平衡条件下出现的二倍频正序、负序和零序环流分量,本文提出基于线性自抗扰控制器的环流抑制策略。自抗扰控制技术继承并发扬了PID控制思想的精髓,具有抗干扰性强、响应速度快、鲁棒性强等优点[19-20]。自抗扰控制器主要由跟踪微分器(Tracking Differentiator,TD)、非线性状态误差反馈率(Non-Linear State Error Feedback Rate,NLSEF)和扩张状态观测器(ESO)组成[21],其基本结构如图3所示。
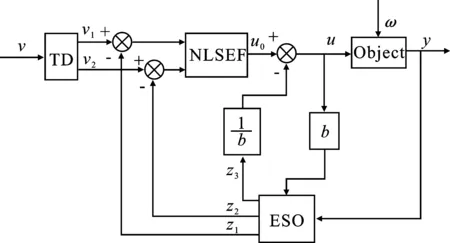
图3 自抗扰控制器基本结构Figure 3. The basic structure of ADRC
跟踪微分器通过合理提取微分信号并根据被控对象的承受能力合理安排过渡过程,从而有效地协调系统输出快速性与超调之间的矛盾。扩张状态观测器是根据外部变量的观测来确定系统内部状态变量的一种装置。它的功能是利用系统的输入信号与输出信号来确定系统内部所使用的状态信号,对不可测参数的获取提供近似估算的方法。
建立如图3所示的线性扩张状态观测器
(14)
当输出误差校正系数β1、β2、β3为合适值时,则有
(15)
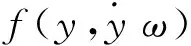
(16)
设TD控制器为
u0=KTv-z1-KDz2
(17)
式中,v为给定信号;KT和KD为控制器增益。由式(14)~式(17)可得传递函数为式(18)。
(18)
综上可以建立二阶系统的线性自抗扰控制器(Linear Active Disturbance Rejection Controller,LADRC),其结构如图4所示。
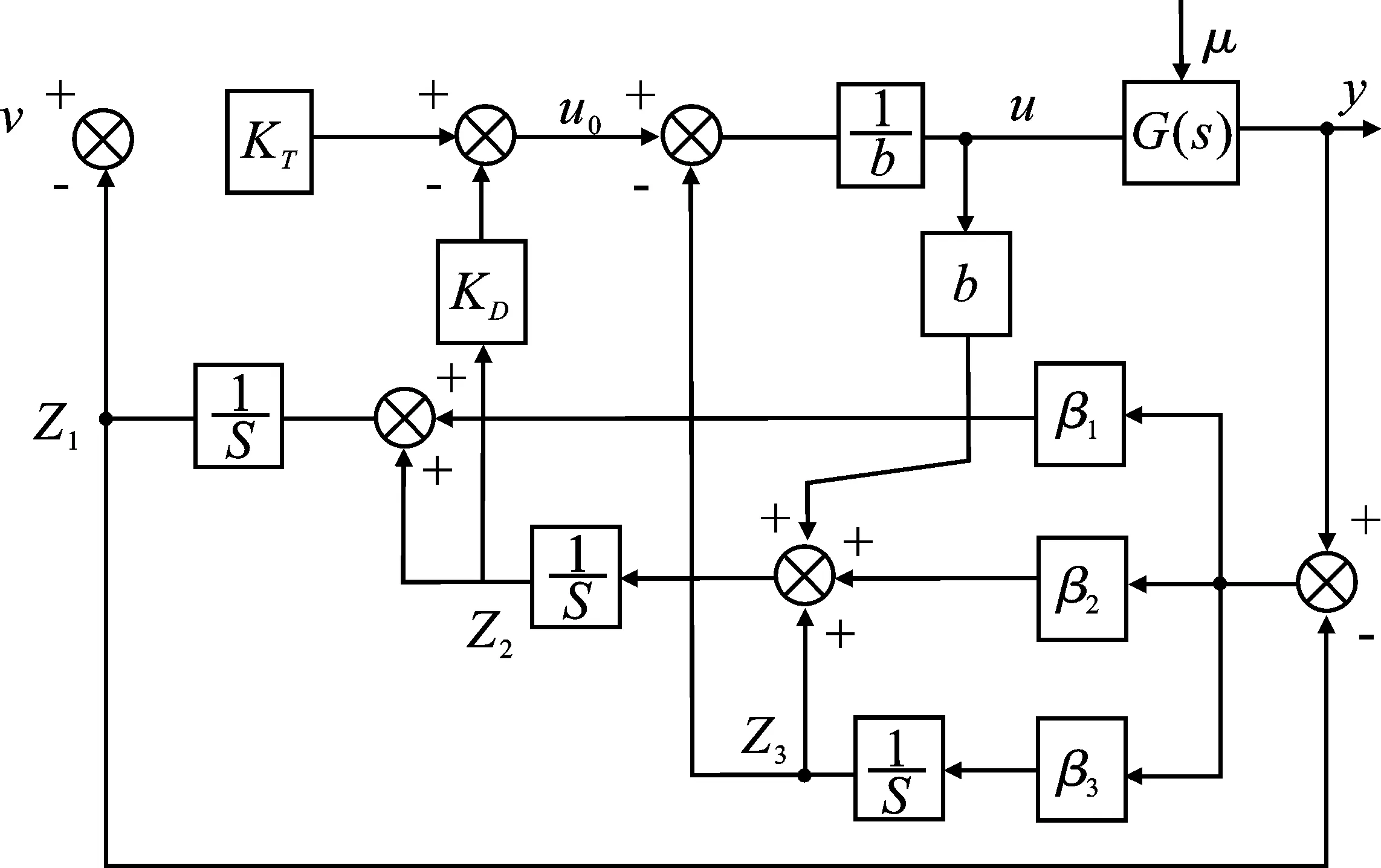
图4 LADRC结构图Figure 4. The structure of LADRC
其中,β1=3ω0,β2=3ω02,β3=ω03,KT=ωc2,KD=2ωc,ω0为观测速带宽,ωc为控制器带宽,这样可以简化参数的设计,从而缩短自抗扰控制器参数整定的过程。
3 基于ADRC的MMC控制策略
与传统PI控制器相比,自抗扰控制器不依赖于受控对象的精确数学模型,对于系统的不确定性具有较强的鲁棒性,同时具有较强的抗干扰性。根据上、下桥臂电流计算出相间环流icirx作为输出信号。由式(11)~式(13)得到环流的直流分量值Idcx,并将其作为输入信号。自抗扰控制器可以保证对环流的直流分量无静差跟踪。
图5为MMC的整体控制框图。MMC分为3个部分:环流抑制部分、主控制部分和调制触发脉冲部分。环流抑制部分通过MMC数学模型计算出上、下桥臂电流,由式(2)可计算出作为输出信号的相间环流icirx。通过瞬时功率计算出环流的直流分量参考值Idcx,将其作为输入信号。将比较后的误差信号输入线性自抗扰控制器后将会得到环流不平衡压降的参考值Ucirxref。
主控制部分采用双dq-PI控制器,对MMC交流侧的正、负序电流进行控制。为了消除负序电流,设定负序电流的参考值为零。通过有功参考值和无功参考值的计算,可以得到正序电流参考值的表达式为[22]式(19)。
(19)
根据式(6)得到上桥臂的参考电压Upxref和下桥臂的参考电压Unxref。通过载波移相调制策略得到子模块通断的触发脉冲,从而得出控制系统子模块的接入时间。
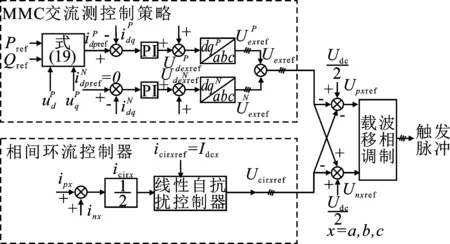
图5 含LADRC的MMC总控制结构图Figure 5. The structure of MMC master control with LADRC
4 仿真结果与分析
为了验证本文所提出的自抗扰参数的准确性,在MATLAB/Simulink平台搭建了5电平的MMC仿真模型。本文所采用的线性自抗扰控制器仿真参数如表1所示。
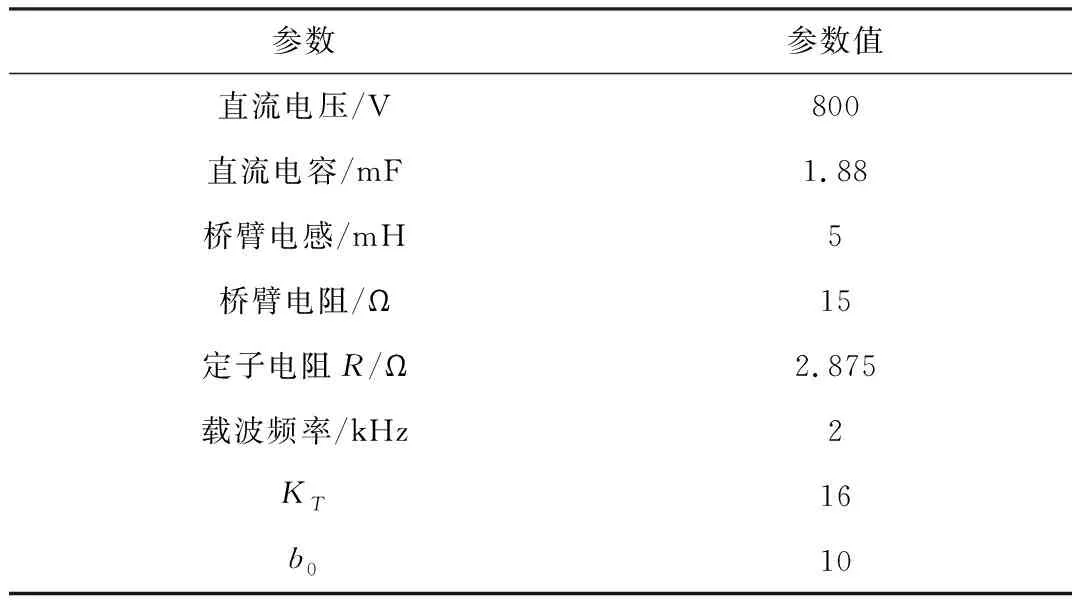
表1 仿真参数模型
为了验证ADRC在电网不平衡下的环流抑制效果,本文对PI控制的环流抑制策略和本文提出的ADRC环流抑制策略进行对比。

(a)

(b)
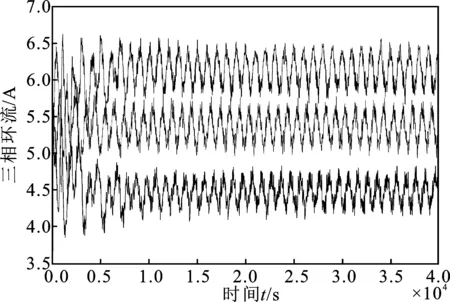
(c)
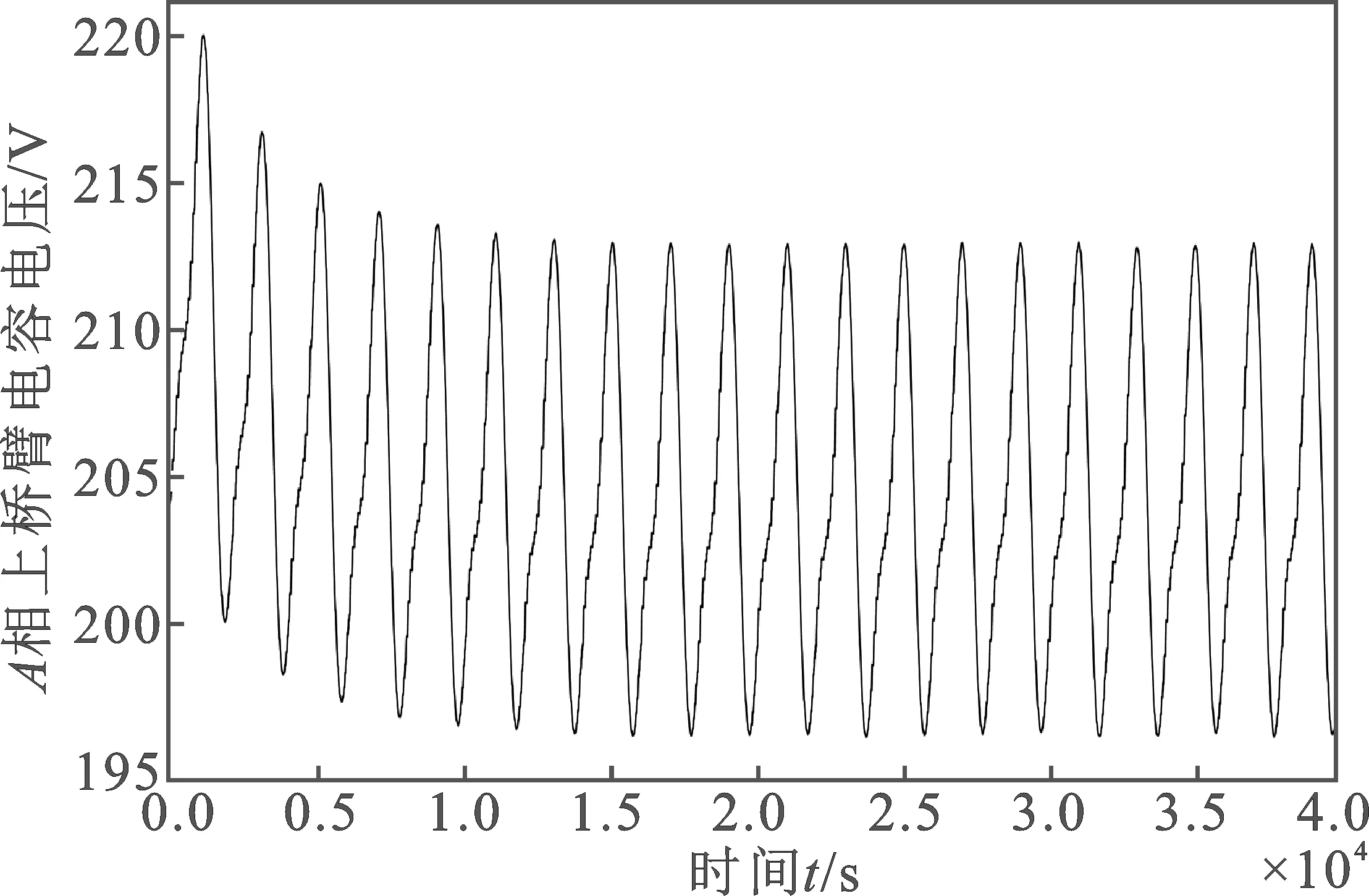
(d)图6 PI环流抑制控制器仿真结果Figure 6. Simulation results of circulating current suppressing controller based on PI control

(a)
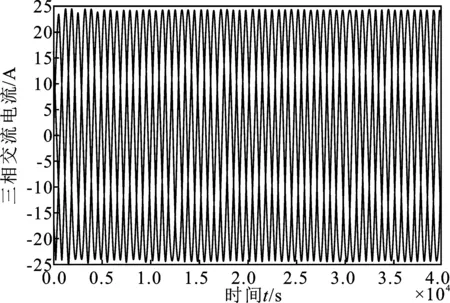
(b)

(c)
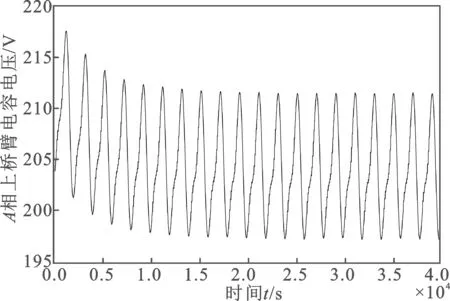
(d)图7 ADRC环流抑制控制器仿真结果Figure 7. Simulation results of circulating current suppressing controller based on ADRC
当A相电压发生30%的电压跌落导致电网电压不平衡时,由图6(c)和图7(c)可知,在0.5 s之后,线性自抗扰控制器比PI控制器具有更好的环流抑制效果。由图6(d)和图7(d)中A相上桥臂电压可得,加入PI环流抑制控制器后,Uc的波动范围为196~215 V;而加入ADRC后,Uc的波动范围为198~213 V,PI控制器比ADRC波动范围大。该结果表明线性自抗扰控制器具有更强的抗扰动性。采用线性自抗扰控制器时,环流波形快速趋于平稳则说明线性自抗扰具有较强的响应速度。
5 结束语
本文针对电网电压不平衡条件下MMC存在的环流问题设计了一种基于ADRC的环流抑制策略。首先对MMC环流模型进行了分析,根据瞬时功率理论推导出不平衡电网下环流的直流分量表达式。然后,采用ADRC对环流进行精确控制,并与现有PI环流控制策略进行对比,发现其不依赖于受控对象的精确数学模型,简化了参数的设计。最后,MATLAB/Simulink仿真验证了所提设计环流抑制控制器具有良好的控制效果。MMC往往用于大功率的场合中,将ADRC加入其中后,需要对其复杂控制情况进行考虑,因此未来仍需要对其控制精度进行研究。

