基于图卷积网络和门控循环单元的多站点气温预测模型

马栋林，马司周，王伟杰

（兰州理工大学计算机与通信学院，兰州 730050）

0 引言

天气现象与农业、水资源、交通、经济以及人们日常生活等诸多方面息息相关，据瑞再研究院报告［1］称，受天气变化影响，恶劣天气事件所造成的损失不断增加，在未来的几十年里，此类事件造成的经济损失将不断上升。如何通过准确预测天气变化减小损失成为目前亟须解决的问题。

气象预测方法从依靠个人经验到简单的数值方法，再到复杂的大气物理模型，已经走过了很长的路。近年来，气象数据不断增长，如何有效利用海量的气象数据来减小预测误差成为气象预测研究的重点，研究者们开始使用机器学习方法预测未来天气变化。Liu 等［2］和Kwong 等［3］提出了使用人工神经网络进行风力预测，实验结果表明，该方法能有效捕捉香港国际机场附近滑翔处的风速变化。Krishnaveni 等［4］提出了基于决策树的SPRINT（Scalable PaRallelizable INduction of classification Tree）算法进行天气预测，实验结果表明，SPRINT 算法对天气状况的预测是有效和准确的。深度学习作为机器学习的一个重要分支，已在语音、图像、视频、交通等众多领域取得成功［5-6］，因此一些研究者在传统机器学习方法的基础上，开始使用深度学习方法进行气象预测研究。Hossain 等［7］利用内华达州西北部气象传感器收集的历史气压、湿度和气温数据，使用堆叠降噪自编码器（Stacked Denoised AutoEncoder，SDAE）来预测气温，结果表明，SDAE 优于标准的多层前馈网络；Li 等［8］提出了一种端到端的集成时空注意力网络和多层感知机混合的回归模型，对北京地区24 个自动气象站的地面温度、湿度、风速和风向进行了预测，结合历史观测数据和数值天气预报（Numerical Weather Prediction，NWP）系统的数据，所提出的模型比NWP 系统有更好的预测结果；Jia 等［9］提出了一种基于注意力的序列到序列的臭氧浓度预测模型，实验结果表明，该模型比以化学为基础的天气研究和预测模型更简单、效果更好；Wei［10］比较了深层神经网络包括多层感知器（Multi-Layer Perceptron，MLP）、深层循 环神经网络（Deep Recurrent Neural Network，DRNN）和堆叠长短期记忆（Long Short-Term Memory，LSTM），结果表明，使用堆叠LSTM 模型，对台湾东北部台风的预测效果最好；Kim 等［11］提出了一种结合去噪自编码器和卷积长短期记忆的深度学习模型来预测全球海洋天气，实验结果表明，所提出的模型在海洋天气预报中适用性良好；Ham 等［12］使用卷积神经网络（Convolutional Neural Network，CNN）预测提前一年半的厄尔尼诺现象，实验证明，CNN 模型的Nino3.4 指数的全季相关能力远高于目前最先进的动态预报系统，同时，CNN 模型也能更好地预测海表温度的详细纬向分布，克服了动态预测模型不能准确预测海表温度的详细纬向分布的这个缺点；Chhetri 等［13］出了一种基于双向长短期记忆网络（Bidirectional Long Short Term Memory，BLSTM）和门控循环单元（Gated Recurrent Unit，GRU）的月度降水预测（BLSTM-GRU）模型，并将其结果与深度学习中先进的方法进行了比较，结果表明，与线性回归、MLP、CNN、LSTM 和GRU 等模型比较，BLSTM-GRU 方法具有更低的预测误差。

从以上基于深度学习的气象预测方法可以发现，气象数据具有明显的高维特征，因此相比传统的BP（Back Propagation）神经网络，具有多层结构的深度神经网络更适合进行气象预测［14］。同时，气象数据作为典型的时序数据，使用处理时间序列的深度学习方法（如LSTM、GRU 等）要明显优于普通模型。然而，现有的深度学习方法大多只考虑单一的时间因素影响，忽略了气象观测站间的空间地理位置影响［15］，为了说明空间因素的重要性，图1 展示了一个例子。站点2、3 气温相近，但与站点1 气温相差较大，其原因是站点2、3 的空间地理位置相近，彼此之间空间相关性大，相反站点1 与站点2、3 的空间距离相远，空间相关性小。因此，如果能将附近地区的气象变化信息纳入模型，将有助于降低预测的误差。

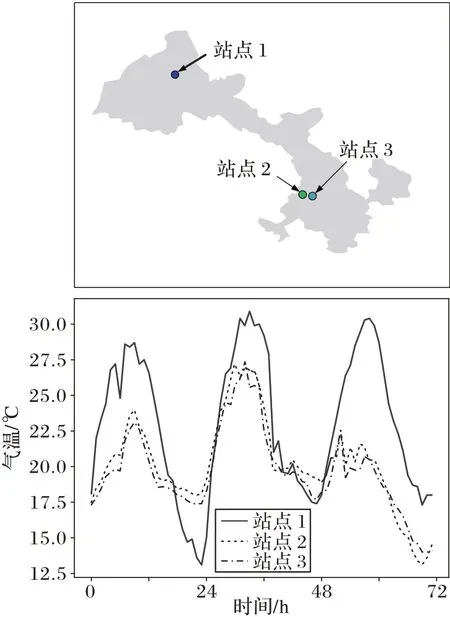
图1 气温受空间地理位置影响Fig.1 Temperature affected by spatial and geographical location

综上所述，针对现有的基于深度学习的气温预测方法误差大、时空特征提取不充分的问题，本文选取气象观测站点地理位置数据和气温数据进行建模，提出一种基于图卷积神经网络（Graph Convolutional Network，GCN）和门控循环单元（Gated Recurrent Unit，GRU）的气温 预测模 型（Graph Convolutional Network and Gated Recurrent Unit，GCN-GRU）。首先，使用重新分配权重和多阶近邻连接方式修正传统的GCN；然后，将GRU 中每个门控循环单元的矩阵乘法换成改进的GCN 操作，并将所有的门控循环单元串联，构成图卷积门控层；接着，使用图卷积门控层搭建网络主体结构，用于提取数据的时空特征；最后，使用一个全连接的输出层输出气温预测结果。

1 理论基础

1.1 气温预测问题定义

气温预测是典型的时间序列预测问题，即，给定H个时间步长的气温观测数据值，预测接下来M个时间步长的气温值：

其中，vt∈RN为t时刻N个气象站点的气温观测值向量，vt中每个元素记录单个气象站点的历史观测数据；P为概率函数。

传统的深度学习方法使用单个气象观测站点数据进行建模预测。本文考虑到气象观测站之间的空间影响，将一个地区的多个气象观测站建模成图网络。因此，本文从时间和空间两个角度分析气温预测问题，使用GCN 提取气温数据的空间特征，使用GRU 提取气温数据的时间特征。

1.2 GCN

近年来，由于交通网络、万维网和社交网络等多种图数据的出现，研究人员开始关注如何在图上构造深度学习模型，图卷积神经网络成为了处理图数据的有力工具。目前图卷积神经网络的主流方法分为两类［16］：一类是谱域图卷积，主要利用了图谱理论和卷积定理，将数据由空域转换到谱域作处理，处理完后再使用傅里叶逆变换转换回空域［17］；另一类是空域图卷积，这类方法绕开图谱理论，直接在空间上定义卷积操作［18-20］。前者对图滤波器的设计具有显式的公式指导，但是对矩阵进行特征分解具有O(n3)的时间复杂度；后者定义直观，灵活性更强，时间复杂度更低，具有工程上的优越性。因此本文选用空域图卷积方法建模气象数据图网络。

为了定义图卷积，首先将气象数据图网络定义为G=(V，E，W)，V∈RN为节点集合，即气象数据图网络中所有气象站点组成的集合；E∈RN×N代表所有边的集合；W∈RN×N为加权邻接矩阵，表示节点间的关系；度矩阵Dii=。然后依据图谱理论推导图卷积（GCN）［18］，利用邻接矩阵W和度矩阵D定义图的拉普拉斯矩阵L：

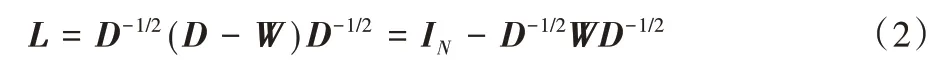
其中：IN为N阶的单位矩阵，L为实对称矩阵，从而必然存在对角矩阵Λ=diag(λ1，λ2，…，λN)与L相似，即存在正交矩阵U使得L=UTΛU。接着利用傅里叶变换和傅里叶逆变换得出谱域的图卷积定义：

其中：X为输入的特征矩阵；h为定义的卷积核；⊙表示哈达玛积；F和F-1分别为傅里叶变换和傅里叶逆变换。最后利用切比雪夫多项式对式（3）进行一阶近似估计，得到GCN 图卷积如式（4）所示：

1.3 GRU

标准的循环神经网络（Recurrent Neural Network，RNN）在训练过程中存在梯度消失和梯度爆炸问题［22］，使得RNN难以实现信息的长期保存，长短期记忆（Long Short-Term Memory，LSTM）网络［23］通过引入记忆单元和门控单元保存历史信息，但是LSTM 的内部结构复杂，模型训练时间开销过大。因此本文参考Cho 等［24］提出的方法，使用门控循环单元（GRU）捕获气温数据的时间动态变化特征。GRU 将LSTM 单元中的输入门和遗忘门合并为更新门u(t)，用于控制隐藏状态的更新，重置门r(t)用于判断是否保留之前的隐藏状态，GRU 的前向传播计算如式（5）～（8）所示：

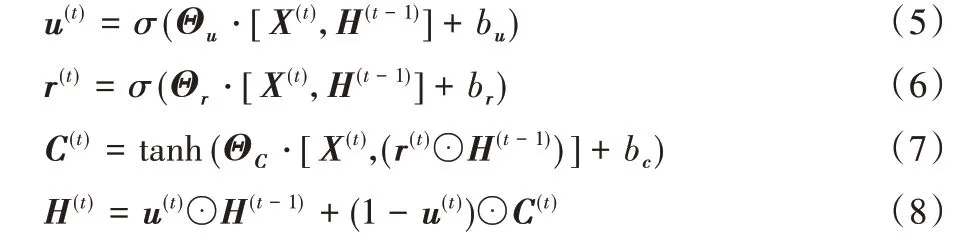
其中：X(t)为t时刻的输入；H(t-1)为t-1 时刻的隐藏状态；C(t)、H(t)分别表示t时刻的候选隐藏状态和隐藏状态；σ为sigmoid 激励函数；⊙表示哈达玛积。

2 模型设计

2.1 构建邻接矩阵

邻接矩阵是构建图的重要步骤，本文使用气象观测站作为节点并通过观测站之间的距离构建邻接矩阵，对于每两个气象观测站间的距离计算如式（9）所示：

其中：dij为节点i到节点j的实际距离；R为地球半径；Lati、Longi分别为节点i的纬度和经度；b=Longi-Longj、a=Lati-Latj分别表示两节点经纬度之差。用W表示气象数据网的加权邻接矩阵，W的定义如式（10）所示：

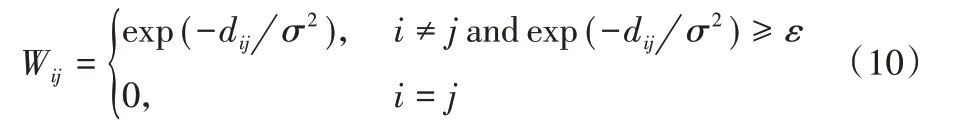
其中：Wij为利用距离dij计算出的边的权值；σ2和ε用于控制加权邻接矩阵W的分布和稀疏性，分别取10 和0.5［6］。

2.2 修正GCN

1.2 节介绍了GCN 的基本操作，即对每层网络的输出，都有如式（4）所示的计算。对于图中的任意节点而言，节点特征每更新一次，就会多聚合更高一阶邻居节点的信息，这有利于捕获数据空间关系，如果把最高邻居节点的阶数称为该节点的聚合半径，那么随着GCN 层数的增加，节点的聚合半径也在增长，一旦到达某一阈值，会导致节点的输出特征过度平滑［25］。为了防止过平滑现象发生，GCN 的层数一般会设置成1～2 层，然而浅层的GCN 又不能有效地传播节点信息。因此，为了使GCN 能更好地在气象数据中发挥作用，本文对GCN 做了以下两点修正［20，25-26］：

1）重新分配权重，增加邻接矩阵W中节点自连接边的权重［27］：

具体来说，将式（10）定义的邻接矩阵W引入了一个参数p∈[0，1]，如式（11）所示，通过调节p的值对节点自身权重进行重新分配。当p接近1 时，模型趋向于不使用自身节点的信息；当p接近于0 时，模型趋向于不聚合邻居节点的信息。

2）多阶近邻连接，扩大图卷积的感受野［20］：

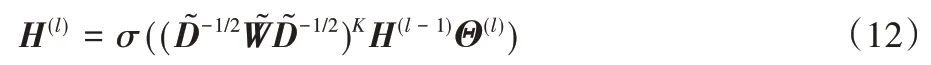
2.3 网络结构

本节描述GCN-GRU 模型的基本组件和实现步骤。GCN-GRU 模型的网络结构如图2 所示，由1 个输入层、3 个图卷积门控层（Graph Convolutional Gating Layer）和1 个全连接的输出层组成，其中图卷积门控层由GCN 和GRU 组成。下面详细介绍GCN-GRU 模型的实现步骤。

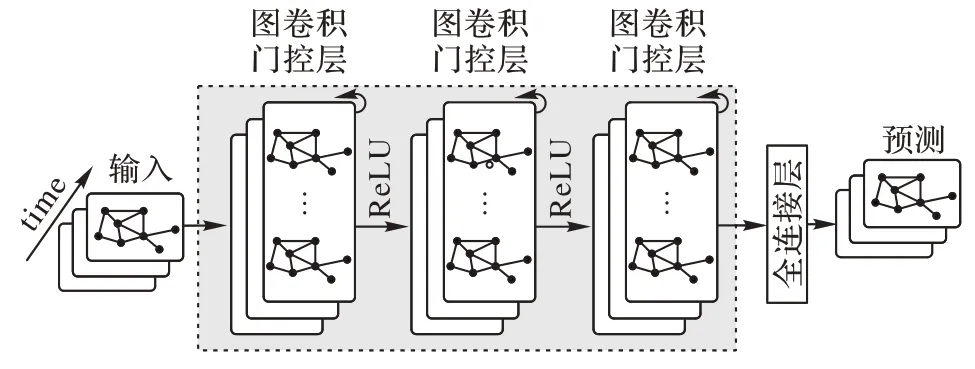
图2 GCN-GRU网络结构Fig.2 Network structure of GCN-GRU

步骤1 将GRU 循环单元的更新门u(t)、重置门r(t)以及候选隐藏状态C(t)中的所有矩阵乘法，换成本文2.2 节修正的GCN 操作，每个循环单元的数学表达如式（13）～（16）所示：

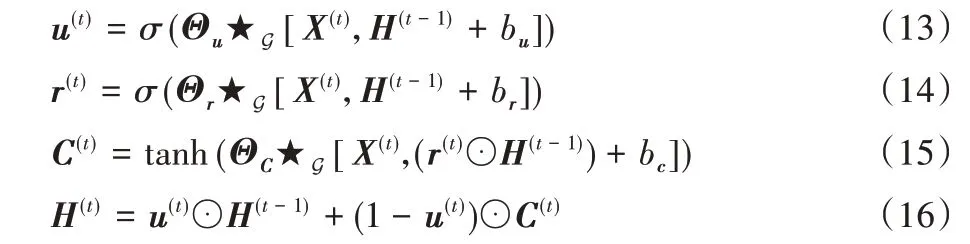
其中：★G为图卷积操作，X(t)为t时刻的输入，为可学习参数；H(t-1)为t-1 时刻的隐藏状态，当t=1 时，有H(t-1)=H(0)为初始的隐藏状态；ut、rt分别表示更新门和重置门；C(t)、H(t)分别表示t时刻候选隐藏状态和隐藏状态；σ为sigmoid 激励函数；⊙表示哈达玛积。

步骤2 将所有的循环单元串联，使每个循环单元的输出都作为下一个循环单元的隐层输入，所有串联的循环单元便组成一个图卷积门控层，图3 详细展示了图卷积门控层的组合过程。

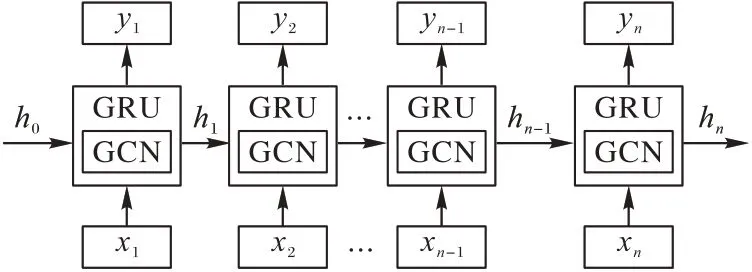
图3 图卷积门控层Fig.3 Graph convolutional gating layer

步骤3 叠加3 个图卷积门控层，并且图卷积门控层之间使用ReLU 激励函数连接，最后用一个全连接层输出预测结果。

3 实验设计与验证

为了验证模型的预测效果，本文在真实的数据集上对GCN-GRU 模型进行测试。本章将对数据集和实验设计进行说明，并对实验结果进行详细的对比分析。

3.1 数据集描述

采用中国气象数据网（http：//data.cma.cn/）提供的中国甘肃国家级地面气象站逐小时观测数据，该数据集包含了从2020 年8 月4 日0 时到2020 年9 月20 日23 时共48 d、74 个气象观测站的气象数据。因此实验数据主要包含两部分：一个是用于描述气象站点的地理位置数据，该数据用于构建邻接矩阵，主要包括区站编号、站名、经纬度、气压传感器海拔高度和观测场海拔高度；另一个是用于描述每个气象站点的天气状况数据，该数据用于构建特征矩阵，每隔一小时测一次，主要包括区站编号、日期、气压、风速、气温、能见度、云量和降水量等。

3.2 数据预处理

气象站点地理位置数据的预处理步骤如下：1）提取气象站点地理位置数据并删除异常站点；2）使用气象站点地理位置的经纬度数据，利用式（9）计算出每两个气象站点之间的距离；3）用高斯核函数将距离dij作为参数，计算出加权邻接矩阵。

气温数据的预处理步骤如下：1）根据气象站点地理位置数据预处理的结果，提取对应气象站点的气温数据；2）使用线性插值的方法填充缺失值和异常值；3）按滑动窗口的方式对气温数据进行时间切片；4）使用线性函数（Min-Max Scaling）方法对气温数据进行归一化。

3.3 实验设置

3.3.1 实验环境

实验环境如表1所示。

表1 实验环境Tab.1 Experimental environment

3.3.2 评价指标

本文选用3 个评价指标定量分析GCN-GRU 模型的性能，其中x(t)表示真实值，x^(t)表示预测值。

1）平均绝对误差（Mean Absolute Error，MAE）：

2）均方根误差（Root Mean Square Error，RMSE）：

3）平均绝对百分误差（Mean Absolute Percentage Error，MAPE）：

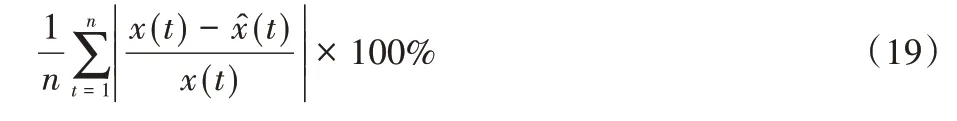
3.3.3 基线模型

为了测试GCN-GRU 模型的预测效果，本文与常见的气象预测领域的神经网络模型进行了比较，包括CNN、GRU、LSTM［10］和BLSTM-GRU；同时为了说明时间特征的重要性，与捕获空间特征的模型GCN 和ChebNet［16］进行比较；另外，与文献［15］的Cheb-LSTM（Chebyshev graph convolution and Long Short-Term Memory）、GCN-LSTM（Graph Convolutional Network and Long Short-Term Memory）等混合模型做实验对比。

3.3.4 参数设置

在实验中，将气温时序数据集以7∶3 的比例划分为训练集和测试集，模型输入的历史时间窗口为6 h，即H=6，预测未来6 h 的气温，即M=6。模型在进行多次调参的对比实验之后，最终确定的实验参数设置如下：三层图卷积门控层，每层使用的激励函数为ReLU；使用Adma 优化器和均方误差训练模型；训练轮次为100，批量大小为64，初始学习率为0.01。

3.4 实验结果与分析

3.4.1 寻找最优模型

为了得到最优预测结果的模型，1）本文将扩大图卷积感受野的参数K，使用了5个不同的值K=1，2，3，4，5，然后通过验证数据集观察预测结果，图4 展示了不同K值预测的效果。从图4 可观察到，随着K的增加，预测误差会较大幅度地减小，当K=3 时达到最小误差，然后缓慢地增加。2）对于重新分配邻接矩阵权重的参数p，选取了从0.01～1.00 共100 个值进行测试，图5 为参数p在不同值下的MAE 预测误差，可以发现随着p的增大，预测误差迅速减小，到达p=0.5左右时开始缓慢减小，一直到p=0.91时到达最小值，之后缓慢增加。

图4 不同阶数K下训练模型的MAEFig.4 MAE of training model under different orders K

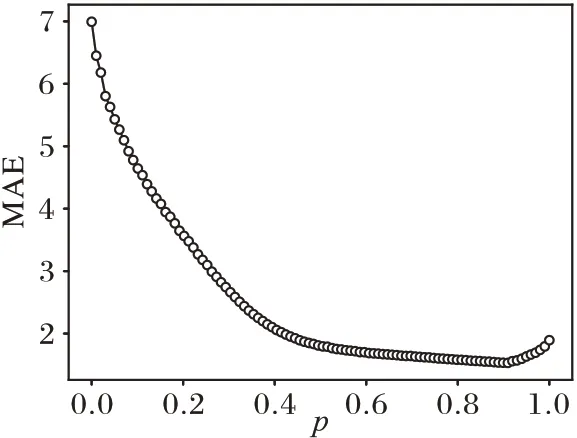
图5 参数p对模型预测结果的影响Fig.5 Influence of parameter p on model prediction results

因此本文确定模型中使用参数K=3，p=0.91，以达到最好的预测效果。

3.4.2 实验结果和分析讨论

观察表2 的实验结果可知：GCN-GRU 模型的MAE、MAPE、RMSE 均小于基线模型CNN、GRU、LSTM、BLSTMGRU、GCN 和ChebNet，其 中MAE 分别减小了1.54、0.67、0.83、0.25、0.72 和0.62；同时，GCN-GRU 模型的预测误差较Cheb-LSTM 和GCN-LSTM 模型也有明显地降低，其MAE 分别减小了0.36、0.23。

表2 不同模型的气温预测误差Tab.2 Temperature prediction error of different models

为了更直观地展示不同模型的预测效果，本文可视化了9 种模型在0 号气象观测站点的预测值与真实值。图6 为预测效果对比。由图6 可知，图6（a）展示的CNN 预测效果最差，图6（b）和（c）展示的循环神经网络模型比图6（d）和（e）模型效果好，但比图6（f）编码解码模型以及图6（g）和（h）组合模型效果差。图6（i）为本文的GCN-GRU 模型，相较于单一模型，预测效果具有明显的优势；相较于混合模型，随着预测时间步长的增加，预测效果的优势也更加明显，且能更有效地预测气温的最大值和最小值。

为了分析GCN-GRU 模型有更小预测误差的原因，本文可视化了测试集上每个气象观测站的MAE，点越大表示误差越大。如图7 所示，一个站点距离其他站点越远，此站点预测误差会随之增大，原因在于其他站点与此站点的空间相关性会随彼此之间距离的增大而减小，可见数据空间相关性是气温预测建模任务的关键因素。

图7 测试集上每个观测站的MAEFig.7 MAE of each observation station on testset

通过表3 比较GCN-GRU（No-modified）和GCN-GRU 预测误差可知，GCN-GRU 较GCN-GRU（No-modified）的MAE 减小了0.4，图6（i）展示了 预测结果，显 然GCN-GRU（Nomodified）对最高和最低气温的预测存在较大的误差，即预测结果过于平滑，可见使用本文方法改进的GCN 能够有效地捕获数据的空间相关性。综上所述，GCN-GRU 较传统方法有更小的预测误差。

表3 未修正图卷积的GCN-GRU与GCN-GRU气温预测误差结果Tab.3 Temperature prediction error results of GCN-GRU with graph convolution without modification and GCN-GRU

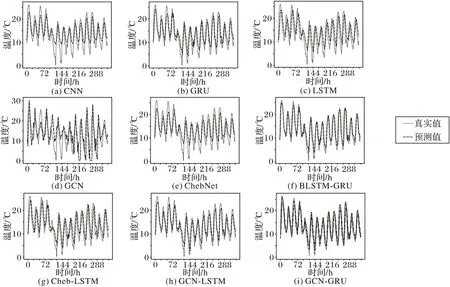
图6 不同模型的气温预测值与真实值Fig.6 Predicted and true temperature values of different models

4 结语

本文将一个地区的气象观测站建模成图网络，提出一种基于时空卷积的深度神经网络模型GCN-GRU 进行多站点气温预测。具体来说，将GRU 循环单元的矩阵乘法换成图卷积操作，捕获数据的时空关系。进一步地，将GCN 使用重新分配权重和多阶近邻连接的方法进行改进，以减小模型预测的误差。结果表明，与经典模型GRU、LSTM 等相比，GCNGRU 模型具有更小的预测误差。

本文只考虑了气温特征进行预测，在接下来的工作中，将融合其他气象特征，减小气温预测的误差。