变长度弹性伸缩腿双足机器人半被动起步行走仿人控制

张 瑞，张奇志，周亚丽

（北京信息科技大学自动化学院，北京 100192）

0 引言

步行是人类最常见的运动方式，如何使双足机器人实现像人一样稳定行走这一问题，引起了学者的广泛关注。双足行走机器人通常可以分为两类：其一是不使用被动动力学的全驱动行走机器人；其二是能量高效的被动行走机器人。

全驱动行走机器人通常采用反馈控制，例如采用轨迹跟踪控制的ASIMO 机器人［1］、混合零动力学控制的MABLE 机器人［2］，可使机器人在水平面和不平整的地面行走。采用这些控制方法的行走机器人，控制系统通常具有高增益、复杂庞大的特点，与人类行走相比能耗高、能效低。纯动行走机器人［3］可以在很小的斜坡上只依靠重力作用连续行走，行走过程中并不需要任何的控制和驱动，行走方式自然，但是此类行走方式稳定性差。半被动行走机器人［4-5］结合了全驱动行走和被动行走的优点，通过对部分关节施加驱动和控制，降低了系统能耗，提高了能源使用效率，可以充分利用自身动力学和自稳定特性抵抗部分扰动，行走更加自然，能够在水平面上连续行走。

为使机器人行走步态与人类更为相似，Geyer 等［6］提出了双足弹簧负载倒立摆（Bipedal Spring-Loaded Inverted Pendulum，B-SLIP）模型。弹簧负载倒立摆（Spring-Loaded Inverted Pendulum，SLIP）是一种可以代表人类质心运动轨迹的简化模型，同时可以生成与人类行走相似的地面反作用力模式。Garofalo 等［7］采用双足弹簧负载倒立摆模型提出了两级控制，实现了5 自由度机器人的周期行走步态。Rezazadeh 等［8］基于SLIP 模型在ATRIAS 机器人上实现了原地踏步和从静止起步加速行走进入稳定行走状态，同时还实现了步态之间的相互切换。Dazazadeh 等［9］基于SLIP 模型采用两级控制器实现了带有躯干的多体双足机器人的稳定行走。

目前半被动双足机器人行走控制研究的主要不足是：1）系统在给定的初始条件下开始运行，没有考虑机器人从静止阶段起步，由低速加速到稳定行走状态的过程；2）控制系统采用传统控制策略或基于深度学习［10］的控制方法，控制机器人按预先规划好的轨迹行走。

通过观察人类的行走方式发现：人类行走时大部分时间处于近似被动状态［11-12］，通过后腿蹬地改变系统的能量，并且促使人体重心前移，增加人体的前进速度；通过前腿触地位置控制人体重心高度和前向运动速度，防止向前倾倒。

根据上述研究，结合主动行走与被动行走的优点，本文提出了一种半被动起步行走仿人控制方法，在SLIP 模型基础上，采用串联弹性驱动B-SLIP 模型，利用拉格朗日方法得到行走动力学方程。在双支撑阶段，当系统状态离开稳定区域时，采用能量误差比例积分（Proportional-Integral，PI）反馈控制与惰性控制方法控制后腿伸缩，使系统总能量接近期望行走能量值并将系统带入稳定状态；在单支撑阶段，采用摆动腿回摆方法，通过改变摆动腿触地位置来控制机器人的高度和前向速度。此方法充分利用系统动力学原理，能量高效，且不需要跟踪期望轨迹。仿真实验结果表明，该策略可以实现机器人在水平面上的起步行走过程，并且控制系统具有抗干扰能力和鲁棒性。

1 双足机器人动力学模型

本文采用的系统模型来源于实验室自行研制的半被动双足行走机器人Sun Robot，如图1 所示。采用串联弹性驱动双足弹簧负载倒立摆（B-SLIP）模型作为简化模型［13］，如图2所示。

图1 双足机器人Sun RobotFig.1 Bipedal robot named Sun Robot

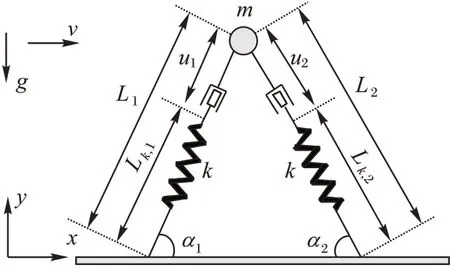
图2 双足机器人模型Fig.2 Model of bipedal robot

文献［13］中采用的机器人模型直接将后腿伸缩长度u1与前腿伸缩长度u2作为控制量，机器人样机腿部采用滚珠丝杠机构控制机器人行走时的腿长度。因此，本文在文献［13］机器人模型基础上，在机器人腿部引入理想化的电机驱动，通过控制机器人腿电机速度进而控制机器人行走时腿伸缩长度，同时对电机运行速度和腿伸缩长度进行了限制，更加符合实际情况。

该模型由一个髋关节和两条无质量的弹簧腿组成。假设机器人所有质量都集中在髋关节，忽略关节摩擦的影响，并且在行走过程中假定脚与地面没有相对滑动。前后腿原长为L0，后腿和前腿长度分别为L1和L2，后腿和前腿与地面所成角分别为α1和α2，弹簧刚度为k，后腿和前腿的伸缩长度控制量分别为u1和u2，髋关节质量为m，摆动腿触地角为α，且此时摆动腿长度为L0，重力加速度为g。

选择髋关节质心位置（x，y）为系统的广义坐标，采用拉格朗日方法可得串联弹性驱动双足弹簧负载倒立摆模型行走动力学方程，系统双支撑阶段动力学方程为：

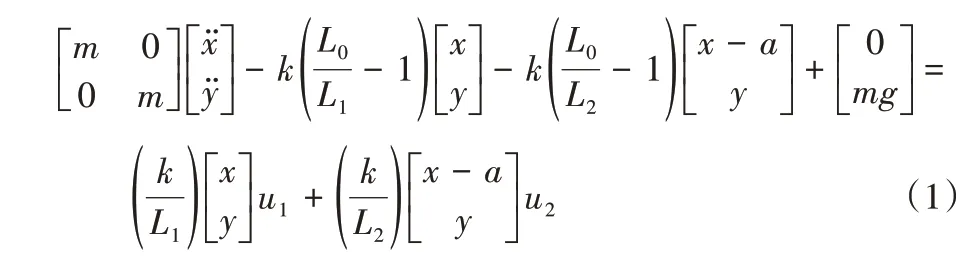
其中：为水平方向加速度，为竖直方向加速度，a为机器人行走时摆动腿触地点的x坐标值，u1和u2分别为后腿和前腿的伸缩长度控制量。

单支撑阶段动力学方程为：

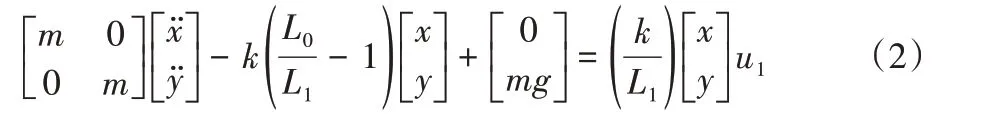
在向前行走过程中，机器人从双支撑切换到单支撑的切换条件为后腿L1达到原长，且脚的速度向上，即：

机器人从单支撑切换到双支撑的切换条件为髋关节高度到达H，且脚的速度向下，即：

2 起步行走仿人控制策略

2.1 双支撑阶段

传统行走控制利用近似解析解或数值近似解得到期望轨迹，采用轨迹跟踪控制方法实现双足机器人周期行走。为保证系统性能，一般闭环系统具有较高的刚度。即使没有外界干扰，由于近似解得到的期望轨迹与真实解存在误差，跟踪控制需要较大的控制力，能量效率不高。

文献［6，14］研究表明，采用无驱动的B-SLIP 模型，在系统具有特定能量的前提下，假设给定合适的初始条件，机器人能够实现稳定的纯被动行走，系统即使遇到小扰动，也可以利用自身的动力学特性调节系统回到稳定状态，即系统具有自稳定性，并且机器人在不同的能量下会表现出不同的运动状态。因此，可以利用模型的自稳定性，通过选取期望的周期行走能量值，设计控制器控制腿的伸缩，使系统总能量达到期望值，实现机器人的稳定行走过程。

2.1.1 主动控制

为使机器人从静止状态加速进入稳定行走阶段，模仿人类行走时后腿蹬地的行为，伸长后腿推动髋关节向前移动，增加行走时的前向加速度，进而增加系统的动能和总能量，最终使系统的总能量达到期望总能量值。

串联腿伸缩控制装置可采用滚珠丝杠系统实现，后腿控制装置的伸缩量u1可由式（5）表示：

其中v1(vmin＜v1＜vmax)为后腿伸缩控制装置的电机运行速度，对行走过程中的输入u1进行限制，即umin＜u1＜umax。在机器人腿与地面的接触过程中，弹簧由于机器人自身自重一直处于被压缩状态。定义伸缩装置电机速度v1为正值时，伸缩装置伸长，此时弹簧继续被压缩，系统总能量增加；当伸缩装置电机速度v1为负值时，伸缩装置缩短，此时弹簧被释放，系统总能量降低。因此，可以通过改变双足机器人的后腿长度来控制双足机器人的总能量。

机器人行走过程中的总能量E（t）为：

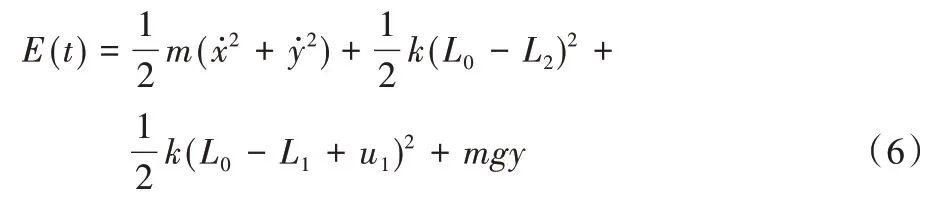
在只有后腿驱动器作用下，系统总能量随时间变化为：

其中：F=k(L0-L1+u1)为后腿弹簧弹力，v1为后腿驱动器电机速度。

对式（7）进行整理，则系统总能量导数为：

在机器人行走过程中，定义系统总能量与期望行走总能量Ed的误差e（t）为：

采用能量误差PI 反馈控制：

其中：KP＞0 为比例系数，KI＞0 为积分系数，对式（9）求导，结合式（10）可得：

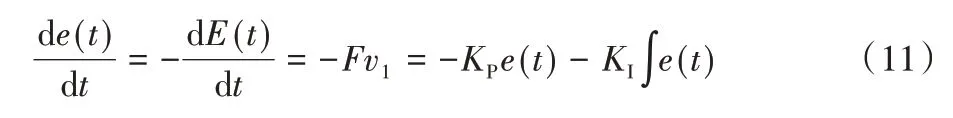
对式（11）求导得到系统的误差动力学方程：

由式（12）可知，系统总能量渐进稳定到期望总能量Ed。

对式（8）式（9）和式（10）进行整理，得到后腿驱动器的电机速度v1为：

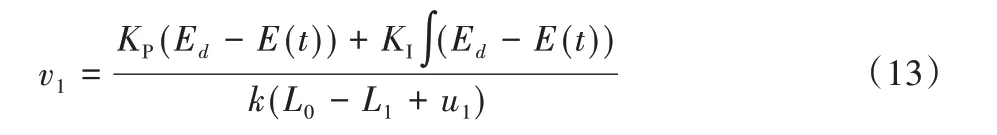
2.1.2 惰性控制

当系统的总能量到达期望总能量时，机器人仅依靠自身动力学特性进行纯被动行走；然而，在系统总能量接近期望总能量时，双足机器人就可以实现纯被动的连续稳定行走，因为此时机器人在每个行走周期的初始状态已经接近行走不动点。

为减少机器人行走时能量输入并提高行走鲁棒性，本文采用Suzuki 等［15-16］提出的惰性控制（lazy control）方法，将其应用到双足机器人在水平面的起步行走过程中，仅在系统状态离开稳定区域（在本文中，此处稳定区域只是不动点吸引域的一部分，并不是全部不动点吸引域）时才提供主动控制使系统保持稳定，使机器人的运动轨迹逐渐收敛到期望的周期行走轨迹。当系统状态进入稳定区域后，机器人可以依靠自身动力学特性实现零输入的被动稳定行走。

根据选取的期望周期行走不动点q*和进入双支撑阶段的初始状态q0，利用两状态向量间的欧氏距离作为偏差eq来判断进入当前步态的初始状态是否在稳定区域Q内，偏差eq如式（14）表示：

以不动点q*为原点，稳定区域Q的半径为δ，同时为了避免机器人的输入切换在稳定区域和不稳定区域的边界上引入噪声，定义参数0 ＜β＜1，将稳定区域Q分为内Qinner和外Qouter两部分，可由式（15）～（17）表示：

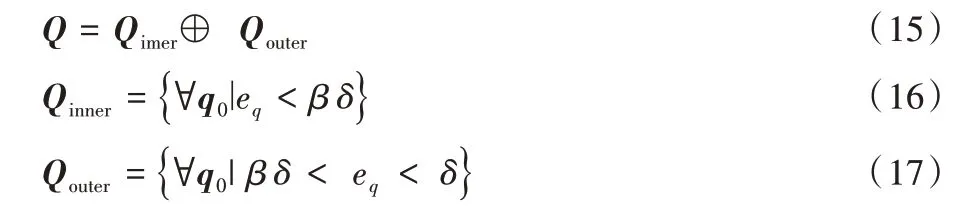
机器人在每个行走周期中的双支撑阶段的初始状态所在区域决定了控制系统是否进行主动控制，定义参数τ来表示这一结果。若初始状态q0在区域Q之外，即eq＞δ，τ为1，表示系统需要进行主动控制，采用能量误差PI 反馈控制为系统补充能量，使机器人的运动轨迹逐渐趋向于期望的行走轨迹；若初始状态q0在区域Qinner内，τ为0，表示系统不需要进行控制，机器人此时的状态已接近于不动点q*，机器人进行纯被动行走；若初始状态q0在区域Qouter内，τ则保持上一行走周期的值不变，表示现有的控制状态不变。式（18）表示了τ的取值与系统初始状态的关系：

根据式（13）和式（18），在双支撑阶段综合使用能量误差PI 反馈控制和惰性控制，得到机器人后腿驱动器的电机速度v1为：

2.2 单支撑阶段

一个完整的双足机器人行走周期包括双支撑和单支撑两个阶段，研究表明，在人类行走过程中，腿在单支撑阶段基本是被动的［12］。根据此项研究，在单支撑阶段仅通过控制摆动腿的摆动来实现机器人的稳定行走。

在单支撑阶段，摆动腿采用固定的触地角策略，机器人可以实现稳定的行走［6］和跳跃［17］，但是此策略并不能使机器人在低速行走或遇到外界扰动时连续行走。Seyfarth 等［18］提出了前馈摆动腿回摆策略，该策略模仿动物奔跑时向后摆腿的行为，而人类在行走时，摆动腿会表现出同样的行为。为提高机器人行走时（尤其是在低速行走时）的鲁棒性，本文也采取相似的策略。当摆动腿在空中摆动时，模仿人类行走时摆动腿回摆行为，机器人摆动腿的触地角度α（t）为：

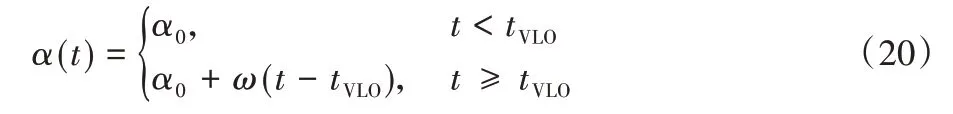
其中：α0为摆动腿的初始角度，ω为回摆角速度，tVLO为支撑腿位于竖直位置时的时间。

由于在单支撑阶段，只调节摆动腿的触地角度且忽略腿的质量，因此在单支撑阶段系统总能量恒定。当机器人前向速度过快时，触地角度变小（触地点靠前），弹性力的水平分量变大，机器人的前向速度降低；反之，当机器人前向速度过慢时，触地角度变大（触地点靠后），弹性力的水平分量减小，机器人的前向速度提高，从而稳定机器人的前向速度。

3 仿真分析

为验证起步行走仿人控制策略的有效性，在Matlab 中进行实验仿真，由于动力学方程具有非线性特性，采用4 阶龙格库塔法进行数值计算，仿真所使用参数来源或参考文献［7，16，19］：m=80 kg，g=9.81 m/s2，k=15 696 N/m，L0=1 m，u1∈［-0.05，0.05］m，v1∈［-0.5，0.5］m/s，α0=63.5 deg，ω=45.5 deg/s，KP=0.95，KI=2×10-7，β=0.5，δ=0.18，α1=α2=75 deg，前后腿点足之间距离为0.45 m，选取期望周期行走参数q*=［x；y；x′；y′］=［0；0.999；1.172；0］，计算得到期望行走能量为838.966 4 J。

3.1 干扰下的起步行走仿真分析

图3 为无干扰下系统总能量和速度随行走距离变化曲线。从图3 中可以看出，机器人在经过2 步（x=1.06 m）行走后，髋关节的水平速度为1 m/s（达到78%期望行走速度），可以在较短步数内提升行走速度，最终水平方向的最大行走速度稳定在1.27 m/s。对后腿驱动器所做功进行计算，无惰性控制的系统，后腿驱动器做功110.830 6 J；有惰性控制的系统，后腿驱动器做功107.919 7 J，在保证机器人能够稳定行走的前提下，采用惰性控制的系统减少了能量输入。

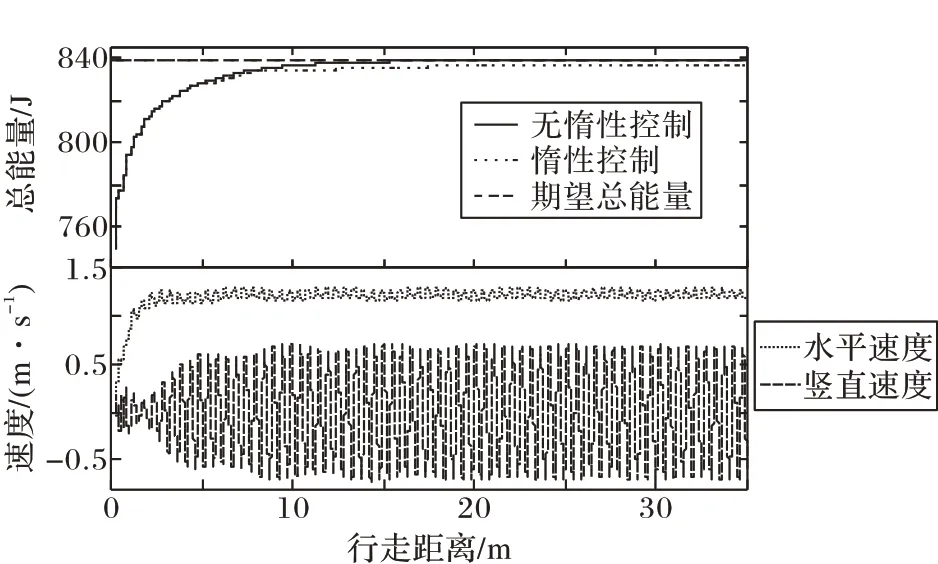
图3 无干扰下，总能量和速度随行走距离变化曲线Fig.3 Curves of total energy and speed varying with walking distance without disturbance

图4 为无干扰下系统初始状态偏差随行走距离变化曲线，随着机器人行走距离逐渐变大，初始状态偏差最终稳定在区域Qinner中，实现纯被动稳定行走。图5 为无干扰下τ值随行走距离的变化曲线：当τ=1 时，系统处于被控状态；当τ=0 时，系统处于纯被动行走状态。结合图4 和图5 进行分析，起步前机器人在原地处于静止状态，系统初始状态处在区域Q之外，需要主动控制将机器人带入稳定区域Qinner，τ=1，在机器人行走到7.707 m 之前，一直处于被控状态，持续为机器人补充能量；然后，机器人行走至7.707 m 之后，系统不再为机器人进行能量输入，仅通过单支撑阶段的摆动腿控制方法稳定纯被动机器人的状态，最终系统状态逐渐从区域Qouter过渡到区域Qinner内，此时机器人的运动轨迹接近于期望的行走轨迹。区域Qouter和Qinner大小与选取的参数β、δ相关，可以通过减小参数δ和β来减小区域Q和Qinner，使机器人最终被动行走时的状态与不动点更加接近，当参数δ和β均为零时，惰性控制便不再起作用，机器人总能量到达期望总能量，机器人状态与不动点重合，机器人运动轨迹与期望轨迹重合。

图4 无干扰下，系统初始状态偏差随行走距离变化曲线Fig.4 Curve of system initial state error varying with walking distance without disturbance

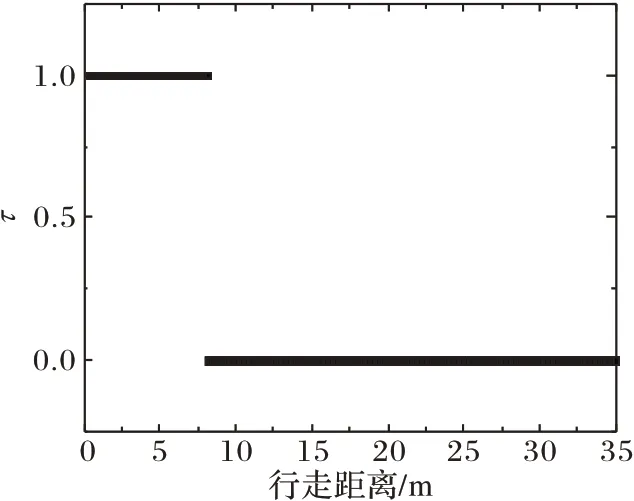
图5 无干扰下，τ值随行走距离变化曲线Fig.5 Curve of τ value varying with walking distance without disturbance

图6 为无干扰下髋关节高度和触地角随行走距离变化曲线。当系统总能量保持恒定后，通过改变触地角调节髋关节的高度和速度，最终触地角趋于恒定值。综上，仿真结果表明：起步行走仿人控制策略可以使机器人在水平面上完成起步行走过程，并且减少了系统的能量输入。

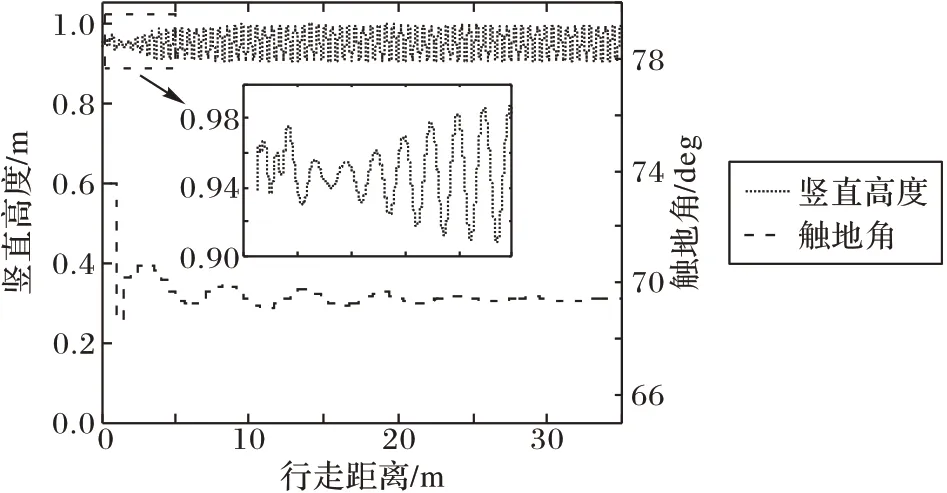
图6 无干扰下，髋关节高度和触地角随行走距离变化曲线Fig.6 Curves of hip joint height and touch-down angle varying with walking distance without disturbance

图7 为文献［13］中采用轨迹跟踪控制方法在无干扰同等条件下，机器人稳定行走阶段前后腿伸缩长度控制输入。可以看出，系统输入一直存在，这是由于在跟踪轨迹过程中误差总会存在，因此机器人系统需要一直消耗能量来跟踪期望轨迹。本文设计的间歇控制方法在机器人最终的稳定行走阶段不消耗能量，充分利用机器人被动行走原理和双支撑阶段自稳定特性，与文献［13］的控制方法相比，能量效率更高。

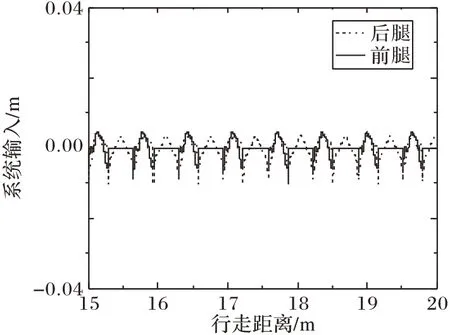
图7 文献［13］中机器人稳定行走阶段的系统输入Fig.7 System input of robot in stable walking stage in reference［13］

3.2 外部扰动力下的起步行走仿真分析

为考察系统对干扰的鲁棒性，在机器人起步行走过程中持续施加外部周期扰动，扰动力F1=(-FxcosΩ t；FysinΩ t)N，其中Fx为水平方向上的扰动幅值，Fy为竖直方向上的扰动幅值，Ω为扰动频率，t为行走时间。数值仿真时，水平方向上的扰动幅值Fx为15 N，竖直方向上的扰动幅值Fy为30 N，扰动频率Ω为12 Hz，其余仿真参数仍与3.1 节相同。

图8 为干扰下系统总能量和后腿驱动器输入随行走距离变化曲线。从图8 中可知，机器人在存在周期外部扰动力的情况下，前期通过控制输入为机器人补充能量，机器人的总能量逐渐增加，当机器人接近期望总能量后，不再有控制输入，机器人纯被动行走至11.713 m 处后，机器人有短暂的能量补充，而后机器人一直保持纯被动行走状态。即使始终存在外部扰动力，机器人仍然可以通过自身的调节，利用动力学特性，最终实现连续纯被动稳定行走。

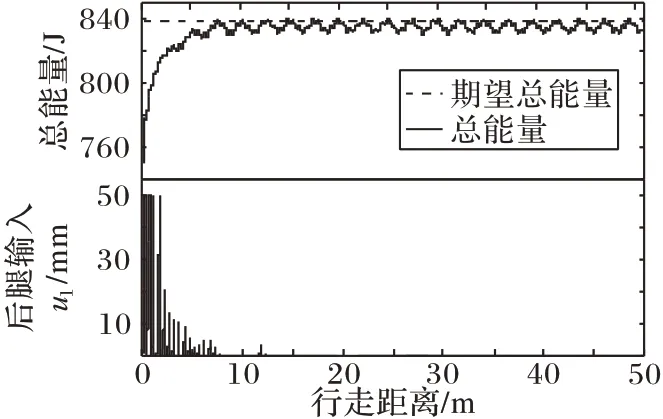
图8 干扰下，总能量和输入随行走距离变化曲线Fig.8 Curves of total energy and input varying with walking distance with disturbance

图9 为干扰下机器人初始状态偏差随行走距离变化曲线。前期通过控制作用使机器人状态逐渐进入稳定区域Q，虽然外部扰动力一直存在，但是经过摆动腿逐渐调节触地角，系统的初始状态最终稳定在区域Q中，期间没有能量输入，一直保持纯被动行走状态。当机器人遇到外界扰动偏离期望运动轨迹后，从文献［13］中可以看出，轨迹跟踪控制方法需要通过控制作用使机器人逐渐回到期望运动轨迹上，本文采用的控制方法可使机器人遭受到外界扰动后并不需要控制输入，利用自身动力学特性，在节省系统能量和抵抗外界扰动上具有一定的优势。综上，仿真结果表明：控制系统对于持续的周期外部扰动力具有抗干扰能力，可以实现在水平面上的起步行走过程。

图9 干扰下，初始状态偏差随行走距离变化曲线Fig.9 Curve of initial state error varying with walking distance with disturbance

4 结语

本文采用串联弹性驱动双足弹簧负载倒立摆模型，结合主动控制与被动行走的优点，提出了一种半被动双足机器人起步行走仿人控制方法。该方法模仿人类行走，通过伸长后腿为系统注入能量，采用摆动腿回摆方法控制触地位置。仿真结果表明：起步行走仿人控制策略可以实现变长度弹性伸缩腿半被动双足机器人在水平面上起步行走，减少了能量输入，控制系统对外部扰动力具有抗干扰能力。

本文与已有的研究主要在两方面存在不同：1）在串联弹性驱动双足弹簧负载倒立摆模型基础上提出了完整的起步行走仿人策略，实现了仿人的起步行走过程；2）相较于传统轨迹跟踪控制方法，本文提出的主动与被动相结合的控制方法不需要跟踪轨迹，充分利用了被动行走的自稳定性与周期性，利用系统动力学原理减少能量输入，能量效率高。在本文理论研究和仿真实验的基础上进行硬件平台的验证是下一步的工作方向。