基于动态网络的非线性置乱扩散同步图像加密

郭 媛，王学文，王 充，姜津霖

（齐齐哈尔大学计算机与控制工程学院，黑龙江齐齐哈尔 161006）

0 引言

随着移动网络的迅速发展，多媒体数字信息随之快速增加。数字图像作为一种主流的多媒体格式，其安全、快速传输成为信息安全研究热点。图像具有容量大、冗余度高、相邻像素间相关性强等固有特征，传统的文本数据加密算法无法满足其加密要求［1］。因此，许多基于图像特征的加密算法被提出，更加适应图像安全传输要求［2-3］。

混沌与密码学存在着许多相似处。因此，混沌被广泛应用于图像加密，而许多基于混沌的图像加密被证明存在安全问题。文献［4］中提出了一种三维矩阵置换机制，使每位都能移动到任意位置，得到置乱后位矩阵；但加密过程与明文无关，不同图像置乱与扩散的密钥流相同。Xie 等［5］利用数学语言分析，并且总结出此类加密算法的主要性质，表明明文无关算法密明文存在对应关系，可被选择明密文攻击破解［5-6］。为解决此类问题，明文相关算法被提出。Wang 等［7］提出一种基于比特级排列和脱氧核糖核酸（Deoxyribo Nucleic Acid，DNA）编码的图像加密算法，其中利用明文与混沌系统产生序列。Huang 等［8］对Arnold 映射进行扩展，并提出一种新型加密算法，算法中置乱与扩散操作都与明文相关。Wang 等［9］提出了一种并行的快速图像加密算法，扩散过程与明文相关，同时可并行加密，降低算法的时间复杂度。Norouzi 等［10］提出一种基于超混沌系统的单轮扩散加密算法，利用定位的像素总和作为明文特征值。谢国波等［11］先对明文进行像素位置置乱，再将其二值化交叉嵌入另外两组混沌序列，最后对两组混沌序列进行异或运算。Liu 等［12］提出一种块大小可变的图像加密算法。该算法先利用Arnold变换进行整体置乱，然后依据Baker 映射进行分块，最后利用像素和对分块进行加密。但有些明文相关算法也会存在安全问题。Diab 等［13］分析了文献［10］中所提算法，并运用选择明文攻击成功破解，同时获取密钥流可以在没有密钥的情况下解密其他明文的密文图。朱淑芹等［14］利用特殊图像可还原文献［11］算法的置乱图像，并通过多幅特殊图像成功破解。Ma 等［15］对文献［12］算法进行深入分析发现混沌序列生成与明文像素的平均值密切相关，先使用选择明文攻击获取扩散等价密钥，再利用特殊图像获取置乱等价密钥，其等价密钥可解密其他使用相同密钥加密的图像。上述被破解的明文相关算法存在置乱扩散分开独立操作问题。当明文图像为特殊图像时，加密算法安全性仅依靠扩散操作，一旦扩散被破解，明文统计信息将会暴露。因此，有些研究学者提出了置乱扩散同步算法。Enayatifar 等［16］提出一种基于DNA的同时置乱与扩散加密算法，在利用混沌序列获取新位置的时候，利用DNA 序列和DNA 算法进行像素扩散。Huang等［17］提出一种对称彩色图像加密算法，将彩色图像转为三维矩阵，通过混沌映射获得置乱位置，同步进行明文相关的扩散操作。但上述置乱与扩散同步算法存在扩散置乱非线性较低，扩散按照固有顺序进行，不同明文扩散前后置乱位置信息不变，易造成扩散与置乱信息暴露。Chen 等［18］指出若扩散按照固定顺序操作且利用前密文值来增加雪崩效应，则攻击者可以通过扩散顺序获知扩散解码方程中变量，简化扩散方程，方便攻击，并进行了严格分析，建议将非线性扩散引入图像加密中。Chen 等［19］利用加密不同明文置乱相对位置不变的特性提出一种通用破解算法，同时也建议在置乱中加入非线性。

针对上述问题，本文提出一种强非线性的置乱扩散同步加密算法。该算法具有以下优点：1）构造新型sine-cos 混沌映射，拓宽控制参数范围，改善序列分布和随机性，更适用于加密；2）明文像素和混沌映射的结合使不同明文的密钥流与像素网络结构不同，同时网络值动态更新，使网络动态改变，达到一图一密效果；3）用相邻节点像素和进行扩散，使扩散过程具有动态性，增加算法明文相关性，而且单像素扩散与置乱交替进行，无法分离置乱与扩散，使置乱扩散同步；4）依据网络结构转移像素操作，造成加密路径呈现网络结构，具有强非线性，使攻击者无法依据明（密）文获知扩散顺序以及置乱顺序。

1 基本原理

1.1 新型混沌系统

sine 混沌映射和kent 混沌映射结构简单易于实现，广泛应用于图像加密。sine 和kent 混沌映射分别为：

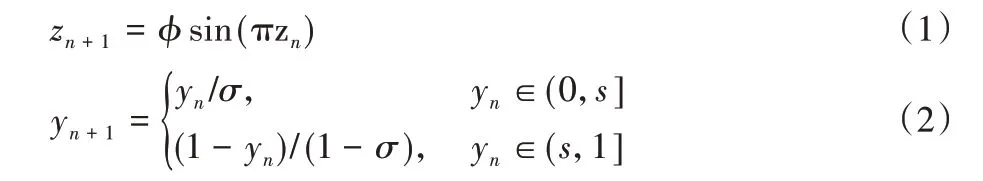
其中：参数φ∈(0.87，1)，σ∈(0，1)，序列z∈(0，1)，y∈(0，1)。

为克服sine 映射密钥空间小、稳定区窄与空白区等缺陷，对sine 进行改造得到新的混沌系统sine-cos。sine-cos 混沌映射为：

sine 混沌映射和sine-cos 混沌映射的分叉与lyapunov 指数如图1。如图1 所示，sine-cos 混沌映射参数μ范围比sine映射宽，达到整个正数集，混沌区中不存在空白区，同时lyapunov 指数稳定，更加适用于图像加密。

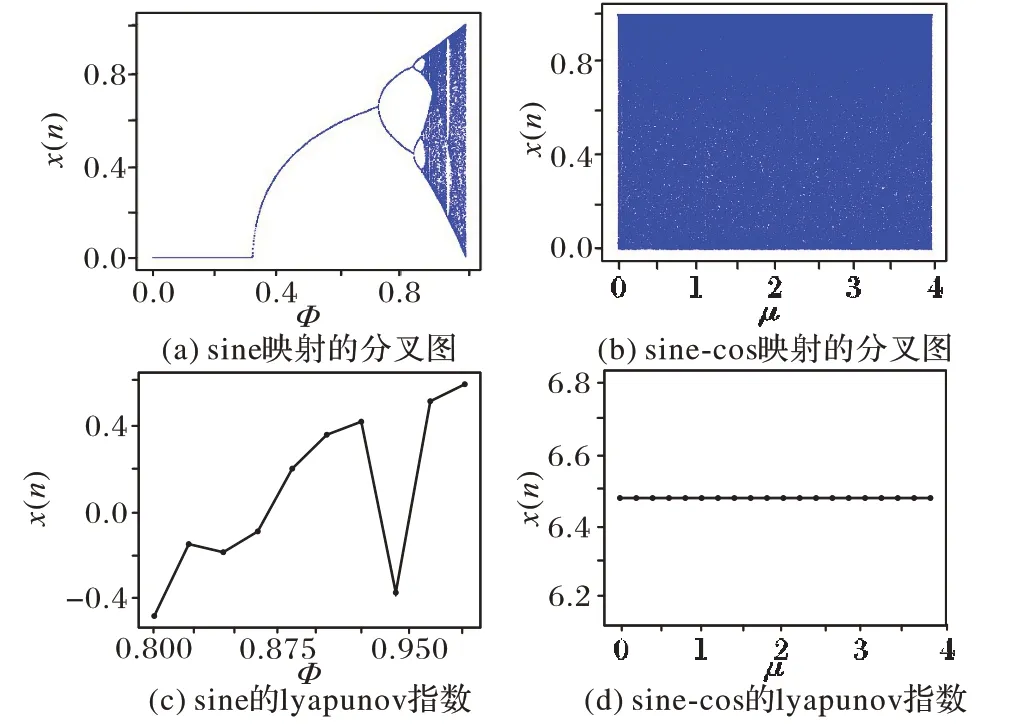
图1 sine混沌映射与sine-cos混沌映射的分叉图及lyapunov指数图Fig.1 Bifurcation of sine chaotic mapping and sine-cos chaotic mapping and lyapunov exponential map

1.2 动态网络

先用明文像素与混沌序列的异或和作为混沌初始值产生新混沌序列，再使用新混沌序列产生位置索引，最后利用位置索引连接不同位置像素产生不同像素网络，网络构建示意图如图2 所示。

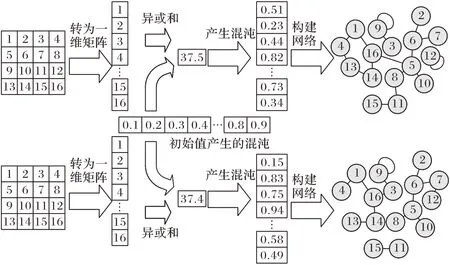
图2 不同明文的网络构建示意图Fig.2 Schematic diagram of different plaintext network construction

由于明文与混沌的异或是对应位置进行运算，最终异或和不仅与明文像素值有关，而且还与像素分布有关。即使直方图及像素和相同的明文图像，只需像素分布不同，其与混沌的异或和也不同。基于此不同明文必然产生不同的网络结构，使网络具有明文动态性。同时在置乱扩散阶段引进网络值更新机制，使算法在不同加密时刻网络也不同，进一步提高网络动态性，置乱扩散同步示意图如图3 所示。

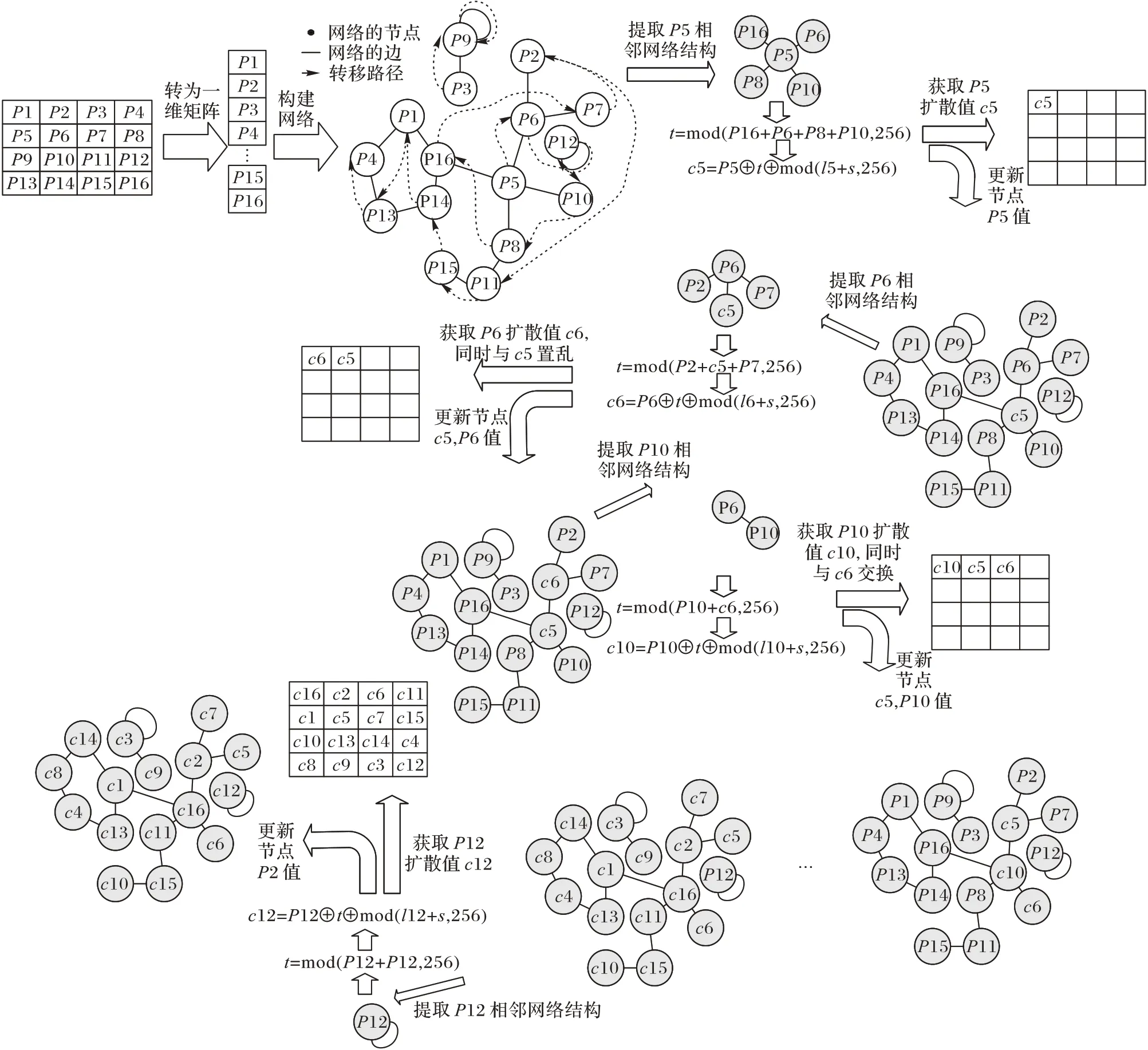
图3 非线性置乱与扩散同步示意图Fig.3 Schematic diagram of nonlinear scrambling and diffusion synchronization

1.3 非线性置乱扩散同步原理

现有加密算法其扩散方程大多采用式（4）的推广式，同时扩散过程按照像素一个一个被扩散（一般按照从第一个（左上）到最后一个（右下）依次扩散），最后将其放回原明文像素位置。运用微分思想（如式（5））可使扩散解码方程退化成只有混沌值的简单方程，进而使扩散变成图像与混沌矩阵对应位置像素异或的形式，攻击者则可通过构造不同特殊图像获取混沌值（扩散等价密钥）。而且前后相对位置未发生变化，造成置乱过程所产生的位置映射关系得到保留，存在经密文获取与置乱相关等价密钥的安全问题。

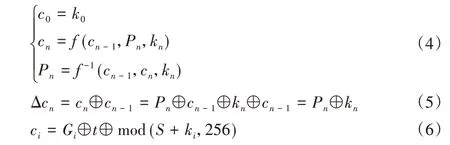
其中：cn和cn-1为当前密文像素和前密文像素；Pn为当前像素；kn为混沌值；f为加密函数，其为一些基本的非线性函数，如异或、模等；f-1为f函数的逆过程；S为像素异或和。

为提高算法非线性，将非线性网络结构作为像素操作转移依据，提出一种非线性置乱扩散同步算法。该算法先利用明文构建像素网络，再从网络中随机获取节点进行扩散及与源节点交换的操作，然后依据网络结构获取未扩散相邻节点进行相同操作。图3 为4×4 图像的非线性同时扩散与置乱示意图。

本文采用的扩散方程如式（6），依照动态网络结构转移扩散操作，使用当前扩散像素（Gi）具有随机性，同时前密文像素（ci）用相邻节点像素和t进行替代，网络更新使网络节点的相邻像素和动态改变，使前密文值具有动态性、随机性，扩散过程整体呈现非线性网络结构。扩散方程中各变量具有随机性，使攻击者无法确定式（5）中密文cn对应的cn-1，进而无法获知Δcn，使式（5）无效，导致现有扩散破解方法无效。与相邻源节点交换使密文像素在局部网络中调整，造成最终置乱依据网络结构，具有非线性。同时置乱和扩散交叉操作，造成置乱扩散整体无法分开达到置乱扩散同步的结果，也使置乱值动态变化。

2 加解密系统

明文图像P为一幅n×m的256 级灰度图，加密算法公共密钥为σ、μ、μ′、x0、y0。加密过程包括像素网络构建和单像素串行置乱与扩散，具体加密过程如图4 所示。解密公共密钥为σ、μ、μ′、x0、y0、S，S为异或和。

图4 加密过程Fig.4 Encryption process

2.1 加密系统

2.1.1 构建像素网络

2.1.2 单像素串行置乱与扩散

步骤4 利用式（14）对Gi进行扩散得到Ci。

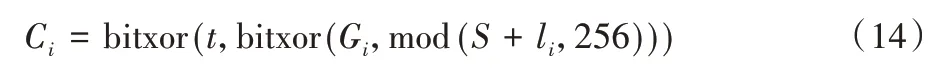
步骤5 步骤4 得到Ci与相邻来源节点C源进行交换。并用Ci、C源更新Gi、G源。若Gi为某连通图的第一个遍历点则不进行交换和更新。

步骤6 节点Ci、Gi作为C源、G源。判断Gi是否有未进行置乱与扩散的相邻节点：有则随机获取Gi的相邻节点Gi+1；没有则判断Gi的连通图是否有未处理节点。若有未处理节点，则获取离Gi最近的节点Gi+1；否则判断网络中是否具有未处理节点，随机获取节点Gi+1，对节点Gi+1进行步骤3～5的操作，最终得到中间密文C。

步骤7 将C转换为m×n密文矩阵C′。

2.2 解密算法

步骤1 利用混沌序列和密文产生网络G，对网络G进行广度优先遍历得到访问顺序L。按照L倒序进行像素节点还原。

步骤2 节点与访问来源节点进行交换，若为连通图的最后一个像素则不交换。

步骤3 计算节点相邻像素和，并将其转为0～255 的值，再利用式（15）进行扩散。

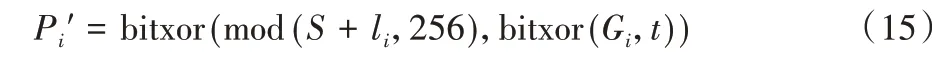
步骤4 不断执行步骤2～3，直到无未处理像素，最终得到P′。

步骤5 将P′转为二维明文矩阵P。

3 实验结果与安全分析

为验证算法的安全性和有效性，选择512×512 标准灰度图作为实验对象。公共密钥设为σ=0.599 99，μ=3.999 4，μ′=3.888 4，x0=0.237 5，y0=0.373 4。该算法加解密效果如图5所示，其密文呈为类噪声，明文所有信息被隐藏。解密图像与明文图像相同。

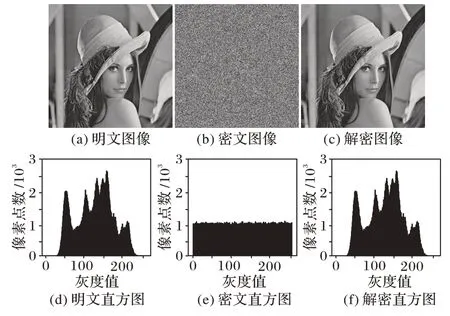
图5 加解密效果及对应的直方图Fig.5 Effects of encryption and decryption and corresponding histograms

3.1 统计特性分析

3.1.1 直方图

图像像素分布情况可用直方图进行描述。抗统计攻击的加密算法，其像素值分布均匀，相应的直方图分布也均匀。如图5 所示，密文直方图分布均匀，且与明文直方图有显著差异。因此，密文像素分布均匀，攻击者无法从密文图像中获取明文统计信息，能够抵抗统计攻击。

3.1.2 相邻像素相关性

明文图像中相邻像素一般具有强相关性。安全的加密算法应能打破强相关性，使密文相邻像素无相关性。同时相邻像素相关系数r可定量描述相邻像素的相关性。为形象化展示相关性，分别随机地在明密文水平（H）、垂直（V）和对角（D）3 个方向选取4 000 对相邻像素获得相关分布，如图6所示。

图6 相邻像素的相关性Fig.6 Correlation of adjacent pixels

明文图像相邻像素对呈对角线分布，密文均匀分布于平面，明文像素间具有高相关性，而密文像素间相关性并不高。明密文的相关性系数如表1 所示。明文相关系数比较接近1，而密文相关系数接近0，在Set14 数据集中平均相关系数也具有相同特性，进一步验证了密文相邻像素相关性低。

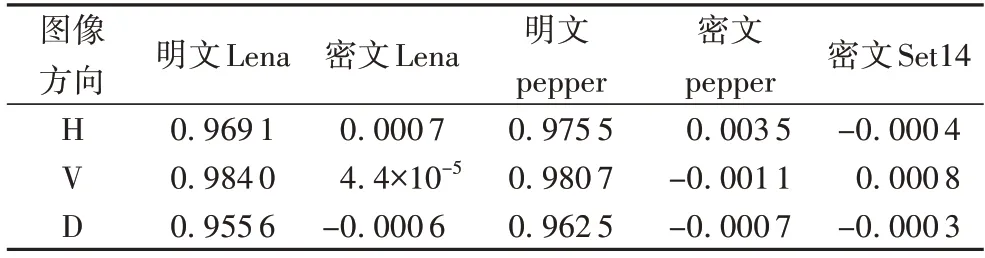
表1 密文图像像素相关系数Tab.1 Pixel correlation coefficient of ciphertext image

3.1.3 信息熵

信息熵反映图像像素的不确定性和随机性，信息熵值越大，随机性越强。信息熵计算公式如式（16）：

其中p(xi)∈(0，1)，p(xi)和等于1。

若256 灰度级的图像像素分布均匀，则信息熵接近理论最大值8。明文和密文的信息熵如表2 所示。

表2 信息熵Tab.2 Information entropy

其密文信息熵接近理论最大值8，在Set14 数据集中平均信息熵也接近8，表明该密文具有更强不确定性和随机性。

3.2 差分分析

3.2.1 明文敏感性分析

像素改变率（Number of Pixel Change Rate，NPCR）和统一平均改变强度（Unified Average Changing Intensity，UACI）可定量评价两幅图像差异。NPCR 值越大，意味着加密算法对原始图像的变化越敏感；UACI 值越大，图像平均变化强度越大。NPCR 和UACI 的定义如下：

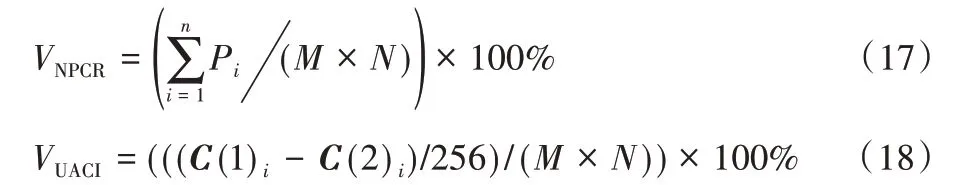
其中C(1)、C(2)为密文图像。当C(1)i=C(2)i时Pi=0，否则Pi=1。

本文采用图像随机一个像素加1 和随机交换两像素点的密文与图像的密文的NPCR 值和UACI 值来分析算法明文敏感性，结果如表3。两种改变方式NPCR 都达到99.6%以及UACI 都达到33.4%，表明任意改变方式，密文基本上所有像素值发生变化，具有强明文敏感性。

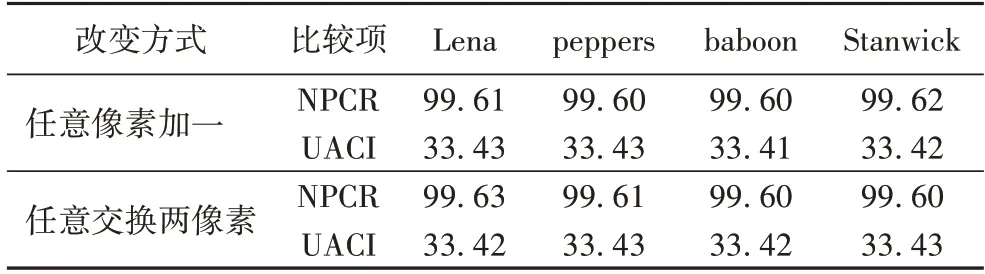
表3 NPCR和UACI值 单位：%Tab.3 NPCR and UACI values unit：%

3.2.2 密钥敏感性分析

安全的加密算法对密钥细微变化非常敏感，具有微小差别的密钥解密效果也不同。解密密钥发生微小变化时，其解密效果如图7 所示。

从图7 中可知，当密钥μ、x0相差10-16时无法还原明文图像，当密钥μ、x0相差10-17时可还原明文图像，故μ、x0的敏感度为10-16。同理σ、y0、μ′敏感度为10-16。由此可见该算法具有强密钥敏感性。

图7 密钥偏差时的解密图像Fig.7 Decrypted image with key deviation

3.3 密钥空间分析

本文算法的混沌系统参数分别为σ、σ′、μ、x0、y0，且参数采用具有16 位有效位的双精度数据。本文算法还将明文异或和S作为密钥，进一步扩大密钥空间。因此，算法的密钥空间至少为1096。本文算法具有足够的安全级别来抵抗穷举攻击。

3.4 抗攻击实验

作为评价加密算法安全性的抗攻击能力是密码分析重要步骤，本节采用特殊图像实验分析、一图一密分析、分步攻击分析和非线性性能分析来验证所提算法的抗攻击能力。

3.4.1 特殊图像实验分析

一些图像密码分析中通过构建特殊的图像（全黑或全白）来获取加密算法的破解信息。本文选择全黑、全白图像作为算法的测试对象，结果如图8 和表4。

表4 特殊图像的加密结果Tab.4 Encryption results of special images

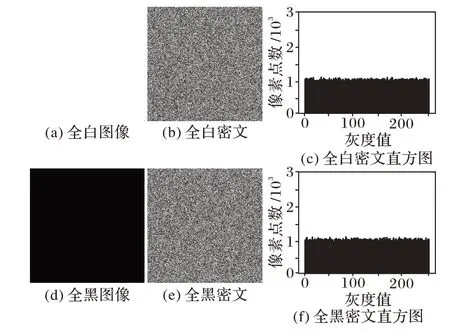
图8 特殊图像的实验结果Fig.8 Experimental results of special images

从8 和表4 中可知，低相邻像素相关性、均匀的直方图和密文呈类噪声，表明特殊图像的密文中无明显统计信息及其他信息；网络值更新和动态扩散，可增强扩散雪崩效应。同时本文利用异或和来与明文相关联，没有直接使用明文信息，不存在特殊位置，可以有效抵御特殊图像分析。

3.4.2 一图一密分析

获取图像加密时产生的混沌序列，将图像某位像素值加1 作为伪明文1，再取一张不同的图像作为伪明文2，分别对两张图像进行加密。用获取的混沌序列进行解密，其结果如图9。

图9 一图一密分析结果Fig.9 One image one key analysis results

伪明文1 与图像只有一个像素不同，但是无法使用中间密钥还原任何明文信息。而与之相差甚远的伪明文2 更无法还原明文信息。本文使用明文像素与混沌序列的异或和作为混沌初始值以及扩散混淆值，即使具有相同混沌序列，只要明文图像不同，产生的初始值和混淆值也会不同，使不同明文具有不同中间密钥以及像素网络结构。攻击者无法通过获取其他明文中间密钥来破解加密算法，达到一图一密效果。

3.4.3 分步攻击分析

为验证本文算法抵御分步攻击能力，采用Ma 等［15］所提分步破解方法作为测试方法，对本文算法与Liu 算法［12］进行对比。如图10 所示，两算法分别对Lena 图像（a）（e）进行加密得到密文（b）（f）。利用测试方法破解扩散得到中间图像（c）（g），最后构建特殊图像来得到解密图像（d）（h）；同时给出Lena 和（c）（g）的直方图。分布攻击结果如图10 所示。

从图10 中可知，Liu 算法［12］的中间图像直方图与明文图像的直方图相似，说明Ma 等［15］所提选择明文攻击可以破解Liu 的扩散算法［12］，恢复明文直方图信息；而本文的中间图像直方图与明文图像直方图完全不同，说明Ma 等［15］所提方法无法恢复明文直方图信息。这是因为单像素置乱扩散串行操作使置乱扩散整体同步，无法分离，使Ma 等［15］为扩散所设定的选择明文攻击无效，致使整个破解算法无效。本文算法可以较好地抵御分步破解的破解方法。

图10 分步攻击结果Fig.10 Step-by-step attack results

3.4.4 非线性性能分析

为验证本文所提算法非线性的安全性，采用Chen 等［19］提出的微分方程破解方法作为测试方法，如式（19），并与文献［20］算法进行对比。

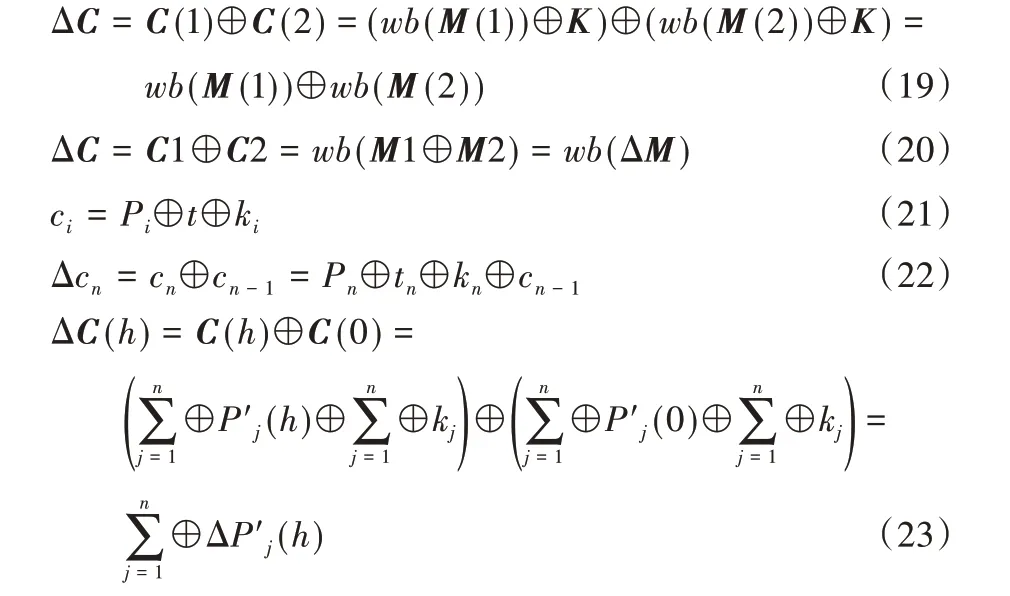
其中：ci为前密文像素，Pi为明文像素，Ci为密文图像，M(i)为明文图像，wb为置乱操作，k为混沌值，C(i)为密文图像，ΔC(h)为异或图像。

如图11 所示，两算法分别对Lena 图像进行加密，再利用所选攻击方法进行破解，得到密文恢复图像。结果表明，Chen 等［19］的破解方法可以恢复文献［20］算法的加密密文，而不能恢复本文算法的密文，表明本文算法可抵御文献［19］中所提的破解方法。Chen 等［19］所提方法利用了加密不同明文置乱相对位置不变的特性，但本文置乱位置信息依靠网络结构进行局部调整，由一图一密分析结果可知不同明文的网络结构不同，因此式（20）不成立可以抵御文献［19］中破解方法。同时，本文算法也可以抵御文献［18］中破解方法。在文献［18］中利用式（5）简化扩散方程以及运用级联微分（式（23））去除混沌序列。本文所用扩散方程可以简化为式（21），再对式（21）进行微分分析，如式（22），由于无法依据明密文对获知参数t，难以将式（22）转为式（5），无法进行后续级联微分分析。即使获知参数t，在未知扩散顺序时（即未知式（5）中cn对应的cn-1），无法产生微分对，使普通微分分析无效。综上所述，由于本文算法依托网络结构进行置乱扩散，使算法具有强非线性，可抵御现有破解方法的分析。

图11 攻击测试结果Fig.11 Attack test results

3.5 加密时间分析

作为评价算法高效性的指标，其加密时间越低算法越高效。本文算法的主要时间花费在提取网络节点上，由于本文使用邻接表存储方式，顶点个数为明文像素个数，边的个数为明文像素个数的2 倍，故算法时间复杂度为O(3×n×m)，与图像大小成正比。表5 为在不同大小图像的加密时间。

从表5 可知，本文算法加密时间较低，且与图像大小成正比，具有一定的高效性。

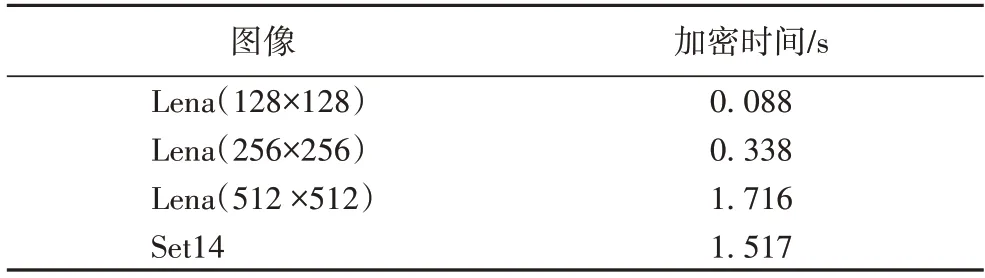
表5 加密时间Tab.5 Encryption time

3.6 对比分析

为衡量本文算法性能，将从熵、相关系数、NPCR 和UCAI等方面与文献［16，18］算法进行比较，结果如表6。

从表6 可知，本文所有指标都优于文献［16，18］的算法，整体上具有良好性能。

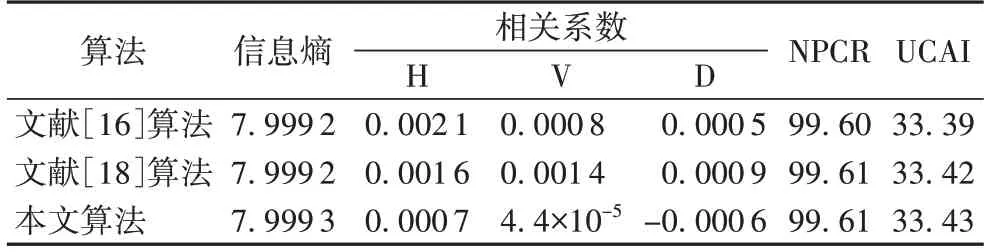
表6 不同算法性能结果比较Tab.6 Performance results comparison of different algorithms

3.7 非线性分析

为度量所提算法非线性程度，利用式（24）计算不同大小图像加密过程产生网络的非线性度Nol，结果如表7。

其中：i为网络中节点的度，Ω为网络中不同节点度的集合空间，P(i)为网络中节点度为i的概率。

从表7 中可知，本文算法在不同图像大小下非线性度都在5.4 左右，比文献［16，18］的算法大1.4。本文所提算法具有高非线性。

表7 不同大小图像的非线性程度Tab.7 Nonlinear degree of different size images

4 结语

本文提出了一种具有动态非线性加密过程、抗攻击性能优的高安全图像加密算法。该算法设计sine-cos 混沌映射克服了sine 混沌映射稳定区窄、存在空白区等缺陷，增加分布随机性，更加适应图像加密。混沌映射初始值由明文像素与混沌序列的异或和产生，使算法具有一图一密性。混沌与明文像素产生像素网络，网络值更新机制使网络动态改变。单像素交替置乱扩散以及依据网络结构转移像素操作，使置乱扩散同步的同时路径呈网络结构，使算法具有强非线性，可抵御现有破解方法。基于相邻节点像素和的动态扩散，增强明文相关。实验结果表明，该算法加密效果好，无明显统计特征，具有强明文相关性和抗攻击能力。