优化搜索空间下带约束的可微分神经网络架构搜索

李建明，陈 斌，江志伟，覃 健

（1.中国科学院成都计算机应用研究所，成都 610041；2.中国科学院大学，北京 100049；3.哈尔滨工业大学（深圳）国际人工智能研究院，广东深圳 518055；4.中科院广州电子技术有限公司，广州 510070）

0 引言

网络架构是影响卷积神经网络（Convolutional Neural Network，CNN）的重要因素，有些学者致力于改进神经网络架构的设计以提升其性能［1-5］。其中，比较有代表性的网络架构有：谷歌网络（GoogLenet）［2］、残差网络（Residual Network，ResNet）［3］、稠密卷积神经网络（Dense convolutional Network，DenseNet）［4］、压缩激活网络（Squeeze-and-Excitation Network，SENet）［5］等。虽然这些网络架构在ImageNet 数据集上的表现逐年得到了提升，但其设计过程由专家手动实现，需要专家耗费大量时间进行试错实验，所以这种方法效率较低。自神经网络架构搜索（Neural Architecture Search，NAS）［6］被提出以来，越来越多的研究开始采用此类方法，模拟人类专家自动设计网络架构，以提升设计的效率和架构的性能。

按NAS 采用的优化方法，目前常用的方法大致可分为三类：基于强化学习（Reinforcement Learning，RL）［6-7］的搜索方法、基于进化算法（Evolutionary Algorithm，EA）［8-9］的搜索方法和基于可微分架构搜索（Differentiable ARchiTecture Search，DARTS）方法［10］。其中，DARTS 方法在超网络端到端的训练中，以基于梯度（gradient-based）的优化方式实现了架构搜索，具有计算资源需求较低、搜索效率高的优点［10］。该方法引起了众多学者的关注，并出现了一系列的改进方法［11-16］。文献［11］提出了一种新的可微分神经网络架构搜索（Differentiable Neural Architecture Search，DNAS）框架，通过逐层构建可搜索模块的方式重新设计搜索空间，并引入耿贝尔（Gumbel）采样建模搜索过程，以得到精度和运算效率更高的架构。文献［12］设计了5 种不同的搜索空间，以分析DARTS 的退化问题，然后提出了L2 正则化方法以改善该问题。文献［13］提出了随机神经网络架构搜索（Stochastic Neural Architecture Search，SNAS）算法，通过限制架构参数为独热编码（one-hot）形式构建超网络，以改善DARTS 因派生cell 的方法而导致超网络与派生架构出现性能“鸿沟”的问题。文献［14］提出了公平的可微分网络架构搜索（Fair-DARTS）方法，采用S 状弯曲（Sigmoid）函数替换软最大（Softmax）函数，使各架构参数能公平地竞争，并设计了“零一”损失（zero-one loss）正则化项促使架构参数向0 或1 收敛。尽管以上研究从不同角度分析了DARTS 方法存在的问题，也提出了相应改进，但很少有文献从搜索空间的角度分析和改进DARTS。

针对上述问题，本文提出了优化搜索空间下带约束的可微分神经网络架构搜索算法。首先，以架构参数为量化指标，本文绘制了各架构参数在DARTS 超网络优化过程中的变化曲线，结合其派生策略，指出DARTS 派生架构性能欠佳的问题，根源上是由其搜索空间的设计导致的，并针对该问题改进了搜索空间的设计。然后，受文献［13］启发，在优化搜索空间的基础上，针对DARTS 因派生策略而导致架构决策确定性不足的问题［13］，本文将架构熵引入DARTS，并将其作为超网络待优化目标函数的约束项，促使超网络得到确定性更高、表现更好的架构。最后，本文在CIFAR-10 数据集上进行了实验，算法搜索环节仅耗时8.5 h，算法评测环节中，搜得的架构在该数据集上取得了97.17%的分类准确率。实验结果表明，本文提出的改进方法是有效的，并且提升了搜得网络架构的表现。

1 DARTS算法

类似于人工设计方法中模块化的设计思想，DARTS 以cell 为架构搜索的基本单元，并用有向无环图表示［10］。该图包含若干有序结点和连接结点的有向边，其中，结点表示网络的特征图，有向边表示结点间的变换操作。DARTS 定义的cell 共7 个有序结点，分别是2 个输入结点（编号k-2、k-1）、4 个中间结点（编号0、1、2、3）和1 个输出结点（output）。其中，各中间结点，每个都通过有向边与输入结点和其前序的中间结点相连，定义如式（1）所示：

其中：x(j)代表cell 的中间结点，x(i)代表x(j)的前序结点，o(i，j)代表连接x(j)和x(i)的变换操作，i和j代表结点序号。

DARTS 向cell 中引入了架构参数α，并以堆叠的cell 构建超网络进行端到端的训练，把离散的架构搜索问题转化为连续空间的参数优化问题。该算法主要包含架构搜索和架构评测两个环节。

在架构搜索环节，cell 中的边代表的变换操作，是候选操作和架构参数加权求和的混合操作，其中各架构参数作为对应候选操作的权重。为了使各架构参数具有相同的取值范围，该算法采用了Softmax 函数对各架构参数进行松弛化操作，把架构参数的值归一化到（0，1）区间。经Softmax 后，式（1）中的变换操作重写如下：

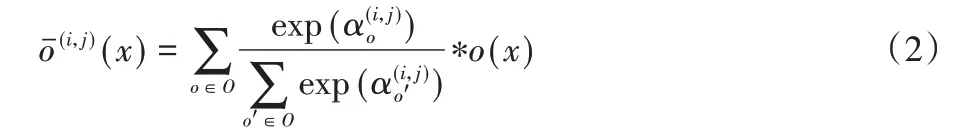
其中：o(x)表示候选操作表示松弛化后的变换操作，表示有向边(i，j)中候选操作o或o′对应的架构参数，i和j表示结点序号。O表示候选操作集合，共包含8 个候选操作，分别为3×3/5×5 可分离卷积（sep_conv）、3×3/5×5 空洞 可分离卷积（dil_conv）、3×3平均/最大池化（avg/max_pool）、跳连操作（skip_connect）和无连接（none）。

在架构评测环节，DARTS 先对搜索环节得到的cell 进行派生，得到简化的cell。派生过程包含两步简化操作，分别为1）候选操作简化：在有向边包含的8 个候选操作中，仅保留权重最大（none 除外）的操作。2）有向边简化：经候选操作简化后，在各中间结点与所前序结点相连的边中，仅保留包含权重top-2 的两条边。然后，以简化的cell 构建评测网络，以评测结果作为搜得架构的评价指标。

2 改进的可微分网络架构搜索

本章介绍如何从有向边和超网络两个层面提升DARTS算法的确定性。本文2.1 节分析了DARTS 算法中搜索空间设计导致搜得架构性能欠佳的问题，并设计了优化的搜索空间。2.2 节分析DARTS 算法超网络存在的确定性不足的问题，并针对性地向DARTS 引入架构熵作为目标函数的约束项。

2.1 优化DARTS的搜索空间

根据DARTS 算法的策略，在搜索环节，cell 中的每条有向边代表的变换操作都由式（2）定义。该公式从两个角度定义了架构参数：1）各架构参数作为权重，衡量了候选架构在变换操作中的重要性；2）松弛化架构参数，不仅将各架构参数归一化到（0，1）区间，还限制了有向边中各候选操作对应的架构参数之和为1。通过该公式的限制，算法的预期目标是，超网络优化完成后，以架构参数为量化指标比较各候选操作的重要性，并保留架构参数最大的候选操作作为最优操作。

为了分析上述策略是否达到预期目标，本文以具有代表性的有向边Edge（k-2，0）（其中，k-2 和0 表示结点编号）和有向边Edge（0，1）为例，绘制边中架构参数随超网络优化次数的变化曲线，如图1（a）（b）所示。本文发现，所有有向边中的架构参数主要呈现这两种变化趋势：如图1（a）的变化趋势，出现在中间各结点最浅的连接边（即中间结点与输入结点的连接边）中；如图1（b）的变化趋势，出现在其他所有的较深的边中。

图1（a）中，各架构参数取值较为分散，按派生策略步骤1）胜出的候选操作，基本能实现DARTS 算法以架构参数选优的设计思想。图1（b）中，none 操作对应的架构参数最大，且具有压倒性的优势，同时由于所有架构参数之和为1，其他候选操作对应的架构参数，被压制在很小的取值范围内，且取值区分很小。根据DARTS 的派生策略步骤1），none 操作不参与最大权重评比［10］。该策略造成了在深层边中，采用以架构参数为量化指标确定最优候选操作时，对派生无效的none 操作挤压了其他有效的候选操作，而有效候选操作的对应架构参数却很小。这就不能很好地实现算法以架构参数选择最优候选操作的设想。派生策略步骤1）带来的问题，还进一步影响了派生策略步骤2）。在有向边简化时，深层边中保留下来的有效候选操作，对应的架构参数取值较小，难以平等地与浅层边保留的有效候选操作进行竞争。因此，该算法最终偏向于浅层连接的cell 架构。文献［17］也发现了该问题，并指出这类cell 的泛化性欠佳。

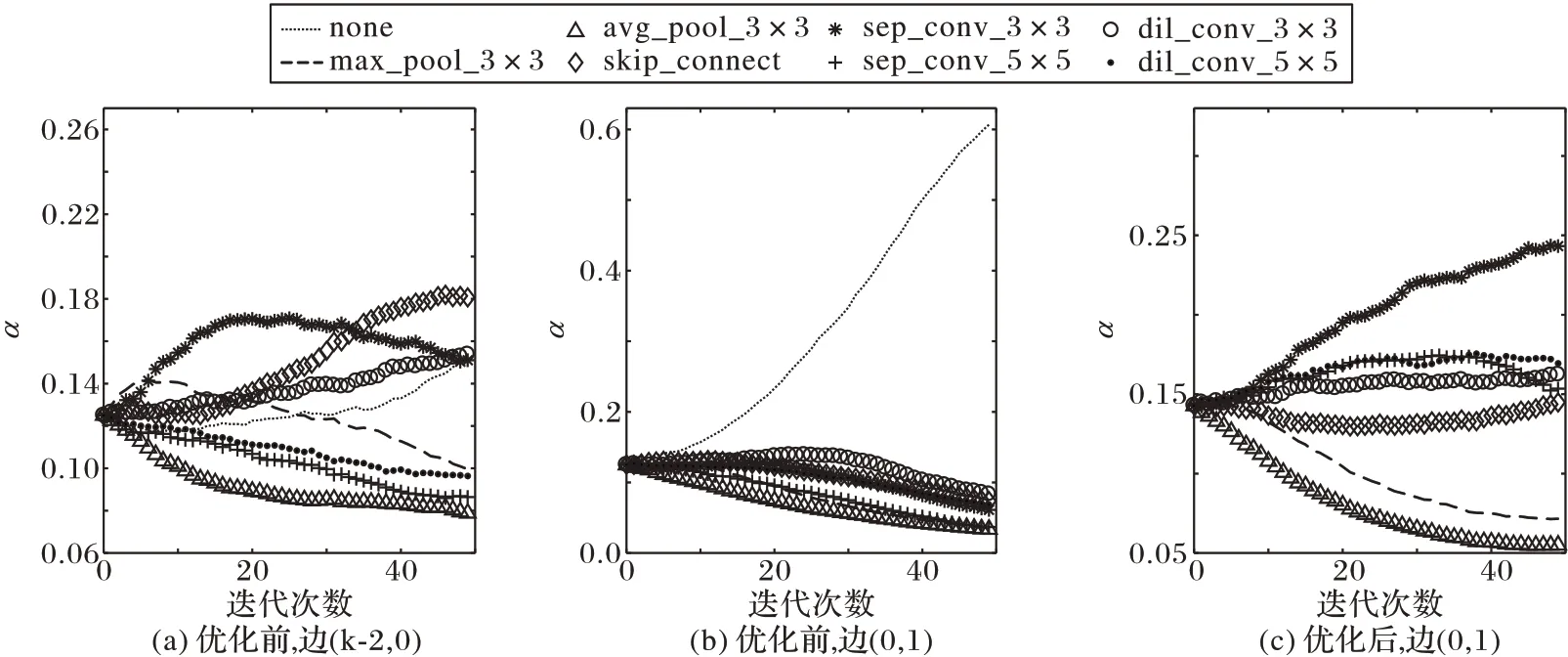
图1 两种典型的架构参数变化曲线Fig.1 Two typical curves of changing trends of architecture parameters

由以上分析可知，派生时在有向边中，none 操作不参与评比的策略引入了人为干预，其派生得到的最优候选操作，与超网络自动确定的最优操作并非完全一致。处理该问题最自然的办法是，在有向边中简化候选操作时，平等地对待none 操作与其他操作。但这种处理方式将导致派生cell 中none 操作过多而有效的卷积操作过少，从而造成派生得到的cell 过于简单，同时其表征能力大幅下降。文献［10］讨论了这种处理方式但未采用。

本文认为上述问题的根源，是候选操作集合中包含了对派生无效的none 操作。从DARTS 的派生策略角度看，搜索环节定义的cell 引入了none 操作，并最终导致无效的none 操作在派生环节占据了值最大的架构参数。本文在以上实验和分析的基础上，设计了优化的搜索空间，其候选操作集排除了none 操作，仅包含有7 个有效的候选操作。在较浅的边中，搜索空间优化前的架构参数演变趋势均如图1（a）所示。在较深的边中，搜索空间优化前后的架构参数演变，分别如图1（b）（c）所示。搜索空间优化前，图1（b）中的none 操作在该深层边中具有压倒性优势，其他各候选操作受到严重的影响，最优操作对应的架构参数αdil_conv_3×3=0.08。搜索空间优化后，图1（c）中的各候选操作对应架构参数的取值较图1（b）更加分散，且最优候选操作的架构参数αdil_conv_3×3=0.24，大于优化前。对比可见，仍以架构参数为量化指标选择最优候选操作，优化后的搜索空间能使有效的候选操作在派生时胜出。在有向边简化时，深层边中胜出的候选操作能在相同的条件下与浅层边胜出的候选操作公平地比较，更符合搜索算法和派生策略的预期。

2.2 提升搜索超网络的确定性

DARTS 方法创造性地把架构参数融入了搜索cell 的定义中，在架构搜索环节，该策略能把离散的架构搜索问题转化为连续参数空间的参数优化问题。在架构评测环节，这些被优化的架构参数需要从连续空间的表现形式转换为独热编码（one-hot）的离散表现形式。为此，DARTS 设计了对应的派生策略。尽管该策略能够离散化架构参数，得到派生的cell，但架构参数在这两种表现形式上的差异却未能得到很好的处理。为了量化上述差异，文献［16］在有向边层面，将架构参数和熵联系起来定义了确定性，以定量地衡量派生的网络架构是参数空间中是最优架构的可能性大小。文献［16］认为，DARTS 在超网络的搜索训练完成后，每条边的架构参数分布仍然拥有相对较高的熵，较高的熵意味着超网络对搜索到架构的确定性偏低，即派生得到的架构是优架构的可能性偏低。低确定性进而造成了超网络与派生得到的架构在验证集上的表现出现“鸿沟”（gap），即超网络在验证集上的准确率较高，但派生得到的架构（未重新训练时）在验证集的准确率与前者相差很大。在超网络的优化过程中，如果搜索算法能让架构参数以最终要输出的离散形式为目标，促使架构参数向one-hot 向量的形式演变，则可以降低架构熵，提升超网络对搜索结果的确定性，缩小架构参数在连续和离散两种形式之间的差异。

文献［14］提出的0-1 损失函数，就是为了促使架构参数向0 或1 趋近。不同于文献［14］方法，受文献［13］启发，本文按照DARTS 对cell 的定义，把归一化到（0，1）区间的架构参数，看作对应候选操作被超网络选为最优操作的概率，结合熵的定义，以所有归一化的架构参数向量为基础，定义了架构熵，如式（3）所示。该指标衡量了超网络对搜索结果的确定性，降低架构熵可提升超网络的确定性。

其中：Lentropy表示架构熵，表示归一化的架构参数，（i，j）表示结点i和结点j 之间的有向边。

本文将Lentropy作为约束项，引入DARTS 方法的架构搜索环节的目标函数，以减小架构参数两种形式之间存在的差异，提升超网络对搜得架构的确定性。超网络目标函数的定义，如式（4）所示。

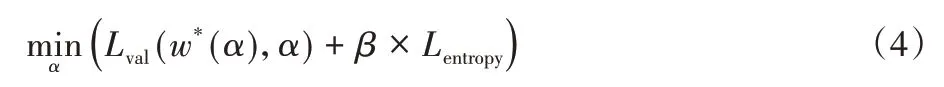
其中：Lval表示验证集损失，w表示候选操作中的卷积核参数，β为平衡Lval和Lentropy的系数。

如图2 所示，以式（3）定义的架构熵为量化指标，对比引入约束项前后该值随超网络训练过程的变化曲线。可见，引入Lentropy后，架构熵明显降低（均采用前文改进的搜索空间）。这表明本文提升超网络确定性的方法是有效的。

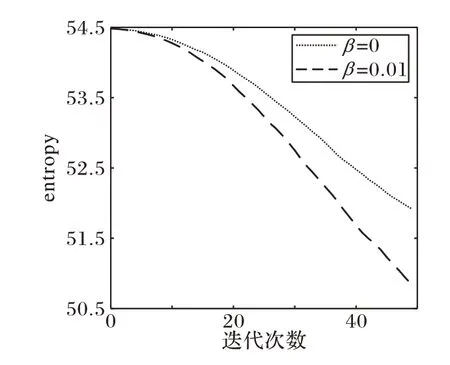
图2 约束项引入前后的架构熵对比Fig.2 Comparison of architecture entropy before and after introducing constraint

3 实验设计及结果

本文搜索阶段实验的操作系统为Windows 10，处理器为Intel i7-7800X，GPU 为1*Nvidia GeForce GTX 1080Ti。评测阶段实验操作系统为Ubuntu 16.04，处理器为2*Xeon E5，测试使用的显卡为2*Nvidia GeForce GTX 1080Ti。编程语言均为Python 3.6，深度学习框架均为Pytorch。

3.1 实验数据集

本文与相关研究［10，13-16］保持一致，采用图像分类数据集CIFAR-10 进行架构搜索和架构评测实验。该数据集的训练集含50 000 张分辨率为32×32 的图像，测试集含10 000 张分辨率为32×32 的图像，两者的图像类别均为10 类。在架构搜索环节，本文沿用DARTS 的超网络训练策略［10］，把训练集均分为两个子集，其中一个子集用于训练候选操作，另一个子集用于训练架构参数。在架构评测环节，以简化的cell 构建评测网络，重新初始化后，在CIFAR-10 的完整训练集上进行训练，在测试集上进行评测，并以测试准确率作为搜得架构的评价指标。

3.2 约束项的系数选择

约束项系数β起到平衡两个损失项的作用，其值的选择非常重要。本文设计了一组对比实验，以确定适合的取值。实验中严格控制其他变量，仅分别设置β=0、0.01、0.1、1。每组实验重复4 次完整的架构搜索和架构评测实验，并计算4 次评测结果的平均值，以此作为β的选择依据。如表1 所示，当β=0.01 时，4 次实验的平均准确率最高。因此，本文以β=0.01 进行后续实验。

表1 CIFAR-10数据集上β不同取值时的平均准确率Tab.1 Average accuracy on CIFAR-10 dataset with different β

3.3 实验结果

在架构搜索环节，本文采用了与DARTS 方法完全一致的超网络［10］。该超网络初始通道数为16，共包含8 个cell，其中第3 个和第6 个cell 为起降维作用的reduction cell，其余cell 为起特征提取作用的normal cell。超网络优化时，本文采用DARTS 算法的一阶近似优化策略。超网络训练共50 个周期，数据批大小为64。优化候选操作的卷积核参数w时，采用随机梯度下降（Stochastic Gradient Descent，SGD）算法，初始学习率lrw=0.025，动量momentum=0.9，权重衰减系数为3×10-4。优化架构参数α时，采用自适应动量估计（Adaptive moment estimation，Adam）算法，初始学习率lrα=3×10-4，权重衰减系数为10-4。

在以上实验设置下，本文搜索的架构如图3 所示。

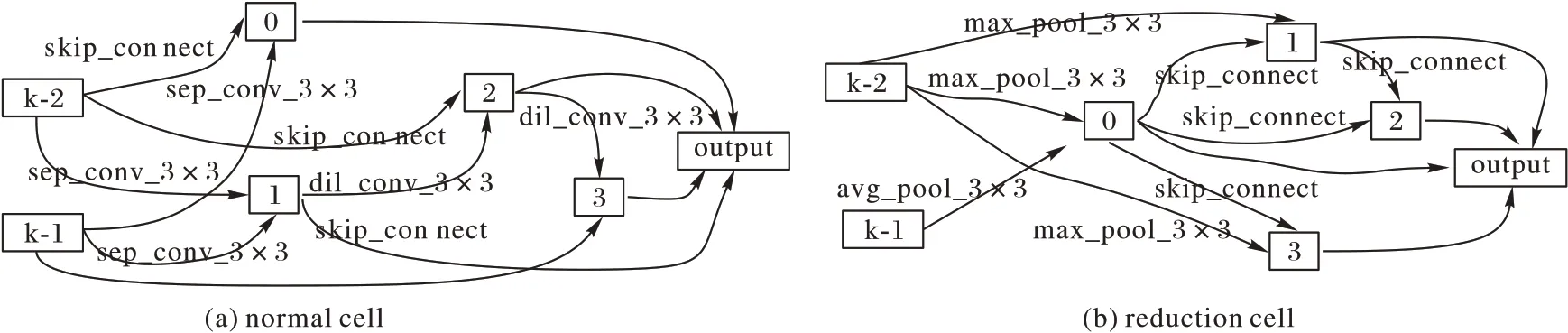
图3 CIFAR-10数据集上搜索到的cellsFig.3 Searched cells on CIFAR-10 dataset

与DARTS 方法搜得的cell［10］相比，本文搜得的cell 拥有层数更多，结构更深。在2.1 节中，本文分析了DARTS 搜得cell 较浅的原因，该实验结果印证了相关的分析。采用与DARTS 相同的设置［10］，本文以cell 数量d=20 构建评测网络。在CIFAR-10 上的评测结果，以及与相关方法所得架构在该数据集分类准确率的对比，如表2 所示。

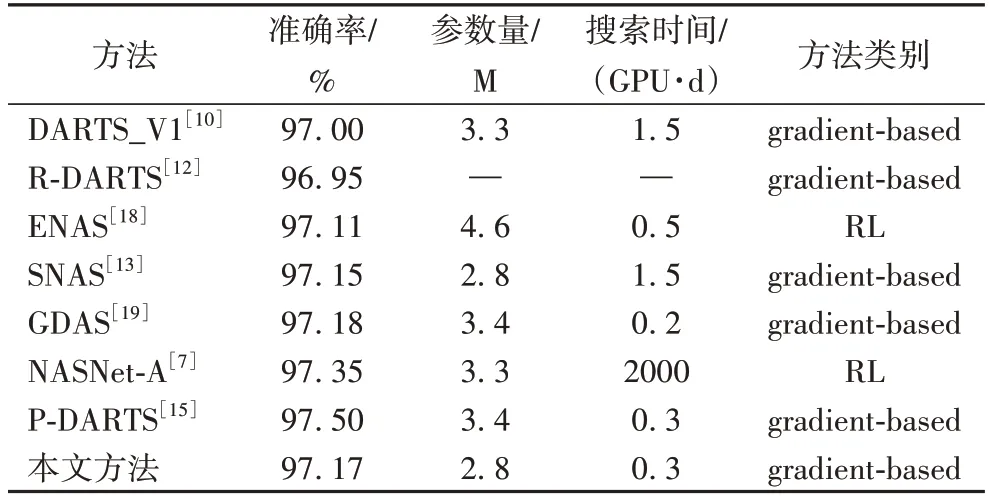
表2 与相关方法在CIFAR-10数据集上的准确率对比Tab.2 Accuracy comparison with related methods on CIFAR-10 dataset

对比方法中，NASNet-A（由谷歌大脑的研究人员提出并命名）来源于文献［7］，鲁棒的可微分架构搜索（Robust Differentiable ARchiTecture Search，R-DARTS）来源于文献［12］，渐近的可微分架构搜索（Progressive Differentiable ARchiTecture Search，P-DARTS）来源于文献［15］，高效的神经网络架构搜索（Efficient Neural Architecture Search，ENAS）来源于文献［18］，使用可微分架构采样的基于梯度的搜索方法（Gradient-based searching approach using Differentiable Architecture Sampling，GDAS）来源于文献［19］。表中参数量的单位为M，表示106。

由表2，本文构建的评测网络在CIFAR-10 上，测试准确率为97.17%。与DARTS 采用相同的一阶近似优化策略（DARTS_V1），本文在DARTS 的基础上提升了0.17 个百分点。同时，本文架构的测试准确率还高于ENAS 和SNAS。对比各方法的搜索时间，本文的架构搜索时间与P-DARTS相近，具有较高的搜索效率。综上，本文提出的方法是有效的，通过提升搜索算法对架构的确定性，既提升了DARTS 算法的架构搜索效率，还搜索到了性能更好的架构。

4 结语

本文从搜索空间设计和超网络目标函数两个方面分析了DARTS 算法存在的问题，针对性地设计了优化的搜索空间，并引入了架构熵作为超网络目标函数的约束项。优化的搜索空间有效地避免了none 操作挤压其他候选操作的问题，同时精简的搜索空间还提升了架构搜索效率。引入架构熵，促使超网络以派生架构的形态为目标进行架构搜索，最终搜得的架构在CIFAR-10 上取得了更高的准确率。实验结果表明，本文所提方法是有效的，提升了搜索环节对搜得架构的确定性。搜索空间是NAS 的基础，本文认为未来工作可关注如何设计更具表现力的搜索空间。