竹材宏观微观力学性能试验与数值模拟

王志威，张晓伟*，姚利宏，张庆明

(1. 北京理工大学爆炸科学与技术国家重点实验室，北京 100081；2. 内蒙古农业大学材料科学与艺术设计学院，呼和浩特 010018)

竹材具有生长快、产量高、力学性能优异等特点，在日常生产生活中应用广泛。随着自然资源的日益稀少和人类对生态环境的重视，竹材作为一种可再生的环保性材料，越来越具有广阔的应用前景。在微观结构上，竹材是一种典型的单向纤维增强复合材料[1]，其力学性能和破坏规律取决于各个组分的力学性质、体积分数、含水率等因素。

针对竹材组成结构与其力学性质的关系，研究者们进行了大量的研究工作。Williams等[2]研究发现，竹材的弹性模量、剪切模量、泊松比与纤维密度呈线性关系。Moran等[3]和Deng等[4]分别研究了竹材的横纹和顺纹压缩力学性能。Yang等[5]研究了纤维方向与层合方向不同夹角试件的力学性能，提出了基于指数和正弦函数的经验公式来预测抗压强度。刘焕荣[6]进行了从竹黄到竹青的分层竹片拉伸试验，结果表明竹青部位的弹性模量和抗拉强度分别约为竹黄的5倍和3倍。Zhao等[7]建立了竹秆轴向抗压数值模型，通过与试验结果比较，验证了模型的有效性。近年来，许多学者还对竹龄[8]和不同产地的竹材[9]、竹材的微观结构特性[10]、竹材组分中单根纤维束的力学性质[11]及复合竹材的力学性能[12-13]方面进行了大量研究。

目前，根据竹材的结构特点，考虑到竹基重组材料和竹纤维复合材料在工程中得到了广泛的研究和应用[14-15]，因此，竹材纤维和基体的力学性能对于该类材料工程应用具有重要意义。本研究结合细观力学和材料力学方法得到了一种确定竹材纤维和基体材料力学性能参数的计算方法：首先通过竹材的压缩、拉伸和弯曲试验获得竹材的宏观力学参数；然后基于试验结果和细观力学分析方法，得到竹材中纤维和基体的力学参数；最后根据各组分力学参数构建数值计算模型，通过模拟与试验结果的比较进一步验证材料参数的有效性。

1 材料与方法

试验所用竹材取自浙江安吉，取3年生毛竹(Phyllostachysedulis)竹秆的中部区域，离地高度约为1.8 m，胸径为10～12 cm，壁厚约10 mm，含水率约为10.4%，密度为857 kg/m3。根据已有研究成果，竹材在横纹径向和弦向压缩下的宏观力学性能基本相似[16]，故仅考虑竹材在顺纹和横纹径向压缩下的力学行为，如图1所示，制备了竹材准静态压缩试件。试件尺寸为10 mm(L)×7.4 mm(W)×10 mm(H)，其中L、W和H分别表示沿横纹弦向、横纹径向和顺纹方向长度。参照GB/T 15780—1995《竹材物理力学性质试验方法》，选用万能力学试验机，顺纹加载速度为0.60 mm/min，横纹加载速度为0.42 mm/min。试验过程中，为了保证重复性，每个工况至少进行3次有效试验。

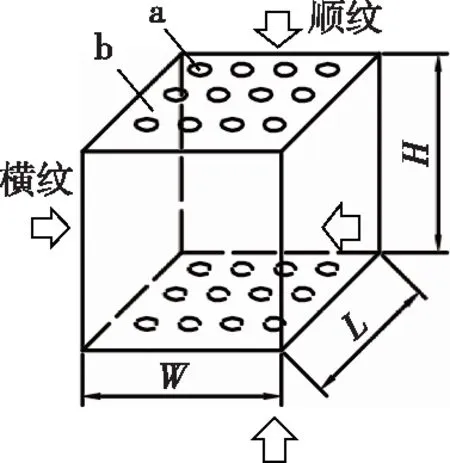
注：a为纤维；b为基体。图1 试件在不同方向加载示意图Fig. 1 Schematic diagram of the bamboo specimen loading in different directions

竹材拉伸试件为哑铃型，如图2所示，试件长度方向为纤维方向，厚度方向为径向。两侧夹持处厚7.4 mm、宽16 mm，中间试验段厚3 mm、宽8 mm、长30 mm。在试验中使用25 mm引伸计，拉伸速度设为1.80 mm/min。

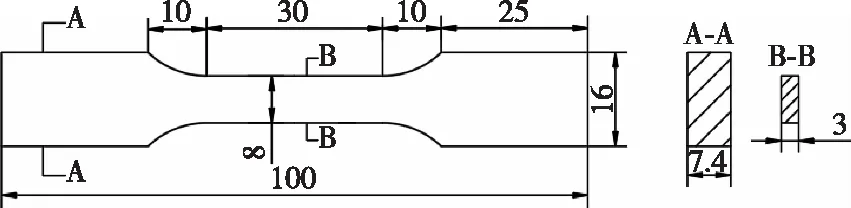
图2 竹材拉伸试件的形状和尺寸Fig. 2 Shape and size of the bamboo tensile specimen

在弯曲试验中载荷方向沿横纹径向，试件长100 mm、宽20 mm、厚7.4 mm，竹青部分朝上，竹黄部分朝下。加载方式为三点弯曲，两支座间跨距为76 mm，加载速度为0.44 mm/min。

2 结果与分析

2.1 宏观力学性能分析

2.1.1 压缩性能

根据试验得到的压缩应力-应变曲线如图3所示，可见试验重复性较好。图3a为顺纹压缩结果，竹材首先经历了弹性变形，在应变约为0.03(B点)时，进入塑性屈服阶段，屈服应力为65.97 MPa。经过一段强化段后，在应变约为0.25(C点)时，应力增加到87.78 MPa，之后应力随着应变的增加而减小。当试件变形到42%(D点)时，压缩应力出现一个极小值，约为58.82 MPa。随后进入致密阶段，应力随着应变的增加而陡然上升。图3b为沿横纹压缩得到的应力-应变曲线，和图3a顺纹压缩试验曲线不同，横纹准静态压缩过程中应力与应变的关系和泡沫材料的压缩行为相似，呈单调增加。在应变约为0.03(B点)时，试件进入塑性屈服阶段，屈服应力为25.18 MPa。之后随着应变的增加，应力增加的速度由慢到快，先是经过一段线性弱强化阶段到达C点，随后进入幂强化阶段即致密化阶段，应力随应变的增加快速增长。

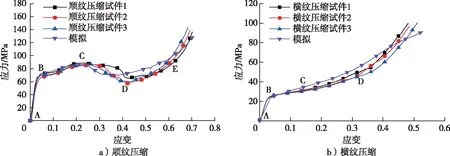
图3 竹材压缩应力-应变曲线Fig. 3 Compression stress-strain curves of the bamboo specimens

试验过程中，试件沿顺纹和横纹方向的压缩变形情况分别如图4和5所示。结合图3a和图4可知，试件在弹性变形之后进入屈服阶段，此时竹材中纤维材料屈服，基体材料变形很小，纤维材料中的维管束细胞在周围基体材料的簇拥下稳定性增强，使得屈服后进入一段塑性强化阶段。之后试件继续被压缩(图4b)，此时维管束发生屈曲，试件失稳，当试件继续变形(图4c)时，基体材料被压溃，随后进入致密阶段。由图5可见，在横纹方向下压缩的形态变化主要表现为基体组织的塌陷、压扁直至压溃。结合图3b可知，试件首先经历弹性段，之后由于下方纤维含量相对较少，下方的基体组织先被压溃(图5b)，继续压缩出现剪切失效，当基体组织完全塌陷时，试件便进入压实阶段。

图4 顺纹压缩变形Fig. 4 Deformation under the longitudinal compression

图5 横纹压缩变形Fig. 5 Deformation under the transverse compression

2.1.2 拉伸性能

竹材的顺纹拉伸应力-应变曲线如图6所示。竹材顺纹拉伸呈脆性断裂特征，应力首先随应变呈线性增长，当应力达到110～120 MPa时试件发生脆性断裂。根据曲线拟合得到竹材拉伸弹性模量约为12.4 GPa，抗拉强度平均约为115 MPa。观察试样的断裂形貌(图7)可以看出，试样在断裂口处参差不齐，断面处所在平面与纤维方向基本垂直。

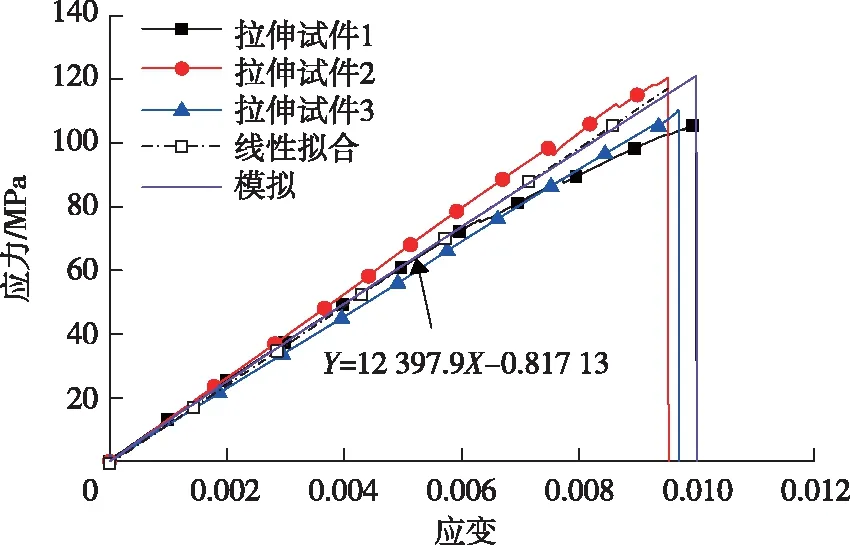
图6 竹材拉伸应力-应变曲线Fig. 6 Tensile stress-strain curves of bamboo specimens

图7 竹材拉伸脆性断裂Fig. 7 Tension brittle fracture of bamboo

2.1.3 弯曲性能

试验得到的竹材弯曲破坏形态如图8所示，荷载-位移曲线如图9所示，试件经历了弹性变形阶段(Ⅰ阶段)和断裂失效阶段(Ⅱ阶段)。当荷载增加到1 070 N时，最外层竹纤维开始发生断裂，并从外向内逐层持续受拉至完全断裂，荷载随着位移的增加逐渐下降。

图8 竹材试件的弯曲破坏Fig. 8 Bending failure of bamboo specimen

图9 竹材三点弯曲荷载-位移曲线Fig. 9 Load-displacement curves of three-point bending of bamboo specimens

2.2 纤维和基体的力学参数确定

在竹材宏观力学性能试验的基础上，通过图像处理方法确定各组分的体积分数，然后根据细观力学和材料力学方法对纤维和基体的力学性质进行分析，以确定各组分的力学参数。

2.2.1 纤维体积分数

首先，采用光学显微镜LV100ND拍摄了竹材压缩试件的横截面图像，如图10a所示。竹材中纤维密度沿径向由内向外逐渐增大。运用图像处理软件Digimizer自动识别纤维区域，并将纤维区域单独标注出来(图10b中红色部分)，通过软件自动识别出红色区域的面积，将其除以竹材横截面总面积即可得到该试件的纤维面积比，即纤维体积分数。考虑到竹材纤维体积分数存在梯度变化，将试件沿厚度方向分成4个区域，每个区域的纤维体积分数分别为14.57%，18.71%，26.94%，39.68%。纤维体积分数(Vf)与沿径向由内向外的位置分数(x/B)之间近似呈线性关系，如图11所示。图10中纤维平均体积分数为25%，将剩余部分看做是基体材料，其占比为75%。拉伸试样试验段横截面尺寸为8 mm×3 mm，位于夹持段横截面的中心位置，纤维体积分数也是25%。弯曲试样的横截面尺寸为20 mm×7.4 mm，纤维体积分数和图10b相同。

图10 压缩横截面上纤维组分的识别Fig. 10 Identification of fiber components at the cross section

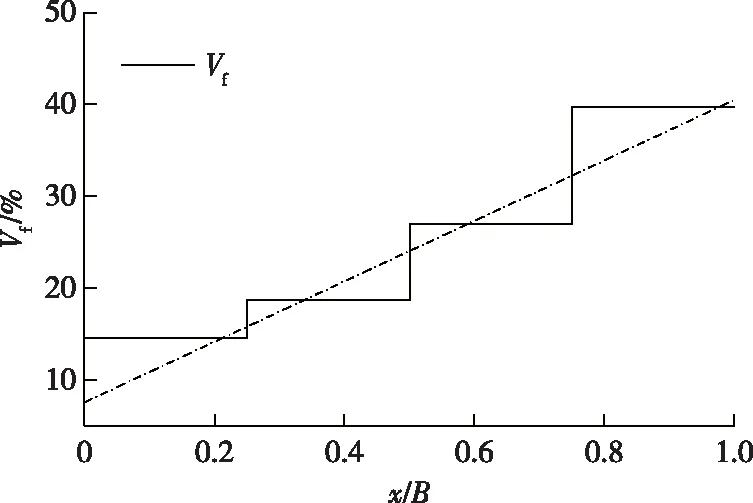
图11 纤维体积分数与位置分数的关系Fig. 11 Relationship between fiber volume fraction and position fraction

2.2.2 各组分力学参数

竹材顺纹受压和顺纹受拉弹性模量基本相等[17]，由于顺纹拉伸过程中使用了引伸计，得到的顺纹受拉弹性模量相对准确，故弹性模量取值为12.4 GPa。根据顺纹压缩试验所得应力-应变曲线，当纤维含量为25%时，屈服强度为65.97 MPa，而横纹压缩试验所得屈服强度为25.18 MPa。假设纤维材料与基体材料是各向同性的，根据竹材在横纹受压时主要表现为基体材料的破坏，因此，将横纹压缩得到的屈服强度当作基体材料的强度。根据复合材料细观力学的混合定律[18]，记σcy、σf-cy、σm-cy分别为作用在竹材整体、纤维和基体上的屈服应力，Ec、Ef、Em为相应的弹性模量，两组分的体积分数分别为Vf、Vm，且Vf+Vm=1，则竹材整体的应力与各组分应力及体积分数的关系为：

σcy=σf-cyVf+σm-cyVm

(1)

竹材整体的压缩弹性模量Ec与各组分弹性模量及体积分数的关系为：

Ec=EfVf+EmVm

(2)

根据式(1)有：

65.97=0.25×σf-cy+0.75×25.18

可得σf-cy=188.34 MPa、σm-cy=25.18 MPa。

根据式(2)有：

12.4×109=Ef×0.25+Em×0.75

(3)

将弯曲横截面均匀分为4份，自上而下每一层的弹性模量分别为E1、E2、E3、E4，根据每一层的纤维体积分数可得：

E1=0.396 8Ef+0.603 2Em

(4)

E2=0.269 4Ef+0.730 6Em

(5)

E3=0.187 1Ef+0.812 9Em

(6)

E4=0.145 7Ef+0.854 3Em

(7)

设弯曲试件的中性轴与上表面距离为yc，应变ε=y/ρ，如图12所示，利用截面轴力为零的条件确定中性轴位置：

(8)

式中：A1、A2、A3、A4为每一层的面积；ρ为曲率半径。

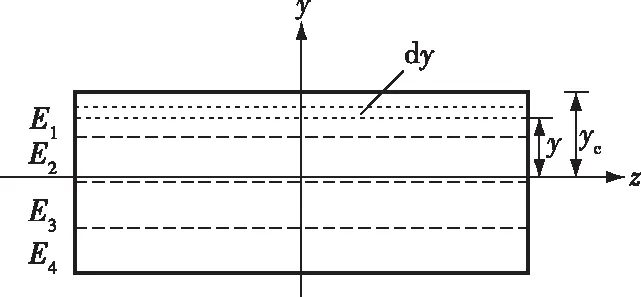
图12 竹材弯曲试件的横截面示意图Fig. 12 Diagram of cross section of the bamboo specimen for bending

横截面上的弯矩M为各层对中性轴的弯矩累加：

(9)

在弹性范围内，取弯曲荷载-位移曲线弹性段一点，荷载F=600 N、位移s=0.9 mm、跨距l=76 mm，可得M=11.4 N·m、ρ=0.802 m。联立式(3)～(9)可得Ef=21.43 GPa、Em=9.39 GPa、yc=3.51 mm。

根据式(9)可得：

(10)

式中，I1、I2、I3、I4分别代表截面1、2、3、4对中性轴的惯性矩，从而可得截面4的弯曲正应力：

(11)

由弯曲荷载-位移曲线可知，当荷载为1 070 N时，弯矩为20.33 N·m，中性轴以下部分开始被拉断，最大拉应力在下表面处，此时y=3.89 mm，代入式(11)可得断裂强度σtb=96.39 MPa，由最下层纤维体积分数Vf=14.57%，设纤维和基体的拉伸断裂强度分为σf-tb、σm-tb，则有：

96.39=σf-tb×0.145 7+σm-tb×0.854 3

(12)

由拉伸应力-应变曲线，可知当纤维体积分数为25%时，σtb=115 MPa，可得：

115=σf-tb×0.25+σm-tb×0.75

(13)

由式(12)和(13)，可得σf-tb=248.83 MPa、σm-tb=70.39 MPa。

基体材料的塑性参数根据横纹压缩应力-应变曲线获得，由于在横纹压缩时强度尚未达到纤维材料的屈服强度，故纤维变形很小，可认为横纹压缩仅表现为基体材料受压，由此可得基体材料的应力-应变关系如图13a所示。结合图3a和b，运用混合定律可得纤维材料的应力-应变关系(图13b)。

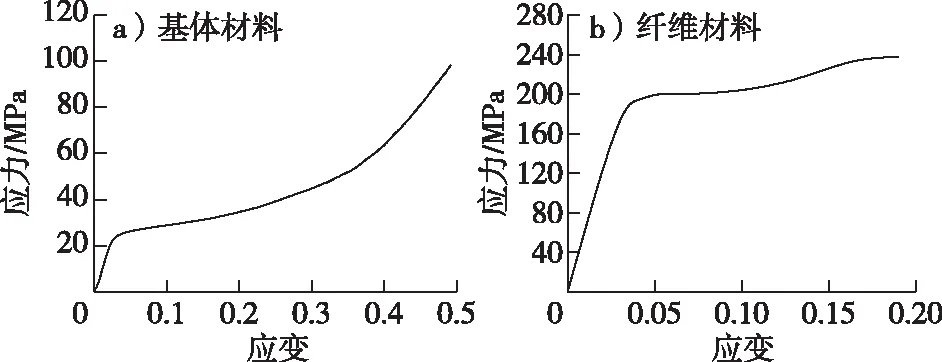
图13 各组分应力-应变关系Fig. 13 Stress-strain relationship of each component

3 数值模拟分析

根据上述所获得的竹材组分力学性能，通过ABAQUS数值模拟软件建立有限元模型，模拟竹材压缩、拉伸过程与试验进行比较，以验证上述材料参数的有效性。

3.1 模型的建立与材料参数定义

3.1.1 计算模型的建立

在建立压缩模型时，使用离散刚体单元建立上下压头，基体材料使用C3D8R的六面体实体单元，纤维材料用梁单元。将梁单元的个数设为81根，梁单元的横截面为圆柱形，半径0.361 9 mm、长度10 mm，基体材料尺寸为10 mm×10 mm×10 mm，则纤维材料体积为333 mm3，基体材料体积为1 000 mm3，计算可得纤维体积分数约为25%。顺纹压缩过程沿Z轴方向，横纹压缩过程沿Y轴方向，计算模型如图14所示，六面体单元划分为8 000个，梁单元划分为1 620个。

在建立拉伸模型时，只考虑试验段，基体材料使用均质实体单元，尺寸为8 mm×3 mm×30 mm，纤维采用梁单元，长度为30 mm。将梁单元的个数设为20根，梁单元的横截面半径为0.361 9 mm、长度为30 mm，则纤维材料体积为246.88 mm3，基体体积为720 mm3，计算可得纤维体积分数为 25.5%。拉伸过程沿Z轴方向，计算模型如图15所示，基体材料单元划分为19 440个，纤维材料划分为1 800个。

分析过程中，压头与试件加载面为通用约束，纤维内置于基体材料中，与基体共节点。试件的加载端通过压头产生一定的位移，而另一端固支，通过Abaqus/standard计算得到试件的压缩/拉伸应力-应变曲线。

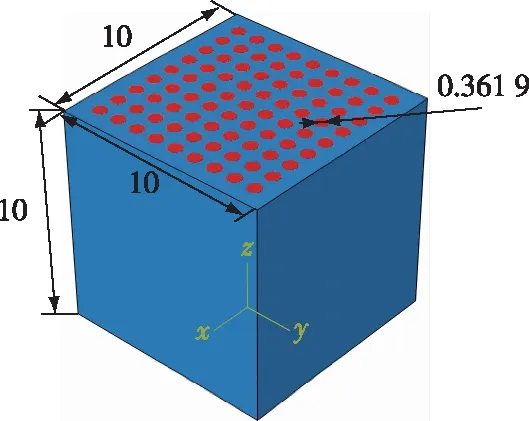
图14 压缩计算模型Fig. 14 Compression calculation model

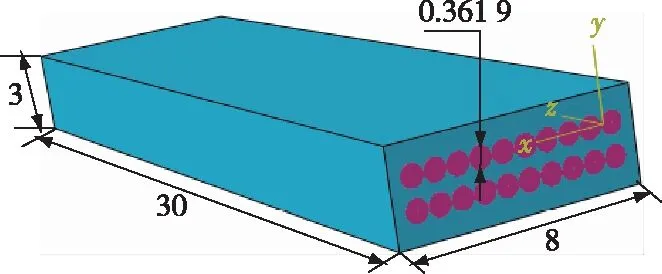
图15 拉伸计算模型Fig. 15 Tension calculation model

3.1.2 材料参数的定义

纤维材料与基体材料均采用各向同性弹塑性本构关系，弹性模量(E)、抗压屈服强度(σcy)、抗拉断裂强度(σtb)、泊松比(ν)[12]等定义见表1。塑性部分的参数根据图14中纤维、基体应力-应变曲线塑性段的数据依次输入30个点，采用最大拉应变失效准则，纤维和基体的失效应变均为0.1。

表1 纤维和基体材料的力学参数Table 1 Mechanical parameters of fiber and matrix material

3.2 模拟结果分析

3.2.1 顺纹压缩模拟结果

通过仿真计算得到的应力-位移曲线，处理得到的应力-应变关系曲线如图3a所示，纤维变形过程见图16。可以看出，纤维经历了屈曲、褶皱和压实过程。仿真结果和试验具有相同的变化趋势，得到的屈服强度为66.14 MPa，与试验得到的结果相对误差在10%以内，验证了数值模型和各组分参数的有效性，为竹材各组分力学性质的研究提供了参考。

图16 顺纹压缩模拟纤维变形图Fig. 16 Diagram of longitudinal compression simulated fiber deformation

3.2.2 横纹压缩模拟结果

通过仿真计算得到的应力-位移曲线，处理得到的应力-应变关系曲线如图3b所示，横纹压缩模拟得到的屈服强度为22.43 MPa。横纹压缩模拟变形图如图17所示，表现为基体材料的变形过程与试验相似，证明了通过建立细观力学模型研究单向纤维增强复合材料的可行性。

图17 横纹压缩模拟变形图Fig. 17 Diagram of transverse compression simulated deformation

3.2.3 拉伸模拟结果

通过仿真得到的拉伸应力-应变关系如图6所示，得到的拉伸强度为120 MPa，和试验结果相比误差在10%以内。拉伸模拟的变形图如图18所示，从断口可以看出基体材料完全断裂，纤维材料被抽拔出来。模拟结果和试验结果相似，证明了力学参数确定方法的有效性。

图18 拉伸模拟变形图Fig. 18 Diagram of tension deformation by simulation

4 结 论

对竹材在不同载荷条件下进行准静态试验研究，并根据试验得到的数据结合细观力学和材料力学方法，得到以下结论。

1)通过准静态压缩、拉伸、弯曲试验获得竹材的宏观力学性能。顺纹压缩时，竹材屈服后经历了一个强化段，然后由于纤维的屈曲失稳导致应力下降，最后应力再次上升，并逐渐被压实；而横纹压缩在弹性段之后进入线性弱强化阶段，随后进入致密化阶段。竹材的顺纹拉伸可近似视为脆性材料的断裂过程，弯曲过程中最外层竹纤维首先发生断裂。

2)在宏观压缩、拉伸和弯曲的力学性能试验基础上，采用图像处理方法获得各组分体积分数，结合细观力学和材料力学方法得到了一种近似计算竹材纤维和基体材料力学性能参数的方法，并获得了竹材试件各组分的力学性能参数。

3)根据竹材本身的特点，建立竹材压缩和拉伸的有限元模型，并结合纤维和基体材料的力学参数进行模拟计算。将模拟结果和试验进行对比，验证了数值模拟方法和材料参数的有效性，为后续研究提供参考。