基于双四连杆机构的缝合装置设计与研究

陈海松，周燕飞

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

在碳纤维立体织物的穿刺成型工艺中，当碳纤维纱线替换完织物上原有钢针后，需要进行纤维锁扣。其目的在于将织物上正交叠放的各层碳布缝合在一起，并在织物厚度方向引入纤维。这样既可以保证织物结构的整体性，又能提高立体织物的体积密度[1]。在目前的生产工艺中，缝合时所采用的线迹为单线链式线迹，即用单根连续的碳纤维纱线按指定方向进行相互嵌套锁扣，工作原理与缝纫机缝合织布类似[2]。

传统缝纫机在缝纫过程中，当机针穿过织布并回退形成线环时，依靠织布底部的直勾针或者旋梭来形成链式线迹。但由于碳纤维纱线是脆性材料，耐磨性和抗弯折能力较差，并且织物上穿刺钢针排布密集，间距较小，无论是采用旋梭还是直勾针摆动的缝合方式都难以实现较好的缝合效果[3-4]。由于发达国家的技术封锁，再加上我国对高性能复合材料的研究起步较晚，目前市面上还没有成熟的自动化缝合设备。国内企业在生产立体穿刺织物时，依旧采用人工操作的方式实现链式线迹。因为织物上钢针数量较多，且每替换一根钢针就需要进行一次缝合，工作量过于庞大，导致人工置换周期长，成本高，同时也难以保证缝合的质量。

为了实现自动化生产立体织物，提高缝合的效率和质量，本文在传统缝纫机缝合方式的基础上，提出了一种基于四连杆机构的缝合装置方案，运用两个勾针之间的运动配合实现纤维锁扣。

1 缝合装置结构设计

传统缝合方式难以适用立体织物中的纤维锁扣，本文采用双勾针的方式实现链式线迹，具体工作流程如图1所示。

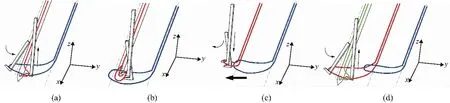
图1 双勾针实现链式线迹示意图

图1(a)为初始状态，此时勾针2处于极限位置，其上勾有上一个锁扣周期内形成的旧线环，勾针一穿过旧线环，处于置换钢针下方；图1(b)表示置换针回退形成新线环后，勾针1勾起新线环，此时新线环被勾针1从旧线环中带出，完成了线环的嵌套。同时，勾针2开始摆脱旧线环；图1(c)表示缝合装置移动到下一个缝合位置后，勾针1向下移动到初始位置，勾针2反方向摆动并勾住勾针1上的线环，然后也摆动到初始位置；图1(d)表示当两个勾针都摆动到初始位置后，进入下一个缝合周期，此时置换针开始形成新的线环，缝合装置重复上述动作。

从图1可知，勾针1是直线往复运动，勾针2是在平面内摆动。因此，可以用曲柄滑块机构驱动勾针1，用曲柄摇杆机构驱动勾针2。同时，要实现链式缝合，两个勾针在运动中需要满足一定的位置关系。如果采用两个驱动源分别驱动，难以保证两勾针的相对位置，本文将采用一个曲柄同时驱动两个四连杆机构的方式，并且为了简化结构，设定两个四连杆共用一个机架。其结构简图如图2所示。

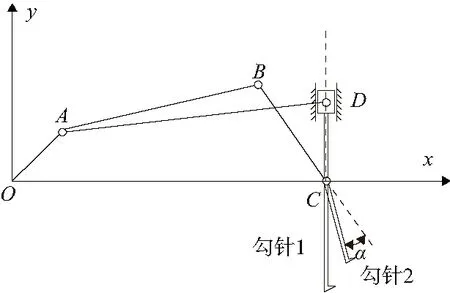
图2 缝合装置结构简图

根据缝合工艺要求，设定滑块的上极限位置为70mm，行程为15mm，勾针2摆动时的左右偏角均>5°。考虑安装空间，取装置安装高度为60mm。

为便于计算各杆长度，分别建立了曲柄滑块机构和曲柄摇杆机构的数学模型[5]，如图3、图4所示。

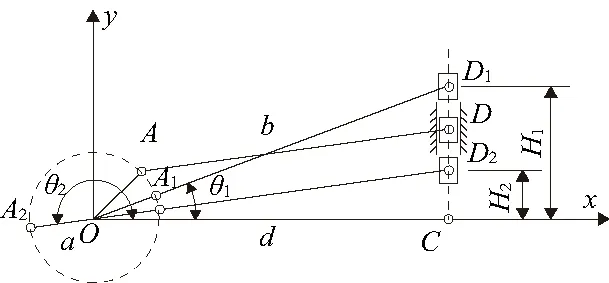
图3 曲柄滑块机构数学模型

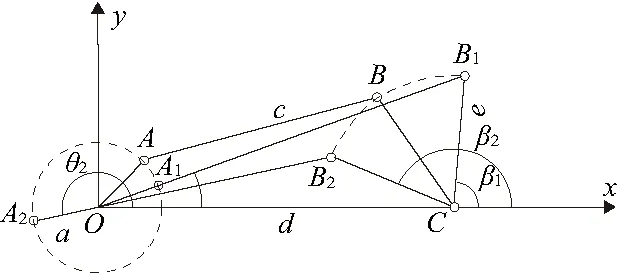
图4 曲柄摇杆机构数学模型

根据数学模型可建立以下方程式：

(1)

(2)

利用上述方程，结合勾针的极限位置，利用解析法计算出各杆长度，如表1所示。

表1 缝合装置参数 单位：mm

此时，当勾针2与摇杆的安装角为10°时，其左右偏角约为8°，满足设计要求。同时，根据缝合装置的安装高度和勾针的极限位置计算出勾针1的长度为117mm，勾针2长度为51mm。

2 缝合装置运动学分析

由于碳纤维纱线未加捻，抵抗冲击的能力较小[6]，因此需要对勾针的运动状态进行分析和仿真，以此来验证装置能否在满足工艺要求的情况下，对纱线的冲击和损伤较小。由于勾针1和勾针2分别固定在滑块和摇杆上，滑块和摇杆的运动参数直接反映了两个勾针的运动状态。因此，可通过研究滑块和摇杆的运动参数来分析两勾针的运动状态。

2.1 曲柄滑块机构

将曲柄滑块机构置于图5所示的坐标系中，以机架为x轴，滑块导路为y轴。令曲柄OA的长度矢量为a，连杆AD的长度矢量为b，机架CO的长度矢量为d，滑块距机架高度CD的长度矢量为h。其中φ1为曲柄与水平方向的夹角，φ2为连杆与水平方向的夹角。

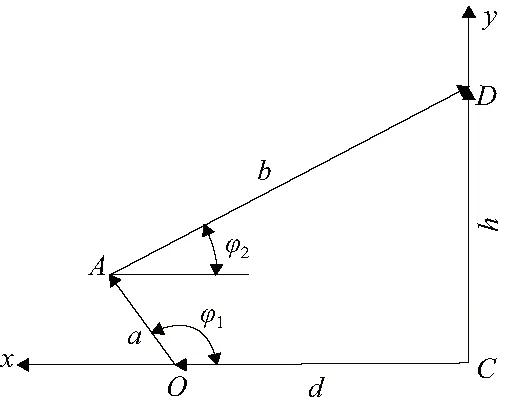
图5 曲柄滑块机构运动模型简图

由图5可知，该机构形成的封闭矢量多边形方程式为[7]

a+b+d=h

(3)

其复数形式为

aeiφ1+beiφ2=ih+d

(4)

将其展开后得到位移关系式：

(5)

将式(5)求导后并展开可得到其速度方程：

(6)

同理，对式(4)求导后得到其加速度方程：

(7)

2.2 曲柄摇杆机构

同理，将曲柄摇杆机构置于直角坐标系中，以曲柄转动中心为原点，机架为x轴，竖直方向为y轴，如图6所示。图中θ1表示曲柄与机架的夹角，由于两个四连杆机构采用同一个曲柄驱动，因此θ1与曲柄滑块中的φ1等同。θ2为连杆AB与水平面的夹角，θ3为摇杆BC与机架的夹角。

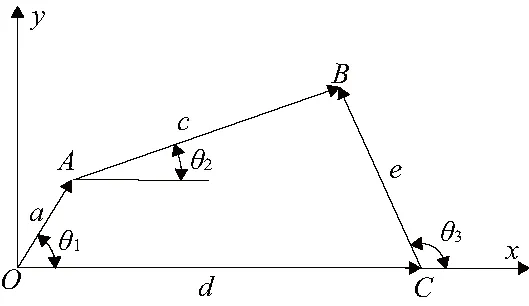
图6 曲柄摇杆机构运动模型简图

该机构的矢量方程为

a+c=d+e

(8)

同理可得，该机构中摇杆的角位移关系式：

(9)

式中：

(10)

角速度关系式：

(11)

角加速度关系式：

从上式中可以看出，在杆长一定时，滑块与摇杆的运动状态与曲柄的运动状态有直接关系[8]。因此驱动电机的控制算法会对锁扣装置运动的平稳性产生很大影响。

2.3 缝合装置运动状态仿真

由于在立体织物成型过程中，链式缝合不是持续进行，而是在碳纤维纱线替换完钢针并形成锁扣线环时缝合装置才开始运行，且在完成一次缝合后停止，等待下一次缝合。因此电机需要频繁的启动和停止。根据工艺要求，一次缝合周期为1s，曲柄在一个周期内需要旋转的角度为2 π。

为了削弱柔性冲击对缝合装置影响，提高缝合的成功率，改用S型速度曲线算法控制电机转速。在工业控制中，S型速度曲线一般分为7段，虽然避免了加速度突变的现象，但由于本身的算法太过复杂，不利于程序编写。因此，本文采用的是5段S型速度曲线，相对于常规的7段曲线进行了简化，减小了匀加速和匀减速阶段。这样既保留了加速度平稳变化的优势，又在一定程度上减轻了算法编写的工作量[11]。

根据5段S型速度曲线的算法公式，计算出曲柄在各个时间段的角加速度曲线，如图7所示。

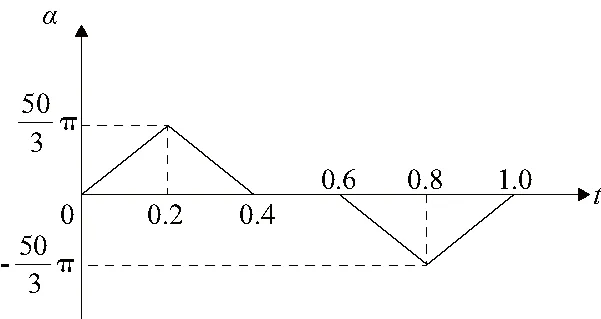
图7 曲柄角加速度曲线示意图

则曲柄的角加速度公式为

(13)

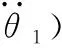
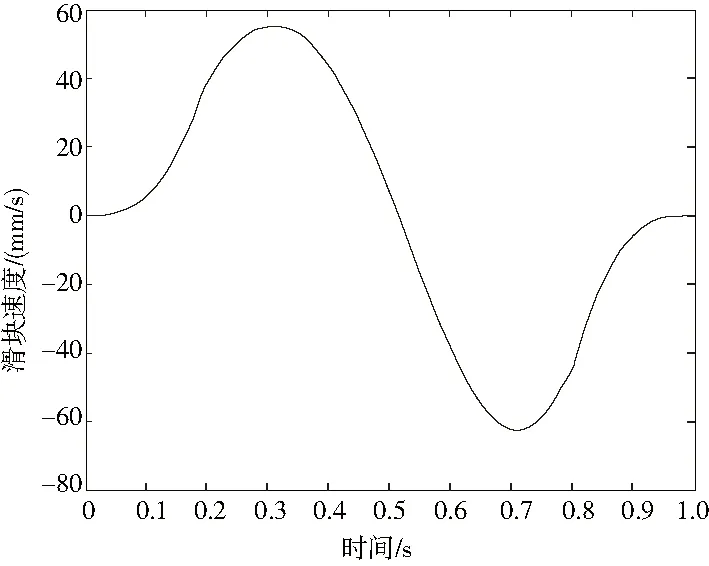
图8 滑块速度曲线示意图

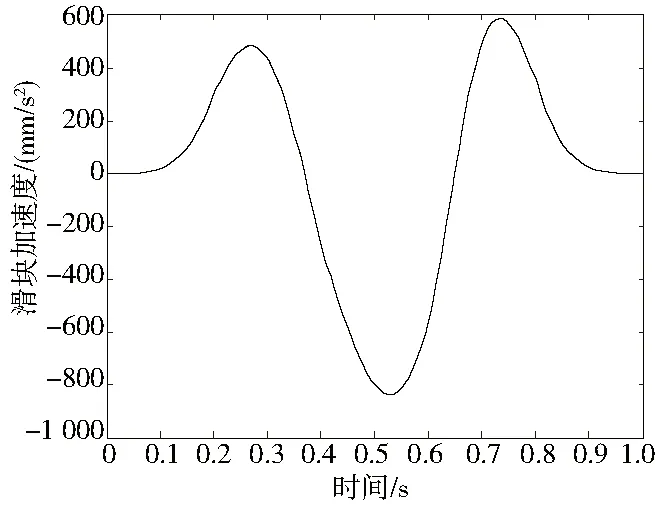
图9 滑块加速度曲线示意图

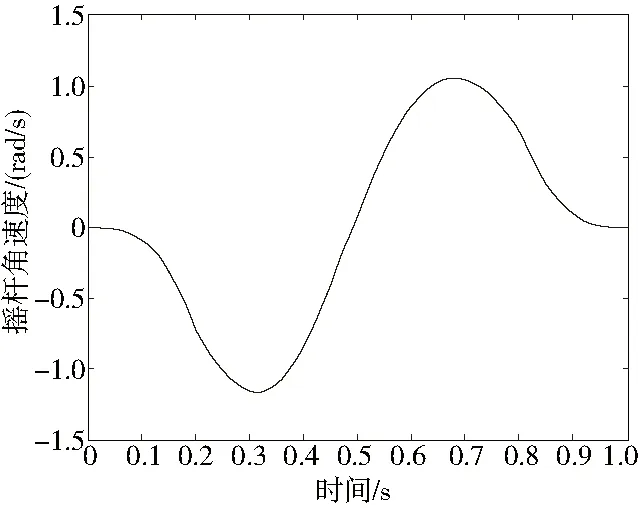
图10 摇杆角速度曲线示意图

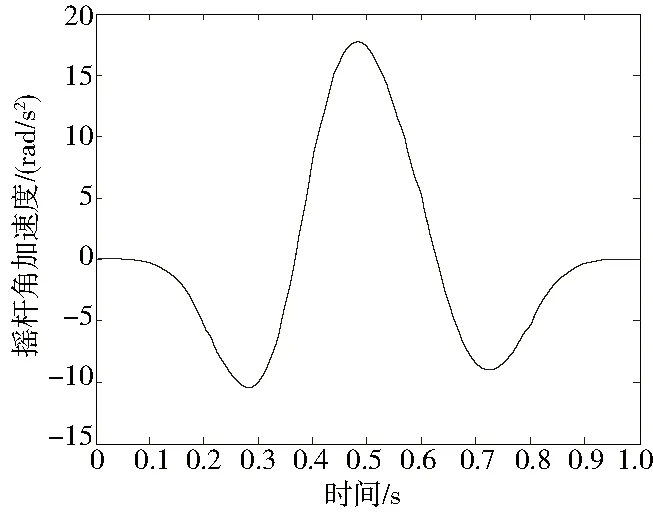
图11 摇杆角加速度曲线示意图

从图中可以看出，滑块与摇杆的速度和加速度曲线变化平稳，没有出现突变的现象，不会对缝合装置产生刚性冲击和柔性冲击。滑块的最大加速度为0.8m/s2，摇杆的最大角加速度为1.2 rad/s2，数值相对较大。为了减小加速度引起的惯性力对勾针运动稳定性的影响，可以通过减轻滑块和摇杆的质量或增大一次缝合的周期来作进一步优化。

3 勾针运行轨迹仿真

3.1 两勾针相对位置分析

在纤维锁扣的过程中，勾针1和勾针2的运动轨迹存在一个交汇点，并且在一个周期内，勾针2的针尖会先后两次处于交汇点位置，如图12(a)中所示。

当第一次到达时，勾针2摆脱了原有线环；在第二次到达时，勾针2需要勾住勾针1上的线环。当勾针2第一次到达交汇点时，为了防止勾针2撞到勾针1上已经勾起的线环，勾针2的针尖应处于勾针1针尖之上，以便提前摆过交汇处。同时，当勾针2向右摆动，第二次到达交汇点时，勾针2的针尖应低于勾针1针尖，以便能够勾住勾针1上的线环。

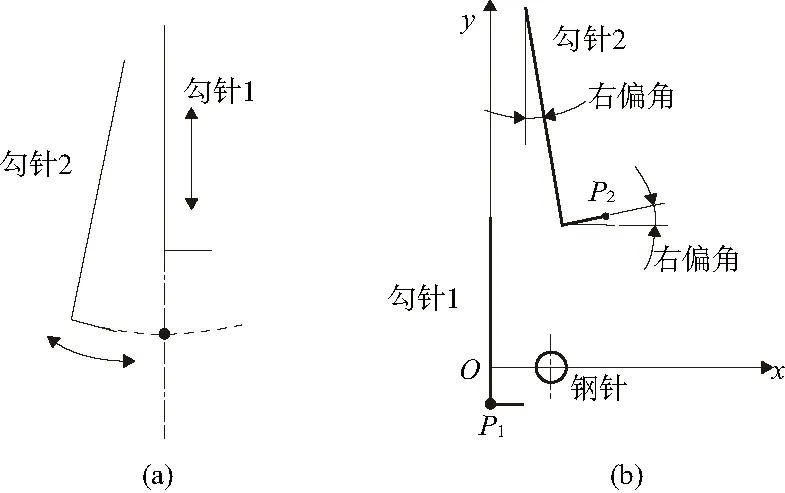
图12 两勾针轨迹示意图

因此，两勾针需要满足以下位置关系：1)初始状态时，勾针1处于下极限位置，勾针2处于右极限位置；2)当勾针2向左摆动，针尖第一次到达交汇点时，勾针2针尖应高于勾针1针尖；3)当勾针2向右摆动，针尖第二次到达交汇点时，勾针2的针尖应低于勾针1针尖。

3.2 模型的建立及仿真

图13表示两勾针的初始状态，此时勾针1在下极限位置，勾针2在右极限位置，以此建立仿真坐标系。以勾针1的运行轨迹为y轴，钢针水平面为x轴，建立平面坐标系。在勾针1和勾针2上分别取特征点P1和P2分析，此时P1点的运动轨迹就是勾针1针尖的轨迹，而P2的运动轨迹就是勾针2针尖的轨迹。则P1与P2的坐标可以表示为：

(14)

式中：数值4为勾针2针尖的长度；s表示装置的安装高度，为60mm；H表示滑块当前所在高度；β表示摇杆当前与机架的夹角(即θ3)；α表示勾针2与摇杆的安装角，为10°。

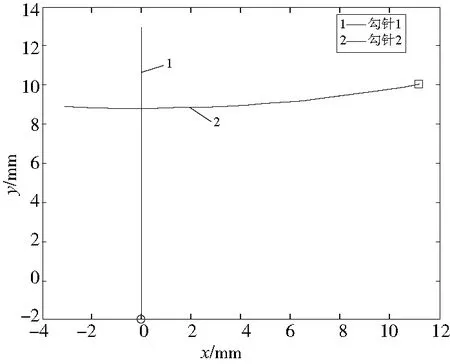
图13 初始状态

将四连杆运动学方程代入P1与P2的坐标表达式中，并利用MATLAB求解出两个点的运动轨迹[13]，如图14、图15所示。

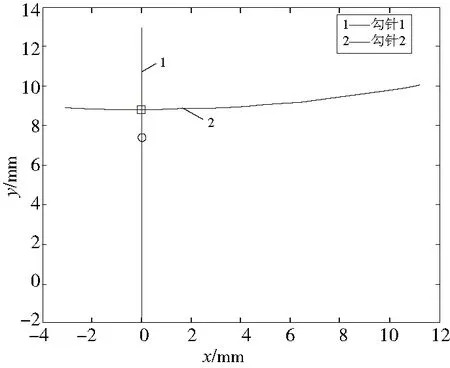
图14 勾针2第一次到达交汇处

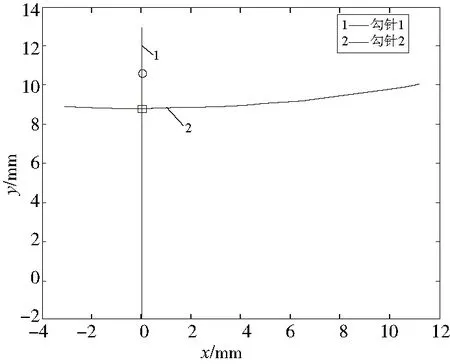
图15 勾针2第二次到达交汇处

图中线1表示勾针1的运行轨迹，线2表示勾针2的运行轨迹。圆圈和方框分别表示P1和P2点当前所在位置。

从轨迹图中可以看出，当勾针2向左摆动，针尖第一次到达交汇处时，勾针1针尖位于勾针2针尖下方约1.8mm；当勾针2越过左极限位置，向右摆动，第二次到达右极限位置时，勾针2针尖位于勾针1针尖下方约2mm处。可知，两个勾针的相对位置关系满足设计要求，利用双勾针实现链式线迹的方案具有可行性。

4 结语

针对立体织物穿刺工艺中采用人工实现纤维锁扣的不足，本文根据传统缝纫机缝合方式，设计了一种基于双四连杆机构的缝合装置，通过两个勾针之间的运动配合实现链式线迹。本文主要的工作和结论为：

1)根据纤维锁扣工艺，确定了勾针的运行轨迹和极限位置，利用解析法求出各杆长度。

2)建立了曲柄滑块机构和曲柄连杆机构的运动学模型，推导出两个勾针的位移、速度和加速度方程。

3)采用5段S型速度曲线模型确定曲柄的运动参数，并利用MATLAB对勾针运动状态进行了仿真，验证了缝合装置能够平稳高效运行。

4)对两勾针的空间位置进行了数学建模和仿真，分析了在3个关键位置时勾针1和勾针2的相对位置关系，验证了两勾针的运动轨迹满足设计要求，证明了该缝合装置具有一定可行性。