基于Ansys Maxwell的电磁式磁滞张力器仿真分析

王庆东，夏港东，秦浩杰，周文聪，张昊

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

在纺织加工过程中，纱线张力是一个十分重要的参数，从纺纱到织造的各个工序，张力的大小和稳定直接关系到产品质量、生产效率以及后续加工的顺利进行[1]。因此，纱线张力器成为控制纱线张力必不可少的装置。

目前市售的纱线张力器以机械式为主，常见的有空气阻尼式以及油阻尼式，如图1所示[2]。相比较而言，传统的机械式纱线张力器往往具有结构简单、维修和操作方便等诸多优点,然而其缺点也尤为明显，如：1)张力控制精度低，一致性差；2)张力器工作过程中始终与纱线产生摩擦，容易损伤纱线；3)自动化程度低，无法由计算机进行控制。

图1 常见纱线张力器

为满足纺织行业不断提高的标准要求，纱线张力器逐渐朝着自动化、智能化方向发展。近年来国外出现了一种高档纺织机械——电磁式磁滞纱线张力器[3-5]。相较于传统机械式张力器而言，该张力器的最大特点是可以通过计算机对纱线张力进行实时的、连续的调节。由于采用计算机进行控制，既可以灵活地对单根纱线的张力进行控制，也可以实现大范围的群控[6]。此外，该张力器还可以连接到非接触式张力监测系统，从而实现对纱线张力的闭环控制，因而具有广阔的应用前景[7]。本文立足于国内外相关理论研究成果，借助有限元分析方法对该类型张力器的特性进行研究，为其日后在国内市场的广泛应用奠定了基础。

1 电磁式磁滞张力器的结构及原理

电磁式磁滞张力器是基于电磁阻尼原理实现对纱线张力控制的[8]，其结构如图2所示。外部静壳体8将整个结构包裹在内，形成封闭的磁回路并同时隔绝外部磁场的干扰。磁芯5由具有高磁导率的软磁材料制成，聚集内部的磁场能量。转轴7在滚珠轴承3的支撑下，一端与抱线轮1固连，另一端通过法兰与转子6连接。励磁线圈4均匀缠绕在线圈架上并将磁芯5包含在内侧。张力器工作时，线圈4通电，抱线轮在纱线的主动牵引下转动。另一端，由磁滞材料制成的转子6作为耗能元件被动旋转，消耗磁场能量，产生阻碍纱线运动的磁滞转矩，使纱线受到张力作用[9]。调整线圈4两端电压的大小即可改变磁滞转矩，实现对纱线张力大小的调节。线圈未通电时，转子在磁芯5间自由旋转，其阻力仅来源于轴承3处的摩擦力。

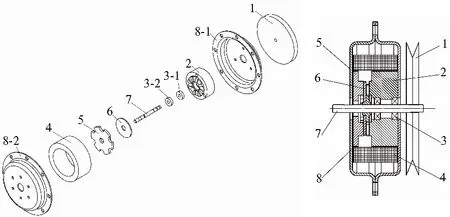
1—抱线轮；2—磁芯①；3—轴承；4—线圈；5—磁芯②；6—转子；7—轴；8—外壳。图2 电磁式磁滞张力器结构图

该张力器的具体性能要求如表1所示。

表1 张力器的性能要求

2 仿真模型的建立

分析电磁场问题时传统的方法是从模型中抽象出一个等效的磁路，再采用解析的方法分析其磁场。由于电磁式磁滞张力器的磁路较为复杂，这使得利用解析法研究其磁场较为困难[10]，而有限元法的广泛应用为解决该类问题提供了极大的便利。本文以课题组研制的一款电磁式磁滞张力器为例，利用Maxwell软件对该张力器进行仿真分析[11]。

由于张力器的结构不具有空间对称性，无法将三维磁场计算问题转化为二维来处理，因而需要建立完整的三维有限元模型[12]。此外，为降低问题分析的复杂性，作出以下假设[13-14]。

1)忽略转子的涡流效应和软磁材料(定子磁芯及外壳)的磁滞损耗；

2)转子的转速保持不变；

3)励磁绕组由空心圆柱体等效替代，绕组内部电流密度分布均匀。

张力器的主要参数如表2所示，相关参数定义如图3所示。定子磁芯及外壳均选择具有高磁导率的电工纯铁DT4，励磁线圈定义为铜材料copper，选择FeCrCo材料作为转子材料并在软件内部将其定义为磁滞型材料。软件内部自带的材料库中并不包含DT4和FeCrCo材料，需要从外界导入两种材料的B-H曲线。由于忽略了涡流效应的影响，两种材料的电导率均设为0。线圈绕组安匝数设为342A，指定求解域属性为空气。在瞬态场分析模块中，还需要额外定义运动区域band，将转子包含在内，并设置其绕z轴转速为1 000r/min。此外，设置仿真时长为20ms，计算步长为0.2ms。

表2 张力器的主要参数

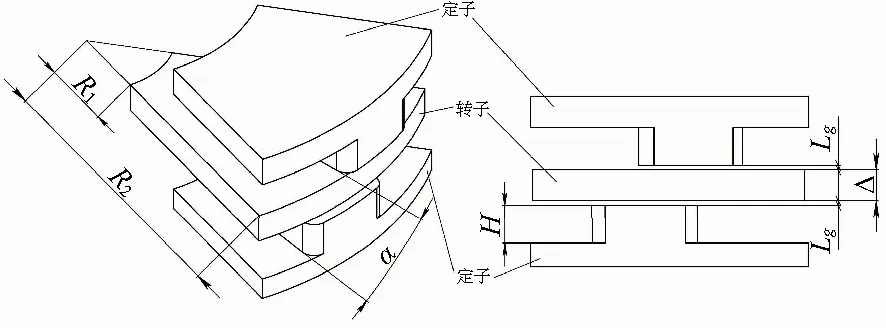
图3 相关参数定义

3 仿真结果

借助Maxwell软件的静态磁场求解器，通过数值计算，得到了张力器内部磁感应强度分布，如图4所示。从图中可以看出，磁力线主要集中在张力器内部的磁性材料上，并依次穿过定子磁极、气隙、转子最终汇聚于张力器外壳，形成一个封闭的内部磁回路。图5为转子表面磁感应强度分布云图。

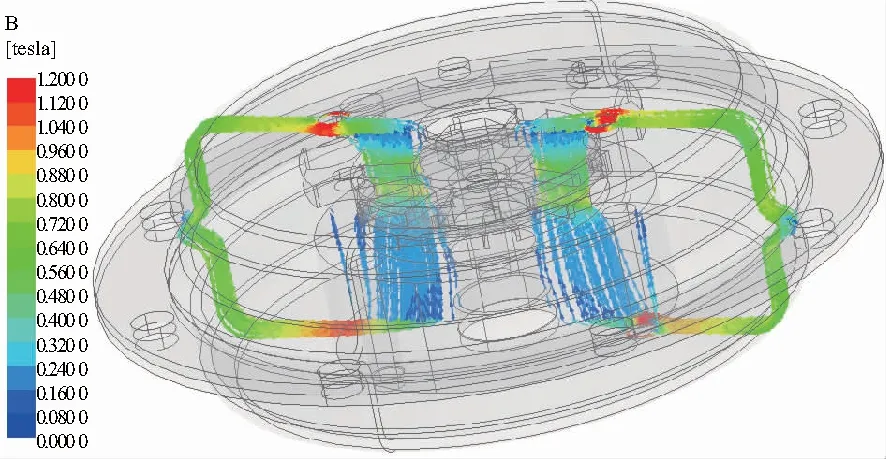
图4 张力器磁感应强度分布及磁力线走向

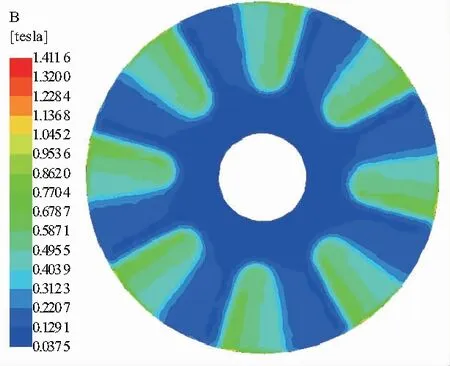
图5 转子表面的磁感应强度分布云图

图6所示为磁滞张力器的转矩输出曲线。从图中可以看出，输出转矩在初始时刻有轻微震动，随着时间的推移，磁滞转矩的数值波动减小，趋于稳定，并最终稳定在32mN·m左右，符合预期要求。

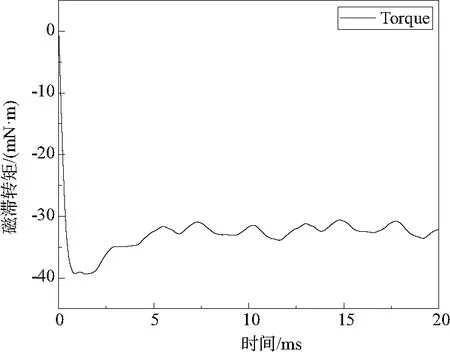
图6 磁滞转矩随时间变化曲线

3.1 气隙对磁滞转矩的影响

保持表1中其他参数不变，仅改变气隙大小，得到图7所示磁滞转矩与气隙的关系曲线。从图中可以看出，随着气隙的增加，磁滞转矩急剧减小。由图2可知，张力器的磁传导回路主要包含定子磁芯、气隙、转子以及外壳。而定、转子以及外壳都是由磁性材料制成的，其相对磁导率要远高于空气磁导率，故而磁场能量主要损失于气隙中。因此，在磁动势大小一定的情况下，磁回路中的气隙越大，其中的磁场能量损失也就越大，转子的磁通密度也必然减小，从而导致磁滞转矩减小。因此，理论上减小气隙可以提高磁滞转矩，但过小的气隙会对机械加工和装配提出更高的精度要求，使得零件的加工难度加大，特别是对转子的加工精度要求更高[15]。故而需要综合考虑各方面因素，选择合适的气隙大小。

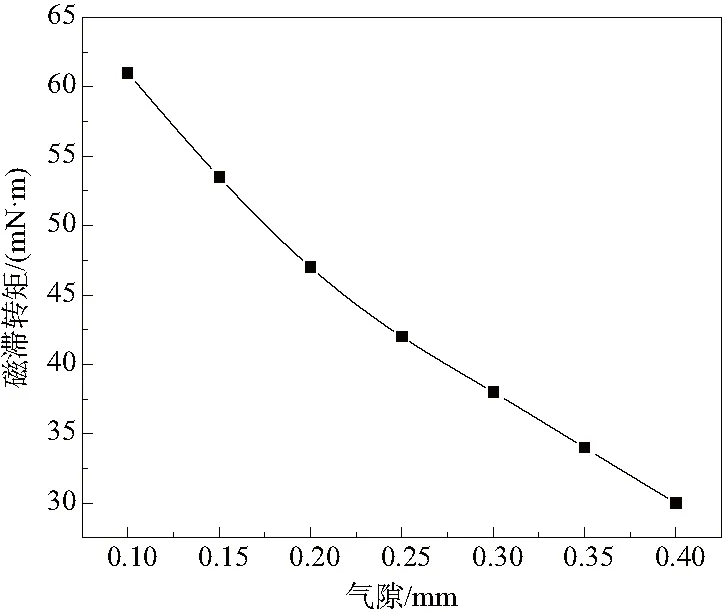
图7 气隙对磁滞转矩的影响

3.2 电流对磁滞转矩的影响

电流的大小是影响电磁式张力器磁滞转矩大小的重要因素。张力器工作时，需要根据实际需要将电流设定在特定的数值。基于表1中的结构参数在不同气隙大小下进行计算，得到了如图8所示的关系曲线图。从图中可以得出，在不同气隙大小下磁滞转矩随电流变化规律基本保持一致。当电流较小时磁滞转矩增加缓慢，而随着电流的不断增加，磁滞转矩显著增大并与电流近似维持着线性关系。当电流超过一定范围后，磁滞转矩的增加幅度趋于平缓，其原因在于随着电流的增加，磁性材料的磁感应强度也趋于饱和，不再随着电流的增大而增大，增加的电流对转矩的影响很小。从图中可以看出，电流在30～70mA范围内，磁滞转矩与电流之间有着良好的线性关系，磁滞转矩可以达到40mN·m，符合设计要求。

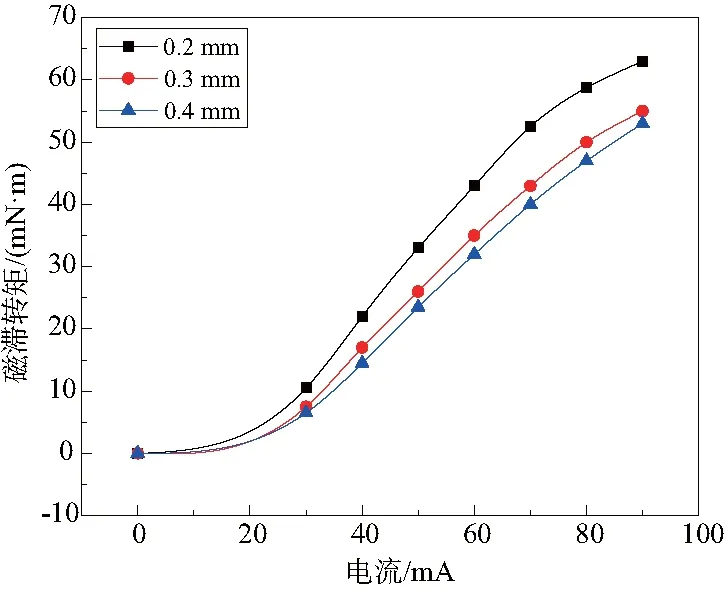
图8 磁滞转矩与电流关系图

3.3 磁极相对角度对磁滞转矩的影响

张力器的定子磁芯由两部分组成，且分别置于转子两侧，如图2所示。两定子磁芯的端面均有若干齿形磁极，张力器装配时，两齿形磁极之间一般错开一定角度，磁极间相对错开角度α定义如图3所示。保持表1其他参数不变，在多组气隙下对张力器在不同磁极相对角度下进行仿真计算，可以得到磁极相对角度与磁滞转矩的关系，如图9所示。

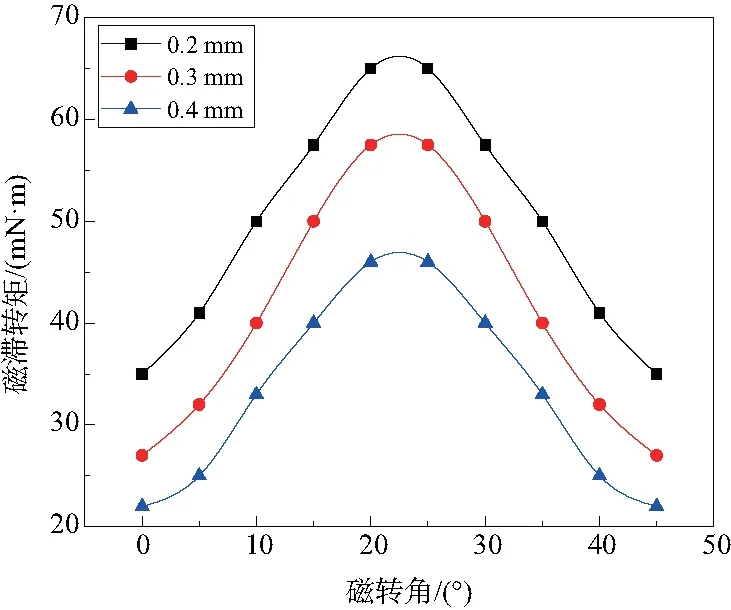
图9 磁极相对角度对磁滞转矩的影响

定子磁极端面的齿形磁极沿周向等距排列，磁极个数为8时，相邻两磁极间的相对角度θ=45°。图9中，在角度α<θ/2时，磁滞转矩随着相对角度的增加而不断增大，而当α>θ/2时，磁滞转矩逐渐减小。在α=45°时，两磁极重合，其磁滞转矩大小与起始位置相等。转子表面的磁密B可以分解成径向Bn和切向Bτ两部分，而Bτ是影响磁滞转矩大小的主要因素。在一定范围内，α增大，切向磁密Bτ也随之增大，而超过一定范围后Bτ反而减小。因此出现了图9所示的关系曲线。

3.4 转子厚度对磁滞转矩的影响

在保证其他参数不变的情况下，随着转子厚度的增加，气隙逐渐减小，这就使得转子磁感应强度增大，磁滞转矩也随之增大，如图10所示。然而，随着转子厚度的不断增大，磁阻和漏磁也在增加，在厚度超过一定范围以后，转子中增加的磁势反而消耗在转子内部的损耗上，对磁滞转矩的影响降低。

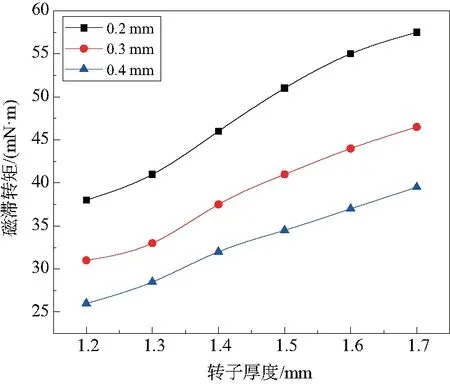
图10 转子厚度对磁滞转矩的影响

3.5 磁极个数对磁滞转矩的影响

改变磁极个数并在多组气隙大小进行数值计算，得到了图11所示的关系曲线。磁极个数较少时，转子的磁通密度低，从而产生的磁滞转矩也较小。随着磁极个数的增加，磁滞转矩迅速增大。然而，磁极个数增加时，各个磁极的漏磁也随之增加，超过一定范围后，磁滞转矩反而随着磁极数目的增加而减小。计算结果表明，在磁极个数为10时磁滞转矩达到最大。

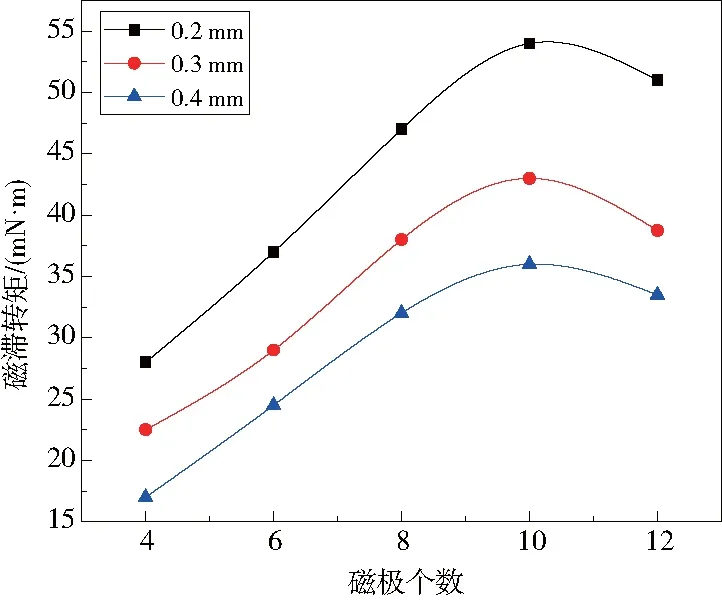
图11 磁极个数对磁滞转矩的影响

4 结语

由以上仿真结果表明：

1)电流是影响磁滞转矩大小的关键因素。磁滞转矩与电流的关系曲线中有一段近似线性的区间，也是张力器的最佳工作区间，且满足在10～30mN·m范围内线性可调的设计要求。

2)气隙大小的选择关系到张力器的最终性能。同时，过小的间隙也会对零部件加工精度和装配提出更高的要求。因此，需要综合考量这两方面的要求，选择大小合适的空气间隙。

3)磁极的相对角度和磁极个数是影响磁滞转矩另一重要因素。计算结果表明，在相对角度α=22.5°、磁极个数p=10时输出转矩接近60mN·m，极大地拓宽了张力器的线性可调范围。

4)转子厚度的增加对磁滞转矩有着明显的影响，但厚度的增加也使得转子的转动惯量增加，因而在设计时需要额外考虑动力学方面的影响。

电磁式张力器是一种精密纱线张力控制器。本文借助Ansys Maxwell软件研究了不同结构参数对张力器性能的影响，证明了通过有限元方法研究该类型张力器的可行性，也为日后的设计制造和升级优化奠定了基础。