翼伞组提带张力传感器的有限元分析

邵天城，郭瑞鹏，李前奇，赵敏，姚敏

(南京航空航天大学 自动化学院，江苏 南京 211106)

0 引言

翼伞飞行方向及下降速度具有可操作性，广泛应用在民用和军用的降落伞空投领域中。翼伞降落的各个阶段，翼伞的形状、组件之间的位置会发生剧烈的变化，承载传力作用的组提带张力也会出现大范围的实时变化。掌握翼伞降落过程中张力的变化对翼伞飞行的安全性以及着陆地点的精确性都至关重要[1]。

随着CAD技术的发展，可以通过计算机进行设计并分析结构特性，在提高设计效率的同时可减少设计成本。本文使用SolidWorks进行传感器结构设计，再导入ANSYS Workbench18.0对装配体进行静力学分析和模态分析，验证传感器结构设计的合理性。

1 传感器结构设计

目前市场上用于组提带张力测量的传感器屈指可数，例如美国 MEAS的EL20-S458和日本KYOWA安全拉力传感器LBT-A-20KNSA1。但这些产品的量程不满足翼伞的最大张力，其次这些产品不适用组提带的宽度，再次就是这些产品是以有线的形式对组提带张力数据进行传输，有线的形式可能会干扰到翼伞的开伞，造成危险。本文根据翼伞组提带的特点，设计了一种测量范围为0～25 000N的无线张力传感器结构，如图1所示。

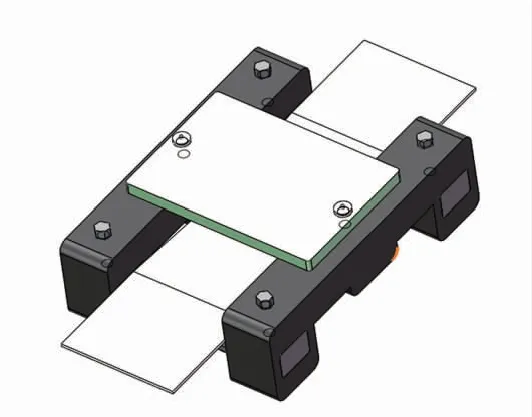
图1 工型张力传感器结构

张力传感器由采集电路PCB板和传感器体两个部分组成。两个部分使用螺丝连接，在连接处加上弹簧防止传感器与PCB板硬接触造成PCB板损坏。采集电路PCB板上装有蓝牙模块，可将采集到的数据发送给伞载系统，实现无线采集功能。弹性体部分非一体化结构，是由工字型主体、插销式力柱、螺丝三部分组成。采取这种工字型对称结构的优势如下：1)在受到组提带张力时，4个悬臂梁所产生的应变是均匀的，可保证传感器线性度；2)组提带在空中拉直瞬间将力传导至传感器后，力柱会产生微弱的变形使得组提带滑动。本设计的对称式结构使得传感器的中心落在中间力柱的中点处，减少组提带滑动的可能性以提高组提带和力柱的贴合度，保证测量的准确性。

2 装配体静力学分析

用于传感器的材料通常应能承受较大的冲击力，这样不易损坏传感器设备。同时材料应有良好的耐疲劳性，可以有效保证传感器的使用寿命。综合考虑各种材料参数对传感器测量的影响，选用40CrNiMo作为传感器的结构材料[3]。该材料具有高弹性极限和弹性模量，常用在各种大量程力学传感器上。材料的泊松比为0.3，弹性模量为210GPa，屈服强度为850MPa。

静力学分析最关键的步骤取决于正确的施加载荷与约束，因此需准确建立力学结构模型。传感器的纵切面如图2所示，组提带与3根力柱的上表面接触，当组提带紧绷时对3根力柱产生作用时，使得两侧的悬臂梁发生向上的弹性形变。

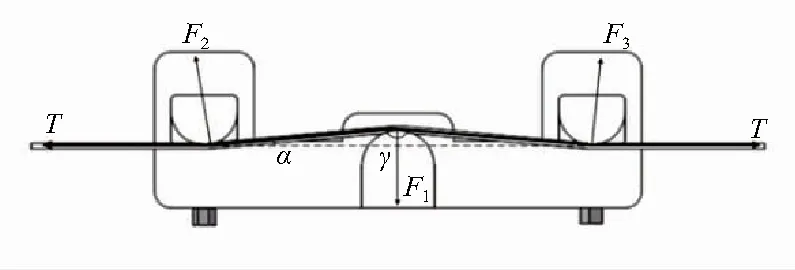
图2 传感器受力模型

可以得到施加在3根力柱上力的具体数学表达式如下：

F1=2Tsinα

(1)

(2)

夹角α影响着整个传感器的性能。夹角α越大，施加在力柱上的等效力就越大，传感器的灵敏度越大；但是若夹角α选得过大，传感器的量程会缩小，甚至可能会发生传感器两侧悬臂梁断裂的危险事件。出于对传感器的灵敏度、量程、结构大小和安全4个方面考虑，夹角α选择6°较为合适。根据式(1)和式(2)只需得出F1、F2和F3就可以对传感器施加载荷。

传感器测量是基于弹性体随着力的大小发生相对应的线性弹性形变，因此只有在传感器不发生塑性形变的范围内，测量才有效准确。当张力达到最大时，在两侧力柱上施加轴承载荷，中间力柱施加远端位移约束后进行静力学分析，得到的应力分布如图3和图4所示。由图3可看到最大的应力集中分布在主力臂的弯折零星红色部分处，传感器最大的应力为828.93 MPa，小于合金钢40CrNiMo的最大屈服强度850 MPa，理论上此材料能够满足张力测量范围。从图4可见传感器应力较大部分的应力为460 MPa，集中分布在主力梁两侧的绿色区域。应力越大随之带来的应变也就越大，将应变片粘贴在此区域处最为恰当(本刊为黑白印刷，相关疑问可咨询作者)。

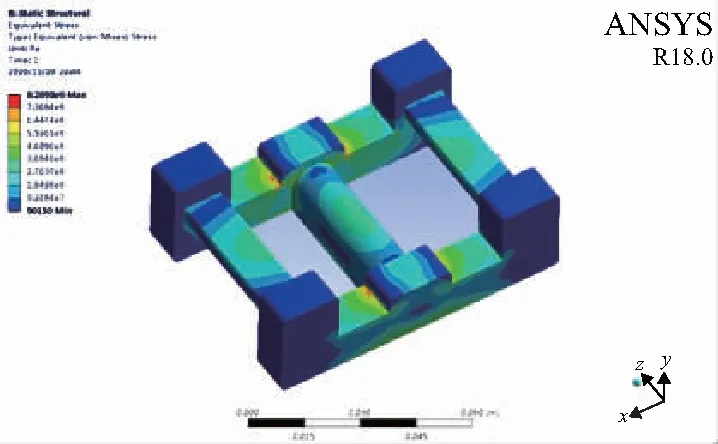
图3 弹性体等效应力分布图Ⅰ

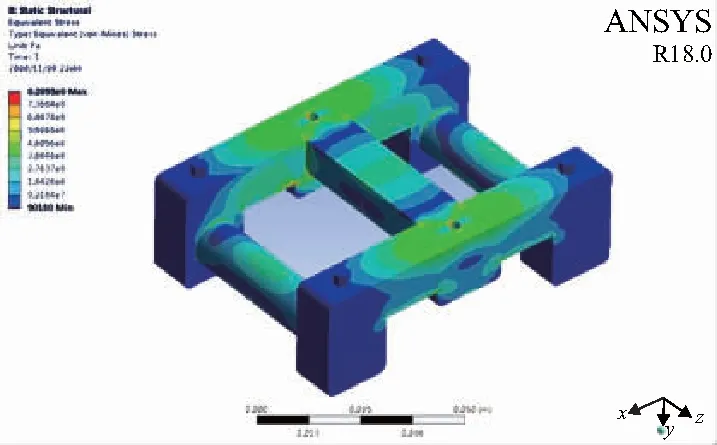
图4 弹性体等效应力分布图Ⅱ

由于所设计的传感器具备对称性，只需将应变片粘贴在传感器上半部分，呈“L”字型构成一个全桥工作电桥，应变片粘贴位置如图5所示。

图5 弹性体应变片粘贴位置图

采用全桥电路有两种优势，一是可以消除应变片敏感栅圆角部分引发的横向效应误差；二是因为张力传感器所在的海拔高度会随着翼伞而发生改变，相应的温度引发额外电阻变化从理论上分析与弹性体应变改变阻值的变化几乎在同一数量级上，所以这种垂直贴法可以很好地对温度进行补偿，提高传感器的测量精度[4-5]。

由于应变片贴在悬臂梁的表面测量其横向的应变，由胡克定律[6]可知，表面应变是正向应变带来的，因此可利用Workbench中的Normal Elastic Strain检测正向应力作用在悬臂梁表面引起x轴的应变，如图6所示。

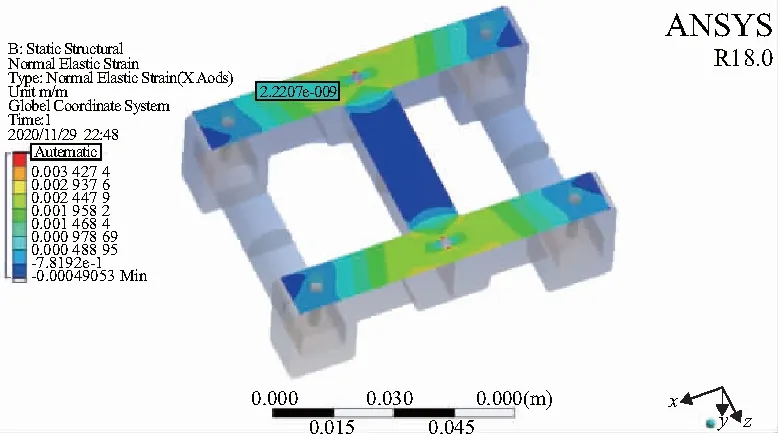
图6 悬臂梁表面x轴的应变图

利用Workbench中的指针探测功能(Probe)对所贴应变片横向测力的部分进行应变采集。应变采集的组数按照2 500N的间隔测量10组数据，每组在应变片的粘贴处采集20次，取平均作为一组值，将张力值与横向应变进行曲线拟合结果如图7所示，可以看到两者呈线性关系。理论上可以验证在此位置上应变片随着张力的改变线性度良好。

图7 张力与应变片横向应变拟合图

3 装配体模态分析

模态分析的目的是确定自然频率、振型和振型的参与系数(即在指定的方向上某个振型参与多大程度的振动)。进行翼伞降落试验的时候，组提带会与张力传感器产生相对移动，传感器受到组提带上张力的冲力会产生振动，若两者发生共振可能会给传感器带来不可恢复性损伤，极大降低传感器的耐用性。为此需对传感器的结构进行模态分析，确定设计结构的固有频率，张力传感器的前三阶振型如图8所示。

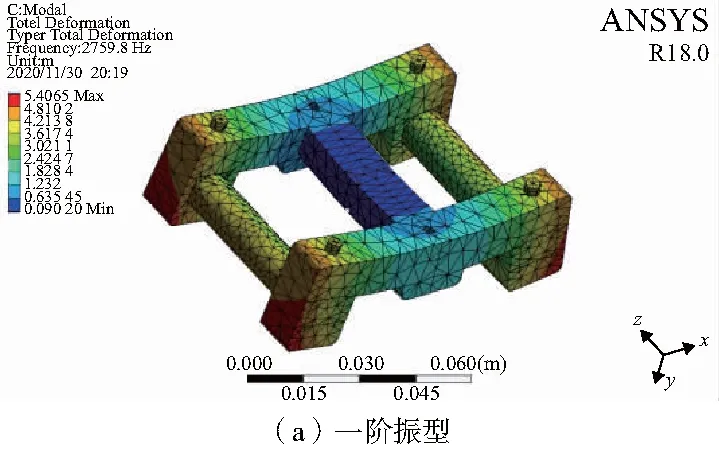
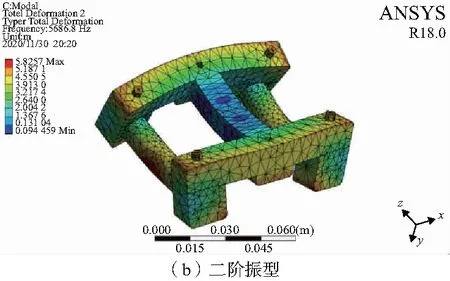
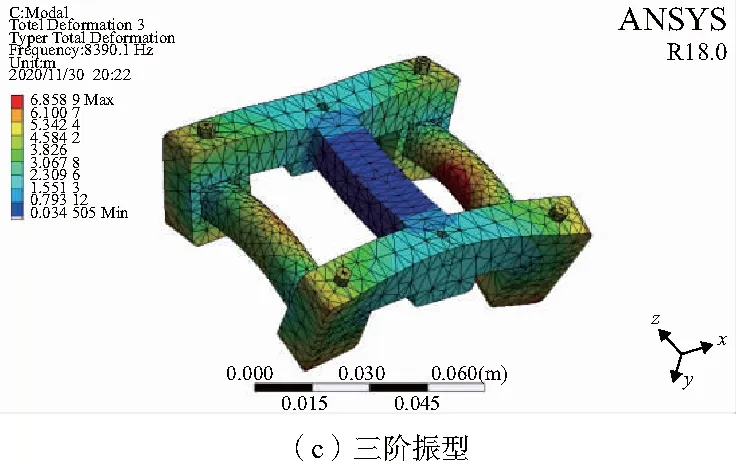
图8 张力传感器的前三阶振型

从仿真结果分析可得，一阶的频率为2 759.8Hz，传感器两侧绕着主力臂在xy平面上振动；二阶的频率为5 686.8Hz，传感器上下两侧向力臂的中点处前后挤压；三阶的频率为8 930.1Hz，传感器两侧绕着主力臂在xy平面上振动；传感器两侧绕着主力臂在xy平面和zy平面上扭转摆动。当阶数增加，传感器的固有频率会越高，振动会越剧烈。由于和张力传感器接触的组提带是由纤维织物组成的，工作频率达不到1 000Hz，因此可以保证两者不发生共振，所设计的传感器不会发生损坏，且能够保持测量的稳定性。

4 结语

1)本文设计了一种适用于翼伞组提带张力测量的无线传感器，其设计结构具有高度的对称性，能够有效保证传感器测量的稳定性和准确度。

2)对张力传感器装配体进行静力学分析，结果表明：应力集中分布在主力臂的弯折处，材料处在弹性变形未产生塑性形变，满足设计要求。在应力较大的主力梁两侧粘贴应变片，分析得到该位置的线性度良好；采用垂直粘贴法的全桥电路，可减小或克服传感器工作状态改变带来的误差。

3)对张力传感器进行模态分析，得到其固有频率和振型。组提带工作频率距离其工作频率较远，组提带不会引起传感器共振，传感器能够稳定地工作。