改进的快速非支配排序遗传算法II及其在投资组合中的应用

胡博, 肖辉, 金浩, 汪镭

(1.同济大学， 电子与信息工程学院， 上海 201804; 2.上海财经大学， 统计与管理学院， 上海 200433)

0 引言

在过去十几年，进化计算领域[1-2]已经对多目标优化问题(Multi-objective Optimization Problems, MOPs)进行深入的研究，并提出了许多有效的算法[3]，如快速非支配排序遗传算法II(NSGA-II)[4]。NSGA-II虽然在多目标优化问题上表现出良好性能，但是其采用的多样性选择机制和快速非支配排序策略[4]仍有不少缺陷。针对锦标赛策略存在重复选择交叉个体的问题，张茂清等[5]引入Levy分布策略和三交叉个体策略以强化后代个体多样性。同样针对此问题，汪镭等[6]提出引入多个交叉父代以降低重复选择父代的概率。进一步，张茂清等[7]又提出在待交叉父代个体每个维度上引入扰动参数改变其值,然后将扰动父代做正常交叉操作产生新后代,以此避免了后代重复个体产生。

为进一步优化NSGA-II性能，本文重新设计了多样性评价机制，并进一步将其引入NSGA-II。通过现有测试函数和一个实际投资组合优化问题综合测试，所提的改进NSGA-II算法(Improved Fast Non-dominated Sorting Genetic Algorithm II, INSGA-II)具有良好的综合性能。

1 基本NSGA-II分析及其改进

NSGA-II主要过程如下：首先初始化种群P，然后执行快速非支配排序和拥挤度距离计算操作；在此基础上，采用锦标赛策略构建交叉池，然后执行交叉和变异操作，并得到子代种群Q；合并父代种群P和子代种群Q, 再次执行快速非支配排序和拥挤度距离计算；根据每个个体所在不同前沿面等级和拥挤度距离选择较优个体保留为子代种群。若满足结束条件，则输出当前种群; 否则进入下次循环。

NSGA-II采用的拥挤度距离可表示如下：

(1)

其中，di表示第i个体拥挤度距离，fk(i+1)表示第i+1个个体第k个目标函数，M表示目标函数总数。

如图1所示，在二维目标空间有A,B,C,D,E和F6个个体。根据拥挤度距离计算式(1)，个体B的拥挤度为4，个体E的拥挤度同样为4。根据直观理解，个体B和E具有相同拥挤度距离，但是很明显个体B比个体E更加拥挤，因为个体B更加靠近C, 而个体E则居于中间位置。因此，基于以上分析，本文提出以下改进计算方式：

图1 拥挤度距离示意图

(fk(i)-fk(i-1)-lenk)2

(2)

其中

(3)

根据式(2)，B拥挤度为0.5，个体E拥挤度为0，说明个体E距离其相邻个体更加均匀。因此，上述改进公式可以在一定程度上弥补原拥挤度评价机制的不足。基于式(2),INSGA-II伪代码可表述如下。

INSGA-II伪代码输入:N(种群大小)输出:P(种群)1:根据种群规模初始化种群P并计算适应值2:执行快速非支配排序和拥挤度距离操作3:While(是否满足结束条件)4: 采用锦标赛策略构建交叉池5: 个体间执行交叉和变异操作6: 合并父代种群P和子代种群Q7: 执行快速非支配排序和改进拥挤度距离(式2)操作8: 更新种群9:End

2 实验及分析

2.1 在测试集上的实验

本文采用ZDT[4]作为测试函数。对比算法为NSGA-IISDR[8], NSGA-II, MOPSO[9]和SPEA2[4]，对应参数按照开发者建议设置。评价指标为HV和IGD[8]。算法最大评价次数10 000次，每个算法运行20次。采用Friedman检验统计算法在不同指标上性能。

表1列出了对比算法在HV指标上实验结果。从表1中可以看出，INSGA-II在除在ZDT3上均取得较好性能。从最后一行统计结果看出，INSGA-II仍然明显超过其他算法。表2列出了对比算法在IGD指标上实验结果。从对比结果可以看出，INSGA-II在6个测试函数上均为最优。从统计结果可看出，INSGA-II性能明显超过其他对比算法。从表1和表2实验结果和统计数据上可看出，本文所提策略确实提高了NSGA-II整体性能。

表1 对比算法在HV指标上实验结果

表2 对比算法在IGD指标上实验结果

图2和图3分别显示了IGD和HV指标的动态变化过程。从图2可看出，INSGA-II收敛速度明显优于其他对比算法；在HV指标上，INSGA-II收剑速度也较为明显，超过了标准NSGA-II 以及其他算法，说明INSGA-II整体性能出众。

图2 算法在IGD指标上的动态数据比较

图3 算法在HV指标上的动态数据比较

2.2 INSGA-II在投资组合优化上的应用

在人们投资过程中，经常需要最大化期望收益以及最小化风险[10]，具体可表达如下：

(4)

其中，x表示决策矢量，对应每一维度表示每支基金回报率，σi,j表示第i支基金和第j支基金协方差，ri表示第i支基金回报率。第一个目标表示整体投资组合风险，第二个目标表示期望回报率。下列仿真采用的数据集为公开数据集 (https://www.metatrader5.com/cn)。

图4展示不同算法所求帕尔托前沿面。如图4所示，INSGA-II所求前沿面的收敛性更加出众，同时可以看出SPEA2优于NSGA-II, MOPSO和NSGA-IISDR。从图5中不同算法在HV指标上的收敛性曲线可看出， INSGA-II收敛速度明显优于NSGA-II, NSGA-IISDR和SPEA2, MOPSO展现出最差收敛速度和收敛性。基于以上分析，可看出INSGA-II综合性能表现较为突出。

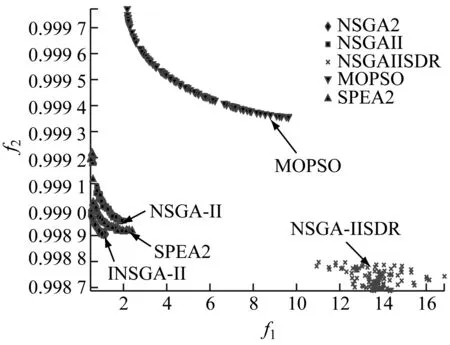
图4 所求前沿面比较

图5 算法在HV指标上的动态展示

3 总结

本文针对经典优化器NSGA-II中拥挤度距离机制无法有效区分较为拥挤个体的缺陷，提出了改进拥挤度评价机制, 并进一步提出了改进的INSGA-II。在ZDT测试集和投资组合优化问题上实验结果和分析表明所提算法的整体性能有了较大的提升。未来的研究工作，应进一步优化投资组合数学模型，以提升该模型在实际应用中的实用性和有效性。