二进制特征图像算法性能分析
刘 高,左小清
(1.昆明理工大学国土资源工程学院,云南 昆明 650093;2.广东省科学院 智能制造研究所,广东 广州 510070)
0 引言
图像特征点提取与匹配是机器视觉的重要组成部分,它在目标识别、视觉导航、图像检索、图像拼接和三维重建等方面发挥着重要作用。选用不同的特征提取算法将导致算法鲁棒性降低,使应用效果受到一定程度影响。故对特征提取算法进行比较,分析其性能具有重要意义。
本文对SIFT、SURF、ORB、BRISK 四种常用的二进制特征算法进行比较,采用指标为算法耗时和特征匹配数目,通过对比实验分析4 种算法在实时性及复杂环境下的鲁棒性。
1 相关研究
特征提取算法研究较多,如Lowe[1]提出的SIFT 算法,由于SIFT 算法计算量很大,后续又有很多改进算法被提出,其中应用最广泛的是Bay 等[2]提出的SURF 算法,Leutenegger 等[3]提出的BRISK 算法,Rublee 等[4]提出的ORB 算法,Alahi 等[5]提出的FREAK 算法等,这些算法具有尺度不变性、旋转不变性、对噪声的鲁棒性等;顾煜洁[6]在SURF基础上引入信息熵和网格划分思想,大大减少了特征提取量;丁国绅等[7]提出一种基于高光谱图像的改进SIFT 算法,提升了算法匹配性能;赵腾飞等[8]在SURF 基础上增加了边缘检测算法,得到图像边缘信息后进行形态学处理,获得较多特征明显的信息;针对ORB 算法在复杂光照环境下匹配精确率较低的问题,袁小平等[9]提出一种基于改进FAST 检测的ORB 算法,提高了复杂光照环境下的鲁棒性;冯宇等[10]通过对SUSAN、Harris、Moraves 等算子性能进行比较,发现Moravec 算子最为简单,但特征点提取质量和抗噪能力表现较差;在图像匹配中,邵进达等[11]提出一种将几何代数法与SIFT 结合的图像匹配算法,可准确定位更多特征点,提高图像对准速度;黄云彬等[12]通过引入对角降维与角度删减方法,分别对SURF 算法中特征点描述子通过降维和误匹配点剔除的方法提升匹配速度和精确度。上述是近年主流的二进制图像特征算法及在此基础上对其进行一定性能提升研究工作的介绍。为了对图像特征算法获得更深入了解,本文选取ORB、SURF、SIFT、BRISK四种主流特征算法,横向对比各算法在鲁棒性和实时性方面的差异,为图像特征研究提供参考。
2 算法基本原理
2.1 SIFT 算法
SIFT 特征提取算法是公认的标准的具有尺度及旋转不变性的斑点特征提取算法,具有良好的旋转不变性、视角不变性、仿射不变性及光照不变性[13]。算法流程如下:①尺度空间和极值点检测;②关键点定位;③特征方向指定。
2.1.1 尺度空间和极值点检测
尺度空间理论目的是模拟图像数据的尺度特征。二维图像的尺度空间定义为:L(x,y,σ) = G(x,y,σ)*I(x,y),其中G(x,y,σ)是尺度可变高斯函数,σ为尺度信息,决定图像的平滑程度,构造高斯差分尺度空间。

为获取尺度空间的极值点,将采样点和与之相邻的所有点进行比较,获取其图像域和尺度域与相邻点对比的大小情况。
2.1.2 关键点定位
为获取关键点位置信息和精度信息,并且剔除低对比度的关键点和不稳定的边缘点,将三维二次函数进行拟合,从而提高其匹配能力和抗噪声性能。
2.1.3 特征方向指定
关键点的方向信息为:
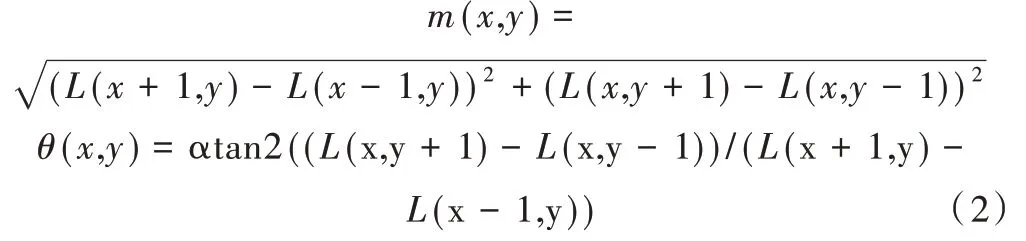
m(x,y),θ(x,y)分别为(x,y)位置处的梯度模值和方向。至此,关键点的位置信息、尺度信息和方向等信息都已得到。
2.2 SURF 算法
SURF 算法的基本原理分为以下几个步骤:
2.2.1 图像积分
SURF 算法采用方块滤波器方式获得像素点的Hessian矩阵行列式,计算积分图像,从而得到SURF 的尺度金字塔。通过原图像获得积分图像中每一个像素点元素的数值,其值为
2.2.2 尺度空间构造
对DOH 近似进行特征点检测,获得二阶微分Hessian矩阵——(fx,y)。通过并行运算对皮拉米德图像中的每一层进行处理,从而构建出高斯金字塔。
2.2.3 特征点位置
如图1所示,对图中的像素点进行处理,通过与相邻像素点进行比较和滤波的方法删除错误特征点,从而获取相应的特征点。

Fig.1 Location of feature points图1 特征点确定
2.2.4 特征点主方向选择
采用Harr 小波,在60°的水平和垂直两个方向上通过0.2rad 的扇形进行间隔旋转,在此区域内再次计算特征,值最大的扇形方向即为该特征点的主方向。
2.2.5 特征描述子生成
选取特征点范围内一个4×4 的区域,得到一个64 维的向量描述子,这4 个方向特征值依次是垂直方向值、水平方向值、垂直方向绝对值和水平方向绝对值。
2.3 ORB 算法
ORB 算法是FAST特征点检测[14]和BRIEF 特征描述子[15]的结合与改进。ORB 算法分为FAST 特征点检测、BRIEF 特征描述两个步骤。
2.3.1 FAST 特征点检测
设定需提取的特征点数为N,并将FAST 的阈值降低,FAST 特征点数目大于N。在特征点处计算Harris 的响应值,取N 个响应值大的点作为检测到的特征点,再计算特征点主方向:

其中,C 为质心位置,θ 值为FAST 特征点的主方向。
2.3.2 BRIEF 特征描述
特征点获取后,采用BRIEF 特征描述。BRIEF 算法的核心思想是以特征点为中心,取S×S 的邻域窗口。在窗口内随机选取点对,将选取点对的像素进行大小比较并执行二进制赋值,最后重复随机选取N 对进行二进制赋值操作,即可完成BRIEF 特征描述。
2.4 BRISK 算法
BRISK 算法特点是能够大幅降低计算成本,提高特征检测速度。BRISK 算法包括尺度空间特征点检测、特征描述子的构建、特征匹配3 个步骤。
2.4.1 尺度空间特征点检测
在BRISK 的特征检测框架结构中,BRISK 算法构建了由4 个内层和4 个中间层组成的尺度空间金字塔,并采用AGAST 算法[16]进行特征点检测。
2.4.2 特征描述子构建
BRISK 算法通过像素灰度值大小的比较,得到一个二进制向量来描述特征点。BRISK 采用了邻域采样模式,即以特征点为圆心构建多个不同半径的离散化同心圆,然后在每一个同心圆上获得具有相同间距的N 个采样点,如图2 所示。

Fig.2 Sampling mode of BRISK图2 BRISK 的采样模式
首先对图像进行高斯平滑处理从而消除图像灰度混叠的影响,通过计算特征点的特征模式方向,将采样模式围绕特征点旋转为arctan2(gy,gx)的角度,使得特征描述子具有旋转不变性,将全部特征点进行像素灰度值比较得到512bit 的二进制字符串描述子。
2.4.3 特征匹配
BRISK 算法采用二进制描述子,故可采用汉明距离评定特征描述子之间的匹配程度,通过汉明距离的大小来判断是否匹配成功。
3 算法实时性及鲁棒性分析
对几种图像特征提取算法进行比较分析时应考虑数据集的客观性和合理性,评价指标的逻辑性和评价角度的实用性。本文选取ORB、SURF、SIFT、BRISK 四种主流特征提取算法,评价指标为运行时间及特征匹配对数[17],衡量算法的实时性及在发生旋转变换、模糊变换、光照变换、视角变换场景下的鲁棒性。
3.1 算法匹配速度分析
评价算法性能的一个重要指标是运行时间。选用真实环境和Euroc 数据集中正常场景下相机有一定偏移量的图像对进行实验,使用OpenCV 提供的特征提取算法的调用接口设置默认参数。为保证条件一致,将图片格式统一。将真实环境和数据集环境下的相片统一调整为512×512 像素,并在实验时调整为灰度图像。为降低特征提取后误匹配的比例,通过RANSAC 算法[18]剔除图像误匹配对。
图3 和图4 分别为ORB、SURF、SIFT、BRISK 四种算法在EuRoC 数据集和实验环境正常场景中的特征提取及匹配结果,从中可得出结论:4 种算法提取的特征在图像中分布比较均匀,ORB、SIFT、SURF 三种算法提取及匹配的特征数量较多,BRISK 提取及匹配的特征数量较少。如表1 所示,对运行时间与匹配对数进行分析,在达到足够的匹配数前提下,ORB 算法最多需要24.6ms 即可完成图像对的匹配,速度最快,可满足实时性需求,执行速度排序为ORB>BRISK>SURF>SIFT。

Fig.3 Feature detection and matching of ORB,SIFT,SURF and BRISK in normal environment图3 正常环境下ORB、SIFT、SURF、BRISK 特征提取及匹配

Fig.4 Feature detection and matching of ORB,SIFT,SURF and BRISK in real environment图4 真实环境下ORB、SIFT、SURF、BRISK 特征提取及匹配

Table 1 Matching number and running time(ms)of feature detection algorithm while matching the same images表1 各特征提取算法匹配相同图像的匹配数目和运行时间(ms)
3.2 旋转变换鲁棒性分析
当图像有一定旋转量时,像素点会以旋转中心为圆心进行相应角度旋转,特征点的邻域信息将相应发生变化。为探讨4 种算法在旋转变换中的鲁棒性,对相同图像执行旋转操作,逐次提高旋转角,并将图像与原始图像依次匹配,通过观察特征正确匹配数的变化分析算法对旋转变换的鲁棒性。在此选用Mikolajczyk 数据集中的bark 图集进行测试。
结合表2 和图5(彩图扫OSID 码可见,下同)可以发现,当图像具有一定的旋转角度时,特征匹配对的数量会减少较多;当旋转角度较小时,SIFT 和BRISK 算法可以表现出一定的稳定性;当旋转角度较大时,ORB 和BRISK 算法失效。

Table 2 Matching number of each feature detection algorithm while matching rotated images表2 各特征提取算法匹配旋转变换图像的匹配对数

Fig.5 Line chart of matching number while images are rotated图5 图像旋转时匹配对数折线
3.3 模糊变换鲁棒性分析
图像模糊程度增加会导致图像的分辨率和识别能力下降。为研究该算法在模糊情况下的鲁棒性,对同一图像进行不同的高斯核处理。将处理后的图像与原始图像相匹配,通过观察匹配对数的变化研究该算法对模糊变换的鲁棒性。在此使用mikolajczyk 数据集的bikes图集进行测试。
结合表3 和图6 可以看出,当模糊程度逐渐增加时,各算法的匹配对数相应减少,SURF 和ORB 算法稳定性稍好;当模糊程度增大时,能够获取到足够的特征匹配数,BRISK和SIFT 算法在模糊变换方面的鲁棒性较差。

Table 3 Matching number of each feature detection algorithm while matching blurred images表3 各特征提取算法匹配模糊变换图像的匹配对数

Fig.6 Line chart of matching number while images are blurred图6 图像模糊时匹配对数折线
3.4 光照变换鲁棒性分析
不同的光照条件会使图像中的某些特征更加突出,同时由于阴影和遮挡的影响,一些特征会被削弱,导致图像的特征点位于不同的灰度空间中,增加了特征匹配的难度。为探究发生模糊变换时算法性能,选取相片须对同一图像亮度进行调整,将调整亮度后的图像与原始图像进行匹配,通过观察特征匹配对数的变化分析算法对光照变换的鲁棒性。在此选用Mikolajczyk 数据集中的leuven 图集进行测试。
通过表4 和图7 可以看出,当光照下降不大时,4 种算法稳定性都比较好,图像光照继续降低后都能够获取到足够量的匹配数,但BRISK、ORB 算法表现出了更强的稳定性。

Table 4 Matching number of each feature detection algorithm by different lighting effect表4 各特征提取算法匹配光照变化图像的匹配对数
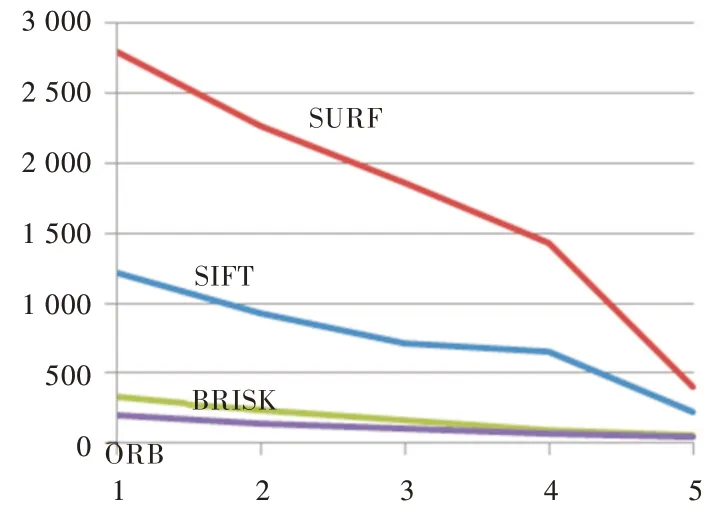
Fig.7 Line chart of matching number while light of images is effected图7 图像光照变化时匹配对数折线
3.5 视角变换鲁棒性分析
当图像发生视角变换时,会使得原始图像中部分特征点落在靠近图像物体处或超出图像范围,视角变换角度越大,保留的特征点就越少。为探究在视角变换场景下的算法性能,对原场景旋转一定角度进行拍摄,将不同视角的相片与原始相片进行匹配,通过观察特征匹配对数的变化分析算法对视角变换的鲁棒性。在此选用Mikolajczyk 数据集中的graf 图集进行测试。
结合表5 和图8 可以发现,当视角角度变换时,4 种算法匹配数目都急剧下降,但变换角度比较大时,SIFT 和SURF 算法依然有足够的特征匹配数,且SURF 算法的鲁棒性更强。

Table 5 Matching number of each feature detection algorithm by the changed perspective表5 各特征提取算法匹配视角变换图像的匹配对数

Fig.8 Line chart of matching number when perspective is effected图8 图像视角变换时匹配对数折线
4 结语
图像特征提取算法的实时性以及在复杂场景中表现出的鲁棒性是图像特征研究的重要内容,本文选取ORB、SURF、SIFT 和BRISK 四种主流特征提取算法,在分析这几种算法原理及特点基础上,探究了算法的运行速度和复杂环境下鲁棒性对比。实验结果表明,在实时性方面,ORB算法有很大优势,具备良好的实时性,且ORB 算法在光照变化的情况下表现出较好的稳定性;SURF 在模糊变换、光照变换、视角变换场景下,能够获取较多的特征匹配数,鲁棒性最强,有利于后续工作展开,在不考虑时间消耗情况下,SURF 可作为首选算法;BRISK 算法在光照变化情况下具有较好的稳定性。本文结果可为后续图像特征研究工作提供参考。设计更合理的评价参数对图像特征相关算法进行比较分析是下一步研究方向。

